新能源汇集系统短路故障清除后的暂态过电压机理

于思奇，孙大卫，吴林林，李蕴红，王 潇，邓晓洋，宋嘉炜

（国网冀北电力科学研究院（华北电力科学研究院有限责任公司），北京 100045）

0 引言

风电、光伏等新能源汇集系统经超／特高压交流输电通道送至主网已成为新能源电力系统发展的重要特征之一［1］，新能源汇集系统呈现出比传统电网更复杂的稳定特征［2］。新能源汇集系统与主网间的电气距离一般较远且同步电源容量有限［3］，这使得系统在部分扰动后易产生较为严重的暂态过电压问题［4］。已有多篇文献［5-6］报道，发生交流故障后新能源汇集系统存在过电压导致的新能源机组连锁脱网或设备损坏风险。华北地区作为我国千万千瓦级新能源基地的代表，张家口、承德等地已形成了以新能源为主体的电网形态。基于电网调度部门在新能源汇集系统的现场故障录波数据发现，短路故障清除后的暂态过电压瞬时值峰值远超过我国国家标准中要求的新能源高电压耐受能力1.3 p.u.（基波正序电压），暂态过电压问题成为威胁新能源汇集地区送电安全的决定性因素，这使得电网调度部门以“不发生暂态过电压”为原则制定新能源送出通道的送电极限［7］。因此，有必要深入分析暂态过电压问题的形成原因，从而制定更为科学的送电极限校核方案，在保证系统稳定的前提下尽可能增加新能源的送出。针对该问题的研究主要有如下2类。

第1 类是针对新能源发电经特高压直流送出系统这一特殊场景的研究。文献［8］从系统仿真建模、暂态过电压根源解析、抑制策略设计3 个方面进行总结，指出直流线路闭锁和受端换相失败均可导致暂态过电压。文献［9-11］对换相失败产生的暂态过电压问题进行全面分析，其中：文献［9］根据基于线性整流换流器的高压直流输电（line-commutated converter HVDC，LCC-HVDC）受端换相失败引发送端暂态电压的动态过程建立暂态过电压峰值解析模型；文献［10］根据上述模型揭示不同类型机组与LCC-HVDC 暂态无功电压的作用机理；文献［11］提出计及虚拟磁链的永磁同步发电机控制策略，对机组在LCC-HVDC换相失败故障下的暂态过电压进行抑制。文献［12］推导交直流故障后换流站和风机侧暂态电压幅值的理论计算公式，分析交直流故障引发暂态过电压的机理，指出风机低电压穿越期间的无功、有功出力对暂态过电压的影响。

第2 类是针对风机自身控制和临近无功补偿设备动作导致的暂态过电压研究。文献［13］针对线路单相接地保护动作后风电场联络线非全相运行的情况，分析故障相恢复电压特性及其影响因素。文献［14］基于典型电压穿越策略建立永磁直驱风机并网模型，研究永磁直驱风机在弱电网中送出线路远端短路故障时的功率特性，指出远端短路故障清除时的锁相环误差是暂态过电压的重要影响因素。文献［15］指出动态无功补偿设备无法正常投运感性支路是造成暂态过电压的重要原因。文献［16］认为短路故障清除后电压骤升导致风机脱网的原因应包括风机自身的动态无功控制响应滞后或控制超调。

上述研究存在以下特点：使用有效值而非瞬时值衡量过电压峰值；重点分析传统直流输电送端场景；认为无功盈余是产生过电压的原因。文献［17］基于华北地区新能源送出系统的仿真与实际运行经验指出，新能源汇集经交流线路送出存在故障后的过电压问题，且过电压应划分为3 个阶段，分别是操作过电压阶段、LC 谐振阶段和无功盈余工频过电压阶段。大多研究分析操作过电压和无功盈余工频过电压的产生机理与应对措施，而未考虑LC谐振阶段的暂态过电压，但实际制约新能源送出系统输电极限的过电压时间尺度正好对应LC谐振阶段。

综上，本文研究由LC 谐振引起的暂态过电压问题。通过电磁暂态仿真分析新能源送出系统交流短路故障下暂态过电压的形态特征，分析不同系统参数对暂态过电压特征的影响，利用RLC 电路的全响应理论阐述暂态过电压的产生机理，并对各类现象进行解释。

1 暂态过电压的形态特征

1.1 新能源汇集系统模型的建立

为分析新能源汇集系统短路故障过程的暂态过电压问题，基于华北电网典型风电汇集系统的具体参数（如附录A 表A1 所示）建立如图1 所示的仿真模型，图中N为新能源机组数量。

在图1 中：对500 kV 及以上电压等级的系统进行戴维南等效处理；对系统中各电压等级的传输线路和汇集线路均采用π 型等值电路进行建模，线路与变压器的参数均为实测参数；采用某新能源设备厂商提供的2 MW 双馈风机黑箱Simulink 模型作为新能源机组模型。为验证风机黑箱Simulink 模型的有效性，仿照型式试验工况，基于文献［18］的对比方法，对比三相电压深度跌落持续625 ms 的过程中Simulink 模型与型式试验结果，如图2 所示（图中机端电压、机端有功功率、机端无功功率均为标幺值）。由图可知，Simulink 模型与型式试验的功率动态特性基本一致，这说明Simulink 模型可以用于模拟该型号风机的真实故障响应特性。

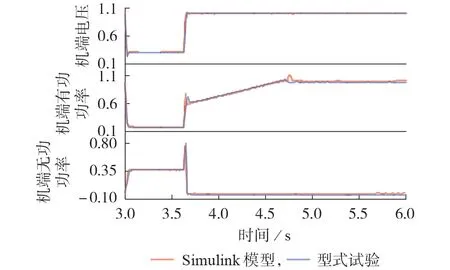
图2 Simulink模型与型式试验结果对比Fig.2 Results comparison between Simulink model and type test

1.2 典型故障下的暂态过电压仿真

基于图1 系统开展仿真研究，设定风机开机数量为50台，风机单机出力为100 % 的额定有功功率，故障位置为500 kV 传输线路靠近500 kV/220 kV 变压器的一侧。

对以下2 种典型故障进行电磁暂态仿真：单回线A 相发生单相瞬时性故障（简称单瞬故障）；双回线一回发生三相永久性故障（简称三永故障）。风电场主变（即220 kV/35 kV 变压器）高压侧的三相电压瞬时值如图3 所示（图中电压为以220 kV 为基准值的标幺值，后同），其中图3（b）为图3（a）故障清除时刻附近的放大图。

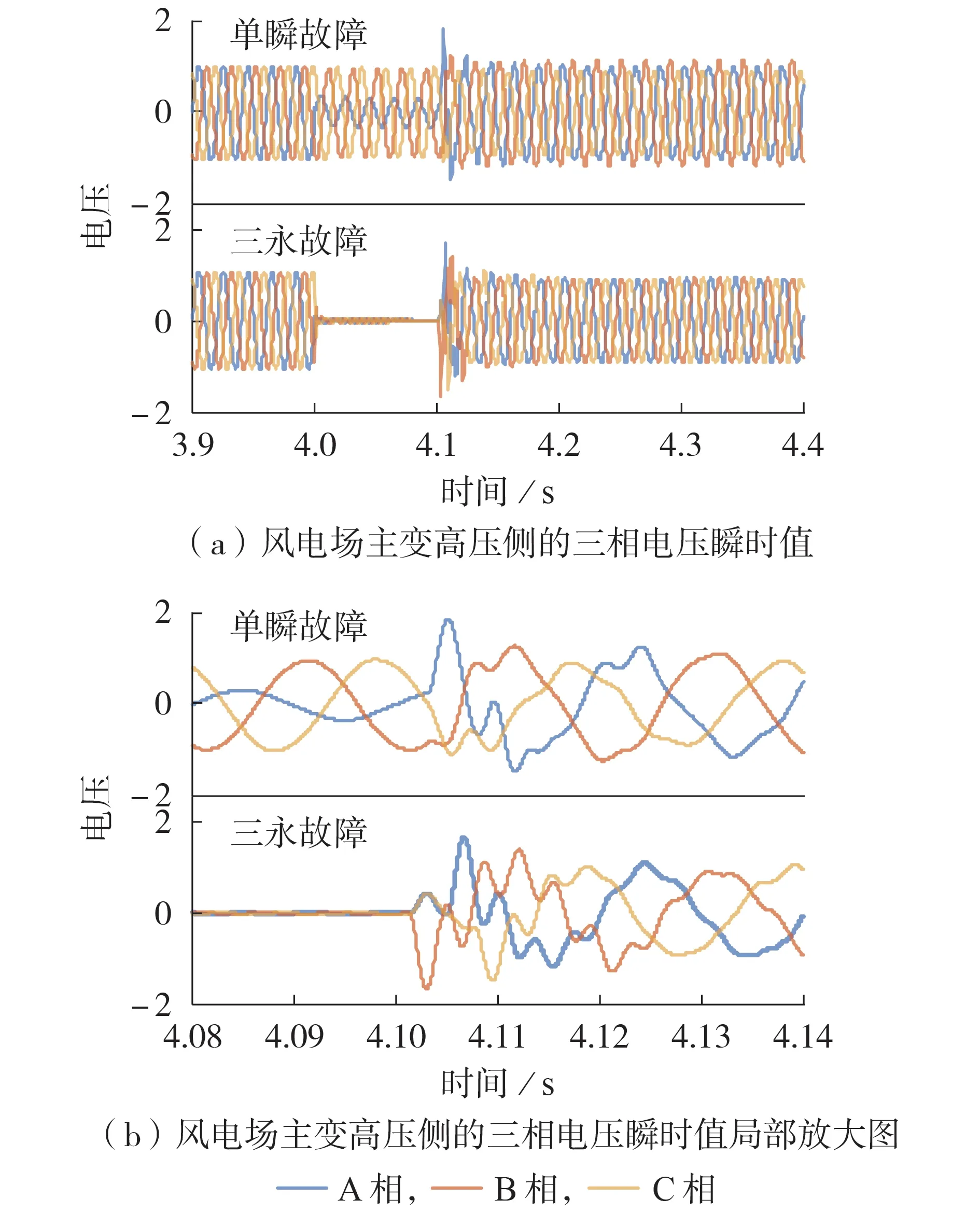
图3 典型故障下风电场主变高压侧的三相电压瞬时值Fig.3 Three-phase voltage instant values on high-voltage side of main transformer of wind farm under typical faults

由图3 可知，单瞬故障和三永故障下过电压均出现在断路器跳开后，电压瞬时值峰值分别达到1.88、1.68 p.u.，超过我国国家标准中要求的新能源高电压耐受能力1.3 p.u.。

图3（b）中断路器跳开后的故障相电压除了基频分量外，还存在百赫兹级的高频分量。采用Prony方法对各工况中断路器跳开前后时刻的A 相瞬时电压进行小波分析，分离出基频与高频分量，如图4所示。

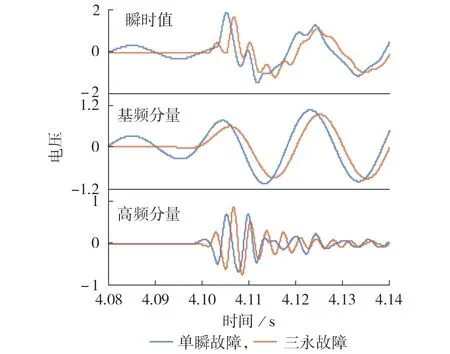
图4 典型故障下A相电压瞬时值的基频与高频分量Fig.4 Fundamental frequency and high frequency components of phase A voltage instant values under typical faults

由图4 可知，在单瞬故障和三永故障下，断路器跳开后产生的暂态过电压具有相似的形态，其主要组成部分为基频分量和高频分量。

为验证图1 所示系统仿真所得过电压特征的真实性，在图1 对应的实际新能源汇集系统进行短路试验，设置500 kV 线路A 相发生单瞬故障，并对故障清除且未重合闸的过程进行录波，得到风电场主变高压侧三相电压的故障波形，如附录A 图A1所示。可见，实际系统存在与图1 所示系统仿真结果类似的暂态过电压特征，即存在由高频分量导致的暂态过电压问题。需说明的是，GB／T 19963.1—2021《风电场接入电力系统技术规定 第1 部分：陆上风电》与GB／T 19964—2012《光伏发电站接入电力系统技术规定》中新能源应具备的高电压穿越能力要求所针对的过电压均非瞬时值，即现行标准未给出新能源机组应具备何种应对高频分量过电压的能力，这是困扰新能源汇集系统运行的实际问题。

2 暂态过电压瞬时值的影响因素

下面基于华北地区典型新能源汇集系统参数，分析风机单机出力、风机开机数量、送出线路长度对暂态过电压的影响规律。

1）风机单机出力的影响。

将风机开机数量固定为50 台，设置风机单机出力分别为20 %、40 %、60 %、80 %、100 % 的额定有功功率。单瞬故障与三永故障下断路器跳开后风电场主变高压侧的暂态过电压最高相情况如附录A 图A2 所示。随着风机单机出力水平的提升，单瞬故障下断路器跳开后的暂态过电压峰值逐渐增加：风机单机出力为20 % 的额定有功功率时，暂态过电压峰值为1.71 p.u.；风机单机出力增加到100 % 的额定有功功率时，暂态过电压峰值达到1.88 p.u.。对于单瞬故障下高频分量的频率：风机单机出力为20 % 的额定有功功率时，频率约为261 Hz；风机单机出力增加到100 % 的额定有功功率时，频率下降到210 Hz左右。三永故障下断路器跳开后A 相暂态过电压形态受新能源单机出力水平的影响较小：风机单机出力为20 % 的额定有功功率时，暂态过电压峰值为1.65 p.u.；风机单机出力增加到100 % 的额定有功功率时，暂态过电压峰值为1.69 p.u.。三永故障下高频分量的频率始终保持在270 Hz左右。

2）风机开机数量的影响。

将风机单机出力固定为100 % 的额定有功功率。设置风机开机数量分别为10、30、50、70 台。单瞬故障和三永故障下断路器跳开后风电场主变高压侧的暂态过电压最高相情况如附录A 图A3 所示。随着风机开机数量的增加，单瞬故障下暂态过电压峰值逐渐降低：风机开机数量为10 台时，暂态过电压峰值为2.15 p.u.；风机开机数量增加到70台时，暂态过电压峰值降低到1.73 p.u.。对于单瞬故障下高频分量的频率：风机开机数量为10 台时，频率约为271 Hz；风机开机数量增加到70 台时，频率下降到190 Hz左右。三永故障下断路器跳开后的暂态过电压形态受风机开机数量的影响较小：风机开机数量为10台时，暂态过电压峰值为1.73 p.u.，风机开机数量增加到70台时，暂态过电压峰值下降到1.67 p.u.。三永故障下高频分量的频率基本保持在270 Hz左右。

3）220 kV送出线路长度的影响。

将风机开机数量固定为50 台，风机单机出力固定为100 %的额定有功功率，设置220 kV 送出线路长度分别为20、30、60、90、120 km。单瞬故障和三永故障下断路器跳开后风电场主变高压侧的暂态过电压情况如附录A 图A4 所示。随着220 kV 送出线路长度的增加，单瞬故障下断路器跳开后的暂态过电压峰值先上升后下降，220 kV 送出线路长度为20、60、120 km 时的暂态过电压峰值分别为1.68、1.88、1.84 p.u.。单瞬故障下高频分量的频率基本保持在200 Hz 左右。三永故障下断路器跳开后的暂态过电压峰值受220 kV 送出线路长度的影响不大，但呈现出先下降后上升的趋势，送出线路长度为20、60、120 km 时的暂态过电压峰值分别为1.72、1.68、1.79 p.u.。三永故障下高频分量的频率基本保持在270 Hz左右。

4）500 kV送出线路长度的影响。

将风机开机数量固定为50 台，风机单机出力固定为100 % 的额定有功功率。设置500 kV 送出线路长度分别为60、100、200、300、400 km。单瞬故障和三永故障下断路器跳开后风电场主变高压侧的暂态过电压情况如附录A图A5所示。单瞬故障和三永故障下500 kV送出线路长度对暂态过电压形态的影响均很明显，该影响来自高频分量。采用Prony方法对断路器跳开时的瞬时电压进行小波分析，提取高频分量，如图5所示（图中电压高频分量为标幺值）。

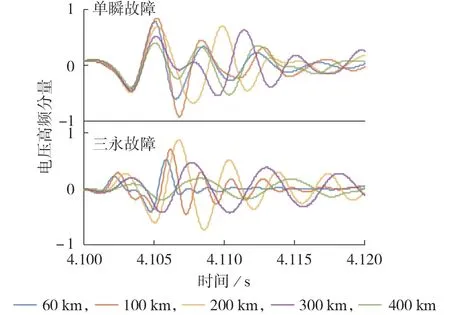
图5 不同500 kV送出线路长度下的暂态过电压高频分量Fig.5 High-frequency components of transient overvoltage under different lengths of 500 kV sending lines

随着500 kV 送出线路长度的增加，单瞬故障下断路器跳开后的暂态过电压峰值变化较小：500 kV送出线路长度为60～300 km 时，暂态过电压峰值保持在1.88 p.u.左右；500 kV 送出线路长度为400 km时，暂态过电压峰值下降至1.78 p.u.。单瞬故障下高频分量的频率与500 kV送出线路长度没有明显的单调关系，在200～300 Hz 变化。随着500 kV 送出线路长度的增加，三永故障下断路器跳开后的暂态过电压峰值呈现先上升后下降的趋势。三永故障下高频分量的频率随着500 kV 送出线路长度的增加而显著下降，500 kV 送出线路长度为60、200、400 km时的高频分量频率分别约为678、270、154 Hz。

各因素对暂态过电压的影响如附录A 表A2 所示。结合表A2以及图A1 —A4和图5的仿真结果可得如下结论：

1）风机单机出力水平的增加会导致暂态过电压峰值的上升，而风机开机数量的增加反而会使暂态过电压峰值降低；

2）三永故障下暂态过电压的高频振荡模态主要由500 kV送出线路长度决定。

3 暂态过电压的成因分析

下面以三永故障为例分析断路器跳开后出现暂态过电压的成因。由第2 章可知，三永故障下暂态过电压的频率、幅值等模态主要受500 kV 送出线路长度影响，受500 kV 电压等级以下的设备影响较小。因此，假设系统在500 kV/220 kV 变压器低压侧断开，将图1 所示的仿真系统进行简化，如附录A 图A6所示。图A6中，2条500 kV 线路均是π 型等值线路，且存在不可忽视的相间电容和相间互感，难以直观地用于分析故障后断路器跳开导致的暂态过电压，需要对模型进行进一步简化。为此，需分析故障清除后的电路动态。设置发生双回线三永故障，在清除一回线后，故障点断路器外侧的三相电压（即Va、Vb、Vc）和该处送往故障点的电流如图6 所示（图中t1、t2、t3分别为B、A、C相断路器跳开时刻）。

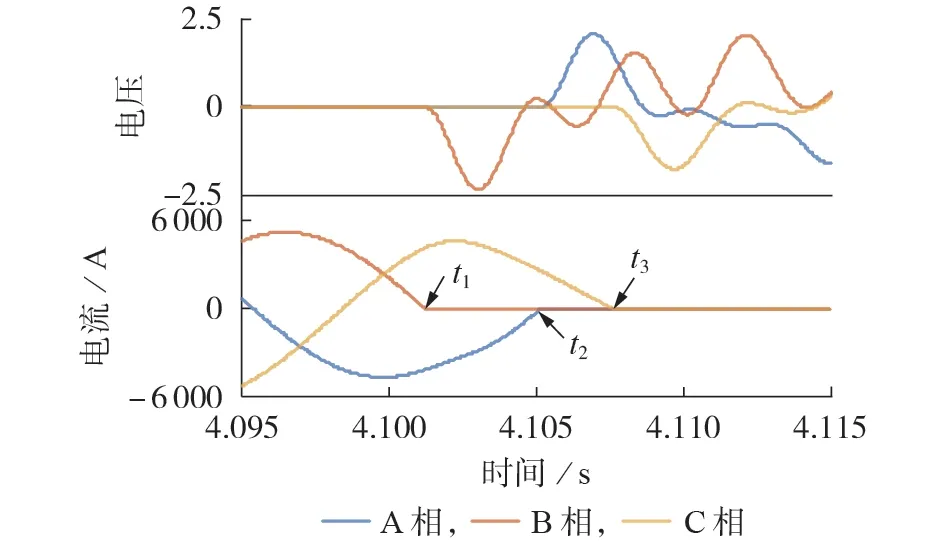
图6 故障清除后的电路动态Fig.6 Circuit dynamics after fault removal

由图6 可知，交流断路器必须在电流过零时才能跳开，三相断路器实际上是依次关断的，具体如下。

1）在t1时刻，B 相电流过零，B 相断路器最先跳开，与故障点断开联系，图A6 中Vb处的B 相电容Cg开始充电。在A 相电流过零，断路器跳开前，只有B相存在电压，其他两相均保持接地。

2）在t2时刻，A 相电流过零，A 相断路器跳开，之后A 相电容开始充电。同理，在t3时刻，C 相电流过零，C相断路器跳开，之后C相电容开始充电。

鉴于图6 中B 相电压最高，由于三相对称，不失一般性，分析从B 相断路器跳开后至A 相断路器跳开前时段内B 相电压的变化过程。由于该时段内的电路结构不变，可将系统进行进一步简化，如图7（a）所示。图7 中：usa、usb、usc为系统三相电压；Rs、Ls分别为系统电阻、电感；Rz、Lz分别为线路的自电阻和自电感；Rm、Lm分别为线路的互电阻和互电感；Cg、Cp分别为线路靠近变压器一侧的π 线对地电容和相间电容；i1、i2、i3分别为注入故障点的B、C、A 相电流。根据图7分析该时段内的B相电压、电流，可知：

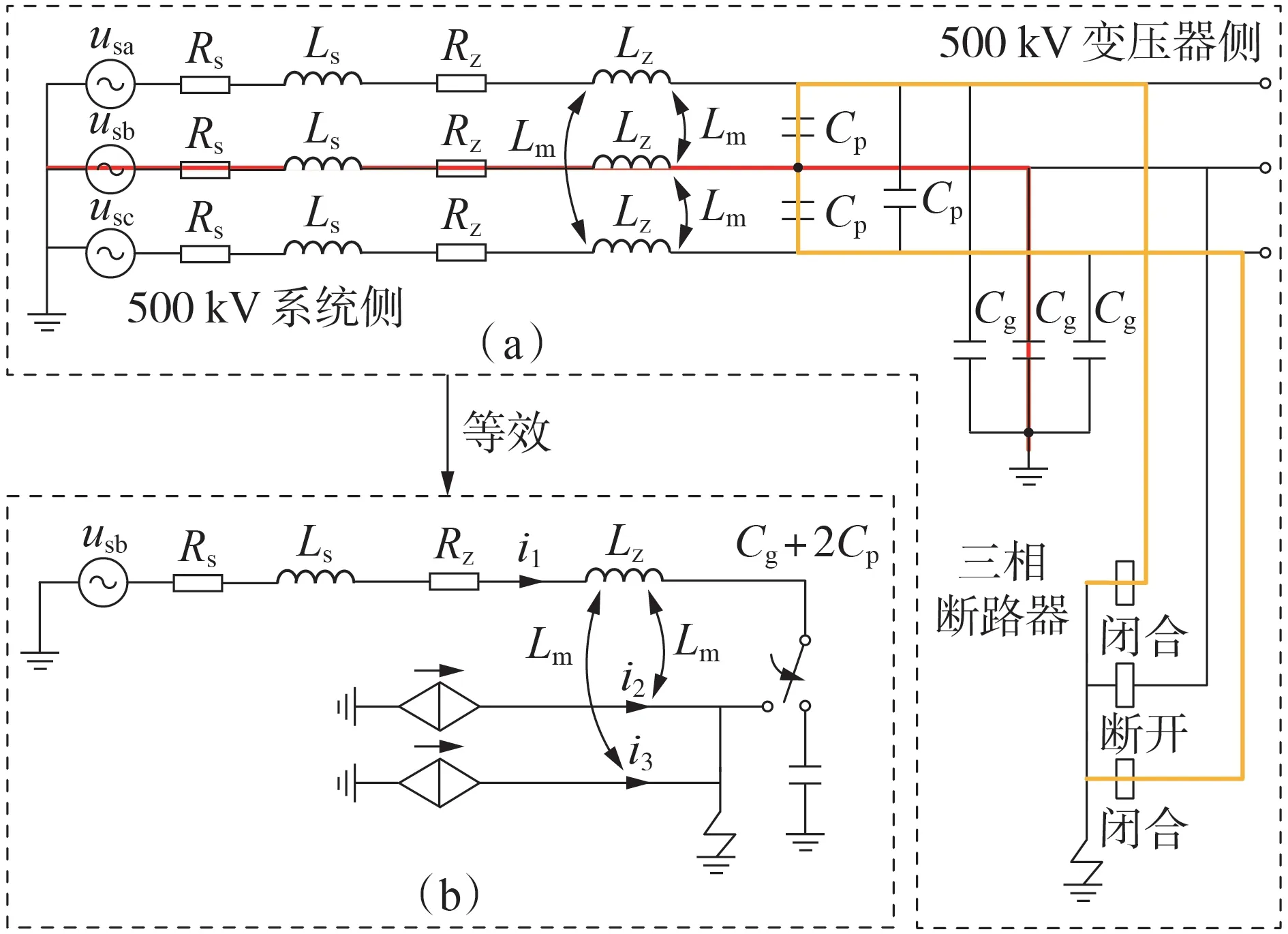
图7 三相故障后三相系统的单相等效系统Fig.7 Single-phase equivalent system of three-phase system after three-phase fault

1）B 相系统侧电压源通过系统电阻Rs、系统电感Ls和B 相线路靠近变压器一侧的π 线对地电容Cg充电，回路如图7（a）中红色实线所示；

2）由于A相和C相处于接地状态，B相系统侧电压源同时对B 相与A、C 相间的相间电容Cp充电，回路如图7（a）中橙色实线所示；

3）A 相和C 相的故障电流通过线路互感Lm作用于B相，在B相上产生附加的感应电压。

由此，可以绘制出该时段内B 相的等效电路，如图7（b）所示。根据等效电路可列出电路方程：

同样地，线路的自电感Lz、自电阻Rz和互电感、Lm、互电阻Rm根据线路的正序电感L1、正序电阻R1和零序电感L0、零序电阻R0计算得到，即：

由式（2）可知：等号左侧为RLC 串联电路二阶微分方程的典型形式；等号右侧包含B 相电压usb以及C、A 相电流i2、i3，考虑到此时C、A 相处于故障未清除状态，其故障电流很大，可忽略B 相通过互感对C、A相故障电流造成的影响，因此，认为C、A相的故障电流仅与其自身对地回路的阻抗有关，利用短路电流的计算方法很容易计算电流i2、i3，并将其作为激励通过互感作用于B 相，至此，等号右侧均为已知量，根据三角函数的特性，等号右侧可以看作是一个工频的正弦电压激励。由此可见，在从B 相断路器跳开后至A 相断路器跳开前，B 相电压、电流的模型为典型RLC串联二阶电路的全响应模型。

图8 展示了式（2）所示B 相等效电路与图A6 所示完整三相电路的电压波形对比。由图可知，两电路的结果十分接近，采用等效电路仿真得到的暂态过电压峰值误差在5 % 以内。

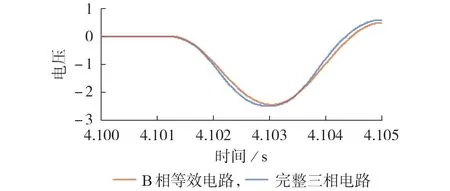
图8 B相等效电路与完整三相电路的电压波形对比Fig.8 Comparison of voltage waveforms between phase B equivalent circuit and complete three-phase circuit

根据上述分析，可以对暂态过电压的成因以及部分仿真结果进行如下机理解释。

1）故障后断路器跳开导致的暂态过电压的成因为：断路器跳开后，系统中电源通过线路为故障点的线路电容充电。

2）暂态过电压的高频分量为二阶系统RLC 参数决定的谐振分量。

3）三永故障下高频分量的频率随着送出线路长度的增加而下降的原因为：高频分量由RLC 串联谐振产生，其模态由500 kV 线路主导。二阶电路的谐振频率F=1/［2π（LC）0.5］，显然F与送出线路长度成反比关系，与图5中的情况基本吻合。

由于单瞬故障属于不对称故障，涉及变压器接线方式、对地阻抗等问题，最小等效电路需进一步向低压侧延伸，包含220 kV 传输线和220 kV/35 kV 变压器，这使得系统结构不易简化，难以抽象出低阶的等效电路模型，因此，本文暂不讨论单瞬故障的暂态过电压数学模型。单瞬故障下高频分量的本质与三永故障相同，均为系统RLC参数决定的谐振分量。

4 结论

本文基于华北地区典型新能源汇集系统参数，建立适用于暂态过电压仿真的电磁暂态模型，对短路故障下断路器跳开导致的暂态过电压问题进行机理分析。分析结果表明，暂态过电压的波形主要为工频分量和高频分量的叠加，其峰值与风机单机出力呈正相关，而与风机开机数量呈负相关，且当故障发生在500 kV 线路末端的情况下，暂态过电压模态受500 kV 送出线路长度影响很大。本文对双回传输线三永故障建立的简化等效数学模型进一步说明了暂态过电压的本质来源是RLC 电路的全响应，暂态过电压的高频分量来自电路的固有谐振。

笔者后续将研究单瞬故障的等效电路建模和单瞬故障的暂态过电压机理，并定量分析新能源机组对该暂态过电压的影响。

附录见本刊网络版（http：//www.epae.cn）。