基于事件优化理论的“风-储-荷”联合单元最优平抑控制策略

孙 乾，李翠萍，李 江，李军徽

（1.东北电力大学 电气工程学院，吉林 吉林 132012；2.上海电力大学 电气工程学院，上海 200090）

0 引言

风能具有随机性和间歇性的固有缺陷，现有风电出力预测精度不足，即使是最好的预测系统也无法消除与特定预测相关的不确定性［1］。发电量和耗电量的变化与预测的高度不确定性相组合，使得风力发电更难适应电力系统的常规运行［2］。大规模风电接入电网，会给系统的安全稳定运行［3］、高风险爬坡事件平抑带来巨大的挑战［4］。

在储能备用深调空间逐步用尽的背景下，风电正步入“后补贴”甚至“无补贴”时代［5］，风力发电平价、竞价上网，项目竞标并网，促使风电回归真实价值［6］。然而，风能的固有缺陷削弱了风电在电力市场中的竞争力，使得“风-储-荷”联合单元的平抑效益大幅降低［7］。因此，亟需引入高效的辅助服务市场机制，利用市场制度提高备用资源平抑灵活性，充分挖掘储能备用平抑空间［8］。

近年来，事件优化（event-based optimization，EBO）理论已被应用在诸多领域，尤其是在解决离散动态系统的问题规模及复杂性方面得到了进一步的发展。文献［9］采用基于事件的控制方法，使控制器仅在客户到达事件发生时做出决策，证明了最优控制策略具有阈值形式。文献［10］通过EBO 理论对策略空间进行参数化，设计了基于扰动梯度算法找出局部最优的策略。文献［11］在拉格朗日松弛框架内，开发了基于EBO 理论的暖通空调系统节能最优控制策略求取算法，将不确定性汇总为几个关键因素，并在事件的定义中包含这些关键因素和其他随时间变化的变量，然后采用Q 学习替代拉格朗日方法和样本平均逼近来解决维数灾问题。目前，关于风电平抑控制策略的研究大多以“点功率”作为分析对象，无法实现EBO 运行；EBO 理论在电气领域的应用大多局限于选择一个动作，使得系统达到当前最大的期望“潜在”平均收益，并未考虑当前动作对系统长期运行的影响，因此也被称为贪婪EBO理论。

本文引入辅助服务市场机制，以市场出清电价激励储能系统积极参与平抑，提高“风-储-荷”联合单元的效益以及电网的运行可靠性。定义了以能量为依据的风电不确定事件，以事件为研究主体，相较于以状态为研究主体，减少了策略空间，加快了决策速度。提出了一种策略梯度迭代在线算法，可以同时考虑系统当前平抑收益及长期平均收益，得到平抑效果与平抑效益最优的“风-储-荷”联合单元最优平抑控制策略。

1 EBO理论中事件的基本概念

1.1 风电不确定事件能量化

1.1.1 离散风电功率能量化

为了准确计算风电爬坡成本，本文根据风电机组的运行点确定风电机组的爬坡率。假设风电爬坡事件特征为一个线性分段函数［12］，如式（1）所示。

根据风电机组的爬坡率可得到爬坡持续时间及能量，分别如式（2）和式（3）所示。

1.2 “风-储-荷”联合单元状态

式中：T为时段总数，考虑到本文针对日前平抑控制策略并以15 min为时段间隔，则T=96。

1.3 EBO理论中事件的定义

在EBO 理论的离散事件系统模型内部，事件被定义为具有某些共同特性的状态转移集合，而动作的选择取决于事件的相关信息。系统结构特性和系统动作之间的逻辑关系能够由事件描述，其中包含了3 类“同时”发生的事件，共同决定1 个转移，并且具有时间上的逻辑顺序［13］。

1）可观事件。

2）可控事件。

基于刚发生的可观事件所得到的信息，可以控制其发生概率的事件被称为可控事件。一般地，当风电功率在4 h 内的能量波动至少达到装机容量的50 % 时，才认定发生爬坡事件［14］。为了进一步减小策略优化的计算量，本文设置风电能量波动的允许

3）自然转移事件。

自然转移事件对应的转移由系统的属性决定，因此自然转移事件发生的概率不可控。

对比式（6）所示系统状态空间S可知，可观事件空间小于系统状态空间，且通过设定风电能量波动允许区间得到可控事件空间，使得事件空间大小进一步减小，大幅减少了计算空间。这是EBO 理论的重要优势［15］。

1.4 EBO理论中的状态转移概率

在电力系统中，多个部件同时发生故障几乎是不可能的，故一般以系统中某个关键部件的历史故障状态转移概率作为系统的故障状态转移概率。根据系统故障状态转移概率，本文以满足特定期望和标准差的正态分布表示系统正常运行条件下的状态转移概率［16］。

1.5 风电不确定事件的初始平抑控制策略

1.5.1 EBO理论的2个基本量

基于EBO 理论的策略优化方法可以自然地处理风电不确定事件触发联合单元备用容量进行策略的性能优化，使得联合单元在平抑效益最大化的同时，平抑效果最优。该优化方法基于2 个基本量，即性能、事件Q 因子［17］。可以从系统样本路径中估算这2 个基本量，且可以通过策略梯度迭代地改进平抑控制策略，量化（事件-动作）对性能的长期影响。

在EBO 理论中，系统性能评价指标可以是任何

Q因子作为性能势的一个变形，即状态st的平均性能势，其含义为：当系统处于状态st下，观测到某事件e发生，采取决策d且执行某动作a时，该动作为联合单元所产生的效益。EBO 理论中的事件Q因子与马尔可夫决策过程（Markov decision process，MDP）中的事件Q因子类似，可表示为：

1.5.2 基于贪婪EBO理论求解初始平抑控制策略式中：ati(t=1，2，…，T；i=1，2，…，N) 为t时段第i条样本路径的动作，若ati=ERup/Rdnt，则表示当风电不确定事件引发联合单元能量失衡后，向电力辅助服务市场进行招标上调备用／投标下调备用；若ati=0，则表示联合单元不动作。若投标下调备用，则联合单元获得收益；若招标上调备用，则联合单元产生平抑成本。

根据贪婪EBO 理论，取Q 因子最大的动作作为该时段的初始决策，即：

式中：dt(ec)为t时段的最优决策动作。

贪婪EBO 理论算法简单易行，但只保证了当前时段的平抑效果，未考虑对后续时段性能的影响。本文提出了一种策略梯度迭代在线算法，以策略梯度确定迭代方向，得到同时考虑平抑效果与性能的最优平抑控制策略。为了方便求解策略梯度，与基于MDP 的策略梯度优化算法类似，策略用归一化指数函数Softmax函数表示［19］，如式（14）所示。

式中：μθ(a|ec)为控制策略；b为动作空间A中的样本动作；θ(ec，a)=ec-d(ec)为采取动作a时的策略参数。一般而言，μθ(a|ec)相对于θ是连续可微的，则策略μθ是策略参数θ和可控事件ec在动作空间A中的概率分布。

2 基于EBO 理论的风电不确定事件平抑控制策略优化

2.1 风电不确定事件的平抑模型

为了有效应对源-荷侧双向不确定性、波动性引起的功率失衡，需要综合利用包括储能系统、辅助服务市场在内的多种灵活性备用资源。引入辅助服务市场机制，可提高联合单元的运行稳定性；鼓励储能系统投入辅助服务市场，可利用市场制度提高备用容量平抑灵活性，充分挖掘源-荷-储侧多元资源的调节能力，提高风电并网消纳率与风电场的效益。

2.1.1 联合单元的平抑成本

1）辅助服务市场备用成本。

辅助服务市场备用成本CREt包含招标上调备用容量成本和投标下调备用容量成本，可表示为：

2）储能系统平抑成本。

考虑到储能充放电电量、充放电循环次数对寿命的影响，建立储能损耗成本模型［20］，将联合单元的电能供需差储能系统的剩余备用容量二者间的最小量作为储能系统的动作量，以保证储能系统不会超出自身调节能力，则储能系统平抑成本CESt可表示为：

2.1.2 联合单元的平抑目标函数

综合考虑储能备用容量匹配度及平抑效益构建目标函数［21］，用以估计策略性能，如式（19）所示。

2.2 求解最优平抑控制策略

2.2.1 确定策略梯度

利用不同策略下系统结构的一些“知识”（性能），通过研究1 个策略下的系统行为（动作），可以确定该策略小邻域内的性能，即确定策略梯度。假设对于任何策略参数θ′和θ而言，条件概率πθ′s(i|e)具有以下性质：

2.2.2 策略梯度迭代在线算法

为了解决风电不确定事件的平抑问题，本文基于EBO 理论制定事件决策过程，利用基于敏感度分析的方法，结合事件的性能梯度估计算法和事件在线策略迭代算法，提出了一种基于策略梯度公式的策略迭代在线算法，用于求解基于事件的最优平抑控制策略［22］，具体步骤如下。

1）能量化样本功率数据，生成风电可控事件。

2）判断储能系统自身是否能够完成平抑，若自身能够完成平抑，则以动作a=0 作为初始决策；否则，构建事件Q因子，根据贪婪EBO理论算法生成初始决策（动作）。

3）生成动作空间A，形成初始平抑控制策略。

2.3 算法评价指标

本文以长期平均收益作为平抑效益评价指标，为了进一步体现策略梯度迭代在线算法平抑效果的优势，提出了基于功率的平抑效果评价指标，并通过功率还原算法还原不同策略下联合单元的输出能量。

1）平抑偏差平均值Δδ。

3 算例分析

以冀北某风电场2020 年3 月和10 月某天的风电功率数据、负荷功率数据作为日前预测样本数据，并以15 min 为采样分辨率，共采集96 个离散功率点。风电场的装机容量为20 MW，储能系统以抽水蓄能电站为例，最大储存能量为20 MW·h，当天00:00 时刻的初始储存能量为10 MW·h。15 min 内的能量波动允许值为0.8 MW·h。辅助服务市场的阶梯出清电价见附录A 表A1。储能系统单位充放电电量惩罚系数为200 元／（MW·h）［20］。考虑到电力系统持续稳定运行的要求，设储能备用容量匹配度的加权参数λ1=0.7，平抑效益的加权参数λ2=0.3。

3.1 系统初始能量状态及能量型事件

首先分别根据式（4）和式（5）将3 月、10 月的预测离散风电功率、负荷功率数据能量化，分别如附录A 图A2—A5所示。根据风电离散能量值、负荷离散能量值得到3月、10月的能量型风电可控事件，分别见附录A 图A6 和图A7。由图A6 可知：3 月的风电可控事件中，20 —35 时段的风电功率陡增，而负荷需求并不高，此时为风电爬坡事件；60 —80 时段的风电功率陡降，而负荷需求较大，此时为风电下坡事件。由图A7 可知，10 月的风电可控事件中，20 —55时段为风电下坡事件，65 —90 时段为风电下坡事件。上述结果反映了风电应用的复杂性，即大规模风电并网后，传统的单侧波动将转变为电源侧和负荷侧的双侧波动。

3.2 平抑效果比较

初始平抑控制策略下3 月、10 月的储能剩余容量分别见附录A 图A8 和图A9。由图可知：贪婪EBO理论算法下的初始平抑控制策略仅考虑了平抑动作对当前时段平抑效益的影响，没有考虑当前动作对系统长期平均收益的影响，导致3 月储能系统在27 —34 时段的剩余容量达到最大值，10 月储能系统在85 —90 时段的剩余容量降低为0，短时间内抽水蓄能电站失去了调节能力，这会给系统之后的稳定运行带来风险。且储能剩余容量长时间处于极限状态，会降低抽水蓄能电站的使用寿命。

不同样本路径下的动作空间如附录A 图A10 所示，通过策略梯度迭代在线算法以性能梯度更新策略参数，基于Softmax 函数得到3月和10月动作空间的概率分布，即最优平抑控制策略下各时段的最优决策（动作），分别如图1和图2所示。

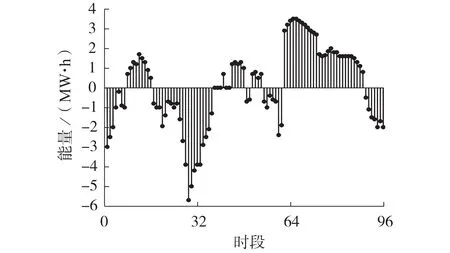
图1 最优平抑控制策略下3月的最优动作Fig.1 Optimal action in March under optimal smoothing control strategy

图2 最优平抑控制策略下10月的最优动作Fig.2 Optimal action in October under optimal smoothing control strategy

在3 月风电事件中：20 —35 时段发生风电爬坡事件，此时市场出清价格为谷时电价，且抽水蓄能电站的容量已接近峰值，联合单元主要采取向辅助服务市场投标下调备用的动作来平抑，以减少电站的充电量，为之后消纳风电做准备；60 —80 时段发生风电下坡事件，其中60 —71时段市场出清价格为平时电价，但在72 —80时段市场出清价格达到峰时电价，因此联合单元在前期主要采取向辅助服务市场招标上调备用的动作来平抑以减少电站的放电量，为之后出清价格峰时减少招标上调备用做准备。在10 月风电事件中，20 —55 时段发生风电下坡事件，40 —69时段的市场出清价格为峰时电价。因此，联合单元尽可能地减少辅助服务市场招标上调备用的动作来平抑，而是利用抽水蓄能电站放电来降低平抑成本。初始平抑控制策略下3 月、10 月的长期平均收益分别为1 178.48、1 247.50 元／时段。最优平抑控制策略下3月、10月的储能剩余容量分别如图3和图4 所示。由图可知：最优平抑控制策略基于辅助服务市场机制灵活地调用抽水蓄能电站，充分挖掘了储能备用的平抑空间，同时能够在全时段时间尺度下考虑当前及长期平均收益，3 月、10 月的长期平均收益分别达到1 378.5、1 394.0元／时段。

图3 最优平抑控制策略下3月的储能剩余容量Fig.3 Residual capacity of energy storage in March under optimal smoothing control strategy

图4 最优平抑控制策略下10月的储能剩余容量Fig.4 Residual capacity of energy storage in October under optimal smoothing control strategy

3.3 不同算法的平抑效果比较

考虑到EBO 理论脱胎于传统的MDP，基于3 月的风电功率、负荷功率数据，采用式（30）和式（31）对比分析基于策略梯度迭代在线算法的最优平抑控制策略与文献［23］中基于马尔可夫预测模型的粒子群优化算法的控制策略的平抑效果，结果如表1 所示。由表可知：相较于平抑前，基于策略梯度迭代在线算法和粒子群优化算法所得的平抑偏差平均值、平抑偏差最大值均减小，表明2 种算法均可有效平抑；且相较于粒子群优化算法，策略梯度在线迭代算法的平抑效果更优。不同算法下联合单元的输出功率如图5 所示。由图可知，相较于平抑前，基于2 种算法均能取得较好的平抑效果，但策略梯度迭代在线算法下输出功率的波动幅值大小与频率均比粒子群优化算法小，整体输出功率更趋于稳定。

表1 不同算法下的平抑效果Table 1 Smoothing effect under different algorithms

图5 不同算法下联合单元的输出功率Fig.5 Output power of joint unit under different algorithms

不同算法下的平抑效益如图6 所示。由图可知，虽然在某些时段，策略梯度迭代在线算法的平抑效益低于粒子群优化算法，但从全时段整体上而言，策略梯度迭代在线算法的长期平均收益高于粒子群优化算法。不同算法所得长期平均收益比较如图7所示。由图可知，策略梯度迭代在线算法所得长期平均收益随着迭代次数的增大而快速增大，在经过600次迭代后趋于恒定，经过800次迭代后已能满足风电能量波动的允许区间，并在1 000次迭代结束时性能达到最优。

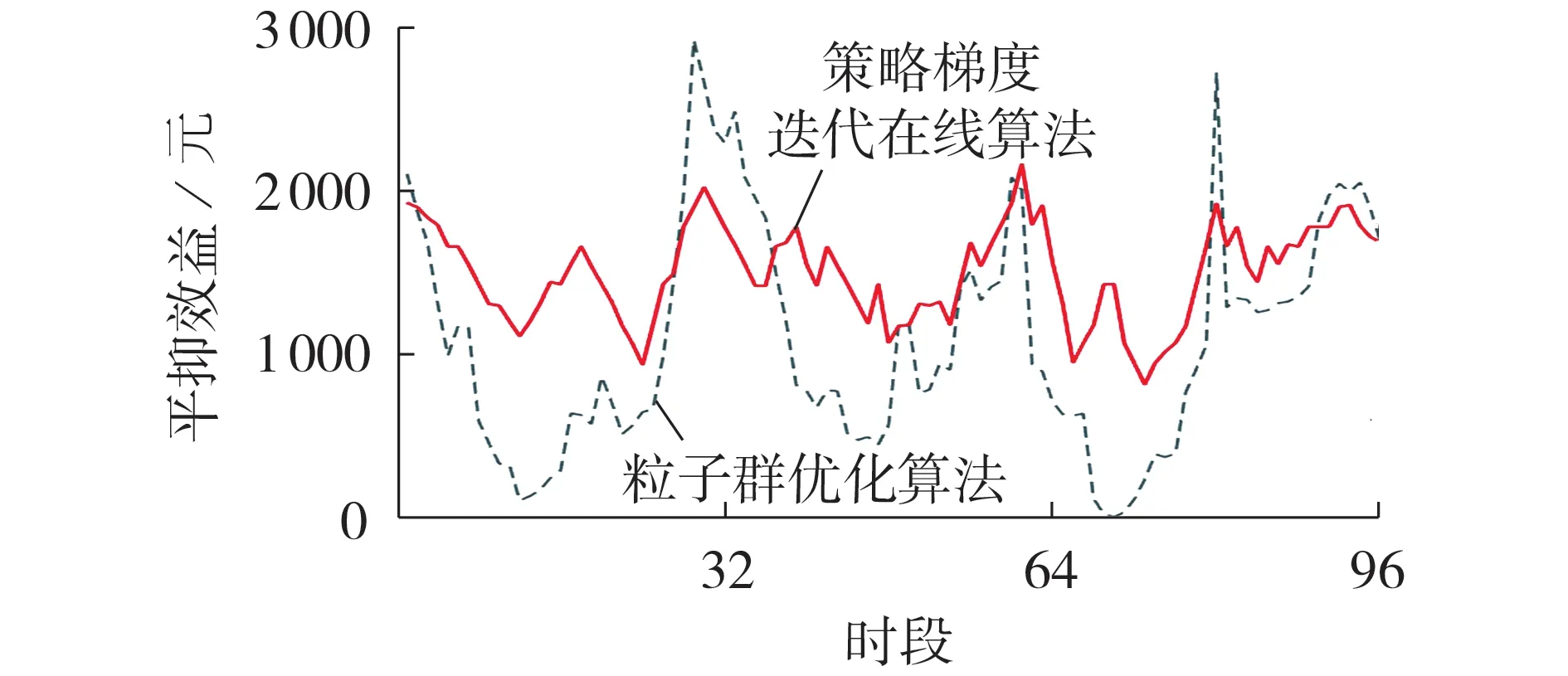
图6 不同算法下的平抑效益Fig.6 Smoothing benefits under different algorithms

图7 不同算法所得长期平均收益比较Fig.7 Comparison of long-term average return obtained by different algorithms

不同算法的迭代速度如附录A 表A2 所示。由表可知：当迭代步长为800 时，策略梯度迭代在线算法的单次迭代时间为0.582 s，系统长期平均收益为1 378.5 元／时段；粒子群优化算法的单次迭代时间为0.637 s，系统长期平均收益为1 092.8 元／时段。可以看出，策略梯度迭代在线算法不仅在平抑效益上更优，由于其事件空间小于粒子群优化算法的状态空间，提高了决策速度，因此其在迭代速度方面也快于粒子群优化算法。

4 结论

本文提出了一种风电不确定事件最优平抑控制策略，考虑到维数灾难问题与策略迭代问题，应用EBO 理论来求解最优平抑控制策略。同时，基于储能备用匹配度与辅助服务市场平抑效益构建平抑目标函数，充分挖掘电力系统内部现有各种备用资源的灵活性。基于策略梯度在线迭代算法得到最优平抑控制策略，使得“风-储-荷”联合单元在实现最优平抑效果的同时，得到最大化的平抑效益。基于算例结果可得如下结论。

1）本文以能量作为分析对象，相比于以功率作为分析对象，可以更直观地反映风电不确定事件的平抑过程，且在构建数学模型时更加简单高效。

2）本文基于EBO 理论提出了以事件为研究主体的平抑控制策略，相较于粒子群优化算法，其可以同时考虑平抑动作对当前及全时段（24 h）的影响；相较于传统的以状态为研究主体的平抑控制策略，其能够反映系统结构的性质，并在平抑效果、平抑效益、决策速度上更优。

3）所提策略梯度在线迭代算法具有相对合理的复杂度，可以很好地应用于实际。基于策略梯度在线迭代算法的策略可能无法获得绝对最优的性能，但是考虑到基于策略梯度优化的特点，只在当前可控事件的基础上做出决策，因此基于EBO 理论的风电不确定事件最优平抑控制策略可以达到最优或接近最优的性能。

附录见本刊网络版（http：//www.epae.cn）。