氯离子在混凝土中扩散效应分析的MCA模型

2023-09-11马俊军蔺鹏臻

铁道学报 2023年8期

马俊军，蔺鹏臻

(兰州交通大学土木工程学院，甘肃兰州 730070)

对于海洋等腐蚀性环境下的混凝土结构而言,由于氯离子侵蚀引起的钢筋锈蚀是导致混凝土结构发生耐久性失效的主要原因[1-2]。研究氯离子在混凝土中的扩散机理和材料组分对混凝土中氯离子侵蚀扩散的影响规律将对海洋等腐蚀性环境下混凝土结构的耐久性设计、维修和加固具有重要意义[3]。

目前,物理试验由于与实际情况最为接近,已成为国内外学者研究混凝土中氯离子扩散性能最常用的方法之一[4]。但由于试验设备、场地、条件等因素的限制,使得试验结果无法反映真实环境中结构的退化侵蚀现象[5]。而且试验研究还存在周期长、成本高、试验结果离散性大等问题。针对试验方法的局限性,文献[6-8]在Fick第二定律的基础上,通过考虑不同的影响因素提出一系列用于描述混凝土中氯离子扩散过程的预测模型。虽然这些模型能够很好地预测混凝土中氯离子的扩散行为,但都将混凝土看成一种宏观匀质材料,且模型采用的理论公式比较简单,只能考虑单一、确定性因素对氯离子扩散效应的影响,无法考虑材料组分和随机分布对氯离子扩散效应的影响[9]。为此,文献[10]从细观角度出发,将混凝土看成由砂浆、界面过渡区(Interfacial Transition Zone,ITZ)、骨料组成的三相复合材料,并利用有限元法建立用于描述氯离子在混凝土中的细观模型,并对混凝土氯离子扩散过程的影响因素进行分析。文献[11]利用有限元法研究骨料对再生骨料混凝土中氯离子扩散特性的影响。文献[12-13]将混凝土作为由砂浆和骨料组成的两相复合材料,利用有限元法对混凝土中氯离子扩散行为进行分析。文献[2,4]提出一种考虑材料非均质分布的细观化等效方法,有效解决细观材料的宏观描述,提高模型的计算效率。但这些基于细观尺度的混凝土氯离子扩散分析方法,由于网格尺寸的限制,无法考虑混凝土实际界面过渡区的尺寸,只适用于小尺度材料层面的研究,无法在整体结构中适用。

自文献[14]用元胞自动机(Cellular Automata,CA)模拟氯离子在混凝土中的扩散过程以来,大量学者[3,15-16]利用元胞自动机对混凝土氯离子扩散过程进行研究。与有限元方法相比,该方法对网格尺寸没有限制,可以根据需要随意划分网格。因此,结合细观等效化方法和CA求解方法的优点,用来解决细观模型在应用上的局限性。近来,文献[3]采用细观数值模拟方法,建立用于描述氯离子在混凝土中扩散行为的CA模型,并对元胞尺寸大小、时间步长等求解细节进行讨论和优化。

在上述研究的基础上,本文利用元胞自动机和细观尺度模拟相结合的方法对混凝土中氯离子扩散行为进行研究。利用细观尺度模拟方法建立考虑骨料等不均匀分布的混凝土随机细观模型。根据氯离子在混凝土中的实际扩散特点,推导基于细观尺度的混凝土氯离子CA演变方程,建立基于细观尺度的元胞自动机(Mesoscale Cellular Automata,MCA)模型。利用试验结果对所提出的MCA模型的正确性和描述材料变异性的能力进行验证。利用提出的模型对影响混凝土氯离子扩散特性的各个细观结构参数进行分析。

1 混凝土细观模型的建立

在细观尺度上,可将混凝土看成由砂浆、界面过渡区(ITZ)、骨料组成的三相复合材料[17-18],由于骨料形状基本不会对混凝土中氯离子扩散效应产生影响[13,19-20],因此本文骨料采用圆形。骨料粒径范围为4.75～31.50 mm,满足Fuller级配曲线。基于蒙特卡洛(Monte-Carlo,MC)方法对生成的骨料颗粒进行随机投放[18],建立考虑骨料等不均匀分布的混凝土随机细观模型,见图1。图1中,ITZ被模拟成介于骨料和砂浆之间的等厚度薄层,其厚度一般在20～100 μm之间[21],为简化研究和提高计算效率,本文取ITZ厚度为50 μm。

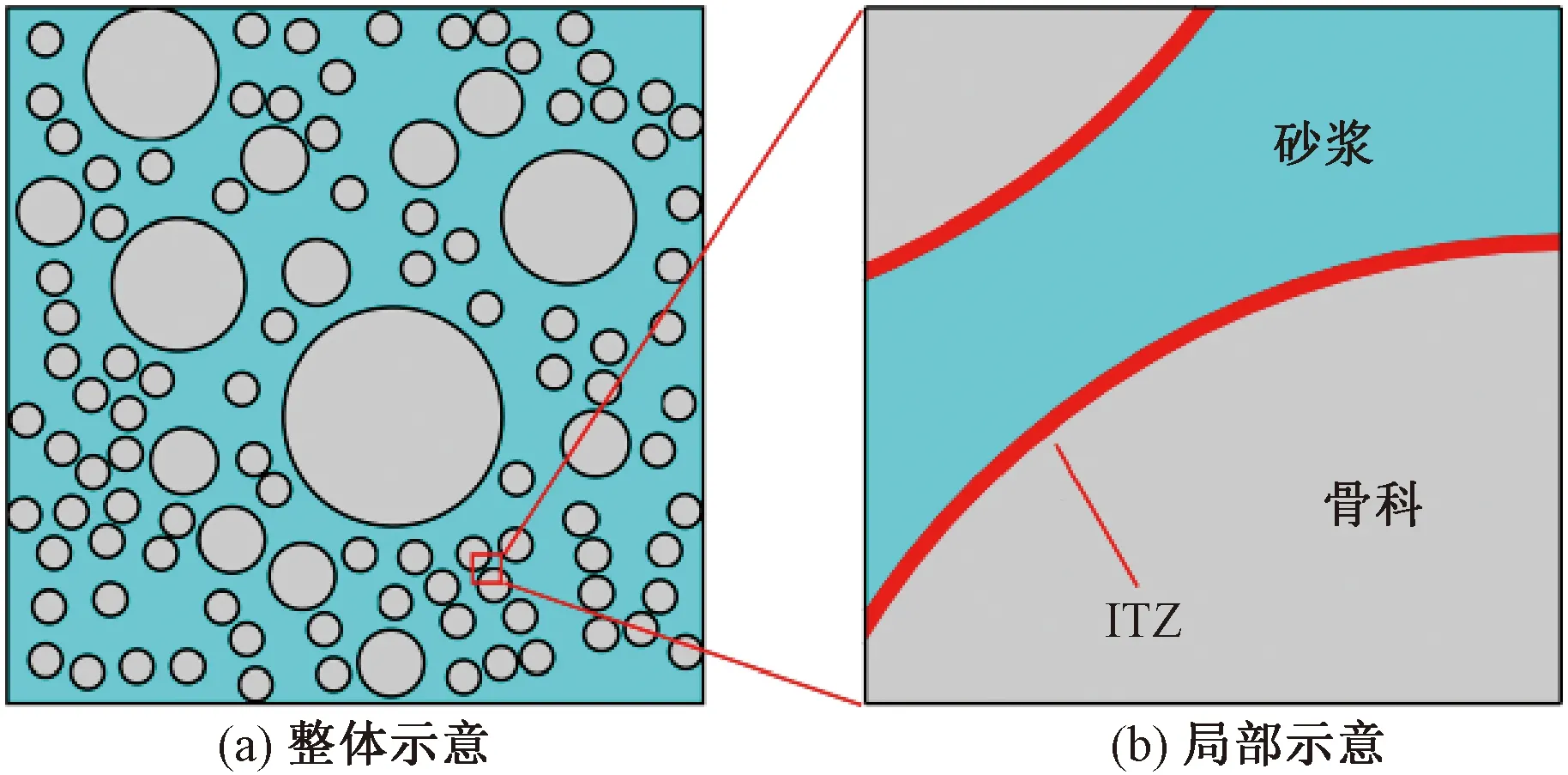
图1 混凝土细观模型示意

2 基于细观尺度的混凝土氯离子扩散过程的元胞自动机表达

元胞自动机作为一种数值计算方法,可以用来求解氯离子在混凝土中的扩散行为。在已知元胞领域类型和局部进化规则的情况下,元胞自动机局部演化方程可描述为[14-15]

S(i,t+Δt)=f[S(1,t),…,S(i,t),…,S(n,t)]

( 1 )

式中:S(i,t+ Δt)为t+Δt时刻,元胞i的状态;f为状态转移函数;n为元胞总数。

元胞C(i,j,k)各表面氯离子扩散通量示意见图2。图2中,t+ Δt时刻元胞C(i,j,k)中氯离子含量与t时刻元胞C(i,j,k)中氯离子含量和氯离子扩散通量之间的关系可描述为[3]

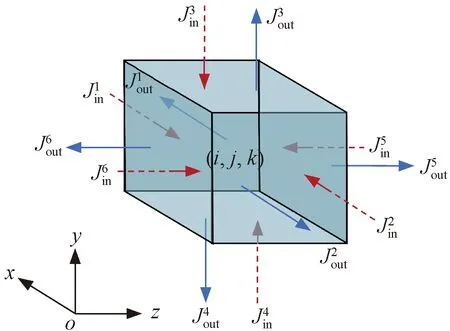
图2 元胞C(i, j, k)各表面氯离子扩散通量示意

( 2 )

式中:C(i,j,k,t)、C(i,j,k,t+ Δt)分别为t、t+ Δt时刻单元(i,j)中氯离子含量:k为混凝土中氯离子扩散沿平面坐标的4个方向;Ak为两元胞之间沿k方向氯离子扩散面的面积,m2;Jout为从元胞(i,j)流出的氯离子扩散通量;Jin为从元胞(i,j)流入的氯离子扩散通量。

二维元胞领域类型示意见图3。

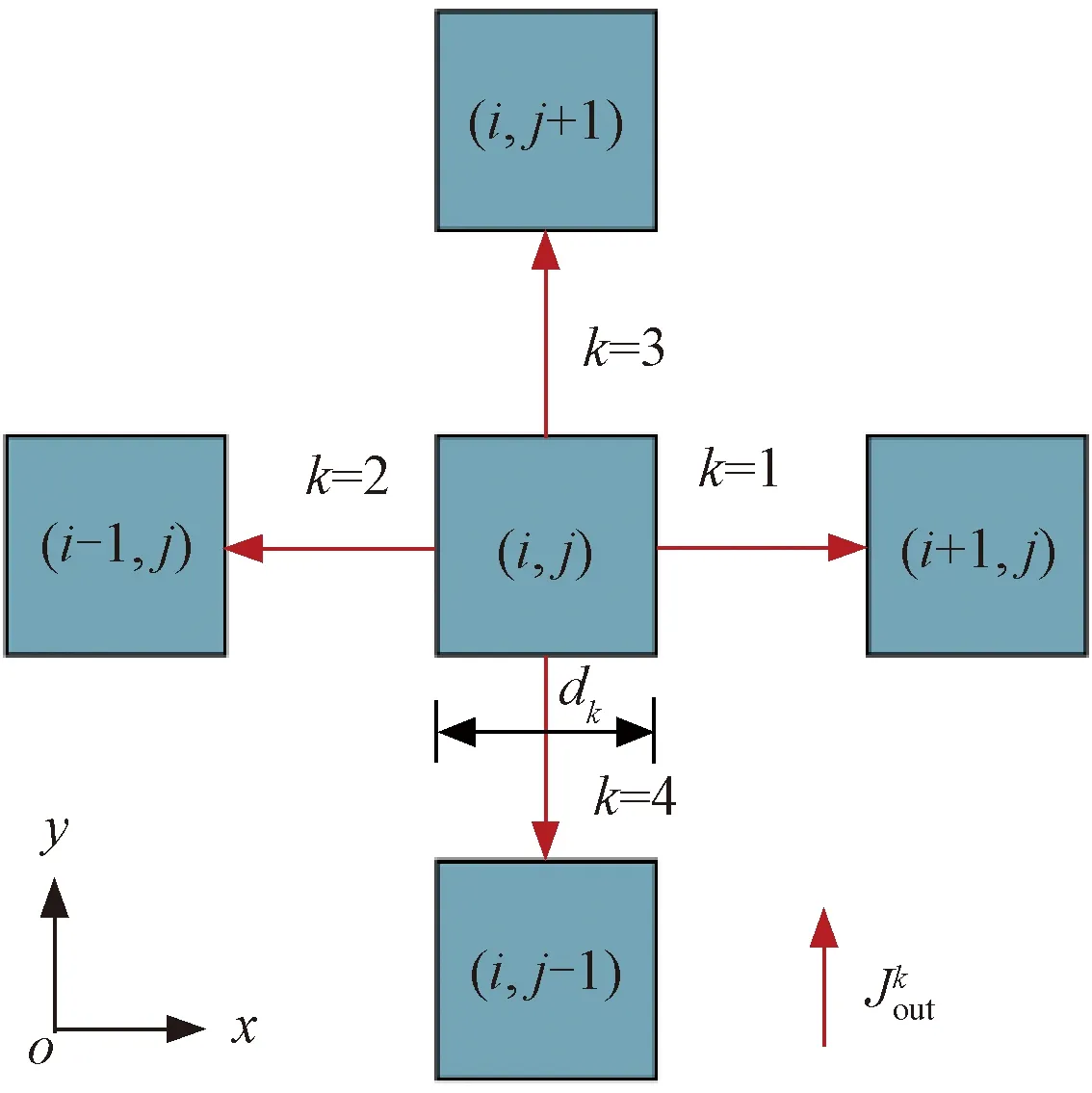
图3 二维元胞领域类型示意

对于平面模型,根据式( 1 )、图3,式( 2 )可进一步改写为

( 3 )

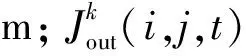
根据扩散第一定律,沿某一方向,氯离子扩散通量与其浓度成正比,即

( 4 )

式中:Dk(i,j)为元胞(i,j)沿k方向扩散到邻居元胞(i+ik,j+jk)时的氯离子扩散系数,m2/s;c(i,j,t)为t时刻元胞(i,j)氯离子浓度值,%;δk为两相邻元胞之间的中心距离,m;当k=1～4时,ik、jk的取值分别为

( 5 )

结合式( 4 ),式( 3 )可以进一步描述为

( 6 )

当采用正方形元胞时,即dk=δk=δ。其中,δ为正方形元胞尺寸。式( 6 )可以简化为

[c(i,j,t)-c(i+ik,j+jk,t)}

( 7 )

根据大数定理,元胞内氯离子含量与氯离子浓度成正比,即

C(i,j,k,t)=c(i,j,k,t)·Ae

( 8 )

式中:Ae为元胞内氯离子传输的有效面积。

此时,氯离子在混凝土中的扩散过程可以表达为

[c(i,j,t)-c(i+ik,j+jk,t)}

( 9 )

在不考虑骨料传输的情况下,即骨料中氯离子扩散系数DAgg=0,有效面积Ae可以表示为

Ae=(AMor+AITZ)δ2=(1-AAgg)δ2

(10)

式中:AMor、AITZ分别为元胞内砂浆、TTZ面积;AAgg为元胞内骨料所占的面积。

至此,式( 9 )可表达为

(11)

利用式(11)可建立混凝土中氯离子扩散过程的元胞自动机模型。

对于混凝土细观模型而言,由于骨料和界面过渡区在空间上的随机分布,使得元胞(i,j)沿任意方向表现出不同的侵蚀特性,主要体现在氯离子扩散系数Dk(i,j) 在各个方向上的取值具有随机性。因此,为便于分析这种材料随机性,本文提出一种细观等效方法来模拟材料随机性,以图1中的混凝土细观模型中的元胞(i,j)为例,其等效过程见图4。主要分为以下几个步骤:

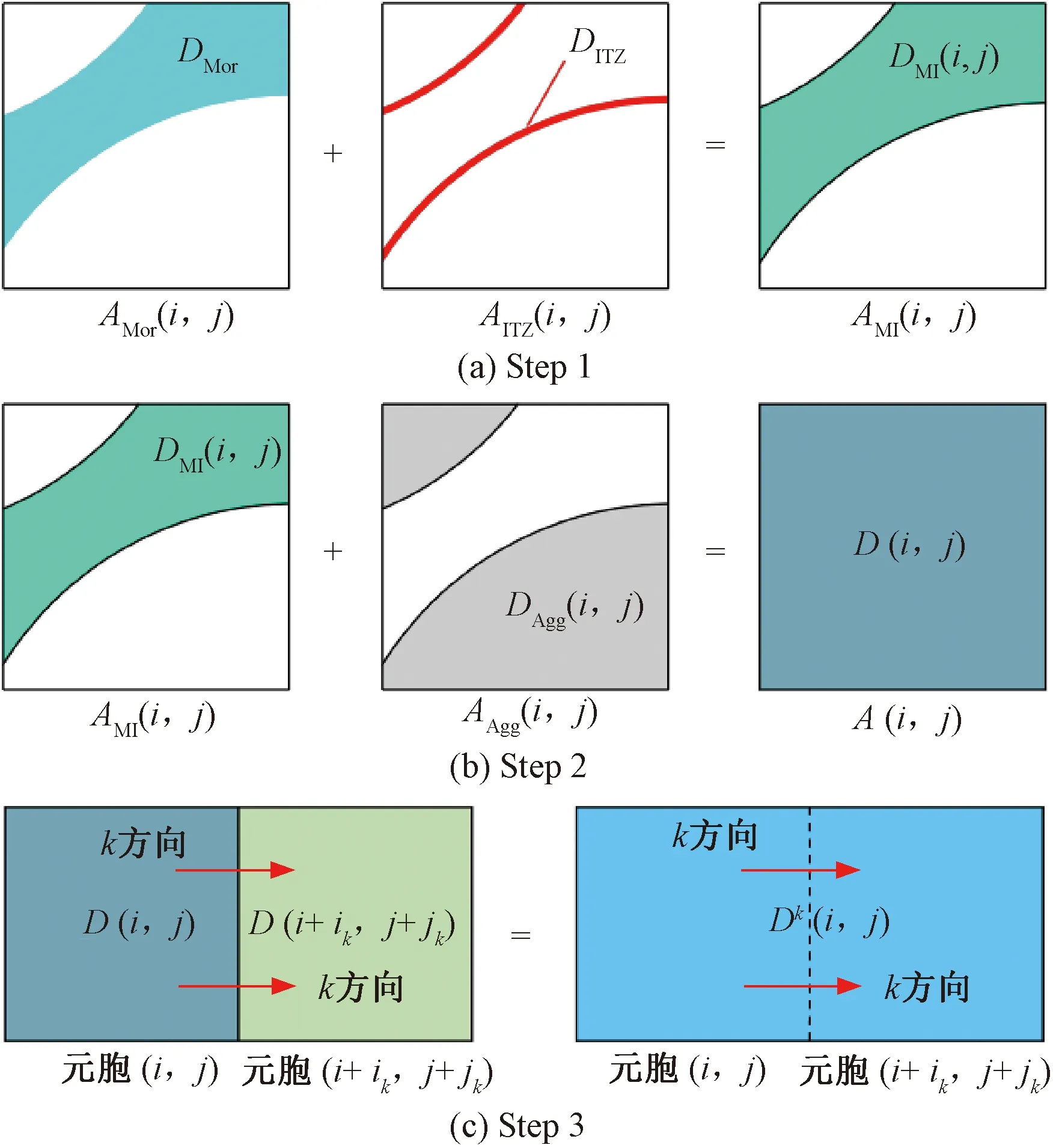
图4 细观模型等效过程示意

Step1根据元胞内砂浆、ITZ的面积分数,将元胞内砂浆、ITZ的氯离子扩散系数DMor(i,j)、DITZ(i,j)进行第一次均匀化等效,得到等效后氯离子扩散系数DMI(i,j)。

Step2根据元胞内骨料的面积分数,将Step1中等效后的氯离子扩散系数DMI(i,j)和骨料中氯离子扩散系数DAgg(i,j)进行第二次等效,得到等效后元胞氯离子扩散系数D(i,j)。

Step3根据元胞自动机局部演变规则,将上述得到的各元胞氯离子扩散系数D(i,j)沿着不同的扩散方向进行平均化处理,得到平均氯离子扩散系数Dk(i,j)。

由图4可知,等效后各元胞的氯离子扩散系数D(i,j) 可以表示为各混凝土组成成分与其氯离子扩散系数的关系式,即

(12)

式中:AITZ(i,j)、AMor(i,j)、AAgg(i,j)分别为元胞(i,j)中界面过渡区、砂浆、骨料所占的面积分数,%;DAgg为骨料中氯离子扩散系数,一般取DAgg=0;DMor为砂浆中氯离子扩散系数;DITZ为ITZ中氯离子扩散系数,其与砂浆中氯离子扩散系数DITZ存在如下关系[21-22]

DITZ=αDMor

(13)

其中,α为ITZ与砂浆中氯离子扩散系数的比值,根据文献[22],α和界面过渡区厚度tITZ之间的关系可以表示为

(14)

根据元胞内有效扩散系数D(i,j),Step3中各方向等效扩散系数Dk(i,j)表现出不同的等效结果,分别为:

(1)当D(i,j)=0或D(i+ik,j+jk)=0时,k方向扩散系数Dk(i,j)可以等效为

Dk(i,j)=0

(15)

(2)当D(i,j)≠0且D(i+ik,j+jk)≠0时,k方向扩散系数Dk(i,j) 可以等效为

(16)

3 氯离子扩散过程的时变效应

根据Thomas等[23]的试验研究,发现混凝土中氯离子扩散系数随时间t的关系可以用幂函数来表示,即

(17)

式中:DMor(t)为考虑侵蚀时间后的氯离子扩散系数,m2/s;D0为表观氯离子扩散系数,m2/s;t0为混凝土参考龄期,一般取t0=28 d;m为时间依赖性参数。

4 计算流程

按照上述提出的混凝土随机细观模型和元胞自动机模拟方法,利用Matlab软件编写混凝土氯离子扩散效应分析的细观元胞自动机模型计算程序,具体流程见图5。图5中,Ncell为元胞总个数。

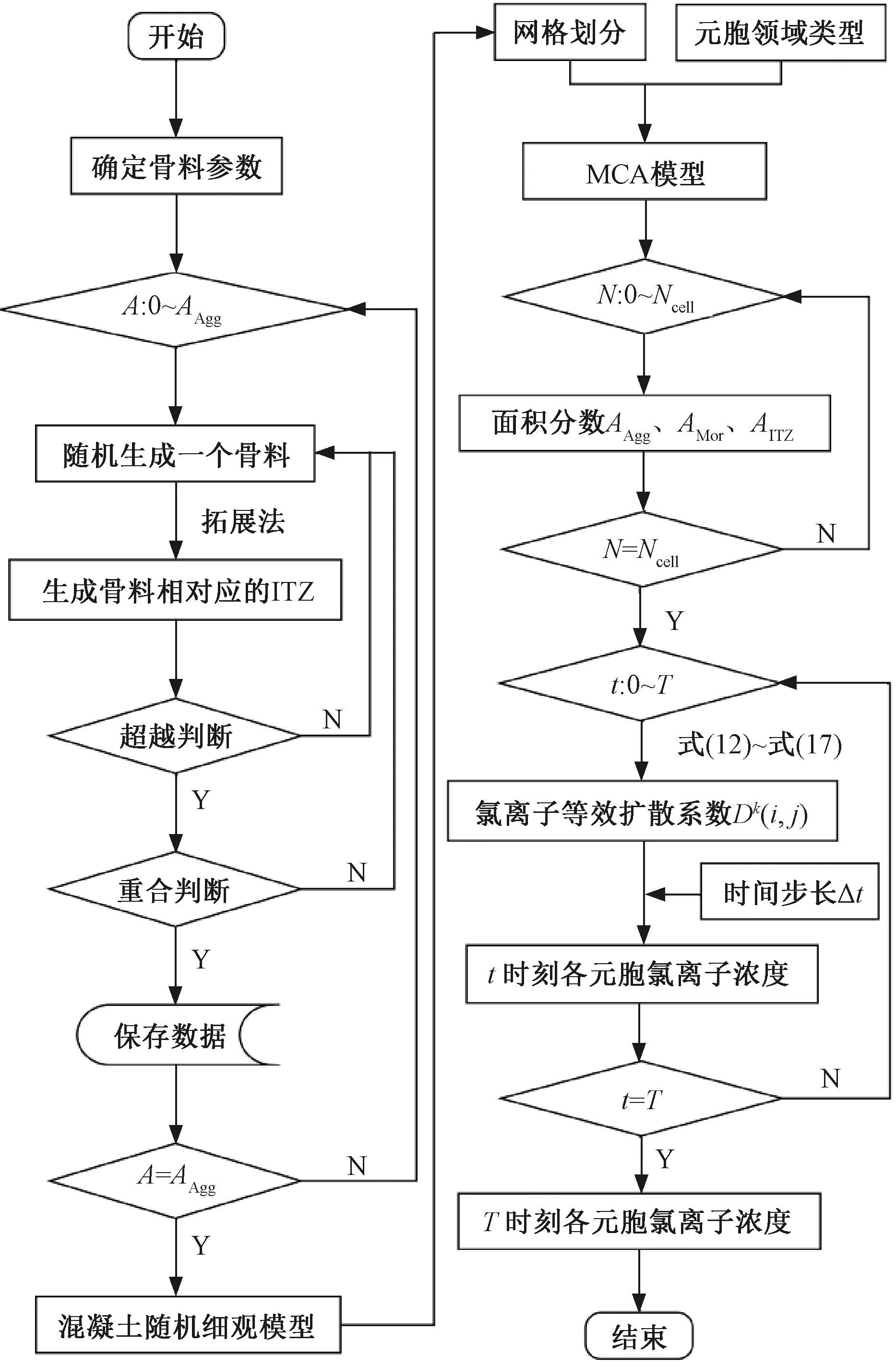
图5 混凝土氯离子扩散效应分析流程示意

5 元胞尺寸确定方法

从上述等效过程可知,元胞尺寸太大,模型无法真实反映骨料在截面内的实际分布,造成模拟值与实际结果的偏差。元胞尺寸太小,不利于混凝土细观参数的统计与提取,也降低了计算效率。根据式(10),在采用圆形骨料的情况下,为使建立的MCA模型能真实反映骨料在截面内的实际分布,理论上元胞尺寸应满足如下关系

(18)

式中:δe、δmax分别为模型计算、最大理论尺寸,当δe=δmax时,模型计算结果最准确、高效,当采用尺寸δe无法进行网格划分时,可取δe<δmax,但为保证精度,取值不易太小;dmin为骨料最小粒径,m。

为验证式(18)确定的元胞尺寸是否合理。以图1中的混凝土细观模型为例,考虑混凝土实际尺寸和元胞类型,同时为便于网格划分,利用数值试验,分别比较δ=1、2、4、5 mm时MCA模型的模拟结果。模拟历经480 d后混凝土截面氯离子浓度的分布情况,选择距离混凝土表面不同深度氯离子浓度模拟值的平均值作为评价指标,比较结果见图6。同时,为便于比较,图中还给出了宏观尺度下Fick第二定律的解析解。

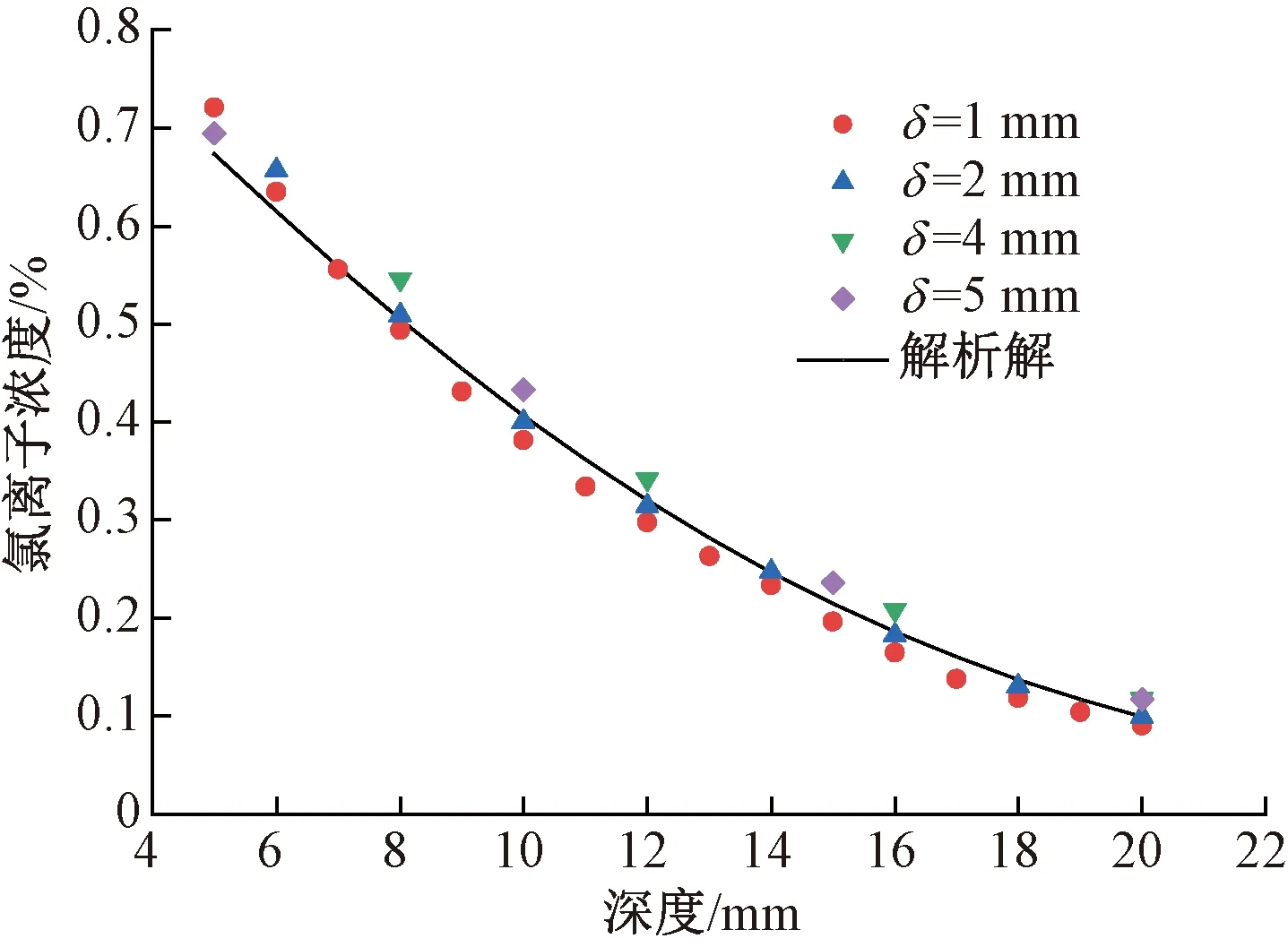
图6 不同元胞尺寸下MCA模型的模拟结果与解析解的比较

由图6可知,不同网格尺寸下,截面氯离子浓度模拟值随深度的变化规律与解析解随深度的变化规律一致。当δ=2 mm(最接近δmax=3.4 mm)时,模型模拟值与解析解之间偏差最小。当元胞尺寸太小(δ=1 mm),模型将低估氯离子在混凝土中的扩散行为。当δ>δmax,即δ=4、5 mm,模型将高估氯离子在混凝土中的扩散行为。这说明MCA模型元胞尺寸确定方法是合理的。对于常规混凝土而言,为使MCA模型计算结果高效、准确,推荐采用δ=0.707dmin。

6 数值模拟与试验验证

6.1 MCA模型的建立

为验证MCA模型的准确性,对文献[24]中强度等级为C30的混凝土受氯离子侵蚀试验过程进行数值模拟,将模型模拟结果与试验结果进行比较。根据混凝土细观尺度模拟方法,建立截面尺寸为100 mm×100 mm的混凝土细观模型,见图1。图1中,骨料面积分数(AAgg=40%)和粒径分布(4.75～31.50 mm)与文献[24]相同。为便于与试验结果进行对比,根据第4节的研究结果,在保证计算精度的情况下,δ=2 mm,划分后的混凝土随机细观模型见图7。

图7 混凝土细观模型网格划分示意

在混凝土细观模型等效时,D0=3.931×10-12m2/s,m=0.608 3,t=480 d,混凝土界面扩散特性参数利用式(14)确定,等效后各元胞等效氯离子扩散系数见图8。由图8可知,等效后截面各位置氯离子扩散系数不再是常数,而是随骨料等组成成分的变化而变化。通过与图1对比,发现颜色越接近红色代表元胞内砂浆的面积分数越高,等效后D0越大;颜色越接近蓝色代表元胞内AITZ越高,等效后D0越小。说明提出的氯离子扩散系数等效方法可以模拟混凝土中骨料和ITZ随机分布对D0的影响。

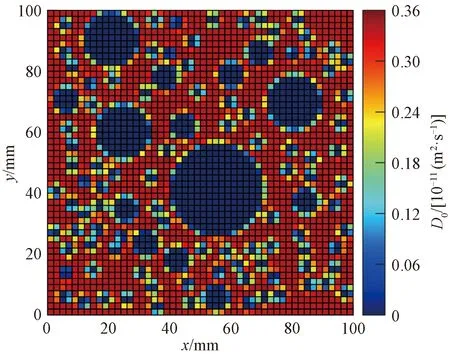
图8 等效氯离子扩散系数分布

6.2 氯离子浓度验证

为验证MCA模型的准确性,将模型的模拟结果与文献[24]中试验结果进行比较。由于基于化学滴定法得到的氯离子浓度实测值代表的是截面氯离子浓度分布的平均结果,因此为便于与试验结果进行比较,选择距离混凝土表面同一深度氯离子浓度模拟值的平均值作为评价指标。模型计算参数分别为:D0=3.931×10-12m2/s,实际氯离子扩散系数根据式(12)～式(16)确定,m=0.608 3,Δt=0.1 d,δ=2 mm。不同侵蚀时间后截面平均氯离子浓度模拟值和试验实测值随深度h、时间的变化曲线见图9。

由图9可知,模型的模拟结果与试验值随侵蚀深度和时间的变化趋势一致,均随侵蚀深度的增加而减小,随侵蚀时间的增加而增加。表明利用MCA模型预测的氯离子浓度随侵蚀深度和时间的变化规律与试验结果一致。

随后,将MCA模型预测的截面氯离子浓度模拟值与文献[24]中实测值进行对比,对比结果见图10。由图10可知,除少数氯离子浓度模拟值与实测值之间的偏差在35%以内,所有采用MCA模型模拟的截面氯离子浓度模拟值与实测结果之间的偏差都在±10%以内。说明提出的模型可以用于模拟氯离子在混凝土中的扩散过程,且精度较高,这也可以通过图6中模型模拟值与解析解的偏差得出。通过与文献[24]对比,发现造成极少数氯离子浓度模拟值与试验值偏差的主要原因是模型采用的氯离子扩散系数是文献[24]通过试验数据拟合后的结果,而文献[24]中的试验数据来自不同的试验环境,试验数据的采集也来自不同测试人员,使得各试验数据之间本身存在一定的误差。

图10 氯离子浓度实测值与模拟值的对比

6.3 空间变异性验证

与传统有限元细观模型相比,MCA模型除能准确描述混凝土截面平均氯离子浓度随时间和深度的变化外,还应能描述材料变异特性,如骨料尺寸大小、空间不均匀分布等对氯离子扩散行为的影响。为此,在上述分析的基础上,利用MCA模型给出不同侵蚀时间后截面氯离子浓度分布示意,见图11。

由图11可知,在同一侵蚀时刻,距离混凝土表面同一深度氯离子浓度值各不相同,在砂浆分布区域(颜色越接近红色区域),元胞代表的氯离子浓度最大,在骨料分布区域(颜色越接近蓝色区域),元胞代表的氯离子浓度最小,这与氯离子在混凝土中的实际扩散行为相符,即氯离子扩散行为仅发生在砂浆区域,而不考虑骨料的渗透性。说明提出的氯离子扩散系数等效方法是合理的,也证明模型具有描述材料变异特性的能力。

在应用方面,由于MCA模型在求解过程中不需要求解高阶微分方程,因此可模拟任意复杂结构中氯离子的扩散行为。利用MCA模型,可以使工程设计人员直观了解混凝土截面内最容易引起钢筋锈蚀的薄弱位置,进而对结构的耐久性设计、寿命预测、维修和加固等提供一定的理论依据。

此外,从计算效率来看,当δ=2 mm时,MCA模型所需的元胞数量仅为50个,远远小于传统有限元细观模型所需的单元数[2],相比而言,MCA模型大大提高了模型的计算效率。

7 参数分析

在上述对模型的准确性进行验证的情况下,利用MCA模型进行敏感性分析,以验证骨料分布形式、骨料含量、界面扩散特性等细观结构参数对氯离子扩散效应的影响。纯砂浆截面见图12(a)。为便于讨论,将纯砂浆截面中氯离子浓度值作为参考,以此来验证各细观参数对氯离子宏观扩散特性的影响程度。同时为反映各细观结构参数对氯离子扩散的影响规律,引入截面有效氯离子扩散系数平均值Da,其表达式为

图12 不同骨料分布形式的混凝土细观模型和砂浆模型示意

(19)

式中:D(i,j)为各元胞的氯离子扩散系数,m2/s;m、n分别为截面内元胞的行数、列数。

7.1 骨料分布形式

为研究骨料分布形式对混凝土氯离子扩散效应的影响,考虑骨料在混凝土中的随机分布,建立5种不同骨料分布形式的混凝土细观模型,见图12(b)～图12(f),截面尺寸为100 mm×100 mm。利用MCA模型对5种不同骨料分布形式下混凝土中氯离子扩散过程进行数值模拟,计算参数分别取:Δt=0.1 d,t=480 d,m=0.608 3,D0=3.931×10-12m2/s,实际氯离子扩散系数根据式(12)～式(16)确定,AAgg=0.4,tITZ=50 μm,δ= 2 mm。

截面有效氯离子扩散系数平均值Da随骨料分布形式的变化关系见图13。由图13可知,不同骨料分布形式下Da基本保持不变。说明骨料分布形式基本不会对混凝土中氯离子宏观分布规律产生影响。

图13 Da随骨料分布形式的变化关系

同时,为便于同其他细观参数比较,选择距离混凝土表面同一深度氯离子浓度平均值作为评价指标。不同骨料分布形式下截面氯离子浓度模拟值与参考值的比较结果见图14。由图14可知,截面各模拟值与参考值之间最大偏差不超过12%。说明在一定误差范围内,可认为骨料分布形式基本不会对截面氯离子浓度分布规律产生影响,这与图13得出的结论一致。

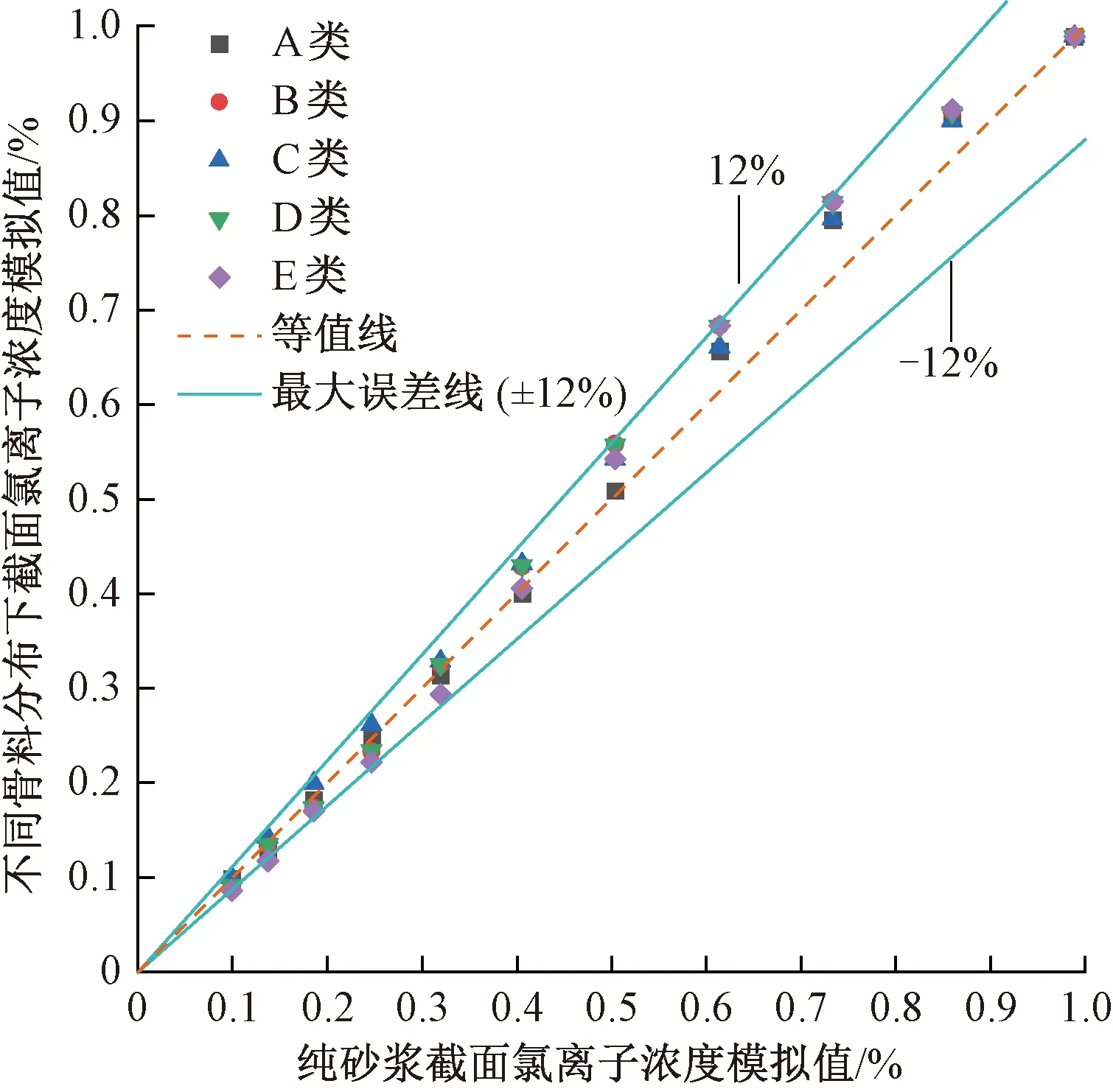
图14 不同骨料分布形式下截面内氯离子浓度模拟值与参考值的比较结果

7.2 骨料含量

为研究骨料含量对氯离子宏观扩散效应的影响,对5种不同骨料含量下混凝土中氯离子侵蚀过程进行模拟,除AAgg外,各计算参数、模型尺寸均与上述模型保持一致。截面有效氯离子扩散系数平均值Da随骨料含量AAgg的变化曲线见图15。

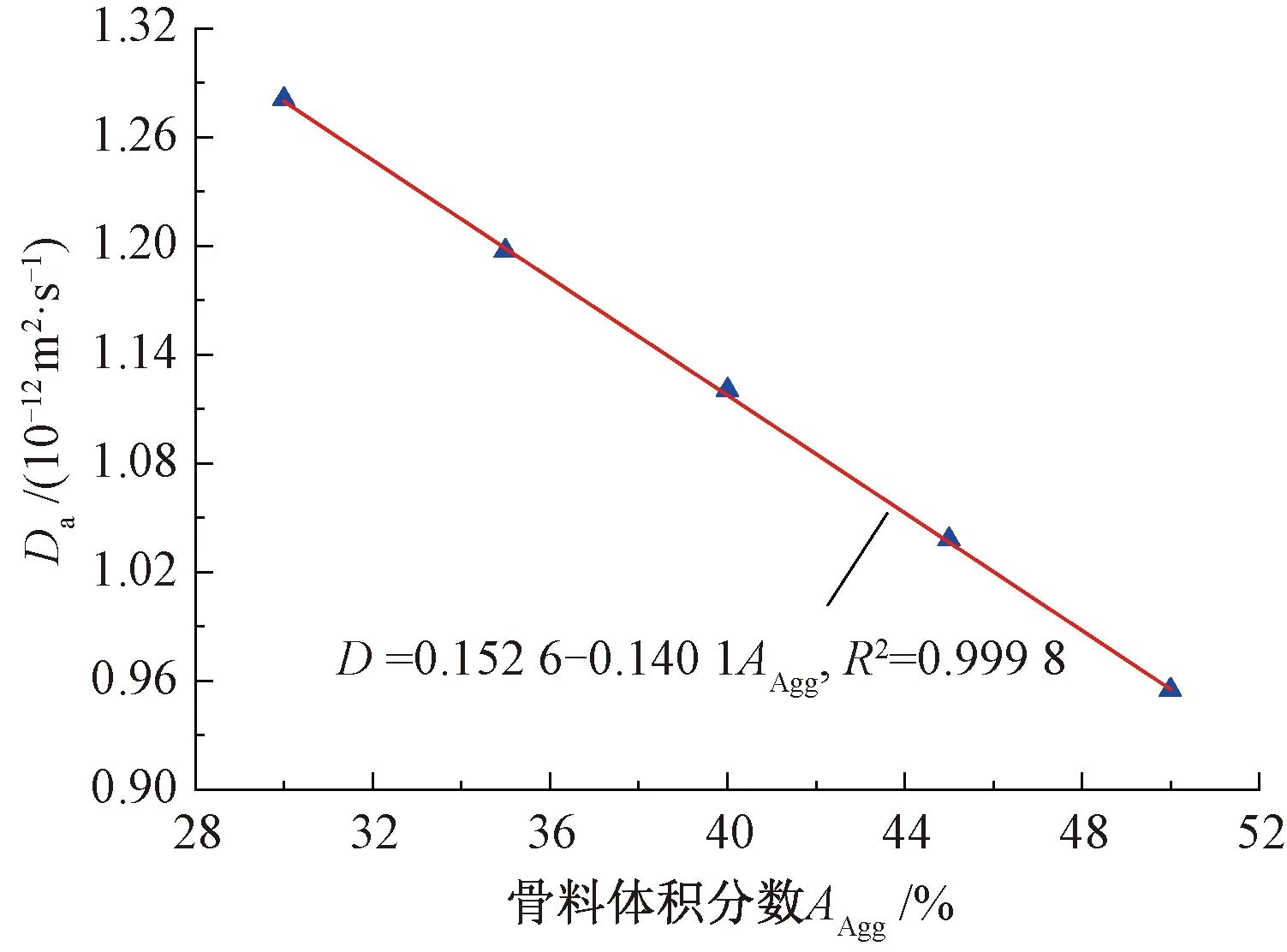
图15 Da随AAgg的变化曲线

由图15可知,随着骨料含量的增加,Da呈现出线性减小的变化规律。结果表明,随着AAgg的增加,氯离子在混凝土中的宏观扩散特性逐渐减弱,增加混凝土中骨料的含量可以抑制氯离子在混凝土中的扩散行为。同时,为便于同其他细观结构参数进行比较,选择距离混凝土表面同一深度氯离子浓度模拟值的平均值作为评价指标,将上述氯离子浓度模拟值与其平均值进行对比,见图16。

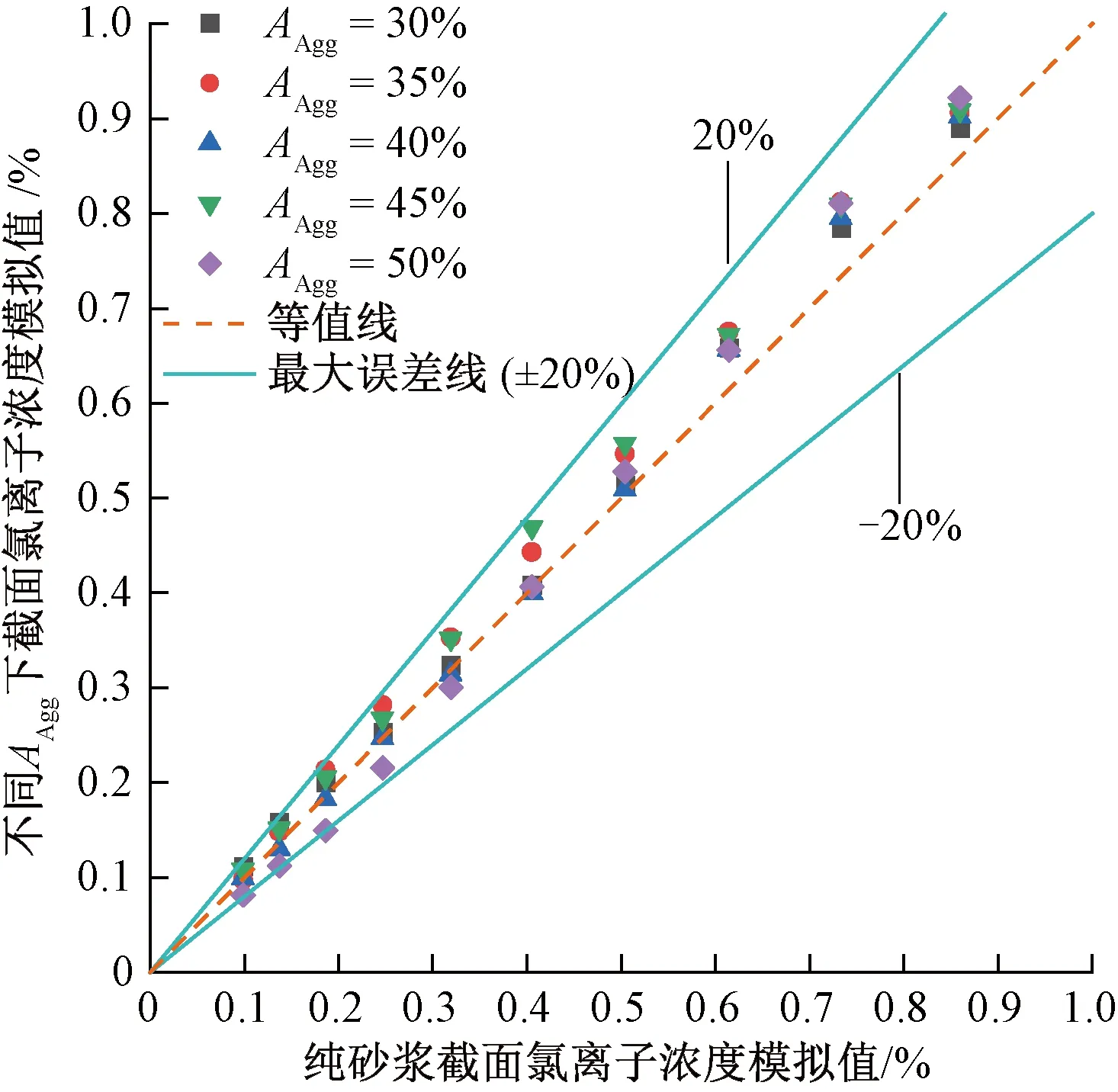
图16 不同AAgg下截面内氯离子浓度模拟值与参考值的比较

由图16可知,截面各位置氯离子浓度模拟值与参考值之间最大误差为20%,截面各位置氯离子浓度模拟值与参考值之间的偏差随氯离子浓度值的增加而减小。

7.3 界面扩散特性

ITZ作为连接骨料和砂浆的重要组成成分,是混凝土中最为薄弱的部位,也是影响混凝土结构力学性能和耐久性的主要因素。因此,为研究混凝土界面扩散特性对氯离子扩散效应的影响,对8种不同α(DITZ/DMor)下混凝土中氯离子侵蚀过程进行模拟。除α外,各计算参数、模型尺寸均与上述模型保持一致。截面有效氯离子扩散系数平均值Da随α的变化曲线见图17。

图17 Da随 α的变化曲线

由图17可知,Da随α的增加呈现出线性增加的变化规律。结果表明,随着α的增加,氯离子在混凝土中的宏观扩散特性逐渐增强。

同时,为便于同其他参数进行对比,选择距离混凝土表面同一深度氯离子浓度平均值作为评价指标,将上述不同α下截面氯离子浓度模拟值与参考值进行比较,结果见图18。

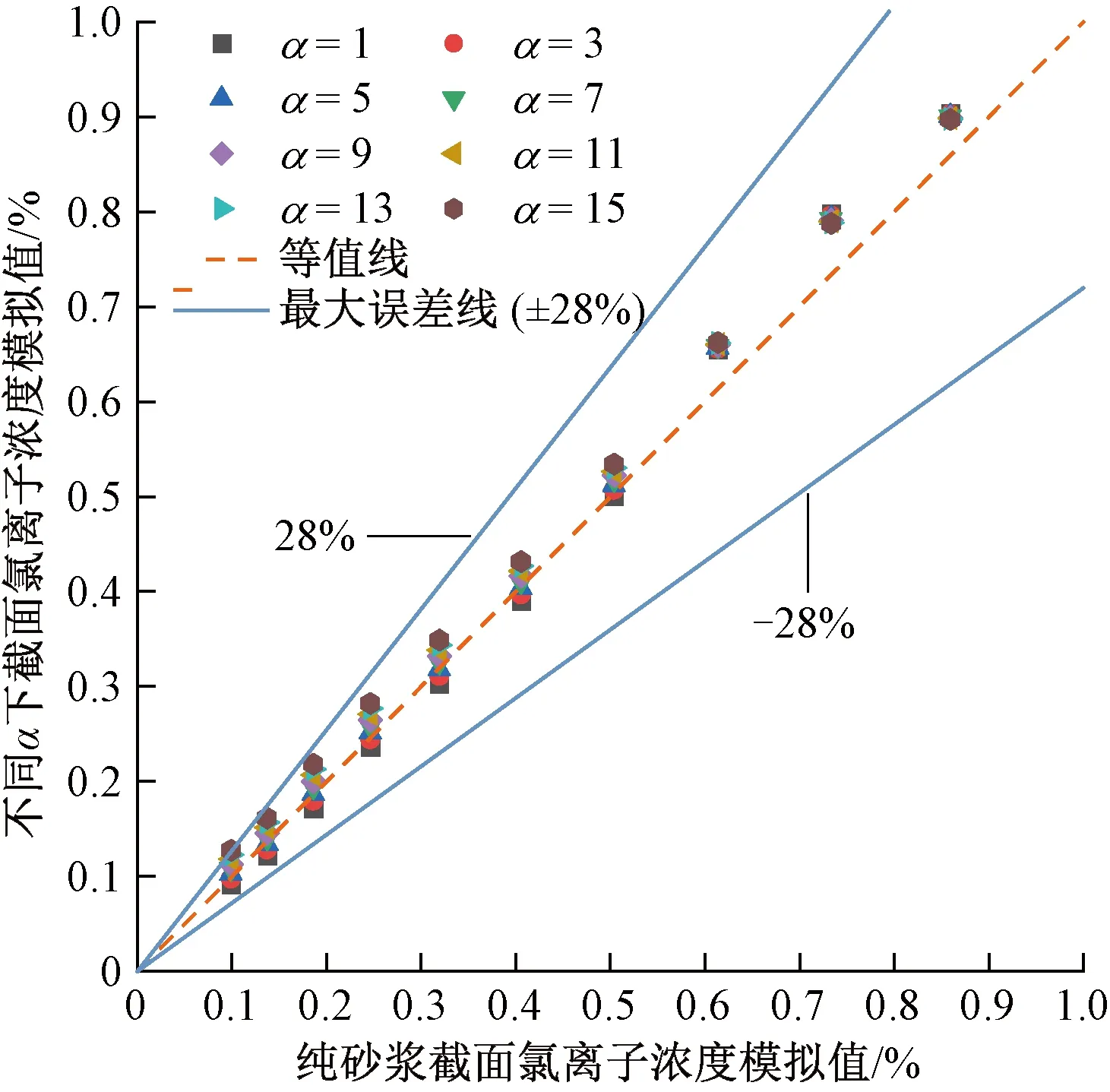
图18 不同α下截面内氯离子浓度模拟值与参考值的对比结果

由图18可知,不同α下截面氯离子浓度模拟值之间的差值随氯离子浓度的减小而增加。当α=15时,两者之间偏差最大,为28%。可见α的取值对氯离子在混凝土中的宏观扩散特性存在很大的影响,在氯离子扩散效应分析时,合理选择α值将直接关乎结果的正确与否。

综上所述,通过对比不同参数下截面中氯离子浓度模拟值与参考值之间的偏差,发现界面扩散特性对细观混凝土中氯离子的宏观扩散特性影响最显著,两者之间偏差最大,为28%,体积分数对细观混凝土中氯离子的宏观扩散特性影响较为显著,两者之间偏差为20%,而骨料分布形式则基本不会对混凝土氯离子扩散效应产生影响,两者之间偏差最小,仅为14%,这与既有研究结果规律一致[13,19-20]。