高频循环荷载作用下砂土抗剪强度试验研究

陕 耀，陈 平，3，周顺华，叶伟涛，代 宁

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.上海市轨道交通结构耐久与系统安全重点实验室，上海 201804；3.中铁城市发展投资集团有限公司，四川 成都 610218)

颗粒土常受车辆交通振动、地震、爆破、施工作业、机械振动等的影响。例如,高速列车的振动会导致路基局部沉降甚至破坏,严重影响高速列车运行的平稳性和行车安全性[1-3]。当车速从350 km/h提高至400 km/h,甚至再往上突破时,由高频振动所引发的路基土体动力学问题将会愈加突出。列车振动引起的弹性波在土体内扩散和传播,会导致土体颗粒间的摩阻力下降,从而导致土体产生显著变形并影响上部以及邻近结构[4-10]。目前,车致高频循环荷载作用所引起的轨下基础散体材料的物理力学机制,尤其是土体的强度变化尚不明确。因此,通过高频循环振动下的散体材料力学行为的研究,可以对高铁路基的局部破坏和沉降中颗粒土的受力和变形特性产生新的认识。振动中颗粒土的强度不仅取决于振动特性,如加速度、频率和振幅,还与颗粒土的物理性质,如含水量、粒度分布、颗粒形状、相对密度或孔隙比、颗粒土的黏聚力和内摩擦角等因素有关。除此之外,散体材料的振动特性在地震、振动流化床以及其它物理力学领域也存在相应的问题[11-22],国内外学者采用室内模型试验、动直剪试验和动三轴试验等手段,研究了振动作用对颗粒材料尤其是砂土强度特性的影响。

Barkan[11]通过改进的动直剪仪研究了水平振动对砂土抗剪强度参数的影响,研究表明,振动强度是决定砂土内摩擦角和孔隙率大小的主要参数,并且砂土的内摩擦角和孔隙率都随振动强度的增大而不断减小。Grossman[12]认为振动会引起颗粒材料的流动,并将其归因于颗粒和界面之间的非弹性摩擦作用。Aumaitre等[13]研究了颗粒材料在正弦振动下的力学行为,结果表明加速度对颗粒运动状态影响较大。Raihane等[22]的试验结果证实了文献[13]的研究结论。Johnson等[14-15]对玻璃微珠开展了振动直剪试验,发现高频振动会引起颗粒材料结构的破坏,导致剪切应力下降。Denies等[16-17]发现振动会导致砂土抗剪强度显著降低,并将砂土的运动分为3类:当垂直振动的加速度幅值小于1g时,砂土表现为振动压缩;当加速度幅值接近1g时,砂土自由表面的颗粒产生流动;当加速度幅值大于1g时,砂土会发生对流和分层。

最近,文献[18-19]通过改进的动直剪试验发现结构面的粗糙度对砂土试样强度有显著影响。此外,Taslagyan等[20-21]通过改进动直剪仪研究了一系列不同正应力下振动强度对干砂抗剪强度的影响,统计了砂土在剪切作用下的峰值、残余和振动残余强度,结果表明:振动强度的增大有效降低了颗粒材料在峰值和残余状态下的内摩擦角。但由于直剪试验难以真实地反映三轴应力状态下振动对砂土抗剪强度的影响,且砂土在残余剪切强度下,各影响因素(如振动强度、有效围压、初始相对密实度、含水率和振动频率等)对砂土残余抗剪强度指标的影响,未发现有相关文献展开研究。因此,本文采用自主研制的静载与高频循环荷载耦合作用三轴仪[23-24],以国内常见的福建平潭标准砂为研究对象,对砂土在振动条件下的残余抗剪强度损失展开研究,分析振动强度、有效围压、初始相对密实度以及含水率和振动频率等因素对砂土残余抗剪强度损失的影响,探索砂土在高频循环荷载作用下的力学特性。

1 试验装置

试验采用可以施加高频循环荷载的三轴仪,系统构成主要包括:加载系统、控制系统、测量和数据采集系统,以及围压控制系统。试验装置见图1。

图1 试验装置

静力加载系统类似常规静力三轴仪的结构,以恒定的轴向应变速率加载。静力加载系统包括下部加载控制台、试样底座、反力架、围压控制系统,动力加载系统主要包括音圈电机、传力杆。音圈电机安装在荷载传感器和试样之间,振子受电流驱动,产生安培力,其振动方向为试样同轴方向。控制系统采用音圈电机驱动器,包括直流电源、精密信号发生器和功率放大器。测量和数据采集系统包括静荷载传感器、动荷载传感器、激光位移传感器、加速度传感器、动力测试分析系统。动荷载传感器用来测量振动过程中动应力幅值,加速度传感器用来测量试验振动过程中加速度幅值。动荷载传感器与加速度传感器的采集频率均为500 Hz。激光位移传感器采集频率可达2 000 Hz,记录振动过程中试样的位移幅值以及由振动引起试样的压缩变形情况。所有传感器都连接到一个动力测试分析系统,来分析加速度、轴向位移以及动应力的响应情况。试验系统相关介绍和可靠性见文献[23-24]。

2 试验材料与方法

2.1 试样材料

本文试验对象为通用的福建平潭标准砂,其颗粒级配曲线见图2。由图2可知,试验所用平潭标准砂为中砂。平潭砂的基本物理指标和颗粒形状分别见表1、图3。

表1 平潭标准砂基本物理指标

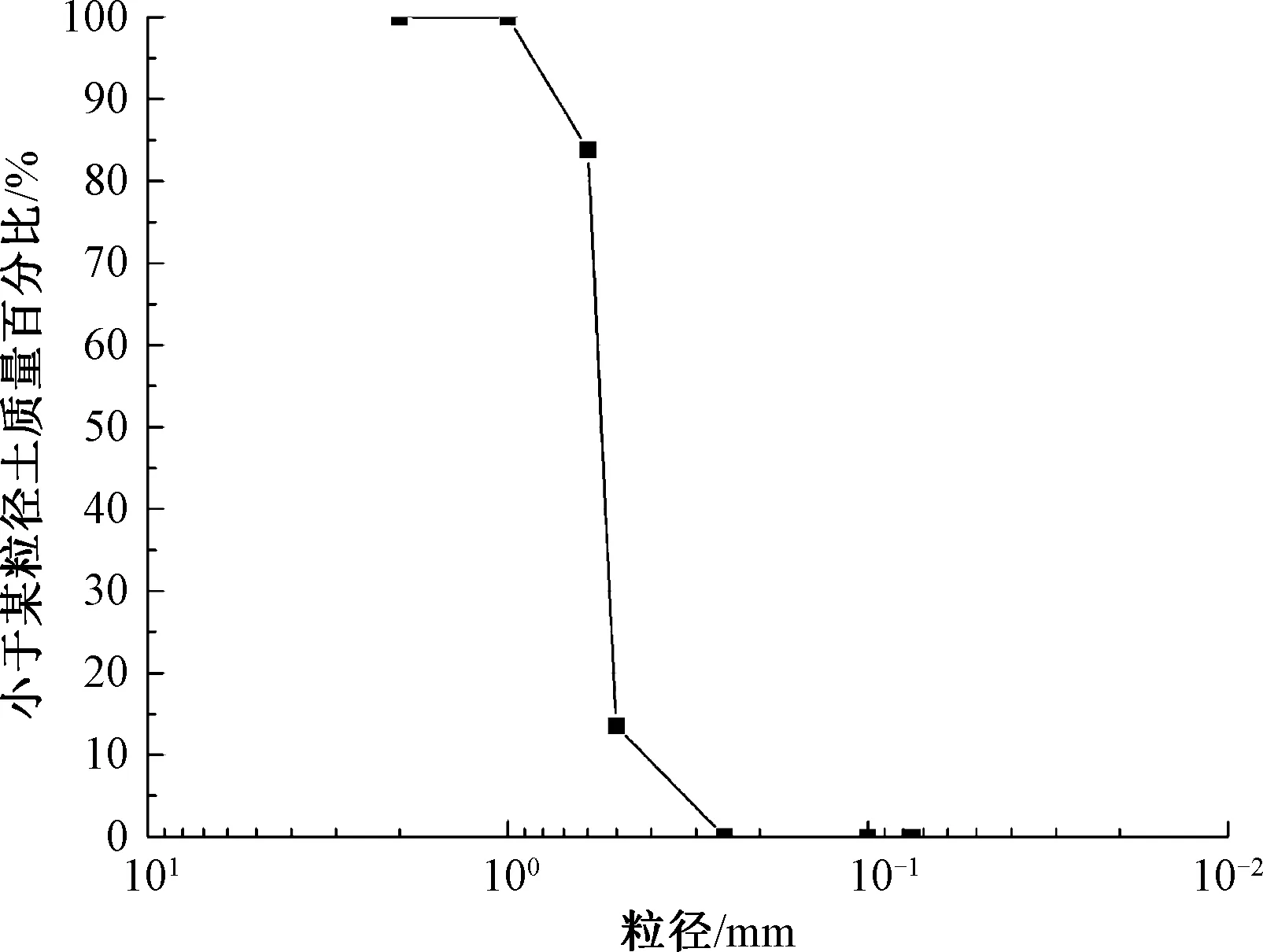
图2 颗粒级配曲线[23]

图3 平潭砂颗粒形状[23]

2.2 试样制备

三轴试样为圆柱形,尺寸为50 mm×100 mm(D×H),干砂试样采用干法制备[25]。制样时,试样通过分层压实至所需密度,当每层加至预定高度,通过小锤轻轻敲击对开模外壁使试样表面平整。制样结束后,通过给试样内部施加负压保证试样保持原状。饱和砂土试样采用湿法制备。制样前,用无气水覆盖砂土并煮沸,使砂土内空气完全排尽。待其冷却后,按文献[23]制备饱和砂土试样。当加砂完成时,通过轻轻敲击对开模使砂土试样达到指定高度,以控制饱和试样初始相对密实度。值得注意的是,加砂过程需保证砂土始终位于液面以下,从而减少空气进入,提高饱和度。当试样装载至三轴仪后,采用反压饱和法使试样完全饱和。通过反压控制方式施加加压,为了保证试样充分饱和,反压从0 kPa逐级加载至100 kPa,以溶解水中的滞留空气,直到Skempton B值不小于0.96,即试样达到完全饱和。在试样饱和的过程中,试样的有效应力不得低于10 kPa,以防止试样发生变形甚至塌陷。试样在100 kPa的有效固结围压下直至没有额外的体积变形即完成固结。饱和砂试样制备方法见图4。

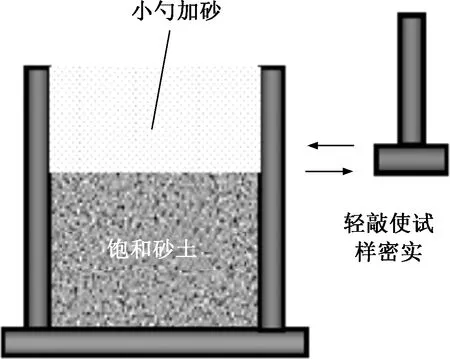
图4 饱和砂试样制备方法[23]

2.3 试验方法

试验采用应变控制模式,试样首先以恒定剪切速率v=0.1 mm/min进行单调剪切,直至试样接近临界状态。再通过音圈电机对试样施加一定时间的动荷载,加载频率和能量通过计算机端控制。试验过程中,砂土的加速度、应力和应变分别通过加速度传感器、动荷载传感器和位移传感器采集。试验加载示意见图5。

图5 试验加载示意

由图5可知,随着单调加载的进行,偏应力逐渐恢复至振动前的应力水平,再重复前述加载步骤。然而,试样轴向应变越大,试样内部各向异性越明显,此时试样与进入临界状态初期时的性质差异显著,从而试验结果差异较大。为避免因试样充分剪切使得轴向应变过大而影响试验结果,本文试验的最终轴向应变不超过15%。

Zhai等[26]通过现场实测发现京沪高铁路基土体的高频成分主要集中于20～60 Hz。为反映振动高频成分的影响,在研究加速度与抗剪强度损失的关系时,选取60 Hz作为试验的加载频率。Dai等[23]的试验结果表明,振动时间(10～30 s)对偏应力降低的影响不大,故本试验选择的振动时长为10 s。由于土体性质受众多因素的影响,本文还考虑不同初始相对密实度、有效围压、含水率、振动频率等因素对砂土在高频循环荷载作用下的力学特性的影响,试验方案见表2。

表2 试验方案

3 试验结果分析

根据无黏性土库伦公式τ=σtanφ,其中,τ为静力剪切的剪切力;σ为正应力;内摩擦角φ为强度指标,强度损失体现为内摩擦角减小。故本文确定研究对象为内摩擦角减小值,以反映强度损失状况。

采用有效应力法计算振动前砂土的内摩擦角,通过有效围压σ′分别为30、50、70 kPa条件下的静三轴试验,得到平潭标准砂的应力-应变关系。当试样剪切至残余应力状态时,基于偏应力与有效围压可计算得到轴向应力,最终得到莫尔应力圆和残余抗剪强度包络线,干砂与饱和砂的残余抗剪强度包络线见图6。由图6可知,当Dr=0.4时,干砂的残余内摩擦角φ1=36.66°;当Dr=0.7时,干砂的残余内摩擦角φ2= 36.44°;当Dr=0.4时,饱和砂土的残余内摩擦角φ3= 37.88°;当Dr=0.7时,饱和砂土的残余内摩擦角φ4= 38.39°。

图6 三轴试验不同Dr残余抗剪强度包络线

干砂在Dr=0.7、σ′3= 50 kPa时的偏应力、竖向加速度与加载时间的关系曲线见图7。当试样经历单调剪切至残余应力状态时,对试样施加正弦荷载。振动强度通常用无量纲加速度a/g表示,其中,a为振动加速度;g为重力加速度。

由图7可知,当Dr=0.7、σ′3= 50 kPa的干砂试样单调剪切至残余应力状态时,对试样施加60 Hz循环荷载,试样很快发生强度损失。而随着振动持续,干砂试样强度基本保持不变。当振动停止后,随着单调剪切继续发展,试样强度逐渐恢复至振前水平。即施加的高频循环荷载对干砂试样振动前后的抗剪强度没有长期影响,甚至还可能产生轻微的应力硬化(振后的强度比振前的强度更高)。然而,振动确实降低了试样的抗剪强度,因此,把振动达到稳定状态时试样的残余抗剪强度称为振动残余抗剪强度,对应的砂土内摩

擦角称为振动残余内摩擦角[18,21]。振动过程中产生的剪切力τ的表达式为

τ=σtanφdi

( 1 )

Δφi=φi-φdi

( 2 )

式中:φi为振动前的砂土内摩擦角值,i=1,2,3,4;φdi为振动稳定时的砂土内摩擦角值;Δφi为振动前与振动稳定时砂土内摩擦角的差值,即砂土单调剪切内摩擦角与振动残余内摩擦角的差值。为便于单位统一,将内摩擦角的减小进行归一化处理,从而定义新的变量Δφi/φi为内摩擦角降比,以更好地反映砂土内摩擦角衰减比例,也间接反映残余抗剪强度损失比例。由于饱和砂土试验现象与干砂土相似,在此不再另行展示。

3.1 振动加速度对砂土残余内摩擦角降比的影响

在60 Hz循环荷载作用下,干砂和饱和砂残余内摩擦角降比与无量纲加速度a/g的关系见图8。当单调剪切至残余应力状态时,砂土抗剪强度不会因加载的持续而发生较大的变化。

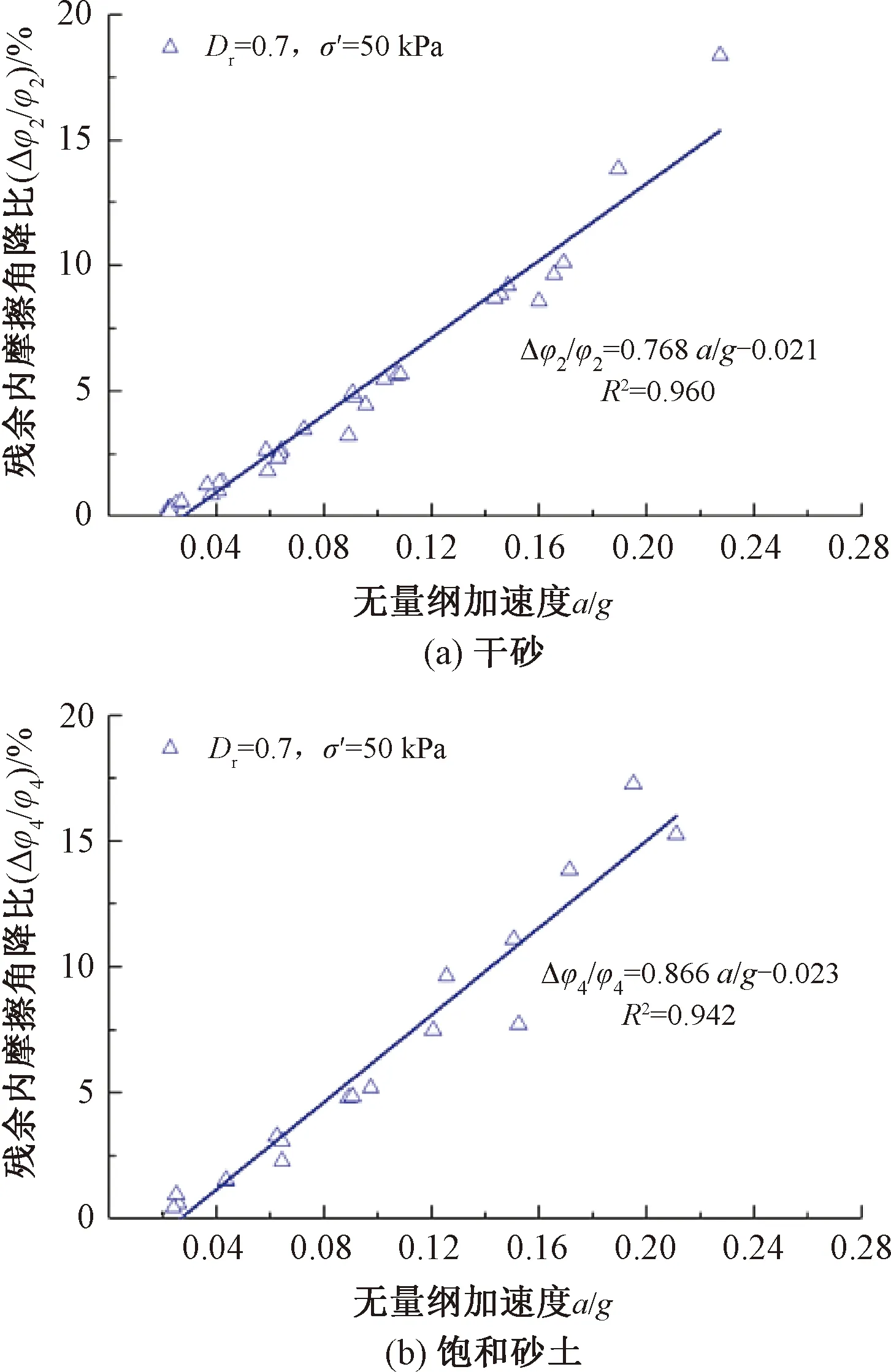
图8 砂土残余应力状态下干砂、饱和砂土内摩擦角降比与加速度的关系

由图8可知,当加速度a≤0.02g时,砂土残余内摩擦角降比很小,几乎可以忽略不计;当加速度a>0.02g时,砂土残余内摩擦角逐渐衰减,砂土残余内摩擦角降比与加速度幅值成正比。这是由于砂土的残余抗剪强度依然能够抵抗较小的附加振动。此时,砂土颗粒排列较为紧密,较小振动能量下砂土颗粒间的摩擦难以被克服,故当加速度较小时,砂土残余内摩擦角衰减较小。而随着振动加速度的不断增大,砂土颗粒间的相互作用被逐渐克服,砂土残余抗剪强度逐渐减小,残余内摩擦角降比逐渐增大。

在60 Hz循环荷载作用下,残余应力状态下加速度幅值与砂土残余内摩擦角降比的关系见图9。由图9可知,当加速度a≤0.02g时,干砂与饱和砂的残余内摩擦角降比均较小,几乎为零,即砂土的含水率对结果影响不大;当a>0.02g时,对于给定的加速度,干砂与饱和砂的残余内摩擦角降比差异也较小。随着振动加速度的增加,砂土的残余内摩擦角降比几乎不受含水率的影响。此外,饱和试样在基于固结排水条件下进行的,即超孔隙水压力不会累积且在较短的时间内很快消散,从而导致超孔隙水压力对饱和砂土残余抗剪强度的影响不显著,干砂和饱和砂的试验结果差异不大。因此,在静载与高频循环荷载耦合作用下,本试验振动加速度范围内饱和砂与干砂的残余抗剪强度变化差异不大。

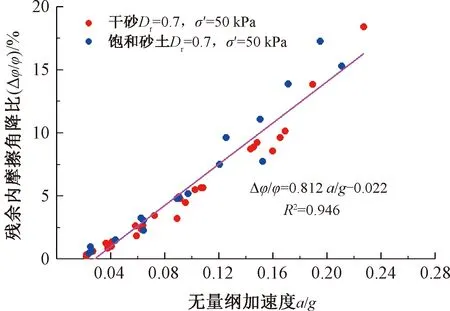
图9 残余应力状态下干砂土与饱和砂土对比

3.2 初始相对密实度对砂土残余内摩擦角的影响

在60 Hz循环荷载作用下,干砂土初始相对密实度对残余内摩擦角降比的影响见图10。图10中,Dr分别为0.4、0.7,有效围压σ′分别为30、50、70 kPa。由图10可知,干砂初始相对密实度对残余内摩擦角降比影响不大。

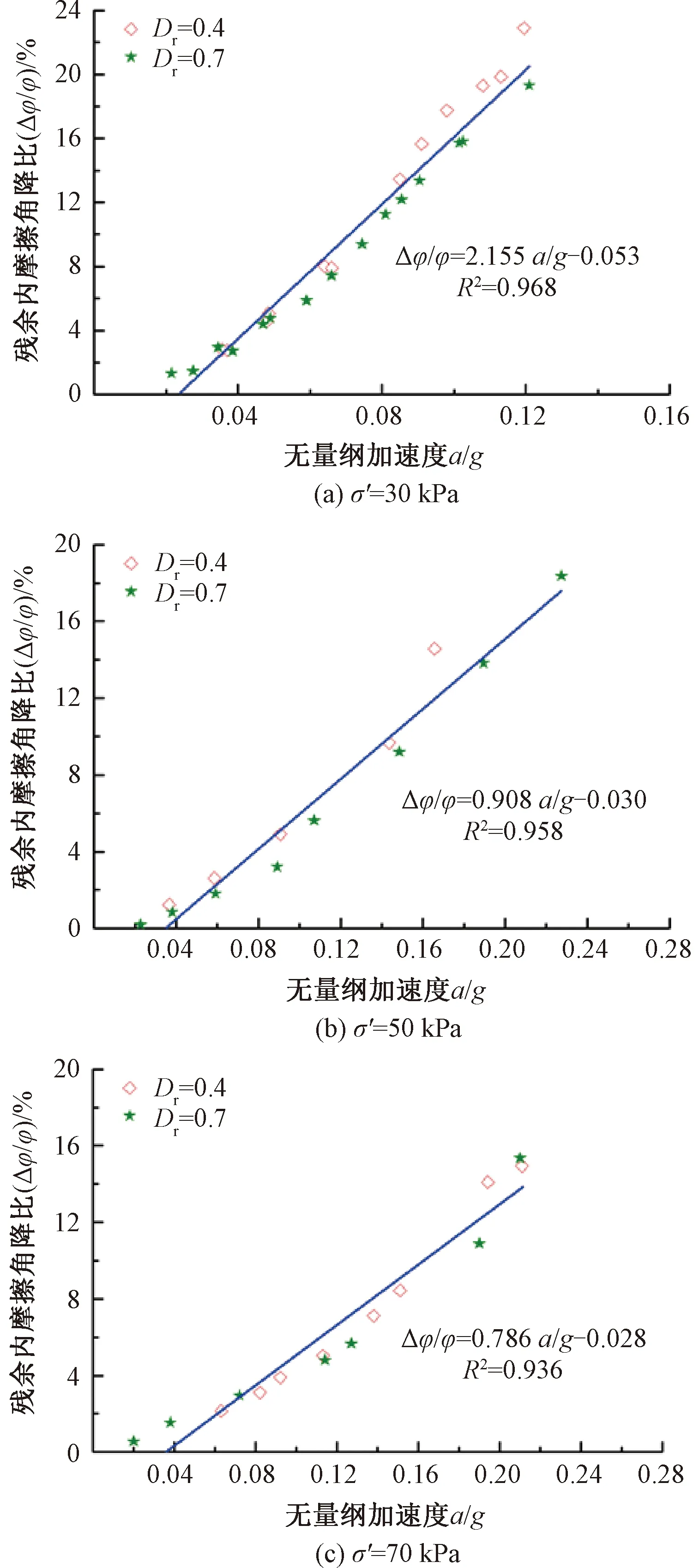
图10 干砂土残余应力状态下不同初始相对密实度的影响

由静三轴试验可知,剪切初始阶段,不同初始相对密实度的干砂试样孔隙比差异较大,Dr=0.7时干砂试样经历强度上升阶段、峰值应力阶段、应变软化阶段,最终到达残余应力状态阶段,即临界状态阶段。Dr=0.4时干砂试样,强度首先以较快的速率上升,随后上升速率开始减慢,最终达到一个稳定的强度。此密实度下的干砂试样强度一直在上升,最终的稳态强度与Dr=0.7的干砂试样差异不大。临界孔隙比与初始相对密实度大小无关,由于干砂在不同初始相对密实度下的最终孔隙比均接近临界孔隙比,故不同初始相对密实度的干砂试样残余抗剪强度较为接近。因此,在给定的振动强度下,干砂残余抗剪强度损失状况差异不大,残余内摩擦角降比差异也不大。

在60 Hz循环荷载作用下,饱和砂土初始相对密实度对残余内摩擦角降比的影响结果见图11。图11中,砂土Dr分别为0.4、0.7,有效围压σ′分别为30、50、70 kPa。由图11可知,Dr对饱和砂土残余内摩擦角降比影响不大,即Dr对饱和砂土残余抗剪强度损失影响不大。

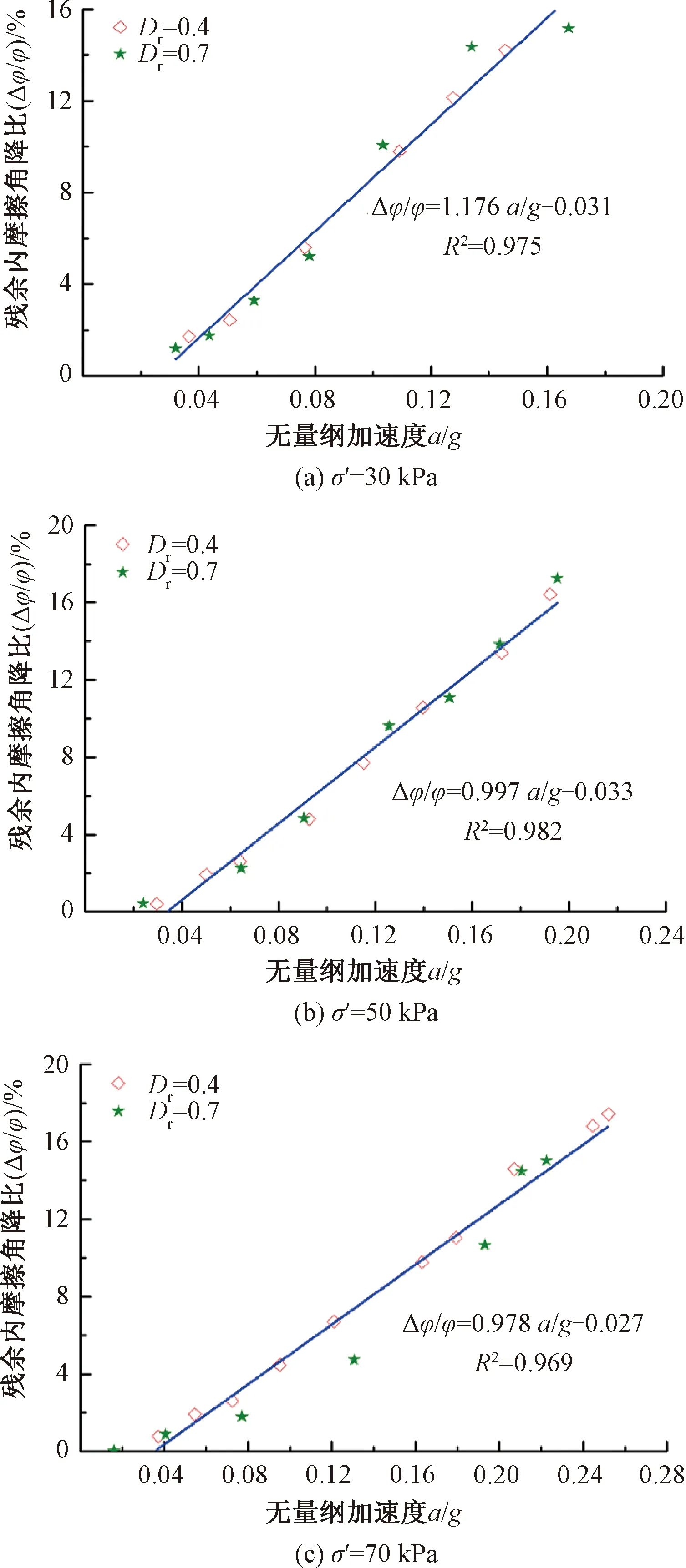
图11 饱和砂土残余应力状态下不同初始相对密实度的影响

从上述试验结果可以看出,初始相对密实度对砂土残余内摩擦角降比的影响不大。针对此规律,干砂土与饱和砂土基本一致。

3.3 有效围压对砂土残余内摩擦角的影响

(1)有效围压对干砂残余内摩擦角降比的影响

有效围压对干砂内摩擦角降比的影响见图12。对Dr分别为0.4、0.7的干砂试样施加60 Hz循环荷载。当振动加速度a>0.02g时,随着振动加速度的增大,干砂残余内摩擦角降比随加速度呈线性增大,此规律与有效围压大小无关,可以认为是无黏性材料自身的特性。

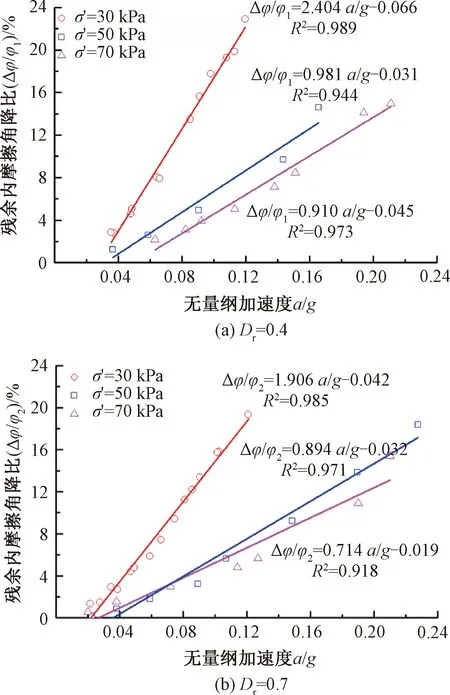
图12 干砂残余应力状态下不同有效围压的影响

有效围压对干砂残余内摩擦角降比的影响见图12(a)。图12(a)中,干砂试样的Dr=0.4,有效围压σ′分别为30、50、70 kPa。由图12(a)可知,当a≤0.02g时,干砂残余内摩擦角降比较小,σ′对干砂残余内摩擦角降比影响不显著;当a>0.02g时,σ′的影响开始显现。对于给定的振动加速度,随着σ′增大,干砂残余内摩擦角降比减小。当σ′从30 kPa增大到70 kPa时,Dr=0.7的干砂残余内摩擦角降比相差最大可达16%。

图12(b)同样反映了Dr对干砂残余内摩擦角降比的影响。图12(b)中,选取Dr=0.7,σ′分别为30、50、70 kPa。由图12(b)可知,当a≤0.02g时,干砂残余内摩擦角降比较小,σ′对于残余内摩擦角降比影响不显著;而当a>0.02g时,σ′的影响开始显现,对于给定的a,随着σ′的增大,干砂残余内摩擦角降比减小。当σ′从30 kPa增大到70 kPa时,Dr=0.7的干砂残余内摩擦角降比相差最大可达13%。

(2)有效围压对饱和砂土残余内摩擦角降比的影响

饱和砂土残余内摩擦角降比同样受到有效围压的影响较大。不同初始相对密实度下有效围压对饱和砂土残余内摩擦角降比的影响见图13。为便于对照,保证试验结果的准确性,对Dr分别为0.4、0.7的饱和砂土试样施加60 Hz循环荷载。在残余应力状态下,当a>0.02g,随着a的增大,饱和砂土残余内摩擦角降比都呈线性增大,此规律与施加的σ′大小无关,同样可以认为这是无黏性材料自身的特性。

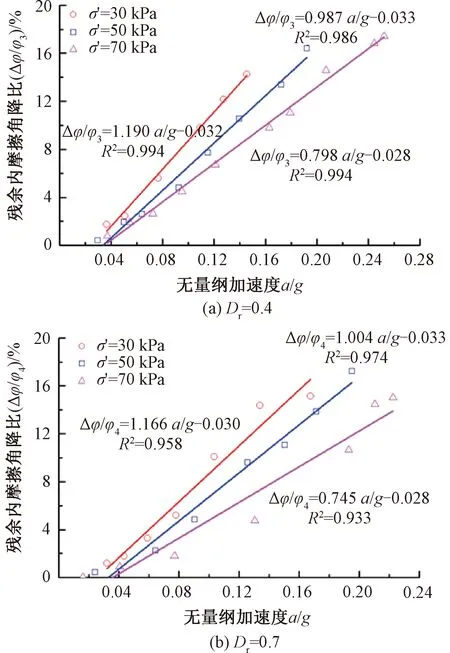
图13 饱和砂土残余应力状态下不同有效围压的影响

由图13(a)可知,对于Dr=0.4的饱和砂土试样,当a≤0.02g时,饱和砂土残余内摩擦角降比较小,几乎可以忽略,此时σ′对饱和砂土残余内摩擦角降比的影响不明显。当a>0.02g时,σ′对饱和砂土残余内摩擦角降比有显著影响。即随a的逐渐增大,σ′越大,饱和砂土残余内摩擦角降比越小。原因与σ′对干砂残余内摩擦角降比的影响相同。当σ′从30 kPa增大到70 kPa时,Dr=0.4的饱和砂土残余内摩擦角降比相差最高可达6%。

由图13(b)可知,σ′的影响规律与Dr=0.4的饱和砂土试样基本一致,原因与相同密实度的饱和砂土相同。当σ′从30 kPa增大到70 kPa时,Dr=0.7的饱和砂土残余内摩擦角降比相差最大可达7%。

综上所述,σ′对干砂和饱和砂土的残余抗剪强度损失有着重要影响,相对于饱和砂土,干砂受σ′的影响更大。

3.4 振动频率对砂土残余内摩擦角降比的影响

本试验选取不同的振动频率(1、5、10、15、20、25、30、35、40、60、80、100 Hz)研究振动频率f对土体残余抗剪强度损失的影响。音圈电机的输出由安培力方程F=B×I×L控制,其产生的激振力与所施加的电流强度成正比。一个恒定的输入功率对应于一个恒定的输入力,因此采用控制输入功率,改变f的方法来研究振动频率对砂土残余内摩擦角降比的影响。本节选取4个不同的输入能量等级(level 1—level 4)来研究不同能量等级下振动频率对砂土残余内摩擦角降比的影响。

f对Dr=0.7、σ′3= 50 kPa的砂土残余内摩擦角降比的影响见图14。level 1—level 4是逐渐增大的输入功率,其动应力逐级增大。对于固定的f,随着输入能量的增大,砂土残余内摩擦角降比相应增大。输入能量较低(level 1、level 2)时,f对砂土残余内摩擦降比影响较小,高低频振动产生的差异不显著,即当音圈电机输入功率较小时,试样受到的振动幅值难以克服土体颗粒间摩擦,f对砂土抗剪强度损失的影响不大。

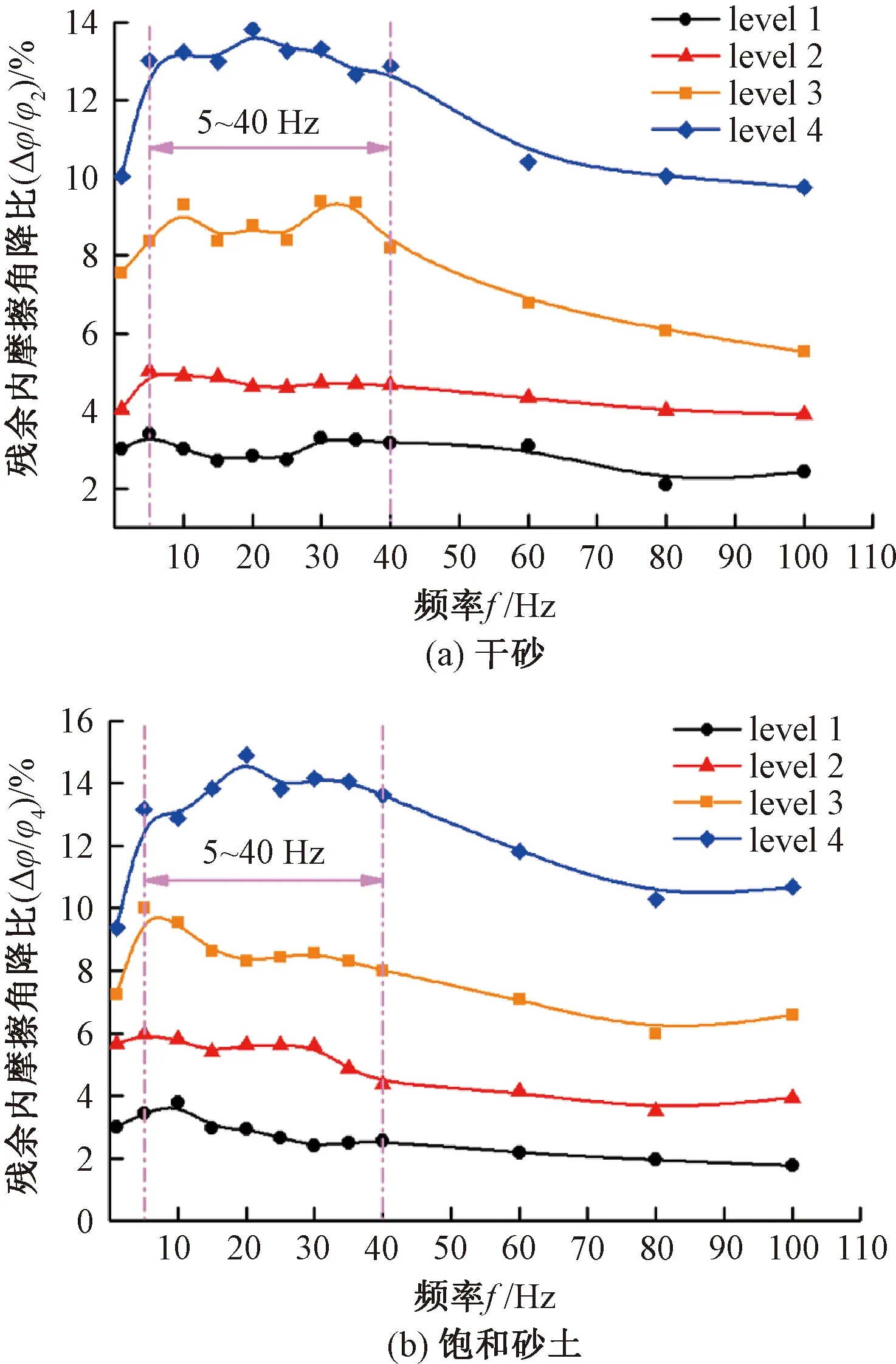
图14 振动频率对干砂、饱和砂土残余内摩擦角降比的影响

当能量较高(level 3、level 4)时,振动频率对砂土残余内摩擦角降比影响较大,高低频振动产生了明显的差异。在f=1 Hz时,其残余内摩擦角降比较小。在5～40 Hz频率范围出现砂土残余内摩擦角降比最大的频段。对于该敏感频域范围砂土摩擦角降比的突增,可能是该频段范围的振动引起试样的共振。当f高于40～60 Hz时,砂土残余内摩擦角降比随f的增大而减小。当f>60 Hz时,砂土残余内摩擦角降比差值较小,但仍然比低频振动引起的内摩擦角降比大。

试验结果表明,高频振动产生的内摩擦角降低大于低频循环荷载产生的影响,同时会产生一个引起砂土内摩擦角降比突增的敏感频段[23]。对比振动频率和加速度幅值两个动力参数,可以发现振动加速度幅值对内摩擦角降比的影响占主导地位。对于敏感频段的确定,将在后续研究中进行共振柱试验,与砂土的共振频率进行对比分析,从而建立残余强度和振动频率的定量关系。

4 结论

本文采用自主研制的可施加高频循环荷载的三轴仪,在砂土接近残余应力状态下进行静载与高频循环荷载耦合的三轴试验,研究砂土在不同初始状态和振动条件下的残余抗剪强度损失规律。通过对不同影响因素下砂土残余抗剪强度损失规律的研究,主要得到如下结论:

(1)残余应力状态下,砂土在高频循环荷载作用下会出现残余抗剪强度损失的现象。当试样接近残余应力状态时,所施加的高频循环荷载会迅速引起试样抗剪强度的损失。当振动停止后,随着单调剪切的进行,试样强度会恢复至之前的水平。即所施加的高频循环荷载对砂土试样振动前后的残余抗剪强度没有长期影响。

(2)振动加速度对砂土的残余抗剪强度损失有较大影响。当振动加速度a≤0.02g时,砂土残余内摩擦角降比与振动加速度关系不明显。在此较小加速度范围内,砂土残余内摩擦角降比很小,几乎可以忽略不计;当加速度a>0.02g时,随着加速度幅值的增大,砂土残余内摩擦角降比随之增大,残余内摩擦角降比与振动加速度幅值成正比。

(3)有效围压对高频循环荷载作用下砂土的残余抗剪强度损失有较大影响,该影响与加速度幅值有关。当加速度a≤0.02g时,有效围压对砂土残余内摩擦角降比影响不大;而当加速度a>0.02g时,在给定的振动加速度条件下,有效围压越大,砂土残余内摩擦角降比越小,有效围压与残余内摩擦角降比成反比。砂土初始相对密实度和含水率对高频循环荷载作用下砂土残余抗剪强度损失的影响较小。

(4)振动频率对砂土残余内摩擦角降比有影响,引起砂土残余内摩擦角降比最大的敏感频段为5～40 Hz。当振动频率高于40 Hz时,砂土残余内摩擦角降比随着振动频率的增大而减小。振动加速度幅值对内摩擦角降比的影响大于振动频率的影响。

为从机理上探究散体材料的高频响应特征,本研究采用了粒径较为统一的福建平潭标准砂,避免了散体材料参数变异性对实验结果的影响。在后续研究中将进一步分析符合实际级配的基床散体填料在高频荷载作用下的强度演化规律,揭示运行速度为400 km/h及以上高铁路基基床可能存在的长期服役安全隐患,为其路基动力设计提供理论依据。