山地模块化电动底盘的同侧输出行星减速器设计*
2023-09-11向浩高巧明韦增健许鹏曾俊豪赵鹏飞
向浩,高巧明,2,3,韦增健,许鹏,曾俊豪,赵鹏飞
(1. 广西科技大学机械与汽车工程学院,广西柳州,545006; 2. 广西汽车零部件与整车技术重点实验室,广西柳州,545006; 3. 广西合浦县惠来宝机械制造有限公司,广西北海,536100)
0 引言
近年来“碳中和”概念持续走红,各国都提出相关的举措,其中研发新能源汽车成为主要措施之一,随着投入的增加,电动汽车的发展取得重大进步,与电动汽车发展相比电动农业底盘发展十分缓慢[1]。现有电动农业底盘在丘陵山地适应性较差,在农用底盘上使用现有化工机械和矿山机械的行星减速器[2],存在着体积大,不易安装等问题,使用机器人的行星减速器,存在着可靠性差、承载差等问题,均不适应农田的复杂工况作业。2017年美国约翰迪尔公布了全电动拖拉机SESAM,充满电可持续工作4 h;同年,美国爱科旗下的Fendt推出了E100系列电动拖拉机,具有50 kW的功率输出。2020年国家农机装备创新中心发布了具有轮边驱动技术的ET1004-W电动拖拉机[3]。
目前,电动底盘的发展,大多数厂商只是在原有底盘的基础上,将动力源发动机拆除,在发动机处安装电动机作为动力源,继续沿用原有的传动系统,不利于智能化升级[4-6]。
本文针对农业动力底盘通过性差,农业机械行星减速器发展缓慢、可靠性差等问题,采用模块化设计理念,针对丘陵山地工况和地形地貌特点,设计独立的三角橡胶履带牵引模块[7-8];再通过优化设计理念,设计一款动力同侧输出且输入轴与输出法兰同轴的二级行星减速器,解决农机行星减速器可靠性差的问题。
1 山地模块化电动底盘结构
山地模块化电动底盘采用模块化设计理念,由功能模块、牵引模块、属具模块、属具快换装置等组成,并且底盘采用纯电驱动模式,可以实现零排放和低噪作业。牵引模块通过和不同的功能模块组合可以实现载人和载物的切换,再通过安装不同的属具模块,可以完成割草、开沟、施肥等工作。山地模块化电动底盘主要参数如表1所示。

表1 山地模块化电动底盘主要设计参数Tab. 1 Main design parameters of the mountain modular electric chassis
山地模块化电动底盘的牵引模块为独立模块,将轴向磁通电机和行星减速器集成在牵引模块中,再通过集成的独立悬架与功能模块连接,实现了牵引模块自有动力功能,通过电缆从功能模块获取能源从而驱动底盘行走,消除了功能模块受动力源布置的设计限制,能实现更多的作业功能;实现了横向地形的自适应功能,两端牵引模块相对于功能模块独立的上下浮动,保障底盘在横向工作时,人员的安全和属具模块的作业效果。
轴向磁通电机和行星减速器在牵引模块中不同的布置方案对整个底盘的性能有着诸多的影响。如图1(a)所示为牵引模块的布置方案一,行星减速器一端安装轴向磁通电机,另一端安装履带总成,此布置方式底盘整机宽度为1 200 mm,履带中心距为950 mm,牵引模块独立悬架长度400 mm。如图1(b)所示为牵引模块的布置方案二;行星减速器安装于履带总成的外侧,电机安装于履带总成的内侧,形成了行星减速器同侧安装轴向磁通电机和履带总成的布置方式,此布置方式底盘整机宽度为1 000 mm,履带中心距为750 mm,牵引模块独立悬架长度250 mm。
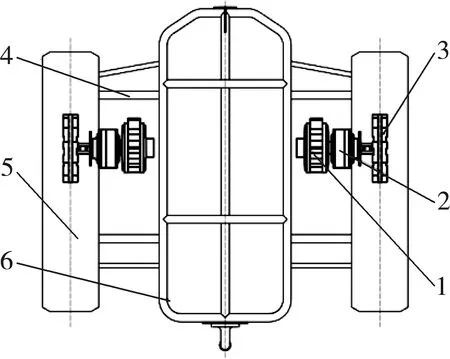
(a) 牵引模块方案一
针对两种布置方案使用运动学仿真软件对牵引模块和独立悬架的运动进行分析,如图2所示为牵引模块履带的横向和纵向的位移变化曲线。方案一,由于电机和履带的安装,导致独立悬架摆臂的长度相比于方案二更长。根据履带横向和纵向的位移变化量数据计算分析,在相同的纵向位移的情况下,方案二,履带的横向位移相比于方案一履带的横向位移平均降低了13.9%,使得履带磨损降低,延长了履带的使用寿命,并且方案二的行星减速器安装于履带总成的外侧,电机安装于履带总成的内侧,使得底盘宽度较窄,通过性更好。

图2 履带位移变化曲线
通过行星减速器同侧安装轴向磁通电机和履带总成的布置方案进行分析,设计了一款动力同侧输入输出的行星减速器。行星减速器的输入轴和输出法兰位于同侧,因此该行星减速器安装于两端履带的外侧。履带的牵引力由直接安装在履带总成上的两个独立轴向磁通电机提供,轴向磁通电机的输出轴与行星减速器的输入轴连接,行星减速器的输出法兰直接连接履带的驱动轮带动履带行走。履带驱动轮采用轮边驱动、轮边减速的方式以及两侧履带独立的电气控制,满足了高效率、低成本、体积小、控制方便、机动灵活的设计要求[9],如图3所示。
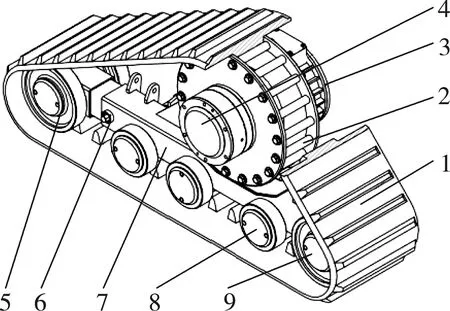
图3 山地模块化电动底盘牵引模块
2 行星减速器结构设计
2.1 行星减速器结构设计
山地模块化电动底盘主要应用于丘陵山地,需要克服丘陵山地的复杂环境作业,因此对牵引模块的牵引力要求较高,从而要求行星减速器在低转速时能够提供高扭矩。根据山地模块化电动底盘牵引模块的电机、减速器、驱动轮的布置方案以及减速要求,设计了动力同侧输出且输入轴与输出法兰同轴的二级行星减速器。行星减速器机构简图如图4所示,通过二级行星轮系减速,使用NGW型行星减速方式,满足电驱动底盘的减速器的传动要求;采用输入轴与输出法兰重叠的方式以实现动力的同侧输入输出;两级行星轮系均采用4个行星轮的分布方式,增加传动的平稳性,从而具有体积小、承载能力大的优势[10]。
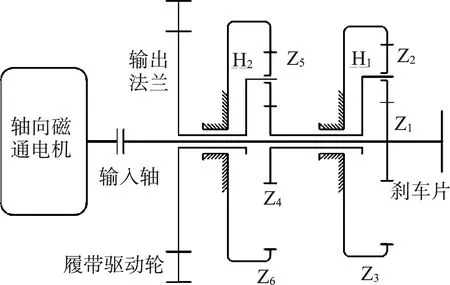
图4 二级行星减速器机构简图
2.2 行星减速器三维建模建立
行星减速器由箱体、箱盖、行星轮系、输入轴、输出法兰等组成,其中行星减速器箱体是整个行星减速器的基本骨架,是支撑行星轮系传递动力的重要承载体,根据箱体的设计要求及其原理进行设计,使其强度、刚度满足要求。根据确定的减速器类型和机构简图的运动关系,按照减速器相关原理的设计准则进行各零部件的设计,并建立行星减速器各零件三维模型,按照运动关系将各零件装配,行星轮系结构三维模型如图5所示。
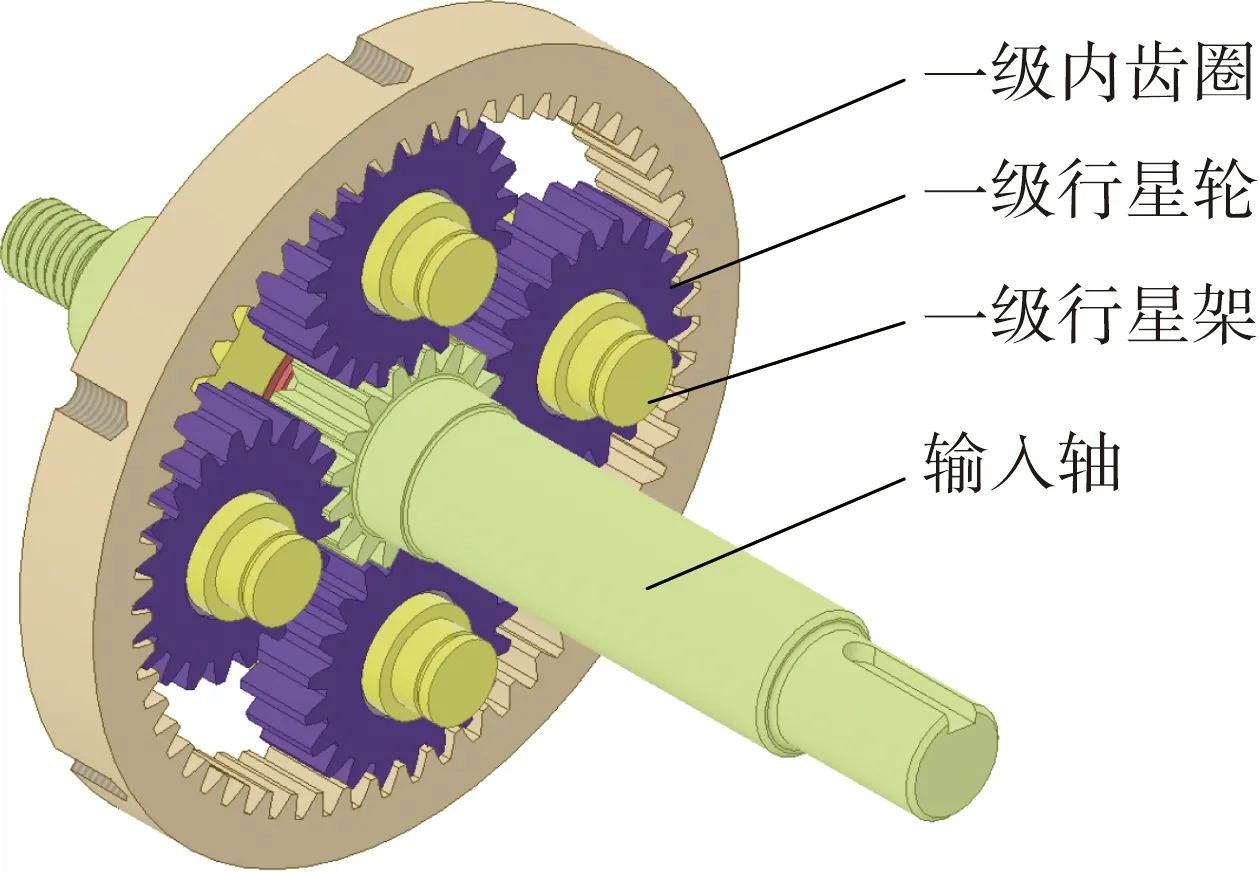
(a) 一级行星轮系结构
3 行星减速器参数计算
3.1 行星减速器传动比计算
山地模块化电动底盘采用两个轴向磁通电机作为动力源,单个轴向磁通电机的额定功率P=4 kW,额定转速n0=3 000 r/min,山地模块化电动底盘速度的设计要求为V=15 km/h,驱动轮的半径rp=200 mm。按照设计要求的最大速度计算减速器的传动比,如式(1)所示。
(1)
根据传动比计算,取二级减速器的传动比为i=15。
3.2 传统设计方法确定齿轮参数
针对行星减速器首先采用传统设计方法,以传动比i=15为设计目标,以满足同心要求和装配条件为设计要求,经过多次的修改得到满足设计齿数参数,如表2所示。传统设计以静态设计为主,设计目标、要求较为单一,不能满足行星减速器的多目标设计需求,与现代设计方法相比具有较大的劣势。
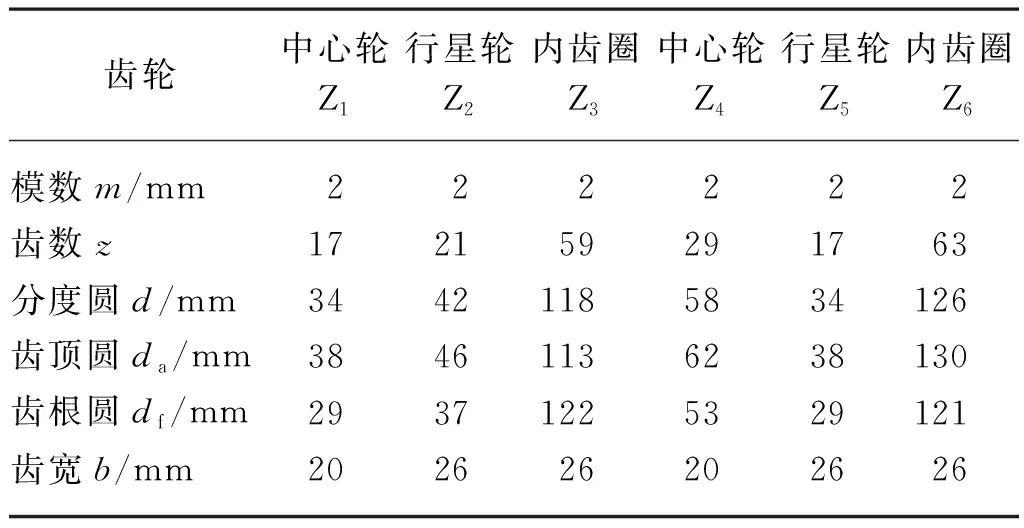
表2 传统齿轮设计主要参数Tab. 2 Main parameters of traditional gear design
3.3 行星减速器齿轮参数优化设计
山地模块化电动底盘牵引模块为独立模块且牵引模块上安装有行星减速器和轴向磁通电机,为满足牵引模块的安装要求和性能要求,行星减速器的体积需要减小,但随着体积的减小,其强度将会下降,为满足体积要求和强度要求,运用可靠性理论及优化设计技术[11],通过设计变量、建立目标函数,再通过约束条件的限制,获得最优的齿轮齿数参数。使用优化设计理念设计行星减速器,可以缩短设计周期,提高产品经济性[12]。
3.3.1 目标函数的建立
受到牵引模块的限制,需要减小各部件的尺寸,从而达到减小行星减速器的尺寸的要求,在尺寸减小的同时需要保证减速器各部件的强度,使其能传递所需的扭矩。以行星减速器的体积作为设计准则,以齿轮体积之和最小为目标[13],优化参数变量如式(2)所示。
X=[x1、x2、x3、x4、x5、x6]T
(2)
式中:x1、x2、x3、x4、x5、x6——齿轮Z1、Z2、Z3、Z4、Z5、Z6齿数。
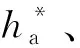

(3)
式中:m——齿轮模数;
b1、b2、b3、b4、b5、b6——各齿轮齿宽。
3.3.2 约束条件
按照可靠性理论与优化设计要求设置约束条件,通过约束条件对目标函数进行限制,可以保证设计的行星减速器尺寸合理,工作稳定可靠。
1) 同心条件。太阳轮与内齿圈需要共轴且行星轮绕着此轴做回转运动,所以需要行星轮的分度圆与太阳轮和内齿圈的分度圆相切,故需满足同心条件式(4)。
Za+2Zb=Zc
(4)
式中:Za——太阳轮齿数;
Zb——行星轮齿数;
Zc——内齿圈齿数。
根据同心条件确定约束函数为
f1(x)=x1+2x2-x3=0
(5)
f2(x)=x4+2x5-x6=0
(6)
2) 装配条件。行星轮系在装配时,为保证Np个行星轮均匀分布在内齿圈轴线为圆心的同一圆周上,且Np个行星轮均能与太阳轮和内齿圈正确啮合,需满足装配条件式(7),并根据装配条件建立约束函数式(8)、式(9)。
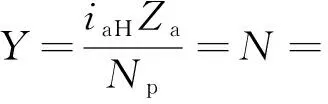
(7)
(8)
(9)
式中:iaH——行星齿轮减速比;
i1H1——第一级行星齿轮减速比;
i4H2——第二级行星齿轮减速比;
n——任意正整数;
Np——行星轮数。
在本设计中,需要行星减速器的体积较小且传递扭矩较大,为保证行星减速器的稳定性和强度,因此选择行星减速器行星轮数Np=4。
3) 邻接条件。行星减速器的减速比大,结构紧凑,为防止邻接行星轮在运动中出现干涉,需要满足邻接条件式(10)。
L>dag
(10)
式中:L——相邻两个行星轮中心距;
dag——最大行星轮齿顶圆直径。
根据邻接条件建立约束函数式(11)、式(12)。
(11)
(12)
4) 不发生根切条件。齿轮使用范成法加工,当齿数较小时,齿轮插刀会将齿轮根部过多切除从而产生根切现象,导致轮齿的抗弯强度下降,影响减速器工作的稳定性,因此在齿轮参数设计时需要避免根切现象的产生,故需满足不发生根切条件式(13),并根据不发生根切条件建立约束函数式(14)。
(13)
(14)
式中:α——齿轮压力角。
在本文中,齿轮为渐开线圆柱齿轮,齿轮的压力角α=20°。
5) 模数与齿宽的约束条件。在行星齿轮设计中,为提高传动稳定性,需满足齿宽条件式(15)、式(16)。
5m≤bn≤17m
(15)
(16)
式中:bn——齿轮宽度;
dmin——最小齿轮分度圆。
相互啮合的小齿轮与大齿轮承受的相同力矩,因此小齿轮齿面承受压力更大,并且小齿轮齿面的啮合次数较多,所以小齿轮的齿宽需要更宽,通常小齿轮的齿宽比大齿轮宽5~10 mm。本设计中选定太阳轮齿宽为20 mm,行星轮与内齿圈齿宽为26 mm。
6) 传动比条件。根据行星减速器传动比计算所得的传动比为15,为简化计算,将行星减速器传动比转化为i=15±1,其传动比条件为式(17),并建立约束函数式(18)、式(19)。
(17)
(18)
(19)
7) 齿轮强度条件。在行星减速器中,太阳轮同时与4个行星轮啮合,啮合次数最多且太阳轮体积较小受到的应力较为集中,工作条件最为恶劣,受力最复杂,因此太阳轮最容易出现失效,所以分析两级行星轮系太阳轮的齿根弯曲强度和齿面接触疲劳强度即可。齿根弯曲强度可靠性根据式(20)计算。
(20)
式中:KF——弯曲疲劳强度载荷系数;
Ta——主动轮转矩;
YFa——齿型系数;
YSa——应力修正系数;
Yε——重合度系数;
φd—齿轮宽径比;
σF——弯曲疲劳强度;
[σF]——弯曲疲劳许用应力。
齿根弯曲强度可靠性计算式,确定其弯曲强度约束函数式(21)、式(22)。
f10(x)=2KFTaYFaYSaYε-[σF]φd1m3x12≤0
(21)
f11(x)=2KFTaYFaYSaYε-[σF]φd2m3x42≤0
(22)
根据机械设计手册[15]以及直齿轮和斜齿轮承载能力计算标准[16]可得:KF=1.65、YFa=2.97、YSa=1.52、Yε=1.02、[σF]=505 MPa、KF=1.65、T1=95 N·m、T2=425 N·m。齿面接触疲劳强度可靠性计算如式(23)所示,所建立的约束函数为式(24)、式(25)。
(23)
(24)
(25)
式中:KH——接触疲劳强度载荷系数;
ZH——区域系数;
ZE——弹性影响系数;
Zε——重合度系数;
σH——接触疲劳强度;
[σH]——接触疲劳许用应力;
u——齿数比。
根据机械设计手册[15]以及直齿轮和斜齿轮承载能力计算标准[17]可得:KH=1.3、ZH=2.5、ZE=189.8 MPa1/2、Zε=0.876、σH=640 MPa。
3.3.3 数学模型的建立
根据优化设计方法和机械设计理论,建立动力同侧输出的二级行星减速器齿轮计算数学模型。
(26)
本次优化有1个目标函数,6个设计变量为六种齿轮的齿数,13个约束方程。
3.3.4 目标函数计算
已知P=4 kW,n输入=3 000 r/min,i=15,NP=4,太阳轮材料为40Cr,行星轮和内齿圈材料为20CrMnTi,根据最小体积目标函数以及约束条件进行计算,最终确定了减速器的相关参数。优化后行星齿轮减速器主要参数如表3所示。
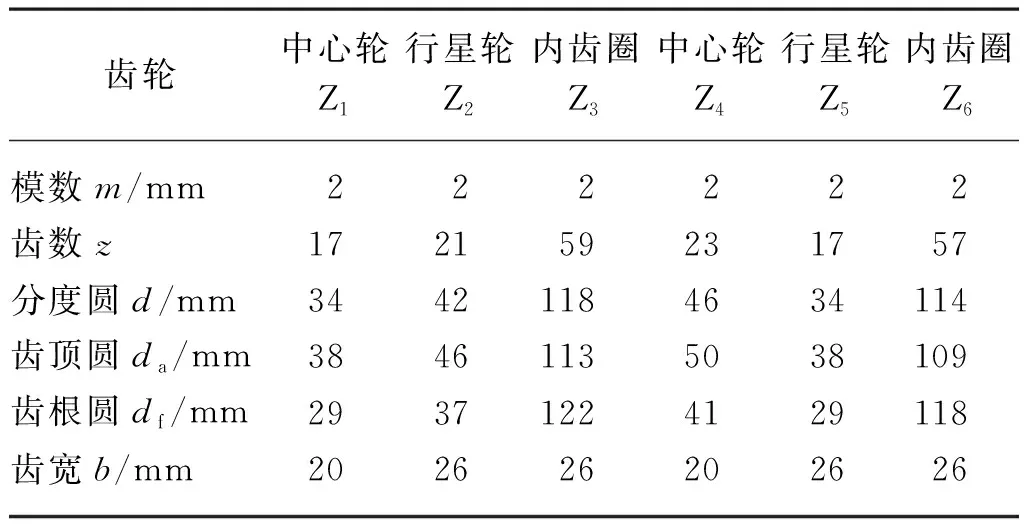
表3 行星齿轮减速器优化后各齿轮参数Tab. 3 Planetary gear reducer after optimization of the gear parameters
3.4 优化结果分析
通过对比传统设计和优化设计所得参数可以得到,优化后的行星减速器中心轮Z1齿数为17,行星轮Z2齿数为21,内齿圈Z3齿数为59,中心轮Z4齿数为23,行星轮Z5齿数为17,内齿圈Z6齿数为57,其中中心轮Z4齿数以及内齿圈Z6齿数降低,优化前行星轮系总体积为219 128 mm2,优化后行星轮系总体积为207 599 mm2,总体积相比之前降低5.3%。最大齿轮的原直径为130 mm,优化后直径为122 mm,径向尺寸相比之前降低6.2%。
4 传动装置分析
4.1 传动装置模态分析
行星齿轮减速器能够传递大扭矩、高转速的动力,这样的动力将引起振动。振动将导致减速器的疲劳损坏,更有可能引发共振,导致整个行星减速器快速损坏,所以对其进行模态分析十分必要[18]。对传动装置采用自适应的划分方法,回转体划分为六面体网格,其他零件划分为四面体网格。网格划分后单元数量为20 573,单元节点数量为70 421,传动装置有限元模型如图6所示。并对传动装置的材料进行参数设置,零件材料参数如表4所示。
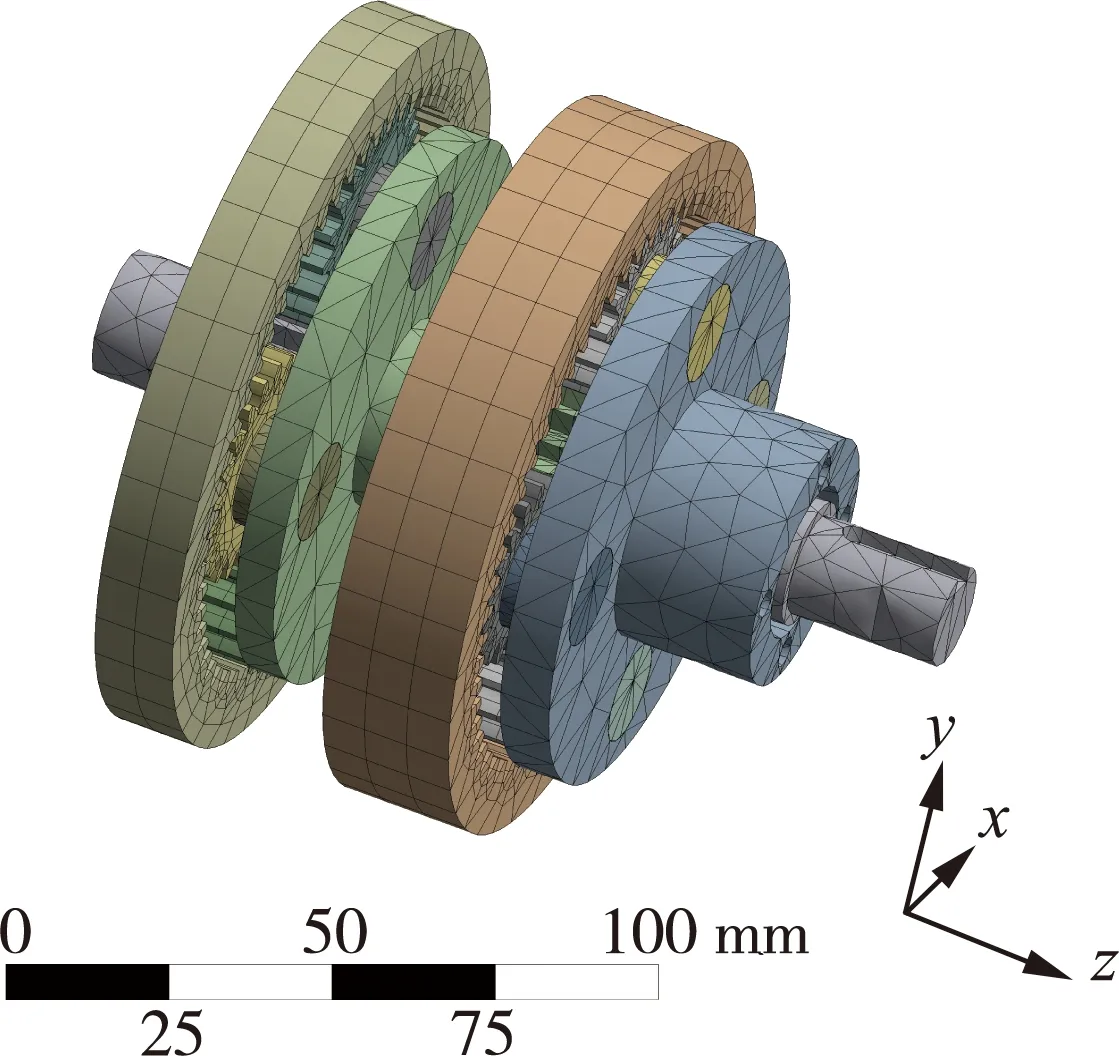
图6 传动装置有限元模型

表4 主要零件材料参数Tab. 4 Main component material parameters
本文所研究的减速器工作频率较低,因此对其模态分析时,无需关注过多阶次的固有频率。故分析传动装置的前5阶固有频率与振型,其振型图如图7所示。

(a) 第1阶
由图7可知,1阶、2阶振动频率为676.94 Hz、680.44 Hz,传动装置输出轴分别绕X轴和Y轴摆动;3阶振动频率为901.71 Hz,行星架Z轴周向摆动;4、5阶振动频率为1 001.1 Hz、1 007.5 Hz,输入轴发生明显的弯曲变形,分别在X轴和Y轴发生弯曲变形。传动装置1阶固有频率为676.94 Hz远大于减速器的振动频率73.91 Hz,故减速器在工作过程中产生的振动不会引起传动装置的共振。
4.2 输出法兰静力学分析
行星齿轮减速器主要作用是降低转速和增大转矩,所以输出法兰将承受非常大的扭矩[19-20]。对行星减速器中受力最大的输出法兰进行静力学分析,可以保证行星减速器结构的强度能够达到要求且行星减速器安全可靠。为提高有限元分析的准确度,且结合输出法兰的形状,采用六面体网格对输出法兰进行网格划分,网格划分后单元数量为12 459,单元节点数量为47 827,输出法兰有限元分析模型如图8所示。
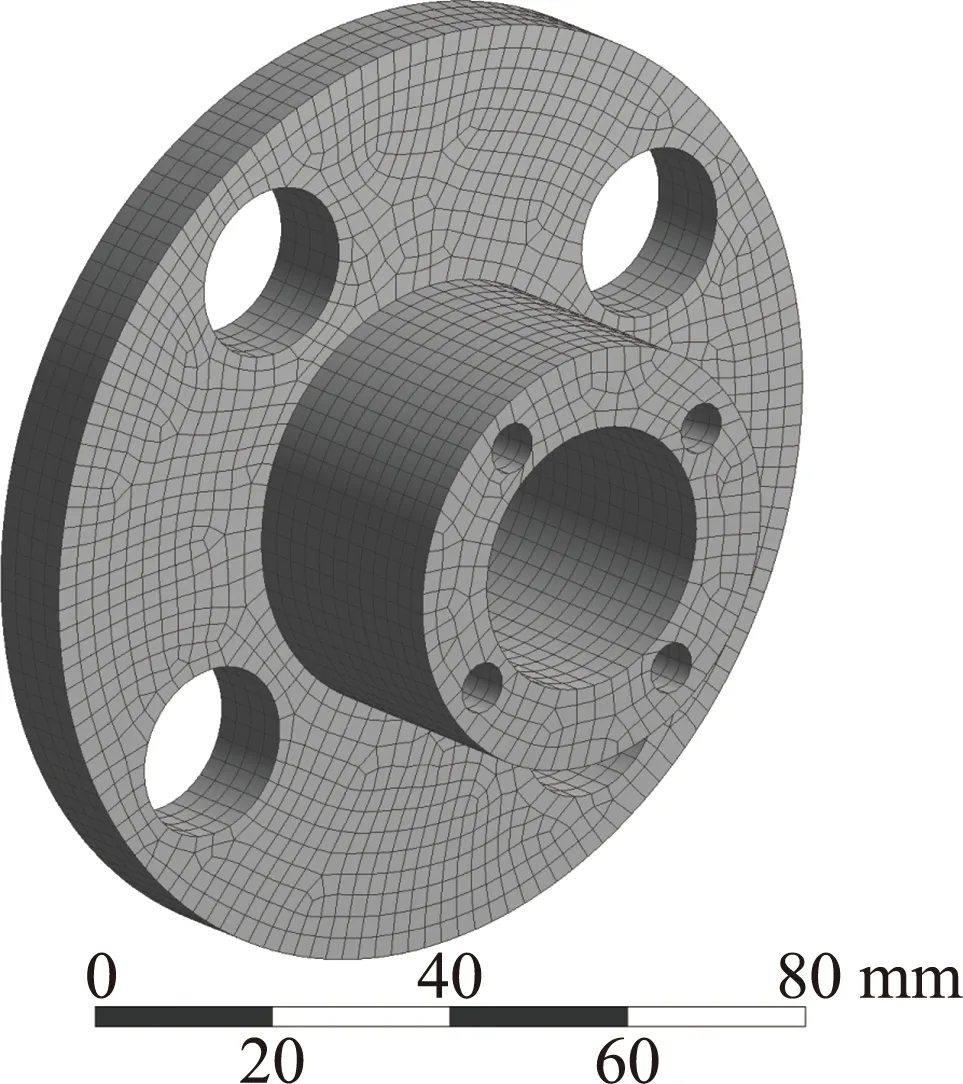
图8 输出法兰有限元分析模型
山地模块化电动底盘设计的工作速度为2 km/h,根据电机功率和减速器传动比以及履带驱动轮直径进行换算,得到电机最大输入转矩为95 Nm,行星减速器的减速比为15,在法兰盘外圆表面上施加1 425 Nm扭矩,再在安装孔处施加固定约束。
通过Ansys分析求解,如图9所示为输出法兰位移云图,最大位移为0.077 794 mm,主要分布在行星架接触孔处及附近,最大变形量较小,能够满足设计的要求。如图10所示为输出法兰应力云图,输出法兰安装孔处和行星架与输出法兰的连接部位处存在应力集中,应力最大值为240.72 MPa,小于40Cr的屈服极限785 MPa,因此输出轴的强度合格,安全可靠。

图9 输出法兰位移云图

图10 输出法兰应力云图
5 结论
1) 本文设计的同侧输出行星减速器能够实现动力同侧输出且输入轴与输出法兰同轴,能满足山地模块化电动底盘的布置方案,从而使得电动底盘的宽度得到减少,通过性能更佳,并且通过运动学仿真可知牵引模块的横向位移平均减少13.9%,使得履带的寿命得到延长,并且同侧输出行星减速器能够低转速高扭矩的输出,提高山地模块化电动底盘的通过性和稳定性。
2) 相比于传统的行星齿轮设计方法,采用可靠性设计理论,以轻量化为设计目标,搭建优化分析模型,最终使得设计的行星减速器行星轮系总体积降低5.3%,径向尺寸降低6.2%,降低总体积和径向尺寸可以节省材料使得安装空间更小。
3) 使用Ansys软件针对传动装置进行模态分析,得到传动装置1阶固有频率为676.94 Hz远大于减速器的振动频率73.91 Hz,故减速器在工作过程中产生的振动不会引起传动装置的共振,对行星减速器关键零件输出法兰静力学分析得到应力最大值为240.72 MPa,小于其材料的屈服极限785 MPa,零件的强度满足要求。
