基于结构方程模型的新工科学生培养多维空间构建实证研究*

2023-09-11李雪莲袁盼盼白花蒲郭俊先张绢朱兴林

中国农机化学报 2023年8期

李雪莲，袁盼盼，白花蒲，郭俊先，张绢，朱兴林

(1. 新疆农业大学机电工程学院,乌鲁木齐市,830052;2. 新疆农业大学交通与物流工程学院,乌鲁木齐市,830052)

0 引言

我国拥有全世界规模最大的工程教育,但由于工程人才培养目标滞后于产业发展、课程内容更新不及时、高等教育历史发展局限等因素,工程教育人才培养的质量还不尽如人意,培养的工科人才与社会行业和产业发展的适应性仍有待提高。为培养更加符合当前社会发展的工程人才,高等工程教育改革创新迫在眉睫[1-2]。

国家大力实施创新驱动发展,提出新工科教学理念,新工科建设坚持问题导向,以学生为中心,培养学生的实践能力和创新能力。为满足新工科发展需求,在新理念、新行动引领下需探索新工科专业人才培养改革,以适应新时代提出的新要求[3-4]。

本文基于新工科教育体系下学生培养多维空间构建的实际现状及问题,采用实证研究法,以新疆农业大学机电工程学院在校生为例开展问卷调查,选取校企合作、教师实践能力、课改情况、实践条件、能力培养机制等5个潜在变量构建学生培养多维空间,采用探索性因子分析法检验所选测量变量对相关问题的解释能力,基于结构方程模型(Structural Equation Model—SEM)构建学生培养多维空间结构方程模型;探索学生对大学教育的收获感和人才培养质量的满意度,在模型适配度良好的基础上,分析了模型运算结果并提出相应优化措施。

结构方程模型(SEM)广泛用于各领域满意度影响因素分析,如:地铁服务质量与乘客满意度构建结构方程模型[5];混合式学习满意度[6];科技创新人才培养的关键路径——来自结构方程模型的经验证据[7];本研究以新疆农业大学机电工程学院在校生为例,根据实际调查数据,构建了基于结构方程模型(SEM)的学生培养多维空间结构方程模型,结合学生学习需求,定量分析各影响因素对学生学习满意度的影响关系。

1 研究路线与方法

1.1 研究路线

本次调查研究使用数据全部源自调研与访谈,采用问卷方式调查学生对大学教育的收获感和人才培养质量的满意度。在剔除无效问卷后,运用SPSS 25.0软件对调查问卷的信度和效度进行检验[8],在调查问卷的信度和效度都符合标准的基础上,结合结构方程模型相关知识,构建新工科学生培养多维空间结构方程模型,使用AMOS 24.0软件绘制模型结构图并对路径系数进行计算,采用探索性因子分析法检验所选测量变量对相应潜在变量的解释能力[9]。对模型进行适配度检验,若模型适配度符合标准,则结合模型路径系数及因子负荷量对影响因素进行分析,在模型适配度良好的基础上,分析了模型运算结果并提出相应优化措施。

1.2 调查过程

本问卷以新疆农业大学2021届农业机械化及其自动化、机械设计制造及其自动化、电气工程及其自动化、新能源科学与工程专业本科毕业生、在校生为调查对象,问卷设计以学生为中心,问卷对校企协同育人课程体系、双师型教师培养体系、实践教学条件现状、混合式课程改革执行情况和学生能力培养机制五个学生培养“多维空间”开展调查,通过学生视角对现行的“多维空间”构建及运行情况进行综合评价,为揭示新工科教育体系下“多维空间”与学生学习质量提升的内在关联提供数据支撑和理论依据。问卷按照各个层次聚焦点不同而设计针对性问题,题目设计从学生视角出发,本着科学合理、结果可靠原则,在题型选择上尽量选择量表型题目;问卷内容包含三部分:样本对象基本信息、各类实践课程、实验设施、培养机制等的满意度评价问题和对教师教学能力、课改成效等的评价问题,并采用李克特5分量表评价各测量指标,以问卷星方式开展问卷调查,问卷有效填写人次数为1 384,有效率为98%。问卷样本所学专业及所在班级类型的频数分布信息见表1。

表1 样本对象基本信息Tab. 1 Basic information of sample object

由样本基本信息可知,参与本次问卷调查的学生以机械设计制造及其自动化专业、汉语班的居多,占比超过50%;其次参与调查的农业机械化及其自动化专业学生占比达到20%。

以上两个占比较大的专业为机电工程学院新工科体系下重点建设专业,同时以汉语班学生为主(包括19级、20级大类招生学生),故样本符合问卷调查需求,数据来源真实有效。

1.3 问卷信效度检验

信度(Reliability)是测量研究数据或研究结果是否具有一致性或稳定性的有效指标。证明其是否有效通过测量表达问题[10]。本文使用目前较常用的克隆巴赫α信度系数法(Cronbach’s Alpha)测量问卷的信度系数。

(1)

式中:k——题目总数;

S——同类问题总分的方差;

Si——题目i所得分数的方差。

对数据进行信度检验,Cronbach’s Alpha值为0.902,大于0.7,认为问卷总体数据可信。各潜变量分别做信度检验,使得每个潜变量的题项数据达到最大可信水平。通过对问卷测量变量的信度分析,由表2可知,本文设定的5个潜变量因子的Cronbach’s Alpha系数中有3个均高于0.9,1个高于0.7,只有1个高于0.6,表明各个测量变量有较高的一致性和相关性,证明测量数据符合结构方程模型的要求,可靠程度较高。

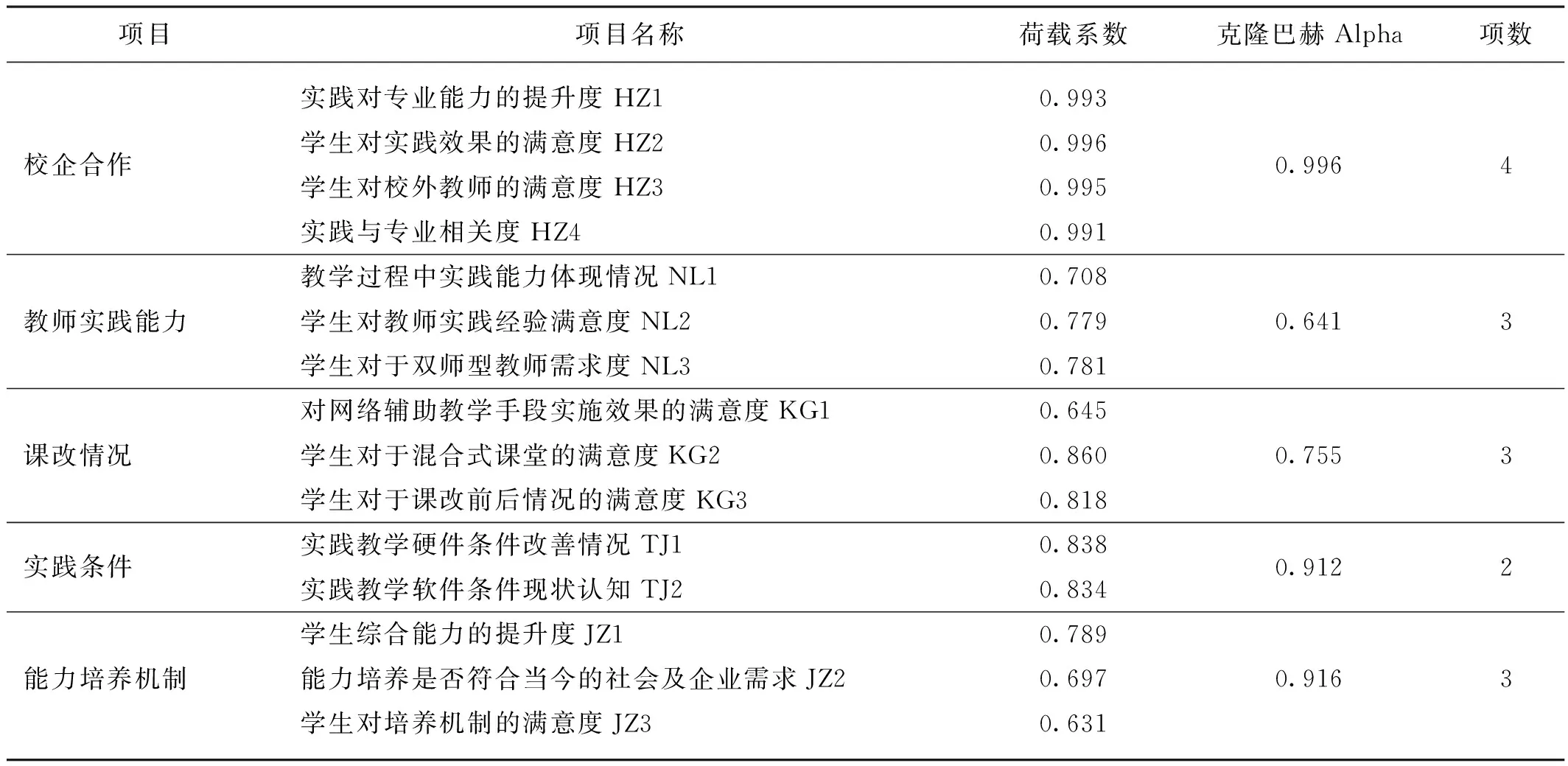
表2 信度分析结果Tab. 2 Results of reliability analysis

本文对量表效度的检验使用结构效度方法。

(2)

式中:rij——变量xi和xj的相关系数;

pij——变量xi和xj在控制其他变量不变条件下的偏相关系数;

KMO——用于检验是否适合因子分析的指标。

KMO值大于或等于0.6时,可进行因子分析[11],其越趋近于1,相关性越高,越适合进行因子分析。使用SPSS 25.0软件对本次调查数据进行效度检验,结果见表3。由表3的数据可知,调查问卷的样本数据KMO度量值达到0.925,同时Bartlett球型检验的概率值p也达到显著性标准(p=0.000<0.001),说明本研究得到的问卷调查数据适合作因子分析。

表3 效度分析结果Tab. 3 Results of validity analysis

2 学生培养多维空间结构方程模型构建及分析

2.1 结构方程模型

结构方程模型(Structural Equation Model,SEM)也称协方差分析模型,包含数理统计分析中的线性回归分析和因素分析方法,是对路径分析、探索性因子分析和方差分析等方法的综合运用和改进,结构方程模型主要包括测量模型和结构模型两部分[12]。

1) 测量模型:描述显变量与潜变量之间的关系,相当于探索性因子分析。

测量方程

Y=ΛYη+ε

(3)

X=ΛXξ+δ

(4)

式中:Y——内生指标组成的向量;

X——外生指标组成的向量;

ΛY——Y在η上的因子负荷量;

ΛX——X在ξ上的因子负荷量;

η——内生潜变量向量;

ξ——外生潜变量向量;

ε、δ——内生、外生显变量的误差项。

2) 结构模型:指的是潜变量之间的关系,相当于路径关系分析。

结构方程

η=Bη+Γξ+ζ

(5)

式中:B——因素路径系数矩阵,内生潜变量之间的影响关系;

Γ——因素路径系数矩阵,外生潜变量对内生潜变量的影响关系;

ζ——结构方程残差向量。

2.2 模型假设

学生培养多维空间结构方程模型选取校企合作、教师实践能力、课改情况、实践条件、能力培养机制等5个潜在变量构建学生培养多维空间,采用探索性因子分析法检验所选测量变量对相关问题的解释能力,基于结构方程模型(SEM)构建学生培养多维空间结构方程模型;如表2所示,结构方程模型包含5个潜变量和15个观测变量。

根据已设潜在变量和测量变量,做如下假设。

H1:校企合作对实践条件直接正相关。

H2:校企合作对教师实践能力直接正相关。

H3:校企合作对课改情况直接正相关。

H4:校企合作对能力培养机制直接正相关。

T1:实践条件对课改情况直接正相关。

T2:实践条件对教师实践能力直接正相关。

T3:实践条件对能力培养机制直接正相关。

N1:教师实践能力对课改情况直接正相关。

N2:教师实践能力对能力培养机制直接正相关。

K1:课改情况对能力培养机制直接正相关。

2.3 因子分析

本文采用探索性因子分析法对各影响因素进行分析,从而分析变量设计的合理性。由表4、表5可见所有测量变量的荷载系数均大于0.5,即可以有效地反应各测量变量对潜在变量的影响,且每个指标的分组与前文所设一致,无需对测量模型进行修正。

表4 总方差解释Tab. 4 Total variance of interpretation

表5 旋转成分矩阵Tab. 5 Matrix of rotating component

2.4 学生培养多维空间结构方程模型构建

学生培养多维空间结构方程模型初步假设模型运用AMOS24.0软件建立,代入数据运算结果如图1所示,其中大的椭圆为潜变量,矩形框为观察变量;小的椭圆为误差项;带箭头直线为关联关系或路径依赖;直线上方的数字为经过估计所得的载荷系数或路径系数。

图1 结构模型

2.5 模型适配度检验

由表6可知模型的拟合指数χ2/df为1.6,一般认为该值小于2则模型拟合很好,该值小于3达到标准,近似误差平方根(RMSEA)为0.063,小于0.08。近似误差平方根与模型拟合指数为判断模型是否适配的重要指标,其数值都符合标准,表明本模型拟合良好。拟合优度指数(GFI)、修正拟合优度指数(AGFI)、规范拟合指数(NFI)、增量拟合指数(IFI)等值均大于0.9,这些结果表明,模型适配度达到要求。

表6 模型适配度Tab. 6 Model fit

2.6 模型结果分析

影响学生学习效果及满意度的因素众多,本文在参考相关研究[13-15],设置满意度评价指标的基础上,结合学生培养多维空间构建的实际现状及问题,设计测量变量指标如表2所示。模型估计结果见表7,各个路径关系均显著,即全部假设成立。

表7 模型估计结果Tab. 7 Model estimation results

结合图1标准化系数和表7模型估计结果对潜在变量之间的相互作用机制有如下分析。

1) 校企合作对实践条件、课改情况、教师实践能力以及能力培养机制有正相关作用,其标准化路径系数分别为0.903、0.421、0.591、0.764。其中校企合作对于实践条件的正相关作用路径系数值最大,其正向促进作用最强。在校企合作中的测量变量中实践对专业能力的提升度HZ1的因子负荷量为0.95,对实践与专业相关度HZ4的因子负荷量为0.93,实践对专业能力的提升度和实践与专业相关度对校企合作的影响较强,针对校企合作采取改进措施应从专业能力提升度和专业相关度入手,提高学生实践能力和实践与专业的相关度。

2) 实践条件对课改条件、教师实践能力和能力培养机制具有正相关作用,其标准化路径系数分别为0.571、0.652、0.710。在实践条件的测量变量中实践教学硬件条件改善情况TJ1的因子负荷量为0.94,其对实践条件的影响较强,这一点也符合一旦实施改善教学硬件条件,效果立竿见影这一事实;而实践教学软件条件现状认知TJ2的因子负荷量为0.69,其对潜在变量的解释能力没有教学硬件条件改善情况强,这说明教学软件能力改善情况需要一定的缓冲时间。

3) 教师实践能力对课改情况和能力培养机制有直接正相关作用,其标准化路径系数分别为0.433、0.732。在教师实践能力中的测量变量教学过程中实践能力体现情况NL1的因子负荷量为0.96,说明其对教师实践能力的解释能力最强,最能体现教师的实践能力。

4) 课改情况对能力培养机制直接正相关作用,其标准化路径系数为0.619。在课改情况中的测量变量学生能力培养是否符合当今的社会及企业需求JZ2和学生对培养机制的满意度JZ3的因子负荷量分别为0.88和0.91,对课改情况的影响较大。针对课改情况应从能力培养方向入手,紧跟社会和企业对人才的需求方向。

由于实际调查中的条件限制,本文中样本量仅可满足小样本分析的要求,缺乏结合更多因素对人才培养质量进行宏观分析。后续的相关研究可以结合不同学科专业的不同特征,对潜在变量和测量变量进行调整,并增加样本数量,结合地域条件等因素进行分析。此外,结构方程模型本身具有灵活性,实际应用时可以根据不同研究目的设置不同的路径关系,结合模型分析结果有针对性地进行优化。

3 讨论

综合样本问卷情况,校企合作情况对实践条件的影响程度较大,而对课改情况的影响稍小。出现此结果的可能原因为,学生认为校企合作形式改变了现存实践环节的软、硬件条件,但此类实践合作课程形式较为单一,提出了希望增加课程类型的建议。而校企合作课程目前基于现有课程体系涉及课改方面较少,项目侧重点更偏向于如何利用企业生产实践环境提升学生实践能力。因此校企合作应采取的改进措施:一方面应充分利用企业实践硬件条件,增加生产实践类型,提高学生实践能力和实践与专业的相关度;另一方面应积极利用企业实践软件条件,重构企业实践课程体系,培养学生合作、沟通等多方面综合素质。

课改情况、教师实践能力和能力培养机制受实践条件影响的程度不存在大幅度差异,影响最大的为能力培养机制,影响最小的为课改情况。该结果出现的可能原因:课程改革为不同类型,有基于课程内容设置的改革,有基于课程授课方式的改革。实践条件的改善一定程度上能够促进课程改革的实施,但课程改革并不受制于实践环节的软、硬件条件。能力培养机制中因包含实践能力培养,其与实践条件关联度较高。因此实践条件的改善是完善人才能力培养机制的重要一环,同时对学科建设、师资培养、课程建设等多方面均具备积极促进作用。

教师实践能力是影响课改成败的关键因素,能力培养机制的构建决定了课改的方向,针对课改情况应从能力培养方向入手,紧跟社会和企业对人才的需求方向。

基于上述讨论分析,提出如下建议。

1) 继续深化校企协同育人,重点是加大实践育人的投入力度和重视程度。实践对专业能力的提升度和实践与专业相关度对校企合作的影响较强,因此应该在人才培养的课程体系中加大实践育人环节比例,不断改进校企合作模式,增加学生在企业的锻炼时间以增强实践能力,同时也可以为企业带来一定的经济效益;通过校企协同育人途径在教学过程中探索企业冠名班、联合指导毕业设计、学生校外实践与青年教师实践能力锻炼同步实施等实践育人新方法、新手段,不断提升实践育人质量,使高校教学活动向培养人才的实践创新能力倾斜。

2) 切实重视实践条件对人才培养的关键作用。高校应该用足用好各类实践条件建设项目经费,如,中央财政支持地方发展专项,加大实践教学条件、新设备开发利用建设力度,利用好新设备,开发新实验项目,更新实验、实践教学内容,加强实验室、工程训练中心、实习基地等建设,增加实践场所的硬件投入。同时,结合专业,持续开展学生暑期社会实践活动,不断探讨社会性实践基地的建设[16]。政府通过专项资金支持、税收优惠等手段积极鼓励和引导社会资本建立人才培养基地,为加强人才实践能力培养发挥重要作用。

3) 教师实践能力水平,特别是青年教师的实践能力水平提升对保障学生培养质量具有非常重要的作用;高校特别是地方高校应积极探索“引培结合、资源重组、学研互通”举措,依托省、自治区人才计划和国家对口援疆机制[17],引进高学历、高职称人才,通过从科研院所和企业外聘教师、青年教师到企业与博士后流动站“实训”、教师考证和评行业职称等手段,不断优化师资职称、能力结构,构建高水平的“双师型”教师队伍,建设高水平师资,提升师资等教学资源的效能;同时,基于人才培养的目标规格、教学内容、教学方法三要素开展专业综合改革,通过与“智慧树在线教育平台”等网络平台合作推进混合式教学改革和课程思政进教案、进教学设计、进教学大纲等教学改革建设工作,构筑专业课程群,提升课程高阶性,突出课程创新性,增加课程挑战度,激发学生的学习内驱力,提升学生创新能力。