基于MI-RRT*算法的路径规划研究*

于强，彭昭鸿，黎旦，李利彬，高艺成

☞仿真技术☜

基于MI-RRT*算法的路径规划研究*

于强1，2，彭昭鸿2，黎旦1，李利彬1，高艺成1

（1.哈尔滨工程大学 智能科学与工程学院，黑龙江 哈尔滨 150000； 2.青岛哈尔滨工程大学创新发展中心，山东 青岛 266000）

针对Informed-RRT(rapidly-exploring random tree)*算法收敛速度慢、优化效率低和生成路径无法满足实际需求等问题，开展了基于MI-RRT* (Modified Informed-RRT*)算法的路径规划研究，通过引入贪心采样和自适应步长的方法提高算法的收敛率，减少路径生成时间、降低内存占用；利用最小化Snap曲线优化的方法使路径平滑的同时动力也变化平缓，达到节省能量的效果，并提供实际可执行的路径。最后通过多组不同复杂度的实验环境表明，较Informed-RRT*算法MI-RRT*算法稳定性更高、所得规划路径平滑可执行，并且能够减少20%的迭代次数和25% 的搜索时间，得出在开阔以及密集环境中MI-RRT*算法较Informed-RRT*和RRT*算法有明显的优势。

Informed-RRT*算法；贪心采样；自适应步长；MI-RRT*；最小化Snap曲线优化；RRT*算法

0　引言

近年来，随着科技快速发展和机器人技术水平的不断提高，移动机器人、无人飞行器在代替人从事消防救援、庄稼灌溉、餐饮配送、物流分拣等领域得到广泛运用。路径规划作为移动机器人、无人飞行器的一种核心技术，其基本思想是：在给定的初始状态和目标状态下，找出一个路径可行解使得机器人在与障碍物无碰撞的前提条件下从初始状态到达目标状态。路径规划算法有很多，常用的局部路径规划算法有人工势场法［1］、蚁群算法［2-3］、A*算法［4］、遗传算法［5］、粒子群算法［6］等。

在全局路径规划采样算法中，快速随机搜索树算法（rapidly-exploring random tree，RRT）对于解决路径规划问题，有着规划速度快、环境建模要求低、动态环境适应性强等优点，其缺点是搜索时盲目性大、耗时长、计算复杂度高、易陷入死区和存在局部最小值问题［7］。近年来针对RRT算法的改进受到了国内外学者的广泛研究，2011年Karaman Sertac等针对 RRT算法生成路径质量不高、非最优等问题，提出了RRT*算法［8］。RRT*算法继承RRT概率完备性的同时也保证了算法的渐近最优性，但是该算法搜索效率较低，进行较大范围搜索时花费的时间过长；2014年Gammell Jonathan D等针对最优RRT*效率低下，与单一查询性质不一致等问题，提出了Informed-RRT*算法［9］，该方法保持了与RRT*相同的完整性和最优性的概率，并且路径规划能力显著优于RRT*算法；2019年Ryu Hyejeong等针对Informed-RRT*算法在复杂环境中减少计算时间，提出了一种网格图骨架化方法用于生成初始解决方案的改进Informed-RRT*算法［10］，这种方法可以有效获得初始解决方案并提高算法收敛率；2020年张玉伟等针对Informed-RRT*算法在复杂环境重复规划稳定性差、收敛速度慢的问题，提出IBI-RRT*（informed bi-directional RRT*）的路径规划算法［11］，该算法结合树的双向搜索策略加快对状态子集的探索，提高算法的收敛速度；2022年DAI Jun等针对Informed-RRT*在机器人自主导航中生成路径质量差、导航效率低的问题提出运用贪婪算法以及潜在父节点重构的方法实现对Informed-RRT*算法的优化，并运用动态窗口法对改进算法在ROS（robot operating system）平台上进行了仿真实验［12］。针对Informed-RRT* 开阔环境收敛率低、在障碍物附近地生长不具有灵活性，生成的路径没有考虑动力平缓变化且不够平滑等问题，本文提出了MI-RRT*（modified informed- RRT*）算法，通过引入贪心采样的方法提高算法在不同环境下的收敛率，减少了通过复杂采样所增加的时间；运用自适应步长的方法对障碍物周围的采样点进行精确采样，减少采样点以降低内存占用；以及利用最小化Snap曲线优化的方法所得路径平滑的同时动力变化平缓，达到节省能量的效果。

1　基于MI-RRT*路径规划算法设计

1.1　Informed-RRT*原理

Informed-RRT*算法有效地解决了RRT*效率低下、单一查询性质不一致等问题，并保留了RRT*的概率完整性和最优性。无论配置空间的维度如何，Informed-RRT*算法都能够在有限时间内找到近似最优解的可行路径，路径规划能力优于RRT*算法。

图1 　采样状态子集空间

1.2　主要设计思路

Informed-RRT*相较于RRT*算法提高了算法的收敛率、解决了单一查询性质不一致的问题，但仍然有缺陷需要改善：①Informed-RRT*的改进方式是通过缩小采样范围，不断采样使得路径逐渐优化，因此在一些简单环境，或者目标点周围没有障碍物时仍然需要大量采样才能找到最优路径；②Informed-RRT*与RRT算法一样是以固定步长作为生长树进行随机搜索，当步长过大时，在进行障碍物附近的点进行搜索时随机点被舍弃的概率增大，步长过小会导致生长树不能对空间进行高效率的搜索，开阔空旷环境搜索速率降低；③算法生成的路径是通过路径点直接相连，生成的路径不够平滑，这使得在实际情况中很难得到应用。针对Informed-RRT*算法的这些问题，本文提出了MI-RRT（informed bi-directional RRT*）*算法，通过引入贪心采样［13-14］、自适应步长［15］以及最小化Snap曲线优化［16］等方法对Informed-RRT*算法进行改进优化。

1.3　贪心采样与自适应步长

1.3.1贪心采样

贪心采样是一种解决在某些空旷的环境地图中求最优解问题更简单、更迅速的设计技术［13］。该方法的实现原理是以一定几率对目标点进行采样，判断当前节点与目标点之间是否有障碍物，若有则放弃此次采样进行普通采样，若无障碍物则将终点直接作为采样对象，生成可执行的路径。通过这种采样的方式，在目标点与当前点直接可达时，直接将目标点选为下一次采样点，缩短了到达目标点所消耗的大量时间。

图2 　贪心算法改进前后示意图

1.3.2自适应步长

图3 　贪心算法改进前后示意图

Fig. 3 Tree growth near obstacles

图4 　远离障碍物树生长

1.4　最小化Snap曲线优化

1.4.1最小化Snap轨迹生成

Informed-RRT*算法对最后生成的最优路径的轨迹点进行直线连接，没有考虑实际运动物体的动力学模型，这使得搜索得到的路径粗糙，并不符合移动机器人、无人飞行器实际执行情况，因此需要将直线平滑处理。为了使生成的路径能更好地使用曲线拟合的方式进行描述，针对这一情况，MI-RRT*算法使用最小化Snap［16］曲线优化的方法对最后的轨迹点进行了曲线拟合处理。Snap是加速度的二阶导数，将其作为被控量处理相当于最小化角加速度即动力的微分［17］。这种方法能将原直线变得平滑，同时也能使动力变化尽可能地平缓，以达到节省能量的效果。

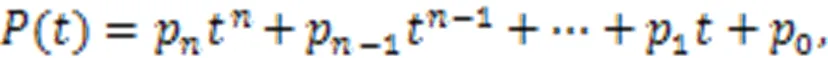
多项式优化中的约束条件被施加在每个路径段的端点上。这些端点在空间中已知位置、速度、加速度。根据相邻点之间的位置、速度、加速度以及相邻点之间需要连续可以构成一个等式约束，合并所有等式约束可变成联合优化问题的一组线性等式约束：

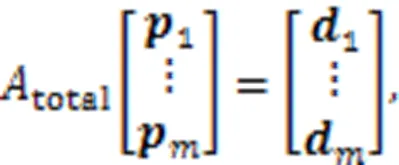
1.4.2通道约束

由于最小化Snap生成的曲线存在凸包现象，为了限制曲线路径和直线的偏离，可以添加通道约束来限制一段路径上的所有控制点都在相应的多维数据集中，由于本次实验仿真在二维环境下进行，因此多维数据集采用控制点向外扩展形成的方形集，当所有控制点都生成一个方形集时，此时曲线产生的凸包一定在所生成的方形集内，这就意味着整个轨迹段被限制在方形集内。通道约束限制方法：

为了实现通道约束需要构建2个不等式约束：

1.4.3时间分配

1.5　算法设计与步骤

图5 　算法流程图

算法1：

下面介绍各个函数功能。

2　仿真校验

为了验证MI-RRT*算法的有效性，本实验采用PyCharm Community Edition 2021.2.1环境下进行路径规划仿真校验，二维实验环境为800×600单位大小的栅格空间地图，通过改变环境中障碍物数量和大小，建立3幅不同的环境地图，Map1为简单地图、Map2为稀疏开阔地图、Map3为密集复杂地图分别对算法可靠性进行验证，地图相关数据如表1所示。

表1 　地图数据

本节通过对比分析RRT*算法、Informed RRT*算法和MI-RRT*算法在3种不同地图环境下运行得出仿真结果。图6～8均是迭代5 000次所得到的结果，图中a）为Informed-RRT*算法在地图中运行得出的路径图，b）为MI-RRT*算法在地图中运行得出的路径图。

图6 　Map1中算法运行结果

图7 　Map2中算法运行结果

图8 　Map3中算法运行结果

对比Map1仿真结果可以看出，Informed-RRT*算法在目标点周围没有障碍物的情况下仍然需要大量的迭代才能得出路径，但MI-RRT*算法在越过障碍物对目标点直接可达时能快速得出路径，因此减少了大量迭代次数，提高了算法收敛率。

在简单开阔地图Map2中，Informed-RRT*算法对开阔环境进行采样时由于步长固定，对采样的次数多，迭代次数随之增加，MI-RRT*在开阔环境进行采样随着距离障碍物的远近选取合适的采样步长，在较少的采样次数下就能到达目标点。

Map3中可以看出，Informed-RRT*算法在采用与图6，7相同步长的情况下仿真出的结果离最优结果相差较大，MI-RRT*算法在采用自适应步长情况下能对狭小空间障碍物附近的点进行采集从而得出趋于最优的路径。对比可以看出，MI-RRT*得出的路径较平滑，具有可执行性，并且由于对Snap优化达到了节省能量的效果。

表2所列为RRT*，Informed RRT*，MI-RRT*在地图Map1，Map2，Map3初次运行得出可行解的具体数据，通过实验数据可以观测出，MI-RRT*相较其他2种算法，在相同地图环境下在初次得到可行解的迭代次数、时间以及路径长度等方面都有性能的提升；同时随着地图环境复杂度的增加，MI-RRT*所消耗时间、迭代次数同样增加，但仍然低于RRT*，Informed RRT*算法消耗时间、迭代次数，并且得出路径长度也优于其他2种算法。表3数据为不同算法在迭代100～5 000次所得路径长度数据图，从不同地图中可以看出，MI-RRT*通过较少的迭代次数就得到趋于最优路径的解，随着迭代次数的增加在前一路径的基础上路径逐渐优化。

图9为RRT*，Informed RRT*，MI-RRT*3种算法在地图Map3收敛情况对比图，从图中可以看出，路径长度随时间变化的趋势图，MI-RRT*与前2种算法相比收敛速度快、所得到的路径短。

表2 　算法初次运行得出可行解数据

表3 　Map1～Map3运行结果数据

图9 　3种算法的收敛情况对比图

综上所述，通过生成路径具体情况，迭代次数，收敛时间等不同方面进行了比较，可以看出3种算法收敛率大小关系为MI-RRT*算法>Informed-RRT*算法>RRT*算法。

3　结束语

本文在Informed-RRT*算法基础上进行改进，提出了一种MI-RRT*算法。通过贪心采样的方法提高了算法的收敛率，减少了复杂采样所增加的时间；采用自适应步长的方法，对障碍物附近的点进行采样，减少采样点降低对采样点存储而占用的内存空间；利用最小化Snap曲线优化的方法使直线平滑的同时达到节省能量的效果。与Informed-RRT*算法相比，MI-RRT*算法稳定性更高，迭代次数方面降低20%、搜索时间方面缩短25%。MI-RRT*能解决在不同环境下的路径规划，但现如今任何一个单独的算法都不足以解决实际问题中的所有路径规划问题，未来可以对多种路径规划算法进行融合达到算法优势互补的目的，以及将路径规划算法扩展到三维空间进行研究。

［1］ KUMAR P B， RAWAT H， PARHI D R. Path Planning of Humanoids Based on Artificial Potential Field Method in Unknown Environments［J］. Expert Systems： The International Journal of Knowledge Engineering， 2019，36（1）：1-12.

［2］ 欧阳志宏，郭强. 改进蚁群算法的无人机突防航路规划［J］. 现代防御技术，2018， 46（1）：74-78，114.

OUYANG Zhihong， GUO Qiang.Improved Ant Colony Algorithm for UAV Penetration Route Planning ［J］. Modern Defence Technology， 2018， 46（1）：74-78， 114.

［3］ 赵玉新，刘利强，李刚. 无人智能运载器航路规划方法及其应用［M］. 北京：科学出版社，2014.

ZHAO Yuxing，LIU Liqiang，LI Gang. Route Planning Method of Unmanned Intelligent Vehicle and Its Application ［M］. Beijing： Science Press，2014.

［4］ 孔慧芳，盛阳. 基于改进A算法的AGV路径规划研究［J］. 现代制造工程，2021 （10）：60-64.

KONG Huifang，SHENG Yang.Research on AGV Path Planning Based on Improved Aalgorithm ［J］. Modern Manufacturing Engineering， 2021 （10）：60-64.

［5］ LAMINI C， BENHLIMA S， ELBEKRI A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning［J］.Procedia Computer Science， 2018：180-189.

［6］ SONG Baoye， WANG Zidong， ZOU Lei. On Global Smooth Path Planning for Mobile Robots Using a Novel Multimodal Delayed PSO Algorithm ［J］. Cognitive Computation， 2017（1）：5-17.

［7］ 霍凤财，迟金，黄梓健，等.移动机器人路径规划算法综述［J］. 吉林大学学报（信息科学版），2018 （6）：639-647.

HUO Fengcai，CHI Jin， HUANG Zijian， et al. A Survey of Path Planning Algorithms for Mobile Robots ［J］.Journal of Jilin University （Information Science Edition），2018（6）： 639-647.

［8］ KARAMAN S， FRAZZOLI E. Sampling-Based Algorithms for Optimal Motion Planning ［J］. International Journal of Robotics Research， 2011（7）：846-894.

［9］ GAMMELL J D， SRINIVASA S S， BARFOOT T D. Informed RRT*： Optimal Sampling-Based Path Planning Focused via Direct Sampling of an Admissible Ellipsoidal Heuristic ［C］∥IEEE/RSJ International Conference on Intelligent Robots and Systems， 2014：2997-3004.

［10］ RYU H， PARK Y. Improved Informed RRT* Using Gridmap Skeletonization for Mobile Robot Path Planning ［J］. International Journal of Precision Engineering and Manufacturing， 2019（11）：2033-2039.

［11］ 张玉伟，左云波，吴国新，等. 基于改进Informed-RRT*算法的路径规划研究［J］. 组合机床与自动化加工技术，2020 （7）：21-25.

ZHANG Yuwei，ZUO Yunbo， WU Guoxing， et al. Research on Path Planning Based on Improved Informed-RRT* Algorithm ［J］.Combined Machine Tools and Automated Processing Technology，2020 （7）：21-25.

［12］ DAI Jun， LI Dongfang， ZHAO Junwei， et al. Autonomous Navigation of Robots Based on the Improved Informed-RRT* Algorithm and DWA ［J］. Journal of Robotics， 2022，2022：1-9.

［13］ 代军，李志明，李艳琴，等. 基于改进Informed-RRT*算法的机器人路径规划［J］. 河南理工大学学报（自然科学版），2021（1）：1-11.

DAI Jun，LI Zhiming，LI Yanqin， et al. Robot Path Planning Based on Improved Informed-RRT* Algorithm ［J］.Journal of Henan University of Technology（Natural Science Edition）， 2021（1）：1-11.

［14］ 朱奕航. 四旋翼无人机路径规划及跟踪控制技术［D］.南京：南京航空航天大学，2020.

ZHU Yihang. Four-Rotor UAV Path Planning and Tracking Control Technology ［D］. Nanjing： Nanjing University of Aeronautics and Astronautics，2020.

［15］ 陈晋音，施晋，杜文耀，等. 基于MB-RRT*的无人机航迹规划算法研究［J］. 计算机科学，2017 （8）：198-206.

CHENG Jinyin，SHI jin， DU Wenyao， et al. Research on UAV Track Planning Algorithm Based on MB-RRT* ［J］. Computer Science， 2017 （8）：198-206.

［16］ MELLINGER D， KUMAR V. Minimum Snap Trajectory Generation and Control for Quadrotors ［C］∥2011 IEEE International Conference on Robotics and Automation. Shanghai，China： IEEE International Conference on Robotics and Automation （ICRA 2011），2011： 2520-2525.

［17］ 韩晓微，刘宏宇，石泽亮，等. 移动机器人最小化snap与A*的联合轨迹优化［J］. 沈阳大学学报（自然科学版），2021 （4）：321-327.

HAN Xiaowei，LIU Hongyu， SHI Zeliang， et al.Joint Trajectory Optimization of Minimizing Snap and A* for Mobile Robots ［J］. Journal of Shenyang University（Natural Science Edition）， 2021 （4）：321-327.

［18］ RICHTER C， BRY A， ROY N. Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments［C］∥Proceedings of the 16th International Symposium on Robotics Research （ISSR）， 2016： 114， 649-666.

Research of Path Planning Based on MI-RRT*Algorithm

YUQiang1，2，PENGZhaohong2，LIDan1，LI Libin1，GAOYicheng1

（1.College of Intelligent Systems Science and Engineering， Harbin Engineering University， Harbin 266000， China； 2.Qingdao Innovation and Development Center of Harbin Engineering University， Qingdao 266000， China）

Aiming at the problems of the Informed-RRT（rapidly-exploring random tree）* algorithm， such as slow convergence speed， low optimization efficiency and inability to execute the generated path， path planning research based on MI-RRT* （modified informed-RRT*） algorithm is carried out. The method of greedy sampling and adaptive step size is introduced to improve the convergence rate of the algorithm， reduce the path generation time and the memory usage. Minimum Snap curve is used to make the path smooth and the power change smoothly， so as to achieve the effect of saving energy and the path to generate the executable. Several sets of different experimental environments are run to show that the MI-RRT* algorithm is more advantageous than the original algorithm， the resulting planned path is smooth executable and it can reduce the number of iterations by 20% and the search time by 25%. Compared with the open and dense environment， the MI-RRT* algorithm has obvious advantages over the Informed-RRT* ，RRT* algorithms.

Informed-RRT*（rapidly-exploring random tree） algorithm；reedy sampling；adaptive step size；modifiend informed-RRT*（MI-RRT*）；minimum snap；RRT* algorithm

10.3969/j.issn.1009-086x.2023.04.015

TP301.6；TP391.9

A

1009-086X（2023）-04-0116-10

于强, 彭昭鸿, 黎旦, 等.基于MI-RRT*算法的路径规划研究[J].现代防御技术,2023,51(4):116-125.

YU Qiang,PENG Zhaohong,LI Dan,et al.Research of Path Planning Based on MI-RRT* Algorithm[J].Modern Defence Technology,2023,51(4):116-125.

2022 -06 -21 ;

2022 -12 -06

于强(1977-)，男，辽宁省东港人。讲师，博士，研究方向为陀螺仪及导航技术、航行器路径规划、磁探测等方面。

266000 山东省青岛市黄岛区哈尔滨工程大学青岛创新发展基地 E-mail：yuqiang@hrbeu.edu.cn