基于贝叶斯网络的高速公路交通事故严重程度预测及致因分析

成 卫,马铭炜,张小龙

(1. 昆明理工大学 交通工程学院,云南 昆明 650504; 2. 通号智慧城市研究设计院有限公司,北京 100071)

0 引 言

随着我国高速公路的不断发展,截至2020年底,中国高速公路总里程已达16万km,位居全球第一。高速公路运输已经成为我国陆运的主要手段。同时,伴随着我国汽车保有量的逐年增长,高速公路交通负荷指数上升,导致高速公路的行车风险大大增加,严重影响交通安全,作为承载快速运动和大交通流的道路载体,其交通安全问题是交通管理的核心问题之一[1]。面临如此严峻的高速公路安全[2]形势,有必要通过分析事故数据,调查事故严重程度与其相关风险因素之间的关系,构建事故严重程度预测模型。通常,事故严重程度被认为与一系列风险因素(人、车、道路、环境)相关。了解这些影响因素如何导致事故严重程度的增加,有助于探索伤害模式并能够基于例证来改进安全措施,为交管部门制定事前安全预防措施提供理论依据,为其事后启动应急预案提供技术依据,加快事故响应速度,减小事故发生带来的后时空影响。

近年来,对于交通事故影响因素的研究成为学者们关注的重点,从“人-车-路-环境”出发,多维度、多角度地研究交通事故影响因素和事故严重程度的关系对于交通安全有重要的研究意义。针对事故影响因素研究方面,裴玉龙等[3]从道路因素出发,分析了道路平面、纵断面、横断面和交叉口在不同参数设置下对交通事故的影响;李文权等[4]利用国内外交通事故数据对事故发生的时间分布规律方面进行了研究,首次从科研、教育、管理和工程措施方面对交通安全提出建议;赵金宝等[5]研究了车辆类型、事故地点和交通参与者等因素对道路交通事故的影响。但是上述研究未对事故严重程度进行预测。在事故严重程度致因研究方面,马壮林等[6]基于Logistic回归模型研究了交通动态情况、隧道情况和时间等因素对交通事故严重程度的影响,为回归模型在事故严重程度预测领域奠定了基础;K. BUCSUHZY等[7]研究了人为因素对事故严重程度的影响,包括了交通参与者的身心状况、驾驶行为、不同年龄等因素;L. N. LIYANAGE等[8]研究了驾驶者年龄、性别和是否饮酒等方面对事故严重程度的影响;R.TAMAKLOE等[9]对不同路面和光照条件在工作日和周末发生交通事故的严重程度进行了对比分析;戢晓峰等[10]基于有序Logit建立了平纵组合路段事故严重程度识别模型。但这些研究从单一维度出发,受限于利用少量候选预测因子和关注特定问题。因此,需要使用包括大量变量的更全面的数据集,以揭示不同影响因素之间潜在的耦合关系。对于多因素方面的研究,MA Zhengjing[11]等综合多种影响因素构建了交通事故严重程度预测深度学习模型;WEN Huiying等[12]建立了随机效应广义有序probit模型,针对云南山区高速公路,分析了驾驶员性别、年龄、天气情况、车辆类型、交通量等因素对两类驾驶员事故严重程度的影响; 贺玉龙等[13]从事故信息中筛选出7项重要指标建立了基于未确知测度理论的高速公路交通安全评价模型,以此评价路段危险程度;刘海珠[14]采用累积Logistic回归模型研究了15个影响因素对交通事故严重程度的影响;陈昭明等[15]建立了基于混合Logit模型的高速公路交通事故严重程度分析模型,研究了35种变量对事故严重程度的影响,取得了很好的效果。但是大多研究没有考虑到数据的缺失和不平衡问题。

综上所述,大多学者对交通事故影响因素的研究主要从单一因素入手(例如特定事故、特定道路、特定环境条件等),主要原因可能是为了创建一组同质性数据,便于研究,仅少数研究考虑了多种因素的影响。但由于部分因素(交通参与者的性别、年龄对事故严重程度是否有显著影响)还存在争议,且事故变量随机性较强,不同路段不同情况下相同变量也存在异质性(例如驾驶员年龄这一因素在不同事故中表现出不同程度的影响)[16]。另外,现有研究大多集中在二项式事故严重程度上,这也会限制从数据中提取有用信息。针对这些情况,建立合适有效的事故预测模型是越来越多学者研究的目的。

为了综合考量多种因素对高速公路交通事故严重程度的影响,同时考虑到机器学习方法容易造成过拟合问题和变量的异质性问题,笔者采用优于传统贝叶斯方法的树增广型贝叶斯方法构建网络模型,再结合专家知识优化模型网络(即数据融合法),对事故数据进行研究,建立事故严重程度预测模型,找出事故主要致因并进行推理分析,为交管部门作出相应安全决策提供支撑。

1 树增广型贝叶斯网络

贝叶斯网络是一种基于概率论的能够很好地表示各个因素之间关系的图形化网络,是由若干父节点和子节点以及它们之间的有向链接组成的有向无环图(directed acyclic graph,DAG)。贝叶斯网络通过条件概率表达变量之间的影响关系,适用于解决多种不确定性问题,是目前用于推理领域最有效的理论模型之一。树增广型贝叶斯方法(TAN)优于传统贝叶斯方法,它提供了一个类似树的模型。传统贝叶斯方法认为,除目标变量外其他所有变量是互相独立的,用该假设限制网络模型,而实际应用中,不同变量之间并不是相互独立的。树增广型贝叶斯方法考虑的子节点之间可能的影响关系,比传统方法,其具有良好的鲁棒性及更高的准确率。如图1,在树增广型贝叶斯网络中,节点C为节点a1、a2、a3的父节点,由有向边相连。此外,a1、a2、a3之间由有向边相连并形成树,节点ai到节点aj之间的有向弧表示输入变量ai对输出变量C的影响作用不仅取决于变量自身,还取决于变量aj。自变量之间有互相的影响依赖关系,被称为互信息,互信息函数可以由式(1)进行计算:

图1 贝叶斯网络Fig. 1 Bayesian network

(1)

1.1 结构学习

贝叶斯网络的结构学习[17]主要有3种方法:

1)专家经验法。基于专家知识和经验,结合研究对象本身确定贝叶斯网络的节点,综合专家打分情况确定网络结构。其缺点是网络结构缺乏样本数据进行分析对照,有效性稍有欠缺。

2)数据驱动法。包括条件独立和搜索评分两种方法,通过算法对事故样本数据集进行学习,发现变量间的依赖关系,从而建立符合样本集的网络结构。其缺点是对样本数据集要求较高,需要完备且真实的数据集。变量多时,计算比较复杂,消耗时间长且得到的结果不够精确,无法准确反映变量之间的真实依赖关系,存在不符合建模和实际经验的节点。

3)数据融合法。基于前两种方法的结合,能很好地弥补前两种方法的缺点,得到的网络结构能够很好地反应变量之间的关系,在保证有效性的同时又能与数据集相互对照,模型真实且可靠。笔者采用数据融合法进行贝叶斯网络的结构学习,因数据集较为完整,采用搜索评分法寻找评分最优的网络结构,评分函数利用BDeu评分,网络结构寻优用爬山算法进行搜索。基于搜索评分的方法将贝叶斯网络的结构学习看作一种组合优化的问题,通过确定网络结构的评分函数,利用算法搜索寻找最优网络结构,可定义为优化模型:

M=(G,Ω,F)

(2)

式中:G为样本数据集D中所有变量间可能的连接关系的网络结构集;Ω为组合优化过程中需要满足的约束条件集;F为评分函数。

当M为最大值时,得到的网络结构即为最优网络结构。

评分函数有两大类:一是基于贝叶斯的评分函数,主要包括BD评分、K2评分[18]、BDeu评分等;二是基于信息论的评分函数,主要包括MDL评分、AIC评分、MIT评分等。笔者采用基于贝叶斯的评分函数,该方法将寻优过程看作一个MAP(最大后验概率估计)问题:

(3)

式中:P(G|D)为后验概率;G*为最优结构。若G的先验概率为P(G),根据贝叶斯公式得:

(4)

P(G,D)=P(D)P(G|D)=P(G)P(D|G)

(5)

因为P(D)是已知的,与P(G)无依赖关系,则P(G|D)可转换为:

logP(G,D)=logP(D|G)+logP(G)

(6)

最优网络结构可表示为:

G*=arglogP(D|G)+logP(G)

(7)

对式(4)两边取对数可得到:

(8)

式中:P(D|G,θG)为模型关于数据的似然函数L(G,θG|D)。假设模型参数的先验分布P(θG|G)服从参数为aijk的Dirichlet分布,在给定样本数据集D后,得到BD评分:

(9)

当结构的先验分布为均匀分布时,logP(G)=0。假设参数aijk=1,则BD评分转化为K2评分:

fK2(G,D)=logP(G)+

(10)

fBDeu(G,D)=logP(G)+

(11)

1.2 参数学习

通过对给定的贝叶斯网络结构进行参数学习,量化节点之间的影响关系,确定各节点变量的条件概率分布(CPD),输出条件概率分布表(CPT)。参数学习方法主要包括极大似然估计法和贝叶斯估计法。笔者采用贝叶斯估计法算出后验概率,该方法考虑了先验知识的影响,相比于极大似然估计法,其合理性更强。贝叶斯估计法基于贝叶斯原理,根据样本数据及贝叶斯公式计算出后验分布,即参数学习结果。首先取θ表示所有参数组成的向量,P(θ)为θ的先验分布,给定一个样本数据集D,则参数θ的后验概率可以表示为P(θ|D)。为了减少计算的复杂程度,笔者采用Dirichlet分布,利用贝叶斯公式推理,后验概率P(θ|D)为:

(12)

(13)

2 模型应用及结果分析

2.1 数据来源及处理

收集曲靖市境内沪昆高速公路段2017—2019年的1 939起交通事故报告数据,剔除无效数据后,保留有效的1 500起高速公路交通事故数据进行研究。研究因变量为事故严重程度,将其按事故后果分为3类:轻微事故、一般事故、重大事故,分别赋值为1、2、3(因无特大事故,所以不进行单独分类研究),如表1。根据数据分析筛选得到19个高速公路交通事故严重程度的影响因素,将其作为自变量进行研究,如表2。但是实际数据中一般事故有1 038起,占比69.2%,导致数据样本分布极不均衡。为保证输出结果的合理性和真实性,采用SMOTE过(欠)采样算法对事故数据样本进行均衡处理,将处理后的数据进行随机排列,并按照3∶1划分训练集与测试集,用于后续的贝叶斯网络模型计算,总体层次结构如图2。

表1 模型因变量设置及离散化取值Table 1 Setting and discretization value of model dependent variable

表2 模型自变量设置及离散化取值Table 2 Setting and discretization value of model independent variable

图2 模型构建及结果分析层次结构Fig. 2 Hierarchical structure diagram of model construction and result analysis

2.2 结构学习结果

基于笔者收集的样本信息充足,能够较好地体现影响因素之间的关系,采用BDeu评分法进行评分,后用爬山算法进行搜索,寻找评分最优的网络结构。初步得到的网络结构如图3,该网络中明显有不符合常识和专业知识的部分及无关节点,此时利用卡方检验筛选特征工程,并结合专家知识进行数据融合处理。基于初步网络再对各个变量节点关系进行重新构建及排序,除去不符合建模经验的节点及有向连接,剔除孤立的无关节点,得到最终的贝叶斯网络,如图4。其中由特征工程的筛选结果可知,对于事故严重程度这一变量来说,对其影响最大的是特征1(天气情况);其次是特征2(视距情况);最后是特征3(路面情况)。直接影响事故严重程度的5个变量及其特征如表3。

表3 特征工程筛选结果Table 3 Future engineering screening results

图3 初步贝叶斯网络Fig. 3 Preliminary Bayesian network

图4 高速公路交通事故严重程度贝叶斯网络Fig. 4 Bayesian network of freeway traffic accident severity

经过优化的贝叶斯网络保留了13个节点,它们之间的有向连接体现了变量间的相互影响,影响因素囊括了人、车、路、环境4个大类,事故严重程度的主要致因在贝叶斯网络中得到了充分体现。由图4可以看出,天气情况、视距情况、路面情况、事故车辆数和车辆行驶方向这5个因素对事故严重程度有直接影响,其中天气情况(X15)影响效果最为显著,既直接影响了事故严重程度,又间接影响了驾驶员的视距情况和路面情况等其他因素。

2.3 参数学习结果

根据结构学习的结果,笔者可以对网络中的多种变量进行参数学习。根据互信息函数计算输出具体参数学习结果。由于数据量较多,只列出当车辆事故数、天气情况、视距情况取值均为1时事故严重程度的条件概率分布(表4),即当事故车辆数、天气情况、视距情况、路面情况、车辆行驶方向离散化取值均为1时,事故严重程度取值为1(轻微事故)的概率为0.243 71,取值为2(一般事故)的概率为0.756 21,取值为3(重大事故)的概率为0.000 07,其余项以此类推。

表4 事故严重程度的参数学习结果Table 4 Parametric learning results of accident severity

2.4 预测结果及有效性验证

为了验证贝叶斯网络模型的有效性,对训练集和测试集进行对比,如图5。同时,输出模型在测试集上的混淆矩阵,模型命中率如图6。由图6可知:对事故严重程度真实值为1且预测值亦为1的有94个,预测值为2的有27个,预测值为3的有0个;对第1类轻微事故预测的准确率为77.68%,对第2类一般事故预测的准确率为74.19%;对第3类重大事故预测的准确率为100%。再将实际概率与后验概率进行误差分析,通过分析对比发现,轻微事故、一般事故、重大事故的概率分布最大绝对误差分别为0.000 04、0.000 04、0.000 06,如图7～图9。再通过参数学习模型对测试数据集进行测试,准确率约为84.27%。G.F.COOPER等[19]指出, 当模型正确率达到80%以上就认为该模型预测效果良好。同时,与传统贝叶斯方法相比,该模型有更好的准确率和更低的误分类率,如表5。综上说明,该模型有效性验证良好。

表5 模型比较Table 5 Model comparison

图5 事故严重程度预测值与真实值对比Fig. 5 Comparison between the predicted value and the true value of accident severity

图7 轻微事故的误差分布Fig. 7 Error distribution of minor accidents

图8 一般事故的误差分布Fig. 8 Error distribution of general accidents

图9 重大事故的误差分布Fig. 9 Error distribution of major accidents

3 高速公路事故主要致因推理分析

3.1 天气情况对事故严重程度的影响

天气情况对事故严重程度的影响最大,且间接影响范围最广。根据事故报告可得出,在雨、雪天气情况下,路面受到影响变得湿滑,不利于高速行车,驾驶员的视距也会受到严重影响,恶劣情况下还会影响驾驶员的心理素质,进而对驾驶行为造成一定程度的干扰,导致了交通事故的发生。由于路面情况较差,事故发生时驾驶员会完全失去对车辆的掌控,失控车辆的滑动轨迹也不同于正常情况,这样的情况下极容易发生重大、特大事故。天气情况与事故严重程度的关系如图10。由图10可知,雨雪天气更容易造成重大事故的发生。

图10 天气情况-事故严重程度分布Fig. 10 Weather conditions-distribution of accident severity

3.2 视距情况对事故严重程度的影响

驾驶员在高速行车时,由于车速较快,在视距情况受到干扰时,无法对前方路况进行很好地判断,操作反应时间大大缩短,往往在察觉到危险情况时已经来不及避让,从而发生较为严重的事故。视距情况与事故严重程度的关系如图11。由图11可知,重大事故在视距情况较差时更容易发生。

图11 视距情况-事故严重程度分布Fig. 11 Sight distance-distribution of accident severity

3.3 路面情况对事故严重程度的影响

路面情况作为主要致因之一,其影响主要在于干扰了车辆的行驶状态,间接干扰了驾驶员的操作行为,使车辆失控而发生交通事故。路面情况与事故严重程度的关系如图12。由图12可知,路面情况较差时往往有重大事故发生。

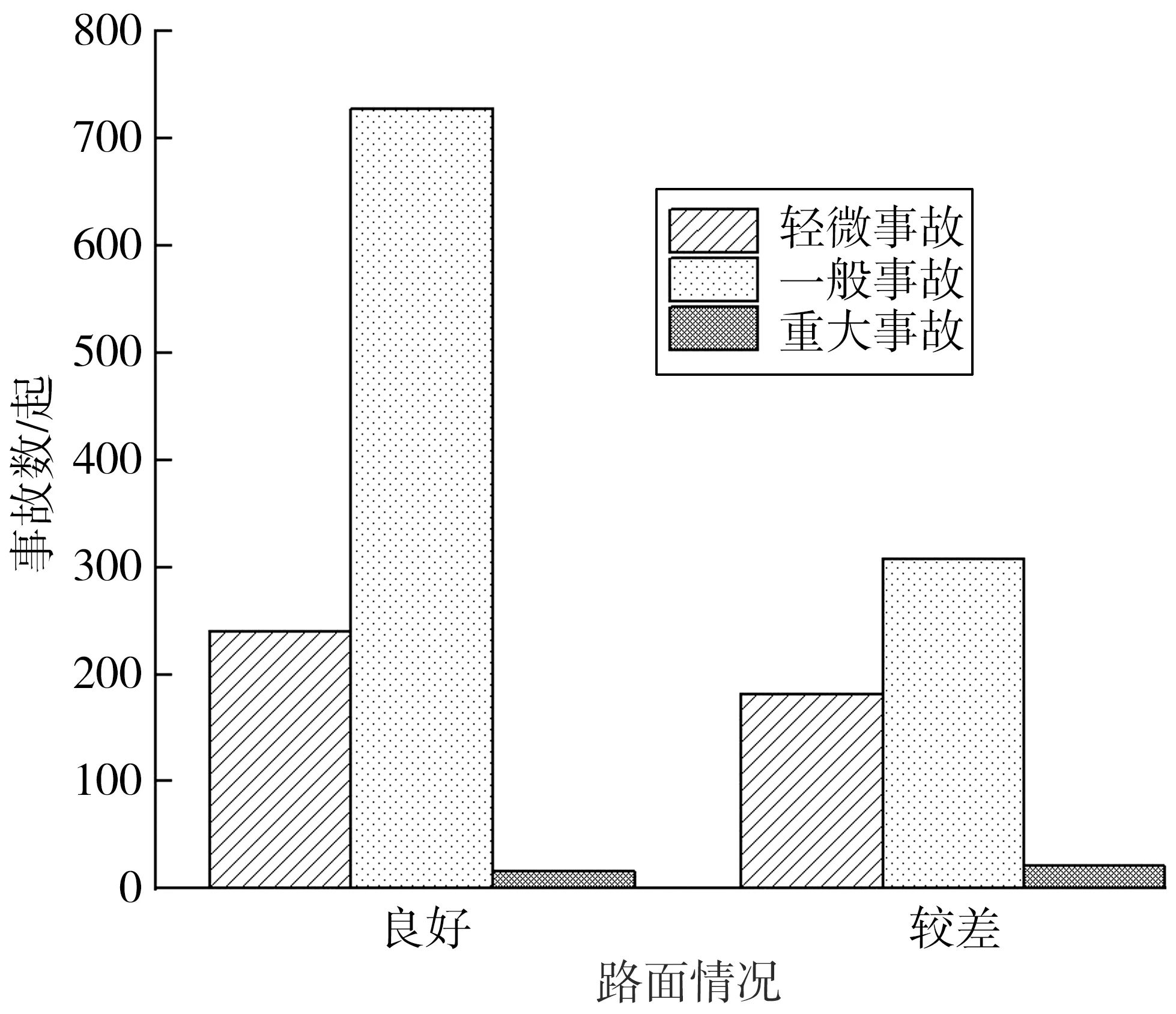
图12 路面情况-事故严重程度分布Fig. 12 Pavement condition-distribution of accident severity

4 结 论

1)高速公路交通事故的发生受到人-车-路-环境这一复杂系统的影响,事故影响因素之间均存在一定依赖关系。通过收集大量的高速公路事故案例进行研究,基于贝叶斯网络构建了考虑多因素下的高速公路交通事故严重程度预测模型。与传统贝叶斯模型相比,树增广型贝叶斯模型对高速公路交通事故严重程度的预测准确率可达84.27%,能够很好地预测高速公路交通事故严重程度,模型通过验证具有良好的准确率,有很好的可靠性。

2)贝叶斯网络推理结果表明,影响高速公路交通事故严重程度的主要致因依次为天气情况、视距情况、路面情况。围绕这几个主要致因,交管部门可以据此完善和改进高速公路的安全策略,有针对性地采取措施,例如在事故多发路段前的LED屏警示驾驶者;对关键路段进行实时监控;定时路段巡逻,观察路面情况并及时清障;在夜间驾驶视距不好的路段加装路灯及反光提示标志,保证高速公路行车安全。在事故发生后及时准确地判断事故严重程度情况,有针对性的采取救援措施。从驾驶者的角度来说,需要培养综合驾驶素质,定期参加有关高速公路驾驶安全知识的学习培训,训练提高对危险情况的判断能力和反应能力,减少不必要事故的发生;掌握不同情况下的紧急操作,学习自救知识,降低高速公路交通事故的严重程度,保障自身安全。

3)高速公路交通事故由多种因素影响造成。由于研究数据有一定局限性,需要更全面完善的数据支持下一步的研究,考虑更多变量例如驾驶方式、碰撞方式、驾驶人的状态及事故发生前短时间车辆运动轨迹等对事故的影响,或找到更加先进的事故预测模型,进而由事故后预测转变为事故实时预测,再转变为事前预警预测,才符合我国未来智能交通的发展方向。