变幅水位影响下高填方岸坡框架码头结构承载特性研究

贺林林,李志松,赵陈雨,钱 进

(1. 重庆交通大学 河海学院,重庆 400074; 2. 重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074; 3. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074)

0 引 言

三峡库区蓄水以来,库水位调度范围在145～175 m间呈周期性涨落,其中水位波动最大可达到30 m[1-2]。对于存在变幅水位影响的岸坡,水位骤降是影响岸坡失稳的主要影响因素[3-4]。三峡库区受库水位变化而发生的滑坡失稳现象较多,自2003年6月10日起,全库区发生崩塌滑坡4 664个,严重变形滑坡累计674个,且滑坡原因多与库水位升降有明显相关性[5-6]。一方面,库区水位变化增加了高填方岸坡变形的程度,使得嵌入到岸坡内的框架码头结构受到更大的下滑力,进而直接影响结构平台的整体稳定性;另一方面,码头桩基的存在又具有一定的抗滑加固的作用。因此,准确评估高填方岸坡码头结构的稳定性存在一定的难度,开展变幅水位影响下高填方岸坡框架码头结构承载特性分析是非常必要的。

关于变幅水位对岸坡及结构的破坏机理,已有学者开展了一定的研究。汤明高等[7]基于离心模型实验,分析了三峡库区水位升降条件下库岸滑坡的变形特征。王孟超等[8]通过有限元方法研究了水位骤降对岸坡安全系数的影响,结果表明:水位骤降期间岸坡稳定性下降了41%。关于渗透力对岸坡土体的影响,张涛等[9]和仉文岗等[10]分别利用有限元软件研究了水位下降条件下土体渗流状态对库岸边坡的不利影响。然而,变幅水位对岸坡土体的影响不仅是通过改变土体的渗透力,还受到水位循环次数和饱和度的影响。刘小强等[11]通过水岩相互作用试验得到了抗剪强度参数随水位循环次数的关系,进而深入研究了水位循环次数影响下的架空斜坡式码头变形特点;刘新荣等[12]通过试验研究表明库水位涨落会使得岩土体抗剪强度参数产生劣化;王中文等[13],边加敏等[14]针对土体含水量进行了一系列的试验研究,研究表明土体含水量的变化直接影响着土体的抗剪强度参数;D.M.GU等[15]研究了周期性干湿循环作用下含软弱夹层灰岩的强度劣化特性。由此可看,库区岸坡失稳多与岩土体性质,水位升降条件等密切相关。一方面,当岸坡长期处于变幅水位条件时,会改变高填方岸坡土体的性质、强度、结构与状态;另一方面,库水位大幅度升降导致岩土体处于渗流状态、含水率发生变化[16],进而引起结构安全储备不足等问题。但上述研究大多只考虑单一变量影响因素,而水位变化对岸坡的影响是一个极为复杂的过程,考虑单一变量并不能很好的体现出变幅水位对岸坡的实际作用过程。尤其对于高填方岸坡,变幅水位对其承载特性的影响情况更为复杂。

鉴于此,笔者考虑到变幅水位主要通过改变土体饱和度和水位循环次数来改变岩土体的结构及含水量,从而使土体抗剪强度参数产生一定程度的弱化,进而导致结构发生失稳现象。基于已建立的渗透力简化计算方法,结合饱和度及水位循环次数影响下的土体抗剪强度参数弱化规律,建立了变幅水位影响下岸坡稳定性计算方法。然后借助ABAQUS建立高填方岸坡框架码头结构有限元模型,并研究码头结构的受力变形等承载特性。

1 变幅水位下岸坡稳定性计算方法研究

1.1 水位骤降影响下岸坡稳定性简化计算方法

基于刘才华等[17]、贺林林等[18]的研究成果,即对岸坡内任一点的应力状态对比分析,得到水位骤降时可将渗透力对岸坡稳定性的影响简化为抗剪强度参数黏聚力降低的等效关系。并将此等效关系与强度折减法相结合,建立岸坡稳定性简化计算模型,进而建立了水位骤降影响下岸坡稳定性简化分析方法。笔者意图基于该研究成果,建立水位骤降影响下综合考虑土体饱和度与水位循环次数的高填方岸坡框架码头稳定性分析方法。

在文献[18]已建立的简化计算方法中,将水位骤降产生的渗透力作用等效为岸坡土体黏聚力的变化,通过推导得出水位骤降影响下渗透力作用而引起的黏聚力变化值c差计算式(1),则土体原始黏聚力c减去c差,即为考虑渗透力作用影响后土体新黏聚力的值c″,如式(2),然后基于强度折减法得到岸坡稳定性简化计算模型,如式(3):

c差=c′-c=(ξ-1)c

(1)

c″=c-c差=(2-ξ)c

(2)

cm=c″/Fr=(2-ξ)c/Fr

(3)

式中:c差为渗透力作用后黏聚力变化值,kPa;c″为考虑渗透力作用后等效的土体新黏聚力值,kPa;c为土体原始黏聚力,kPa;ξ为等效系数(该数据从文献[18]得到);cm为强度折减后土体实际发挥的黏聚力,kPa;Fr为折减系数;c′为考虑渗透力作用时的黏聚力,kPa。

1.2 考虑土体饱和度影响抗剪强度参数弱化规律

魏志华[19]通过对某港区的通用高填方土石料进行现场土体三轴压缩实验,得到了不同饱和度时填方土体所对应抗剪强度参数,并对实验数据进行了整理分析,得到了表1中饱和度与抗剪强度参数的关系。根据表1分别绘制了填方土体黏聚力、内摩擦角随土体饱和度变化的关系曲线图,如图1、图2。

表1 土体抗剪强度参数与饱和度关系Table 1 The relationship between soil shear strength parameters and saturation

图1 土体黏聚力与饱和度关系曲线Fig. 1 Curve of relationship between cohesion and the saturation of soil

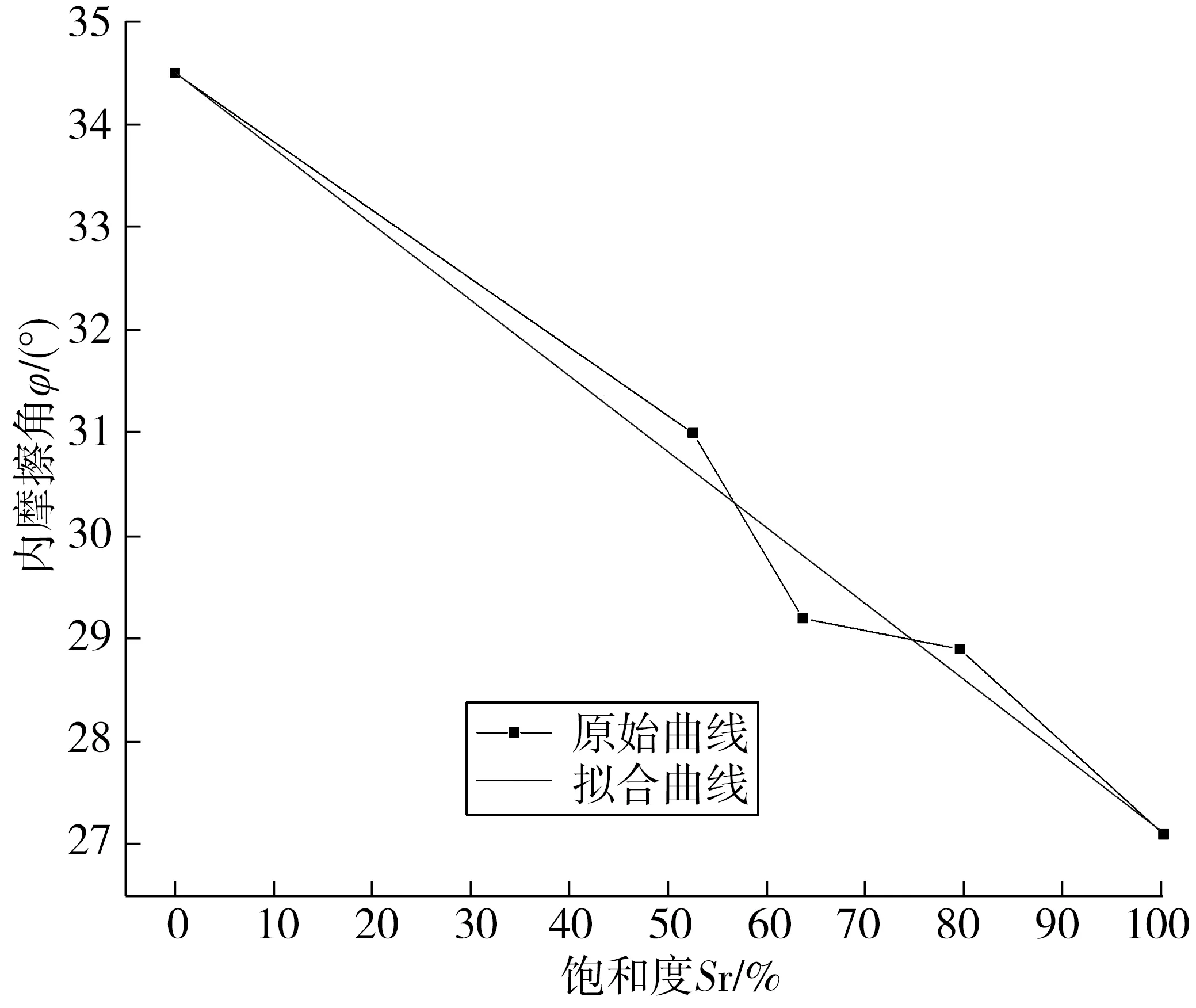
图2 土体内摩擦角与饱和度关系曲线Fig. 2 Curve of relationship between internal friction angle and saturation of soil

通过对上述2条关系曲线进行拟合,得到土体黏聚力、内摩擦角随土体饱和度变化的拟合关系式,如式(4)、式(5):

c=14.73+12.38/(1+e(Sr-0.77)/0.148)

(4)

φ=34.5-7.4Sr

(5)

式中:Sr为岸坡土体饱和度,%;ρ为土体原始内摩擦角,(°)。

基于文献[18]里关于等效系数解法,可求得笔者拟研究的库水位变化渗透力等效系数ξ为1.553,表1中是未考虑水位变化时渗透力对岸坡稳定性影响的土体原始黏聚力值,则可通过式(1)求得水位骤降由于渗透力作用引起的岸坡土体黏聚力变化值c差。计算式(4)可得到考虑土体饱和度影响下的土体黏聚力值,并作为此时土体的原始黏聚力值c减去c差即为考虑渗透力和饱和度影响下的岸坡土体新黏聚力值c″,如表2。根据表2数据,可绘制出考虑渗透力后新黏聚力与饱和度之间的关系曲线,并拟合该曲线如图3。于是,可通过图3中的拟合曲线,得到土体新黏聚力与饱和度之间的关系式,如式(6):

表2 土体新黏聚力c″与饱和度关系Table 2 Relationship between new cohesion c″ and the saturation of soil

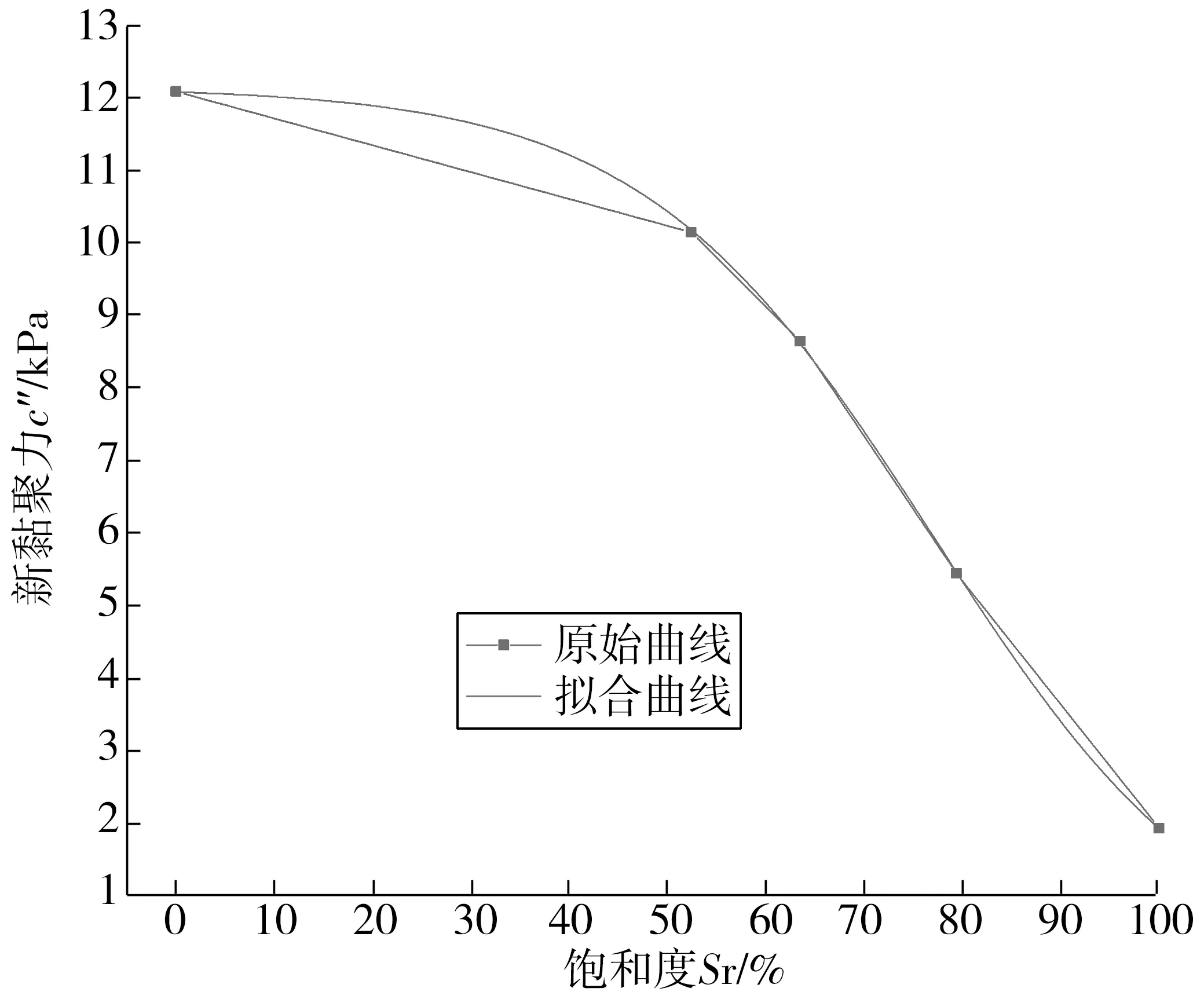
图3 土体新黏聚力与饱和度的关系曲线Fig. 3 Curve of relationship between new cohesion and the saturation of soil

c″=-0.02+12.17/[1+e((Sr-0.763)/0.143)]

(6)

1.3 土体抗剪强度参数受水位循环次数影响弱化规律

高填方岸坡在变幅水位条件下会经受多次干湿循环作用,WANG Junjie等[20]对一种常用于港口土方结构的填方土料进行室内干湿直剪试验,得到了一组适用于港口填方土体的抗剪强度参数随水位循环次数的关系式,如式(7)、式(8)。基于该结论研究建立考虑水位循环变化次数影响的抗剪强度参数弱化规律。

由于水位骤降期间对岸坡的安全影响最大,在研究水位循环次数对岸坡框架码头结构影响的时候,主要考虑水位骤降渗透力对岸坡的作用,因而基于1.1节所述的简化分析方法,则可通过计算式(2)得到考虑渗透力作用后的土体黏聚力值c″0,即为式(7)中未经水位循环的土体初始黏聚力c0,进而可得到考虑渗透力影响后土体非线性抗剪强度参数随水位循环次数弱化的计算式(9)。

c′N=-0.80lnN+c0

(7)

φ′N=-0.36lnN+φ0

(8)

c″N=-0.80lnN+c0″

(9)

式中:c′N为N次水位循环后的土体黏聚力,kPa;c0为土体初始黏聚力,kPa;φ′N为经过N次水位循环后的土体内摩擦角,(°);φ0为土体初始内摩擦角,(°);c″N为N次水位循环后的土体新黏聚力,kPa;c″0为考虑渗透力后未经水位循环的土体初始黏聚力,kPa。

1.4 计算步骤

基于上述1.1节,1.2节,1.3节所论述的研究内容,笔者建立了变幅水位下高填方岸坡框架码头结构承载特性分析有限元计算方法具体步骤为:

1)首先利用ABAQUS有限元软件建立高填方岸坡框架码头计算模型,并对原始土层进行地应力平衡。

2)通过在ABAQUS中材料模块设置场变量来实现考虑土体饱和度、变幅水位循环次数与渗透力共同影响下的高填方岸坡土体抗剪强度参数弱化模型。

3)分别对高填方岸坡框架码头计算模型施加竖向与水平向荷载,进而分析不同饱和度与水位循环次数影响下框架码头结构的竖向与水平向承载性能。

4)最后研究桩土相互作用影响下考虑渗透力后不同饱和度及水位循环次数的岸坡的变形特性分析。

2 有限元计算模型

2.1 工程概况

高填方岸坡框架码头结合工程实际尺寸,通过扩大模拟范围的数值分析验证,考虑边界效应及沿码头结构的纵向对称性,从而综合选取高填方岸坡框架码头尺寸。具体尺寸如下所述,岸坡由下覆基岩和填方土体组成,其中岸坡长度81 m,高度27 m,坡比为1∶3。上部码头结构为六跨三榀框架码头,下部桩基为直径2.4 m的C30钢筋混凝土嵌岩灌注桩,其入土深度分别为14、17 m两种,上部立柱直径为1.5 m。坡顶和坡底分别设置挡土墙,码头结构具体构件及断面设计如图4[21]。材料参数选用某内河实际码头工程,如表3。

表3 模型材料参数Table 3 Model material parameters

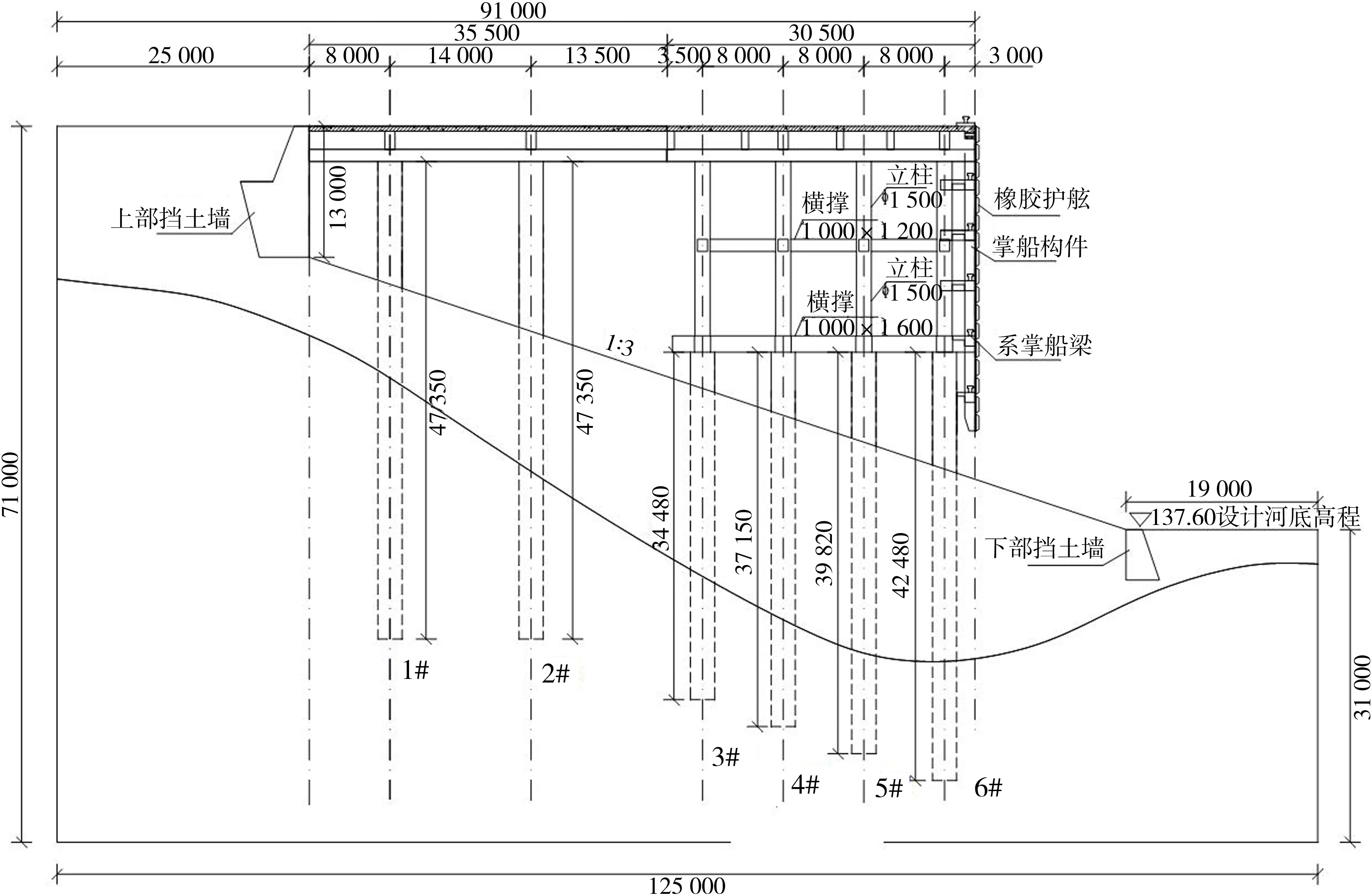
图4 某高填方岸坡框架码头工程断面Fig. 4 Section of a high-filled bank frame wharf project

2.2 有限元模型建立

土体材料采用摩尔-库伦弹塑性本构模型,且应用非对称算法计算。为模拟出饱和度及水位循环次数变化对岸坡土体的弱化过程,在Property版块将黏聚力与内摩擦角分别设置成随饱和度1%～100%、水位循环次数1～100次变化的场变量,计算结果所对应的分析步时间即为此时岸坡土体所处于的饱和度及水位循环次数状态;在initial分析步后设置Geostatic分析步以便地应力平衡,之后设置Static General分析步;然后依据我国JTS 144—1—2010《港口工程荷载规范》其后方陆域设计堆货荷载取60 kPa,前方承台面板设计荷载取50 kPa;岩土体左右侧面设置水平约束(U1=0),前后侧面设置对称约束(U2=0),底部设置铰支约束(U1=U2=U3=0),坡顶挡土墙在右侧设置水平约束(U1=0);桩土接触作用在法向采取硬接触,切向使用罚摩擦系数,浸水后的桩土摩擦系数μ=tan(0.75φ)[22],取0.485,坡顶与坡底的挡土墙与填方土体之间的摩擦系数取0.5[23];岸坡码头结构网格类型均采用C3D8单元。为便于分析从上至下分别为第1至第6排桩基,对中间1榀排架桩基分别标号为1#～6#,如图5。

图5 高填方岸坡框架码头三维几何模型Fig. 5 3D geometric model of a high-filled bank slope frame wharf

3 变幅水位影响下结构有限元计算结果

3.1 考虑渗透力与饱和度影响下码头结构稳定性分析

3.1.1 码头竖向承载特性分析

为进一步分析码头竖向承载特性,需对框架码头结构面板逐级施加竖向荷载,然后选取中间1榀排架1#～6#桩基作为研究对象,从而选取受力最不利桩基,对比分析整个高填方岸坡框架码头竖向承载特性,以确保结果更具代表性。

图6为考虑渗透力作用后饱和度为90%情况下1#～6#桩桩顶沉降曲线图。分析曲线结果:1#～6#桩基Q-S曲线为缓变型曲线无明显拐点,其中1#与2#桩Q-S曲线斜率缓慢增大,可知桩端土体发生弹塑性变形。3#～6#桩Q-S曲线斜率很小,近似直线,属于弹性变形阶段,可看到1#桩基为框架码头受力最不利桩基。分析其原因:一方面,框架码头的刚度远大于周围土体的刚度,且3#～6#桩基由于框架结构横纵撑的约束作用,为3#～6#桩基提供了较强的竖向承载能力,1#与2#桩端上部与上层面板嵌固在一起,其承载能力相对弱于3#～6#桩;另一方面,上部荷载主要通过桩侧摩阻力与桩端阻力传递到下部群桩基础,桩端持力层为抗剪强度参数较强的基岩,可为桩基提供较强的桩端阻力,进一步加强了框架的竖向承载特性。

图6 考虑渗透力后饱和度为90%的1#～6#桩桩顶沉降曲线Fig. 6 Settlement curve of top of piles 1#～6# with saturation of 90% after considering permeability

桩基的破坏特征主要体现在Q-S曲线上,但对于缓变型Q-S曲线时,表现为渐进的破坏趋势,但是破坏节点并不显著,此时需选用其他方式判断桩基极限承载能力,通常采用桩基沉降与位移容许值的判别方式。判别方式的选取:依据相关规范[24]对桩径D大于800 mm的桩,宜选取沉降量S=0.05D时对应的荷载作为桩的极限荷载值,笔者取120 mm作为竖向沉降位移容许值。然后选取1#受力最不利桩基作为研究对象,研究考虑渗透力作用后不同饱和度影响下码头结构竖向承载特性。

图7为考虑渗透力作用后不同饱和度情况下1#桩桩顶沉降曲线图。

图7 考虑渗透力后不同饱和度的1#桩桩顶沉降曲线Fig. 7 Settlement curve of pile top of 1# pile with different saturation after considering permeability

图7中数据表明:当土体饱和度为14%、50%、90%时,Q-S曲线重叠在一起几乎没明显变化,以120 mm为竖向沉降容许值求得饱和度14%、50%、90%时竖向极限荷载分别为1 124.99、1 124.35、1 123.84 kPa,可见饱和度对高填方框架码头竖向承载能力影响甚微。分析其原因:渗透力与饱和度的影响导致岸坡高填方土体抗剪强度参数发生弱化,而桩底持力层为基岩,其抗剪强度参数并不随着饱和度的变化而变化,并且地基对桩的支撑力主要由桩端阻力组成,因此桩端地基的抗剪强度参数决定着整个码头结构的竖向承载能力,故考虑渗透力后饱和度的变化对码头结构竖向承载特性的影响并不显著。

3.1.2 码头水平承载特性分析

同理,为进一步分析码头结构水平承载特性,需对框架码头靠船构件逐级施加水平撞击力,从而选取受力最不利桩基作为研究对象,对比分析整个高填方岸坡框架码头水平向承载特性。桩基水平极限荷载的判别方式:由于框架码头刚度较大,施加水平荷载时会产生挠曲变形,最后使得桩基超过水平位移容许值,达到结构的水平极限荷载。依据相关规范[24],当桩顶水平位移达到30～40 mm可终止加载,拟采用30 mm作为框架码头结构的水平向极限承载力。

图8为考虑渗透力作用后饱和度为90%情况下1#～6#桩桩顶水平位移曲线图。

图8 饱和度为90%的1#～6#桩桩顶水平位移曲线Fig. 8 Horizontal displacement curves of top of piles 1#～6# with saturation of 90%

分析图8曲线结果:一开始未加荷载前1#～6#桩顶位移处于负向位移,然后随着水平撞击力的增大1#与2#桩基桩顶水平位移基本没变化,3#～6#桩基呈线性趋势增大,此时桩基仍处于弹性变化阶段;3#～6#桩基水平位移曲线基本一致,其中6#桩变化趋势稍大于其他桩,说明6#桩为受水平荷载最不利桩基,拟选取6#桩研究不同饱和度影响下框架码头的水平向承载能力。分析其原因:一开始在未施加荷载前由于框架码头结构自重的作用,岸坡土体具有向下滑的趋势,1#～6#桩基受到较大的下滑力导致桩顶产生了负向位移。并且框架码头结构的刚度较大,若要产生挠曲变形需要克服后方土压力的作用,1#和2#桩基抵御了后方岸坡土体较大的土压力并与受到的水平撞击力相互抵消,所以施加的水平荷载大多由3#～6#桩基抵御,因此1#～2#桩桩顶的水平位移基本没变化。

图9为考虑渗透力作用后不同饱和度情况下选取最不利桩基6#桩桩顶水平位移曲线。图9中数据表明:采用30 mm作为码头结构的水平向极限承载力时,土体饱和度为14%、50%、90%影响下6#桩基水平极限承载力分别为3 040.39、3 101.11、3 237.41 kN。饱和度为90%比饱和度为50%水平极限承载能力增加了4.4%,比饱和度为14%增加了6.4%。分析其原因:土体抗剪强度随着饱和度的增加而发生弱化现象,处于岸坡上的填方土体产生了更大的下滑力作用,对框架码头施加水平撞击力则需要抵御更大的岸坡下滑力才能使桩基产生水平变形,因此撞击荷载作用下,土体饱和度的增大相对增大了框架码头水平极限承载能力。

图9 不同饱和度的6#桩桩顶水平位移曲线Fig. 9 Horizontal displacement curve of pile top of 6# pile with different saturation

3.1.3 考虑渗透力与饱和度影响高填方岸坡变形特性分析

图10(a)～图10(c)为考虑渗透力作用后饱和度为14%、50%、100%的岸坡塑性应变云图。由图10可知,饱和度14%时,填方土体与基岩交界面出现了塑性应变,第1、2排桩基周围土体的塑性应变区逐渐向坡面延伸。当饱和度增加至50%时,第2排桩基周围土体与坡面之间形成塑性贯通区。当土体饱和度为100%时,岸坡塑性应变区不断延伸至后方堆载区域,坡顶挡土墙下部与第1排桩基周围土体形成贯通区,坡底周围土体开始出现范围较小的塑性应变。分析其原因:饱和度的增加使得土体抗剪强度参数弱化,因此岸坡塑性应变随着饱和度的增加而增加。但岸坡底部土体由于码头桩基及坡底挡土墙抗滑加固的作用,塑性应变较小。

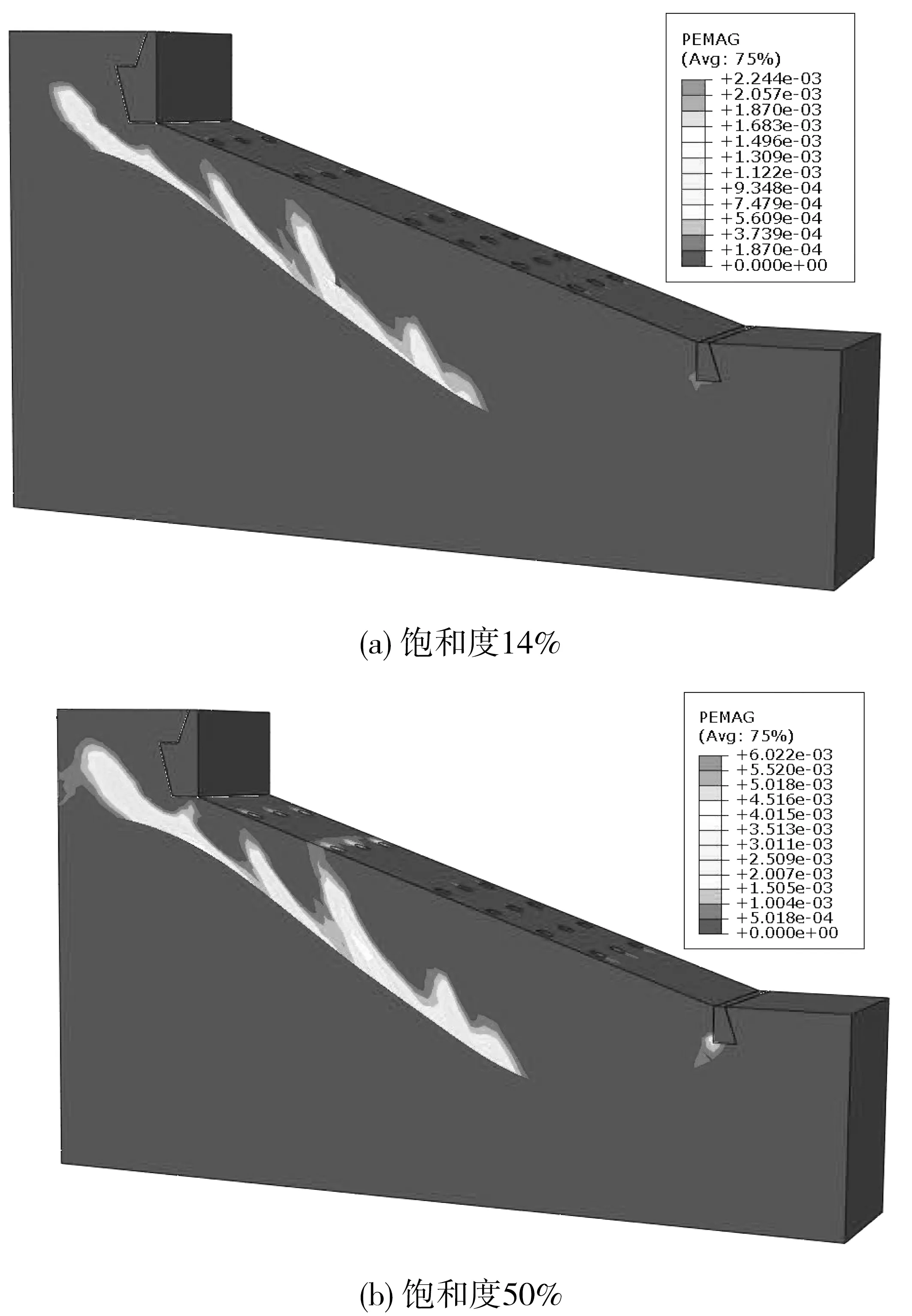
图10 考虑渗透力后不同饱和度的岸坡塑性应变云图Fig. 10 Plastic strain nephogram of bank slope with different saturation after considering permeability

图11为岸坡Path-1路径示意,研究沿Path-1路径位移变化的趋势,可以直观清晰的体现出渗透力及不同饱和度共同作用对高填方岸坡的影响。

图11 岸坡Path-1路径示意Fig. 11 Bank slope Path-1 diagram

图12为饱和度为14%、50%、100%下沿Path-1路径的竖向沉降变化图。

图12 Path-1路径竖向沉降Fig. 12 Path-1 vertical settlement

图12中数据表明:岸坡土体竖向沉降变化最大的区域集中在上部挡土墙、第1排桩基与第2排桩基周围,从第2排桩基到坡底土体的竖向沉降逐渐减小,在其他几排桩基周围处出现轻微的幅度变化,靠近底端位移变化量接近为0,其中第2排桩基位置土体沉降最大;饱和度为14%、50%、100%时第2排桩基竖向沉降分别可达到3.99、11.69、36.84 mm,100%饱和度比14%饱和度时第2排桩基土体沉降增加8.23倍,100%饱和度时比50%饱和度时第2排桩基土体沉降增加2.2倍。

图13为饱和度为14%、50%、100%时随沿Path-1路径的水平位移图。图中所示同一位置同一路径上各点的位移对比曲线,可得知在土体饱和度为14%、50%时Path-1路径水平位移变化较小,饱和度增大到100%时Path-1路径水平位移有大幅度变化,其中变化最大的是坡顶第1排桩基周围区域,第2排桩基周围区域水平位移变化次之,path-1路径越往底部水平位移变化趋势越小,坡底水平位移接近为0。14%、50%和100%饱和度时第1排桩基周围土体水平位移变化量最大分别可达到2.56、6.58、20.31 mm,100%饱和度时其水平位移变化量比14%饱和度时增加6.9倍,比50%饱和度增加2.09倍。分析其原因:桩基及岸坡底端挡土墙的阻挡作用,使得岸坡底部水平位移变化较小,但通过对比分析不同饱和度影响下的岸坡变形可知,饱和度对岸坡位移变形影响较大。

图13 Path-1路径水平位移Fig. 13 Path-1 horizontal displacement

3.2 考虑渗透力与水位循环次数影响码头结构稳定性分析

3.2.1 码头竖向承载特性分析

图14是对框架码头施加竖向荷载并考虑渗透力作用和不同水位循环次数下1#桩桩顶沉降。图14中数据表明:随着竖向荷载的施加,桩顶沉降先呈线性变化趋势后呈非线性变化的趋势,并且不同水位循环次数作用下的Q-S曲线几乎重合,可见水位循环次数的变化对岸坡码头的竖向承载能力并无太大影响;若以桩顶沉降120 mm作为判别方式判断桩基极限承载力,水位循环1、10、100次时1#桩基极限承载力分别为1 124.38、1 124.16、1 123.99 kPa,可见考虑渗透力作用后不同水位循环次数变化对码头结构的竖向承载能力的影响并不显著。分析其原因:桩底持力层是强度很高的岩石并具有较强的嵌固作用,水位循环弱化规律仅适用于填方土体,桩基竖向承载力基本由桩端土体提供,因此水位循环次数变化对码头结构竖向承载能力并无显著影响。

图14 不同水位循环次数的1#桩桩顶沉降Fig. 14 Settlement of pile top of 1# pile with different cycle times of water level

3.2.2 码头水平承载特性分析

图15是对框架码头施加水平撞击力荷载并考虑渗透力作用和不同水位循环次数影响下的6#桩桩顶水平位移曲线图。

由图15可知,随着水平撞击力的增加6#桩桩顶水平位移呈线性增加,水位循环1、10、100次时6#桩桩顶水平位移变化趋势相同,水位循环1次与10次作用对桩基的影响很不明显。采用30 mm作为桩基水平位移容许值,求得水位循环1、10、100次作用下结构的水平极限承载能力分别为3 032.45、3 057.80、3 131.17 kN。其中水位循环100次时高填方岸坡框架码头结构能够承受的水平撞击力荷载比水位循环10次时增加2.4%,比水位循环1次时增加3.3%。

3.2.3 考虑渗透力与水位循环次数影响高填方岸坡受力变形分析

图16(a)～图16(c)是考虑渗透力后水位循环分别为1、10、100次作用下岸坡的塑性应变云图。由图16可知:水位循环1次时,坡面第2排桩基处与岩土交界面形成塑性贯通区,塑性变形区具有向后方陆域堆载区域发展的趋势。水位循环10次时,第1排桩基周围也出现明显的滑动面,岸坡底部未出现明显塑性变形区。随着水位循环逐渐增加至100次时,后方陆域区域开始出现塑性变形,但并未完全贯通,坡顶挡土墙下部相继出现贯通区,坡底塑性应变较小。

图16 考虑渗透力后不同水位循环次数的岸坡塑性应变云图Fig. 16 Plastic strain nephogram of bank slope with different cycle times of water level considering permeability

图17为考虑渗透力后不同水位循环次数沿Path-1路径的竖向沉降图。由图17可知,水位循环次数越大,岸坡竖向沉降越大,Path1路径发生最大沉降的位置集中在坡顶与第2排桩基土体周围区域,其中水位循环1、10、100次最大竖向沉降分别为3.57、6.04、15.85 mm,水位循环100次时最大竖向沉降比水位循环10次增大1.6倍,比水位循环1次增大3.4倍。

图17 Path-1路径竖向沉降Fig. 17 Path-1 Vertical Settlement

图18为考虑渗透力后不同水位循环次数下沿Path-1路径水平位移图。从图18中数据可知,发生最大水平位移处是第1排桩基土体周围区域,水位循环1、10、100次时岸坡最大水平位移分别为2.41、4.14、9.01 mm,水位循环次数100次最大水平位移比10次增大1.2倍,比1次水平位移增大2.7倍。从以上数据对比分析可知,考虑渗透力与水位循环次数作用下岸坡的竖向与水平变形都有着大幅变化,影响着岸坡的稳定性且不容忽视。

图18 Path-1路径水平位移Fig. 18 Path-1 horizontal displacement

4 结 论

1)通过整理对比分析已有的试验数据,得到了考虑渗透力的土体抗剪强度参数随土体饱和度和水位循环次数的弱化规律,建立了变幅水位影响下岸坡稳定性的简化分析方法。

2)考虑渗透力作用后不同饱和度及水位循环次数影响下对码头结构面板逐级施加竖向荷载得到码头结构中间排架1#桩为受力最不利桩基,对靠船构件逐级施加水平向撞击荷载时得到中间排架6#桩为受力最不利桩基。

3)考虑渗透力作用后不同饱和度及不同水位循环次数对岸坡框架码头结构的竖向承载能力并无显著影响。考虑渗透力后土体饱和度为14%、50%、90%影响下码头结构水平向极限承载力分别为3 040.39、3 101.11、3 237.41 kN,90%饱和度比14%饱和度影响下水平极限承载力增加6.4%;水位循环次数1、10、100次作用下结构的水平极限承载力分别为3 032.45、3 057.80、3 131.17 kN,其中水位循环次数100次作用下高填方岸坡框架码头结构能够承受的水平撞击力荷载比水位循环次数1次时增加3.3%。

4)随着土体饱和度和水位循环次数的增加,岸坡的塑性应变越来越大,在坡顶挡土墙下部与第1、2排桩基周围土体区域发生明显的贯通现象。其中,当饱和度为14%、50%和100%时,第2排桩基周围土体竖向沉降变化最大,土体饱和度为100%比饱和度为14%时第2排桩基土体沉降增加了8.23倍;第1排桩基周围土体区域水平位移变化较大,其中饱和度100%时其水平最大位移比饱和度14%时增加6.9倍。水位循环次数1、10、100次影响下,高填方岸坡坡顶与第2排桩基周围土体区域竖向沉降变化较明显,其中水位循环次数100次岸坡最大竖向沉降比水位循环次数1次时增大3.4倍,水平位移变化最大的区域为第1排桩基周围土体区域,水位循环次数100次时岸坡最大水平位移比水位循环1次增大2.7倍。