基于最小割集法的配电网可靠性影响分析
2023-09-08卢迪迪陈俊轶卢依婷
卢迪迪 陈俊轶 卢依婷
摘要:为解决传统配电网可靠性评估方法效率低下的问题,使配电网可靠性的研究更加合理、有效,通过最小割集模型,对配电网可靠性进行评估;同时考虑备用电源的影响、计及元件的检修和负荷点的转移,用RBTS-4的标准算例计算出主馈线在有备用电源和分支保护时可靠性明显增强,验证了最小割集法的有效性。
关键词:最小割集法;配电网;可靠性;影响分析
中图分类号:TM732 文献标志码:A 文章编号:1671-0797(2023)17-0001-04
DOI:10.19514/j.cnki.cn32-1628/tm.2023.17.001
0 引言
随着电力系统规模的扩大和系统的并网运行,有关配电网可靠性的分析变得更加复杂[1]。国内外对于配电网系统可靠性的研究大多以统计分析为主,并建立了有效的可靠性数据信息库和相应的管理体系。比如在传统配电网可靠性影响研究中,朱晓荣等人[2]采用蒙特卡洛模拟法,加快了评估速度,但新能源的并网给评估增加了一定的难度。就此,唐巍等人[3]提出了一种基于停电序列的可靠性解析评估方法,使得算法的精度和速度得到提升,但未能考虑负荷转移的影响。Jooshaki等人[4]提出了一种基于拓扑变量的辐射状和辐射状运行网状配电网可靠性评估数学模型,该方法计算精度高,但也未考虑分布式电源以及负荷转移的影响。传统的解析法、模拟法已逐渐无法解决新时代智能电网可靠性计算效率低的问题,基于上述文献研究,本文提出了一种基于最小割集法的配电网可靠性评估方法,结合负荷点转移、备用电源和计及元件的检修,更好地验证了最小割集法的合理性。
1 最小割集
负荷点的最小割集就是元件的集合,用割集元件组合表示系统故障,只有当元件全部正常运行时,系统方可正常运行,任一割集元件故障均可能导致整个系统无法正常运行[5]。
1.1 配电网等效最小割集模型
配电网结构一般采用图论的方法来进行分析,为节省计算量,本文将计算的状态限制在最小割集内,使每个割集中的元件以并联的方式存在[6-7]。
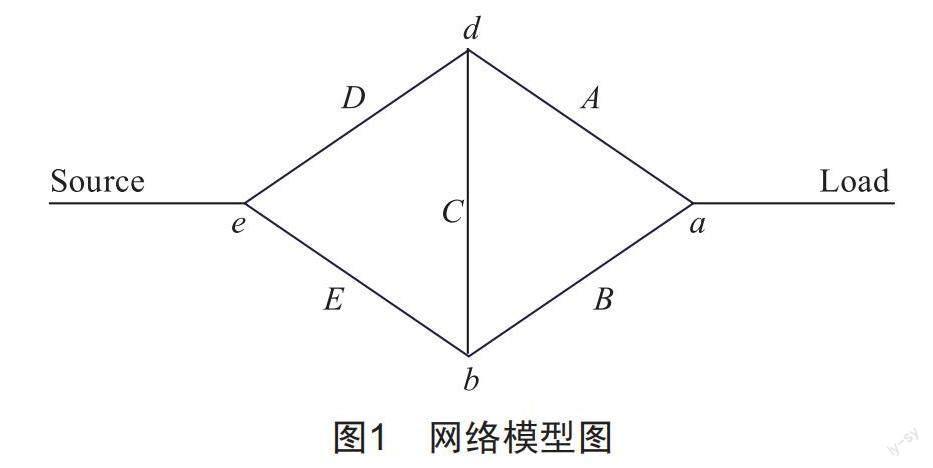
如图1所示,其中最小割集为(A,B)(D,E)(A,C,E)(B,C,D)。
1.2 最小连集及其矩阵
对于复杂的网络,基于遍历搜索的思想,可形成如图2所示的搜索树。
由图2搜索树原理,可得到最小连集及其矩阵。最小连集为(B,E)(A,D)(A,C,E)(B,C,D),连集矩阵为:
1.3 配电网连集向割集的转换
在矩阵T中,一行对应一个最小连集,“1”表示该序列所代表的支路在此连集中,“0”则表示不在此连集中;若一列元素都为“1”,该列为单位向量,该序列代表的元件则为一阶最小割集;若任意两个列向量相加,能够得到类似于一阶最小割集一样的单位列向量,这两个列序代表的元件则为一个二阶割集。
在最小割集矩阵T中,并未有一列均为“1”,由此可得出负荷点无一阶最小割集;这时需将列向量逻辑相加运算得到单位向量,因此负荷点最小二阶割集为(A,B)(D,E);根据逻辑相加运算,同理可得到高阶最小割集。
2 可靠性评估方法
2.1 可靠性评估指标
本文提及的配电网系统可靠性指标,指系统平均停电频率、平均停电时间和平均供电可靠率[8]。
平均停电频率:
式中:∑λa为用户总停电次数;N为用户数(下同)。
平均停电时间:
式中:∑γa为用户停电时间总和(下同)。
平均供电可靠率:
式中:T为时间。
2.2 可靠性评估算法
如图1所示,通过以电源为起点、负荷点为终点的最小割集求取,可把网络结构转变为元件的串联结构。由于高阶割集的非正常运行所引起的故障率相对较小,在现实配电网系统中,最小割集的求取到二阶时就可满足系统可靠性指标要求;二阶割集的元件为并联,所有割集之间近似于串联。
二阶割集的等效年故障率为:
二阶割集的等效年修复时间为:
式中:λi和ri为元件永久性故障率和修复时间。
将年停运率和停运时间累加到负荷点的可靠性指标上,可得到该点失效的所有故障模式[9-10]。
2.3 元件计划检修
在配电网系统中,一般会将2个或3个串联的元件同时停运,此时的检修时间为每个元件检修时间之和。当第1个元件进行计划检修,第2个元件发生故障时,或者第2个元件进行计划检修,第1个元件发生故障时,负荷点是无效的,因此导致的年停运率和停运时间应累加至负荷点的可靠性指标上。
2.4 备用电源及负荷转移
在电力系统中,有关部门会提供许多不同的供電区域,相邻区域之间的负荷转移能力很强,某一区域无法正常运行,相邻区域可将负荷转移,因此,系统中便含有正常电源和备用电源,从备用电源出发可求取备用割集。再将元件的可靠性参数看成矩阵,观察矩阵的行数来判断元件个数,最后计算割集的故障率和停运时间。当元件故障时,负荷转移,故障率不变,停运时间可表示为:
式中:Uplos为停运时间;λt为停运故障率的时间;T为负荷转移的时间。
3 算例分析
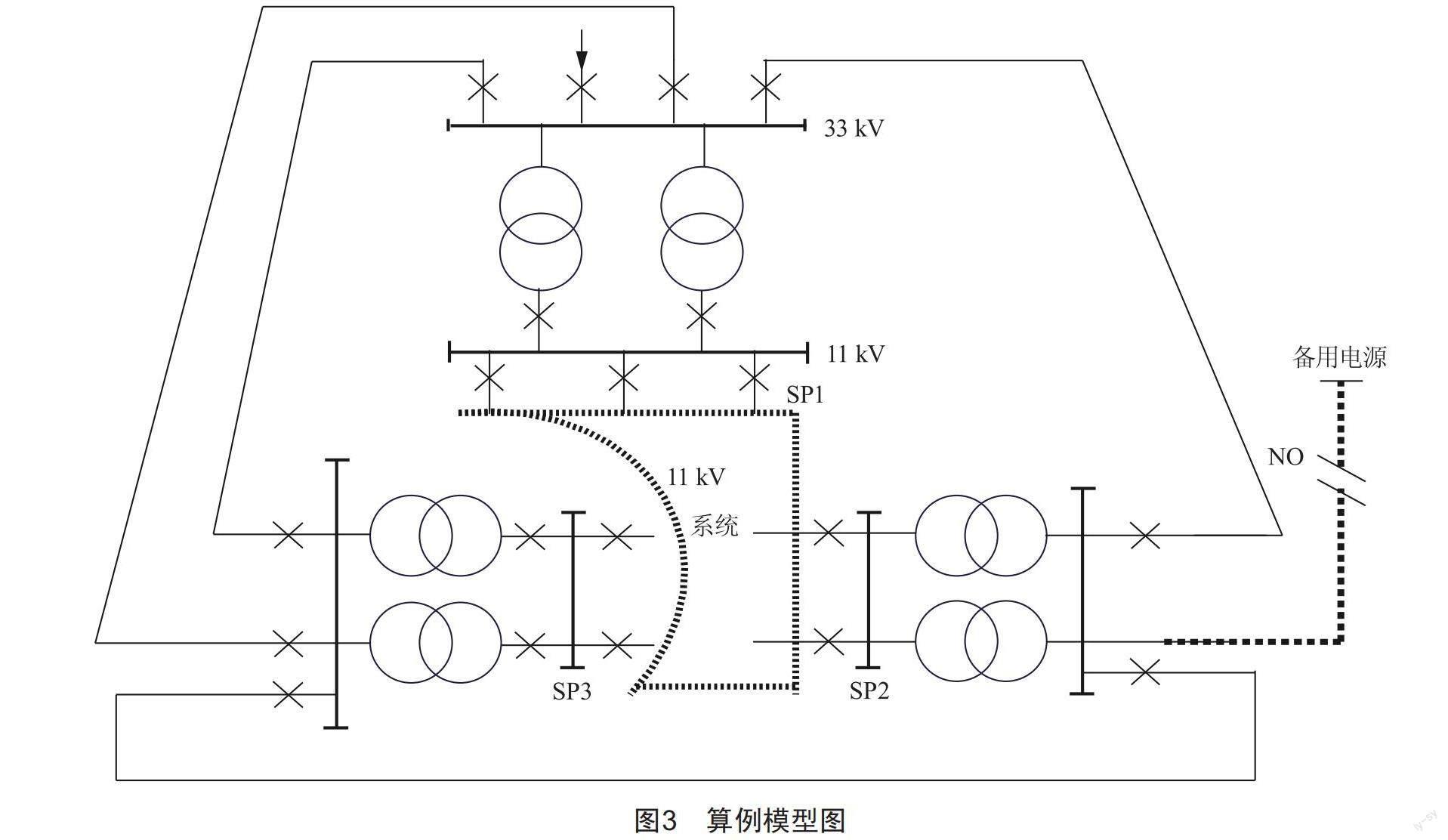
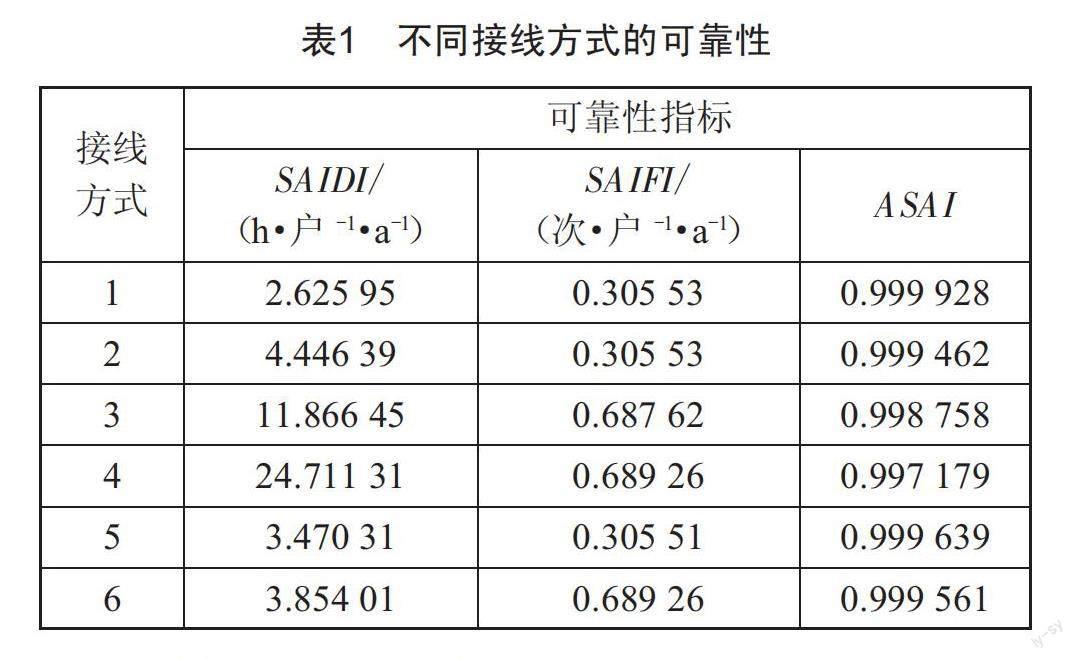
针对本文阐述的配电网可靠性指标和评估方法,结合文献[11-12]所设计的测试系统RBTS-4来验证。该系统共设计35/11 kV变电站3座、11 kV供电母线3条以及连接在SP2的33 kV母线处的备用电源,如图3所示。利用该算例验证,计及检修和备用电源时,结合湖北省咸丰县国家电网公司公共数据库相关数据,所得结果如表1所示。
在表2、图4至图6中:
方式3與方式4相比较:主馈线有隔离开关,电源点与隔离开关的负荷恢复供电时间只有开关操作时间;因此,系统的SAIDI指标从24.711 31 h·户-1·a-1减少到11.866 45 h·户-1·a-1,减小了12.844 86 h·户-1·a-1。
方式5和方式6相比较:主馈线装有分支保护,减少了元件故障对负荷点的影响,使系统的ASAI指标从99.956 1%提高到99.963 9%,提高了0.007 8个百分点。
方式1和方式2相比较:主馈线有分支保护,且增加备用变压器,系统SAIDI指标从4.446 39 h·户-1·a-1减小到2.625 95 h·户-1·a-1,减小了1.820 44 h·户-1·a-1,ASAI指标从99.946 2%提高到99.992 8%,提高了0.046 6个百分点。
4 结束语
本文提出了一种基于最小割集的配电网可靠性评估方法,采用搜索树寻找负荷点的最小连集,然后通过逻辑运算求得负荷点的最小割集,同时考虑了备用电源、计划检修的影响,通过对RBTS-4测试系统的计算、分析和比较,隔离开关前负荷点的可靠性会随着隔离开关的增加而提高到99.963 9%;增加备用电源后,虽不能降低故障率,但能减小负荷点的恢复供电时间,线路后端的可靠性能够增加0.046 6个百分点。这验证了最小割集法的正确合理性,有利于提高电网的供电可靠性。
[参考文献]
[1] 李蕊,李跃,郭威,等.分布式电源接入对配电网可靠性影响的仿真分析[J].电网技术,2016,40(7):2016-2021.
[2] 朱晓荣,王羽凝,金绘民,等.基于马尔科夫链蒙特卡洛方法的光伏电站可靠性评估[J].高电压技术,2017,43(3):1034-1042.
[3] 唐巍,闫涛,王越,等.基于停电序列多状态模型的含微网配电系统可靠性评估[J].电网技术,2019,43(1):285-293.
[4] JOOSHAKI M,ABBASPOUR A,FOTUHI-FIRUZABAD M,et al.Linear Formulations for Topology-Variable-Based Distribution System ReliabilityAssessment Consid-ering Switching Interruptions[J].IEEE Transact-ions on Smart Grid,2020,11(5):4032-4043.
[5] 徐敬友,丁坚勇,杨东俊,等.基于图论及网络等值的配电网可靠性评估方法[J].电气工程学报,2021,16(3):92-98.
[6] 郑渠岸,李超群,张丹丹.基于最小割集的供电可靠性分布式计算研究[J].机电信息,2019(9):7-8.
[7] 潘翀,袁霞,唐伦.大型城市高压配电网可靠性分析[J].电力系统保护与控制,2017,45(3):131-138.
[8] 配电网规划设计技术导则:DL/T 5729—2016[S].
[9] 王波.基于直流配电网设备拓扑分析的可靠性评价方法研究[D].保定:华北电力大学,2019.
[10] 王秀丽,罗沙,谢绍宇,等.基于最小割集的含环网配电系统可靠性评估[J].电力系统保护与控制,2011,39(9):52-58.
[11] ALLAN R N,BILLINTON R,SJARIEF I,et al.A Reliability Test System for Educational Purposes-Basic Distribution Data and Results[J].IEEE Transactions on Power System,1991,6(2):813-820.
[12] IEEE Recommended Practice for the Design of Reliable Industrial and Commercial Power Systems:IEEE Std 493TM-2007(Revision of IEEE Std 493-1997)[S].
收稿日期:2023-05-12
作者简介:卢迪迪(1997—),男,江苏徐州人,硕士,研究方向:电力电子与电气传动。
通信作者:陈俊轶(1992—),女,湖北恩施人,博士,讲师,研究方向:电气信息检测技术。
