高速离心泵叶轮试验模态分析及优化
2023-09-07王彦伟任岩丛李育房
王彦伟,任岩丛,李育房
(武汉工程大学 化工装备强化与本质安全湖北省重点实验室,武汉 430205)
0 引 言
【研究意义】高速离心泵的转速一般大于3 600 r/min,与普通离心泵相比具有扬程高、体积小、质量轻、结构紧凑等一系列优点,在农业灌溉、工业生产等领域被广泛地使用[1]。叶轮作为离心泵中唯一运动的部件,经常在较高的转速下进行工作,会受到各种预应力的作用,从而发生剧烈振动引起共振,使叶轮发生疲劳断裂[2]。为了提高离心泵叶轮结构的可靠性,设计中首先会对叶轮进行模态分析,通过分析叶轮结构的模态特性获得固有频率,对于预防结构破坏、优化结构具有指导性意义[3]。
【研究进展】国内外许多学者[4-6]对离心泵叶轮模态分析做了很多研究,对离心泵叶轮的设计,预防叶片因共振产生疲劳断裂具有指导性意义。Paramasivam等[7]为了降低离心式叶轮中的噪声,设计了导向叶片,取代最初用于所选离心风机的扩散叶片。用这种方式间接增大了叶轮的固有频率,降低了噪声。Sun等[8]采用流固耦合的方法得到流体泵在水中的固有频率,分析了各阶模式的分布情况,发现在水体中由于振动会引起叶轮固有频率降低。陈涛等[9]通过ANSYS仿真与LMS实验分析对比了压气机叶轮在自由、固定和原装3 种方式的固有频率不同,发现叶轮固定式支撑时固有频率最高,为叶轮逆向造型提供了依据。李吉等[10]为避免风机叶轮共振的发生,给叶轮添加预应力状态,并与叶轮处于自由状态下的固有频率进行对比,结果表明,预应力作用下叶轮更能准确反应风机叶轮实际工况。叶福民等[11]利用有限元软件对不同材料离心风机的转子固有频率和振型进行对比分析,结果表明,采用混合材料的离心风机转子与单一材料的离心风机转子相比性能更好,不会发生共振。杨晋萍等[12]将叶轮对称布置和非对称布置的各阶固有频率进行对比分析,结果表明,二者之间的固有频率相差无几,但是叶轮采用对称布置,会使离心泵工作更加稳定,在实际应用中具有一定的指导意义。王学谦等[13]将有限元仿真模态和试验模态分析有机的结合起,对叶轮自由状态下的前六阶固有频率和振型进行对比分析,结果表明二者之间的固有频率相对误差在10%以内。周岭等[14]增强多级离心泵叶轮和壳体进出口处以及出口端盖处刚度,有效避免共振;Huang等[15]为研究涡轮泵转子共振情况,提出涡轮泵叶片模型简化的方法,并将改进前后的转子叶片分别进行模态试验,有效避免共振。Oza等[16]将离心泵叶轮在仿真软件计算出的模态结果与试验测试得到的模态结果进行对比分析,从而验证有限元模型的正确性。Mohammadzadeh等[17]将离心泵转子模型离散化为适量梁单元模型,通过拉格朗日法和有限元法获得的运动全阶方程,用各种液压设计因素对转子进行综合模态分析避免共振。Zeng等[18]在离心泵叶轮上采用非定常CFD、模态分析和谐波响应分析组成的共振风险评估方法,仿真结果与试验结果的对比进行验证,误差在11%以内。证明了共振风险评估方法在实际工程中具有判断共振工作点和破坏性的潜力。
【切入点】总体来看,国内外学者对离心泵模态特性有很多研究工作,但对叶轮的动态性能优化方面研究较少。很多学者仅仅将叶轮由仿真软件计算出的模态结果与试验测试得到的模态结果进行分析,对叶轮结构参数优化很少。【拟解决的关键问题】本文选择叶轮前盖板曲率半径和后盖板曲率半径2 个参数[19]作为影响叶轮振动特性的敏感参数进行优化。选择这2 个参数的原因在于:这2 个参数不仅对叶轮重量影响较小,而且改变这2 个参数对泵的水力性能(流量、扬程)影响也不大。但从叶轮结构而言,这2 个参数的改变可以改变叶轮的刚度,从而影响叶轮的振动频率等动态特性。
1 理论基础
本文求解叶轮处于自由状态下的固有频率和振型,不考虑阻尼的影响。因此该运动方程为[14]:
式中:[M]、{Ü}、[K]和[U]分别为结构质量矩阵、节点加速度矢量、结构刚度矩阵和节点位移矢量。假设上式中的解为简谐函数,表示为:
式中:{φ}为第i(i=1,2,3,…,n)阶模态振型对应的特征向量;ωi为简谐运动角频率(d/s);t为时间(s)。
此特征方程包含一系列相似的关于特征向量的方程,由于在自由振动状态下的系统各节点振幅不可能全部为0,所以上式中的系数行列式等于0,即:
其中ωi2=λi,对每一个特征值λi都有一个特征向量{φ}i使得行列式(4)成立。通过式fi=ωi/2π 即可求得结构的各阶固有频率fi;特征向量{φ}i即可表示第i阶振型。
ANSYS 软件中关于模态提取的方法提供了很多,其中兰佐斯法(Lanczos)法在实际工程中应用最为广泛。其常用于壳体单元模型,能够提取多阶模态,范围较为广泛。
2 离心泵叶轮模态分析
2.1 离心泵模型参数
本文选取Q25H52型高速离心泵中的叶轮进行研究,Q25H52 型高速离心泵和叶轮如图1 所示。

图1 Q25H52 型高速离心泵和叶轮Fig.1 Q25H52 type high speed centrifugal pump and impeller
Q25H52 型高速离心泵设计参数如下:设计流量Q=25m3/h;转速n=6 600 r/min;介质密度ρ=1 200 kg/m3;设计扬程H=52 m。叶轮设计主要参数如下:叶片数Z=6,叶轮外径D2=100 mm,叶轮前盖板曲率半径rq=10 mm,叶轮后盖板曲率半径rh=20 mm。运用Pro/E 软件对离心泵叶轮进行三维实体建模,其叶轮材质性能参数如表1 所示。

表1 叶轮材质性能参数Table 1 Impeller material performance parameters
2.2 叶轮计算模型及网格无关性检验
利用Workbench 软件对离心泵叶轮进行网格划分,划分模式采取四面体网格方式,因为网格划分及其后续求解会占用计算的大量资源,所以网格单元大小采取4 种方案,即0.5、1、2、3 mm,划分后每种方案对应的网格节点和单元数目如表2 所示。
分别对4 种方案进行叶轮前6 阶自由模态求解,得出对应每阶固有频率,对每种方案得出的固有频率进行单位化计算,叶轮前6 阶频率除以最终收敛频率得出单位化的固有频率。从图2 可看出,在节点数目达到200 000 以上时,折线逐渐收敛到1,这说明叶轮固有频率受网格节点密度的影响越来越小,故本文考虑计算结果的准确性及其计算资源状况选取方案2为最终方案,叶轮网格单元尺寸为1 mm,单元数目为121 587,节点数目为210 272,图3为叶轮网格模型。
其实,平平淡淡、实实在在去做人做事,不求“轰轰烈烈”,俏也不争春,努力去做一个对国家、对社会、对他人有益的人,是人生最大的功课。我们有些人现在缺的正是这门功课。
2.3 叶轮自由模态计算结果分析
本文求解叶轮的自由模态,即无约束,无载荷。在计算求解后,会发现叶轮前6 阶固有频率几乎为0,这是由于叶轮在自由模态下处于刚体模态,因此其结构动态特性稳定,只会整体移动或者转动,实际上第1 阶固有频率为第7 阶固有频率。故本文计算离心泵前6 阶固有频率(图4),需要在求解前设置求解的最大阶次为12。

图4 自由状态下叶轮前6 阶振型Fig.4 Impeller front 6th order formation in the free state
从图4 可知,叶轮第1、第2 阶振型相同,其振动方向相互垂直,最大变形发生在进口处和出口处,第5、第6 阶振型相同,其振动方向为二侧摆动,最大变形发生在叶轮轴连接处和出口处,第3 阶振型为叶轮沿轴向上下振动,变形量由叶轮中心沿着半径方向越来越大,在出口处达到最大,第4 阶振型为叶轮出口处沿轮毂处扭转振动,其方向相互垂直,最大变形发生在叶轮出口处。
2.4 叶轮模态试验
2.4.1 试验模态分析原理
本文被测结构为小型叶轮,故选用锤击激励法测试。进行锤击试验时,首先用PCB 力锤锤击叶轮,安装在叶轮上的力传感器和加速度传感器会产生信号,传输至集成振动测试系统内处理,得到传递函数,通过数据传输至LMS Test Lab 软件进行模态的分析以及处理,最后通过曲线拟合得到频谱图以及被测结构的模态参数。原理图如图5 所示。
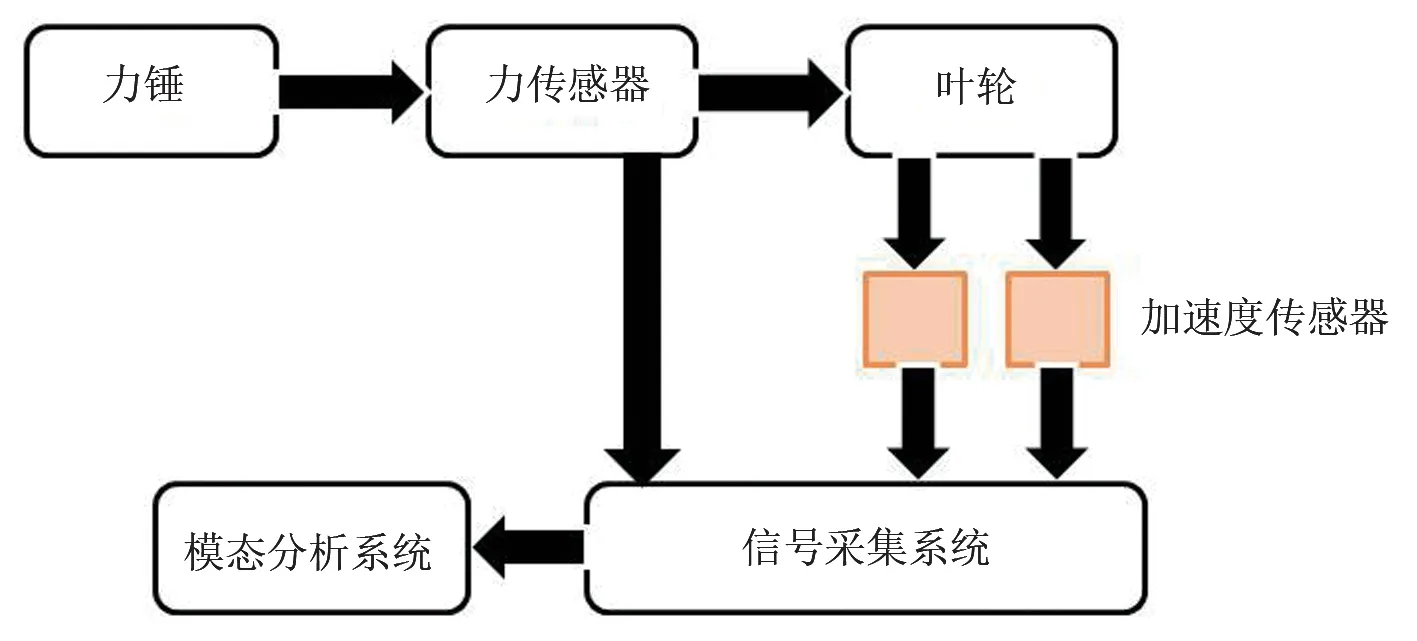
图5 试验模态分析原理Fig.5 Experimental modal analysis schematic
2.4.2 试验仪器设备
本次试验软件部分采用比利时LMS Test Lab 模态分析软件,该软件用于解决振动噪声试验,将多通道数据采集与试验、分析结合起来,其组成部分如图6 所示,分别为集成振动测试系统设备、PCB力锤和PCB 三向传感器。

图6 试验设备Fig.6 Diagram of experimental equipment
2.4.3 试验过程及结果
试验时为了保证叶轮处于自由状态,即无约束、无载荷状态,采用软绳将叶轮悬挂于支架上,如图7(a)所示,选用软绳的目的是因为其刚度远小于叶轮刚度,避免对测试产生干扰,使测出来的固有频率差别较大。固定好叶轮位置,将PCB 三向传感器通过胶水粘到叶轮响应测试点上,该测点应能充分反映试件整体结构振动特性,因此该测试点选择在叶轮前盖板中心位置,如图7(b)所示。锤击测试点的位置直接影响叶轮的固有频率,本次试验中锤击点在叶轮的前盖板、叶片和后盖板3 部分进行布置,如图7(b)、图7(c)所示。其中把前盖板平均分为2 圈,每一圈布置6 个点;由于受到叶片结构的限制,叶片的进口和中部位置即使布点也无法敲击到,因而仅在每个叶片出口位置布置1 个点;叶轮后盖板上在各叶片出口对应垂直位置上分别布置1 个点,这样可以更准确测量叶轮固有频率。若选择别的位置,会导致结果测量变小或不好进行锤击。用记号笔标定这些锤击点,在锤击过程中,锤击的作用力要始终垂直于被测点的表面,如果偏离该方向会使测量值变小。且锤击力度不可太大,要保证锤击后叶轮不会发生剧烈震动,力度过大会超出力传感器感应范围,会使测量值偏大,该力传感器灵敏度为10 mv/g;力度过小传感器测量数值减小导致测量值变小。为了提高锤击结果的准确性,采用对每个测试点连续锤击五次方法,而后对五次的锤击结果做线性平均处理,得到最佳锤击结果,提高信噪比。

图7 叶轮悬挂方式及测试点位置Fig.7 Impeller suspension method and test point position
本文锤击叶轮结束后,为准确得到模态参数,采取Ploy Max 法[20]对得到的频响函数信号进行数据处理,结果如图8 所示。为更加直观地看出叶轮各阶模态的固有频率数值[13],将其中频响函数信号最为清晰的一条单独提取出来与有限元仿真结果进行对比,具体频率响应函数曲线如图9 所示。由图9 可知,叶轮固有频率分别为5 489.3、8 016.5、9 157.2、10 024.6 Hz。

图8 Poly Max 法频响函数结果稳态图Fig.8 Poly Max normal frequency response function result steady-state plot

图9 具体叶轮频率响应函数结果曲线图Fig.9 The result curve of the specific impeller frequency response function
2.5 计算模态与试验模态比较分析
如表3 所示为叶轮的前6 阶计算模态与试验模态比较结果。由于在模态试验时使用的叶轮存在加工误差以及试验中人为每次锤击叶轮的作用力大小、方向以及位置都会对试验结果产生一定误差,因此计算固有频率和试验固有频率之间会存在一定的误差。最后通过反复多次试验,试验各阶固有频率保持相对稳定,其中最大误差处位于第4 阶固有频率,误差值达到了5.12%,但其余阶次固有频率误差都在2%以下,由此可说明本文所建立的叶轮模型比较准确,计算模态仿真模拟结果是可靠的。
3 优化设计分析
本文提出了叶轮的2 种优化方式,即增大叶轮前、后盖板曲率半径,从而改变叶轮的固有频率,使其错开作用在叶轮上的工作频率,防止产生共振引起叶轮疲劳断裂。2 个参数在叶轮中的具体位置如图10 所示。
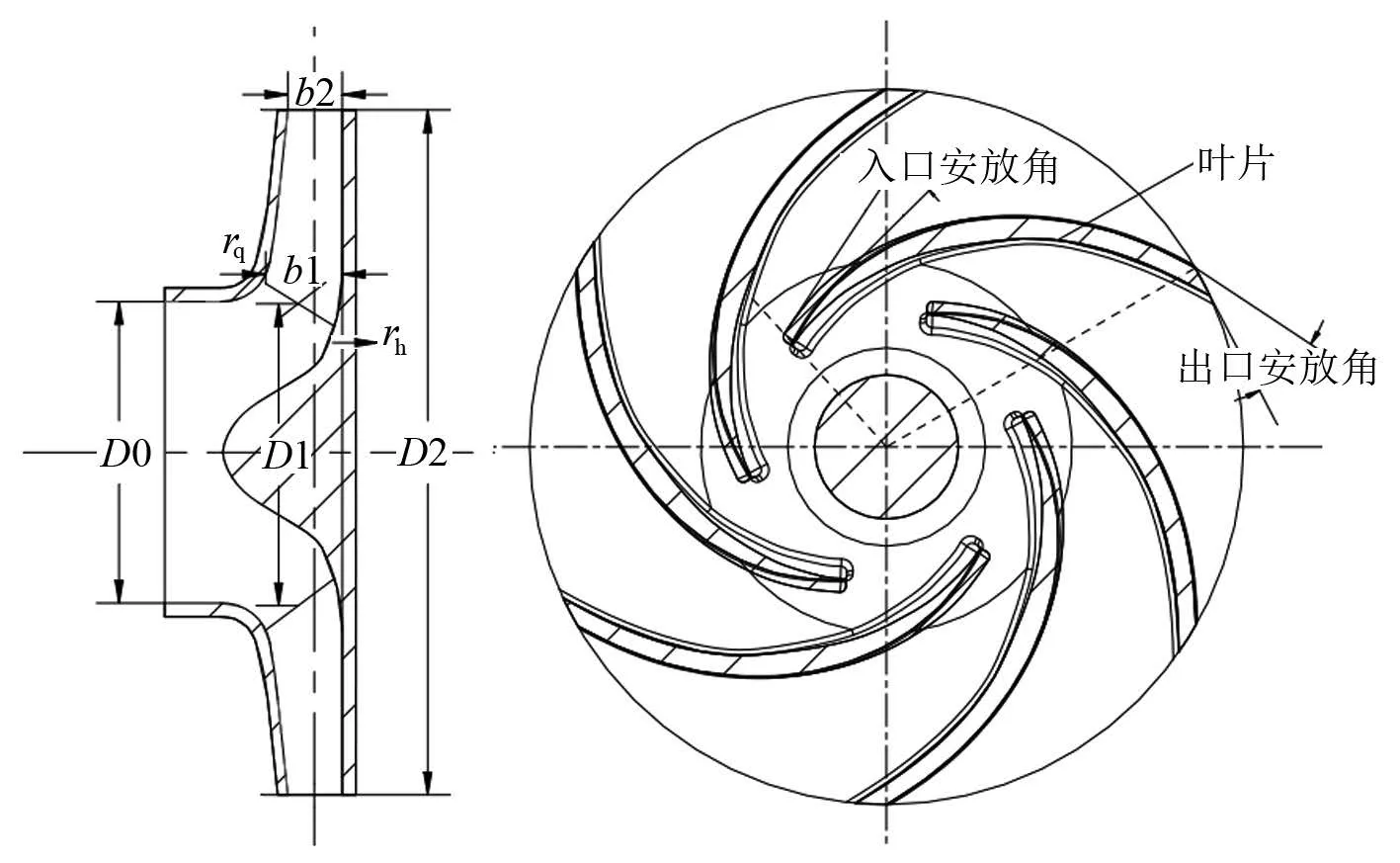
图10 叶轮前盖板曲率半径rq 和后盖板曲率半径rhFig.10 The front cover curvature radius rq and the rear cover curvature radius rh
3.1 改变前盖板曲率半径对叶轮振动特性的影响
对于前盖板曲率半径,在其他参数不变的条件下,将前盖板曲率半径设置为10、12 mm 和14 mm。将模型导入ANSYS Workbench 中进行模态分析。图11 是3 种不同前盖板曲率半径叶轮的模态频率对比图。由图11 可知,增大前盖板曲率半径,可以引起叶轮各阶次固有频率的上升。前盖板曲率半径由10 mm 增大到12 mm 时,各阶次固有频率涨幅不大;当前盖板曲率半径由10 mm 增大到14 mm 时,各阶次固有频率涨幅大幅增大,最大处为第4 阶固有频率,增大10%。如图10 所示,从叶轮结构的角度来讲,前盖板曲率半径前端与叶轮进口直径相连,后端与一条斜边相连,增大前盖板曲率半径,会提高前盖板支撑性,提高叶轮刚性,由式(4)可得,[K]增大,ωi会增大,从而引起频率的增大。因此要想提高叶轮刚度,增大固有频率,可以适当增大叶轮的前盖板曲率半径。

图11 不同前盖板曲率半径叶轮的模态频率Fig.11 Modal frequency of impellers with different curvature radii of the front cover
3.2 改变后盖板曲率半径对叶振动特性的影响
对于后盖板曲率半径,在其他参数不变的条件下,将后盖板曲率半径设置为20、25 mm 和30 mm。将模型导入ANSYS Workbench 中进行模态分析对比。图12是3 种不同后盖板曲率半径叶轮的模态频率对比图。

图12 不同后盖板曲率半径叶轮的模态频率Fig.12 Modal frequency of impellers with different curvature radii of the back cover
由图12 可知,增大后盖板曲率半径,叶轮各阶次固有频率基本保持不变。说明增大后盖板曲率半径对叶轮固有频率影响不大,但是增大后盖板曲率半径经常用在叶轮加工中。由图10 可以看出,与后盖板相连接的是一个直边,继续增大半径,整体结构变化不大,对其刚性影响不是很大,因此频率变化不大。一般情况下,叶轮的后盖板曲率半径越大,铸造更加容易。因此为了提高叶轮的加工工艺性,可以适当地加大叶轮的后盖板曲率半径,但是对于叶轮固有频率影响不大。
4 讨 论
高速离心泵应用于高速场合,会受到外界激振源影响,结构容易产生共振。为提高叶轮固有频率,防止共振,国内外学者做了很多研究。有学者[13,16]对自由状态下的叶轮进行有限元仿真模态和试验模态分析,验证了数值模拟的准确性,但未对叶轮结构参数进行优化分析。石勇强等[21]通过增加叶片厚度、在叶轮前盖板处加筋和增加叶片数量来提升叶轮模态频率,结果得出,3 种方法均可增大叶轮模态频率,其中在叶轮前盖板处加筋对叶轮模态频率影响最大。袁建宝等[22]对离心压缩机叶轮后盖板6 个重要结构参数进行优化设计,优化之后降低后盖板曲率半径,叶轮质量降低16.1%,最大等效应力降低18.5%,但是叶轮模态频率基本不变。
上述学者研究结果表明,叶轮前盖板加筋、叶片数量及叶片厚度参数对其模态频率有较大影响,其本质是通过提高叶轮刚度从而提高模态频率。但这些方法在实际应用中不易加工,成本较高。本文选择一种简单且成本较低的方法,通过增大叶轮前盖板曲率半径,提高前盖板刚度,从而提高叶轮固有频率且更易加工。
对于叶轮后盖板上的结构参数,本文仅研究后盖板曲率半径对叶轮模态频率的影响。经学者研究发现,后盖板其他结构参数对叶轮模态频率的影响较小。但通过优化这些结构参数的方式,可以降低叶轮的质量并减小最大等效应力。
因此,为提高叶轮模态频率,可以适当增大叶轮前盖板的曲率半径,同时适当减小叶轮后盖板的曲率半径,以实现更合理的结构设计。
5 结 论
1)对叶轮进行了仿真自由模态分析与试验模态分析,发现试验模态与仿真计算结果基本一致,证明仿真模拟结果是可靠的。该测试方法可用于离心泵叶轮振动特性研究,可靠性高,为解决旋转机械的共振进行试验测试提供实践参考。
2)根据仿真软件的模态结果分析,在保证其他参数都不变的情况下:增大叶轮前盖板曲率半径,叶轮的前6 阶固有频率皆会升高,当前盖板曲率半径从10 mm 增加到14 mm 时,其中变化最大的为第4 阶固有频率,增加为10%;增大叶轮后盖板曲率半径,叶轮的前6 阶固有频率皆会降低,但是降低的并不明显,当后盖板曲率半径从20 mm 增大到30 mm 时,固有频率仅仅降低0.18%。
3)为更好设计离心泵叶轮,可以选择增大叶轮前盖板曲率半径,从而增加叶轮的固有频率,有效地避免共振。同时,可以将离心泵效率、扬程和模态作为目标,以叶轮前盖板曲率半径、叶片出口角、叶片包角、叶轮进口直径等一系列优化参数建立统一函数关系式,运行求解得出各参数最优值,既提高叶轮的固有频率,又提高叶轮的水力性能。
(作者声明本文无实际或潜在的利益冲突)
