基于樽海鞘群算法的负荷管理错峰计划优化

谭 娟

（国网长沙供电公司客户服务中心，湖南 长沙 410000）

随着我国经济的飞速发展，电力负荷需求量越来越大，在用电高峰期偶尔也会出现“用电荒”等情况，给人们生产生活带来了一定的影响。负荷管理是优化资源配置和解决电力供需平衡的重要手段。错峰用电能够有效降低高峰负荷，是一种行之有效的负荷管理方法。因此，合理安排错峰计划，对降低发电成本和提高能源利用率具有重要意义。

文献[1]通过对不同类型负荷的特点进行研究，采用灰色G（1，1）模型对存在峰谷型负荷进行了预测，根据预测结果实施差异化错峰停电，制定最优错峰负荷管理方案，提高了负荷管理的效率。文献[2]以平衡日的错峰电量为目标函数，建立工业用户的错峰用电模型，对工业用户的轮休、检修时间进行了优化，算例分析结果表明，用户更多的参与错峰计划可以明显增大错峰量，降低用电成本。文献[3]提出了一种最优错峰计划生成方法，以受影响用户数最少为目标函数，建立最优错峰计划生成模型，采用遗传算法对模型进行了求解，获得了错峰运行方式下电网的最优错峰计划。现有研究的负荷管理策略不合理，因此针对负荷管理错峰计划的优化有待进一步研究。

1 樽海鞘群优化算法

2017 年，Mirjalili 等人提出了一种新型启发式优化算法——樽海鞘群算法[4-5]（Salp Swarm Algorithm，SSA），它是根据樽海鞘种群的觅食行为提出来的。樽海鞘是一种与水母非常相似的海洋动物，它们的移动方式和身体组织几乎一致，在觅食过程中，樽海鞘个体首尾之间连接成一种链式进行移动，个体之间相互协作，最终找到食物。

SSA 算法的原理如下：将种群划分为领导者和追随者，领导者的作用是带领追随者寻找食物，令食物为G，樽海鞘群在d维空间中的位置矩阵设为Sn×d，其中元素si，j表示第i个樽海鞘在第j维搜索空间的位置，n表示樽海鞘种群容量。

SSA 算法中的领导者依据食物位置更新自身位置，领导者的位置更新如公式（1）所示。

式中：Gj为领导者的位置；uj为第j维空间的上限值；lj为第j维空间的下限值；r1、r2、r3均为调整系数，；r1、r2∈[0，1]；r1的计算如公式（2）所示。

式中：k为当前迭代次数；kmax为最大迭代次数。

追随者跟随领导者的位置移动，追随者的位置更新如公式（3）所示。

式中：si，j为第i个樽海鞘在第j维搜索空间中的位置；si-1，j为第i-1 个樽海鞘在第j维搜索空间中的位置；2≤i≤n。

与其他优化算法相比，SSA 算法具有以下2 个优点：一是樽海鞘群个体活跃度较高，种群的全局搜索能力较强；二是在追随者位置更新过程中，樽海鞘个体之间协调性较好，不易陷入局部最优。

2 负荷管理错峰计划优化模型

2.1 目标函数

当制定负荷管理策略时，应考虑对用户的影响[6]。该文以负荷管理中错峰计划用户受影响指数最小为目标函数，其数学模型如公式（4）所示。

式中：f为负荷管理中错峰计划用户受影响指标；N为用户总数；Ti为错峰用户i用电行为的变更时间；Wi为错峰用户i单日的用电量；g（Ti）为用户用电行为变更时间的加权系数，变更时间越长，加权系数越大，考虑到用电行为提前对用户造成的影响比推迟更大，因此采用下列加权方法，如公式（5）所示。

2.2 约束条件

2.2.1 支路潮流约束

在电力系统中，受线径、材料等约束，每条支路传输的功率都是有上限的，支路潮流约束是指支路传输功率不得超过其传输极限功率，支路潮流约束的数学表达式如公式（6）所示。

式中：Sj为第j条支路的负荷；Sj，max为第j条支路的负荷最大值。

2.2.2 节点电压约束

节点电压是表征电力系统稳定性和电能质量的重要指标，为了确保负荷管理过程中系统节点波动值在一定范围内，须对节点电压的上下限进行约束，节点电压约束的数学表达式如公式（7）所示。

式中：Ui为节点i的电压幅值；Umin、Umax分别为节点i电压幅值的最小值和最大值。

3 考虑运行方式的错峰计划调整

为进一步减少错峰计划对用户的影响，通过对配电网重构来调整运行方式，即将配电网系统中开关作为节点，变压器和输电线路作为方向指向潮流的有向线段，从而调整系统运行方式。

3.1 联络开关操作

联络开关采用单步平移的方式进行操作[7]，具体操作方法如下：合上联络开关，并向潮流反方向的一个相邻开关断开，并将其作为一个新的联络节点，因此每个联络开关进行单步平移后会出现2 种情况：一是向左平移操作，二是向右平移操作。如果平移后系统中没有孤岛产生，那么系统运行方式保持不变。

3.2 错峰计划调整

通过操作联络开关，即可根据下列步骤调整错峰计划：1）令系统当前运行方式为TP0、用户负荷曲线调整时间为f0，则有fR=f0、TPR= TP0。2）将运行方式TP0下的联络开关全部断开，并放入队列R 中，则有k=0。3）从队列R 取出任意一个联络开关节点，并执行向左平移操作，得到新的运行方式TP1，并得到对应的f1，如果满足f1＜fR，则有fR=f1、TPR= TP1、k=1。然后再执行向右平移操作，得到对应的f2，如果满足f2＜fR，则有fR=f2、TPR= TP2、k=2。4）如果队列R中k≠0，则返回步骤（3），否则执行下一步骤。5）如果k=0，则结束平移操作，此时TPR 为错峰计划对应的运行方式，fR即为用户负荷曲线调整时间，否则返步骤（2）。

3.3 SSA 算法求解错峰计划优化模型

该文采用SSA 算法对错峰计划优化模型进行求解，图1为求解流程图，求解步骤如下。1）设置系统参数及SSA 算法的相关参数，包括樽海鞘群数量和最大迭代次数。2）随机选取M种运行方式放入队列Q中。3）从队列Q中选出一种运行方式作为系统初始运行方式。4）采用SSA 算法对目标函数进行优化，获取当前运行方式下的最优解OP。5）采用单步平移法获取新的运行方式。6）采用SSA 算法获取新的最优解OP1，比较OP1 和OP 的值，如果OP1 更好，则用OP1 替代OP，否则OP 保持不变。7）判断系统所有开关是否满足约束条件，如果满足，那么执行下一步骤，否则返回步骤（5）。8）判断队列Q是否为空，如果为空则输出最优解，获得最优错峰计划，否则返回（3）。

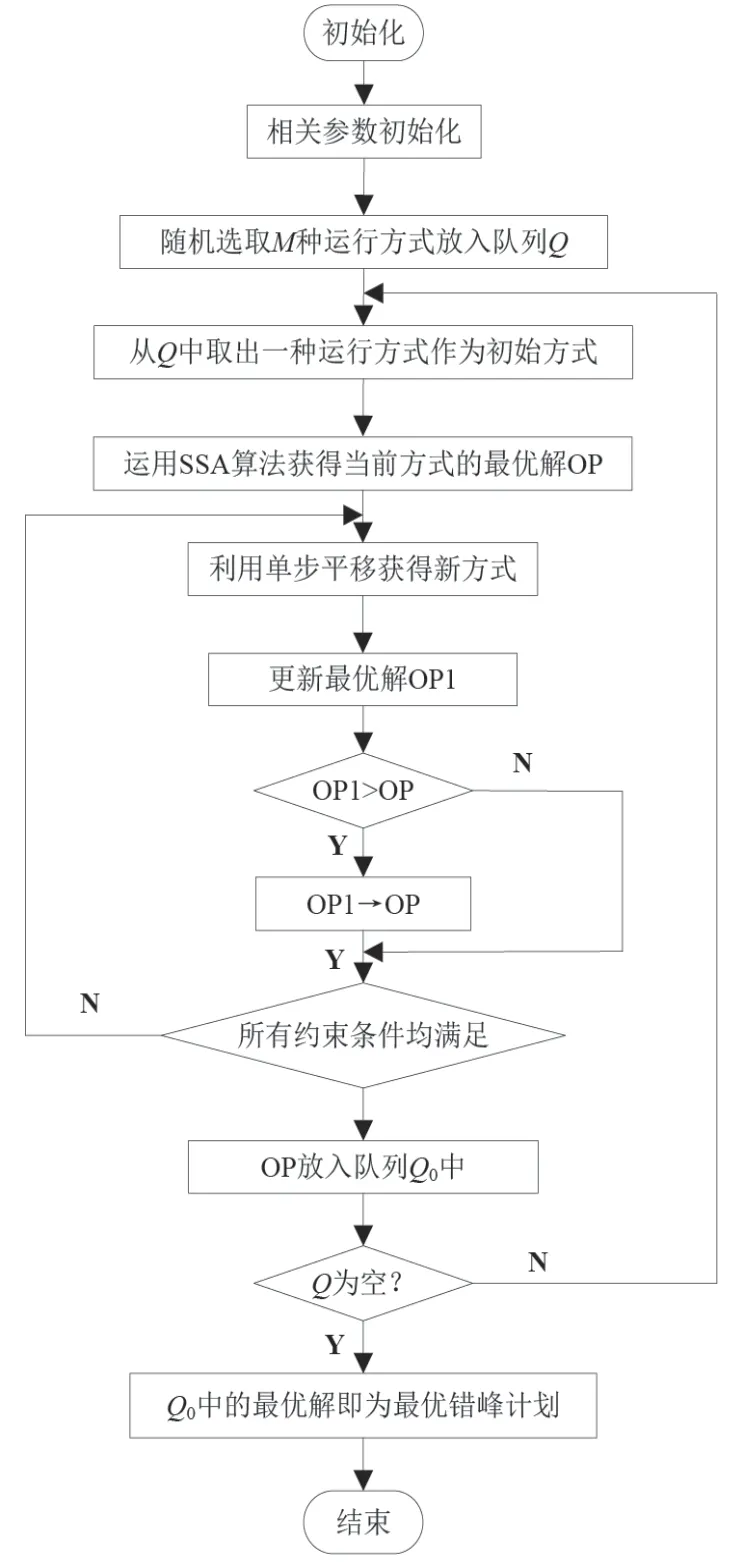
图1 错峰计划优化模型求解流程图

4 算例分析

4.1 系统参数

采用经典三分割配电网络进行仿真分析，系统参数可参考文献[8]，其网络结构如图2 所示。在该系统中，电源节点15 和16 的容量为3.6MW，其余电源节点容量为3.1MW。系统中共有35 个负荷，各负荷属性见表1。

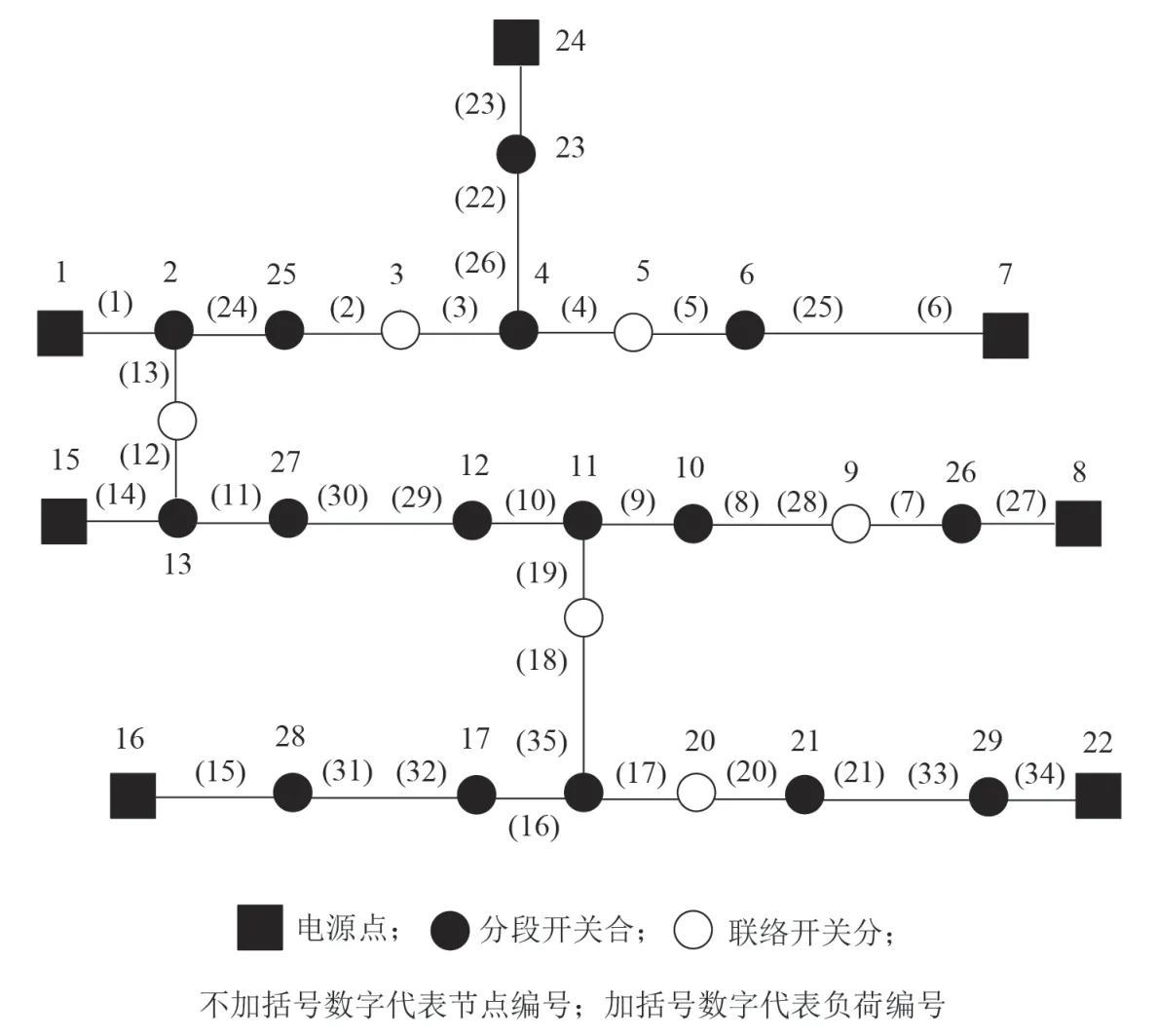
图2 三分割配电网络结构简图

表1 各负荷属性

SSA 算法的参数设置如下[9]：樽海鞘种群n=30、最大迭代次数kmax=300。为了便于计算，假设周一到周五的负荷曲线是一致的，周六和周日的负荷曲线是一致的。

4.2 结果分析

采用下列2 个场景进行对比，以验证负荷管理中错峰计划优化的作用。场景1：采用当前运行方式，只考虑作息时间，不考虑轮休制度。场景2：综合考虑作息时间、运行方式和轮休制度，采用该文所提SSA 算法进行错峰计划优化。

在MATLAB 中对场景1 和场景2 进行仿真分析，2 种场景的仿真结果见表2，场景1 和场景2 的负荷管理策略分别见表3 和表4。

表2 2 种场景的仿真结果

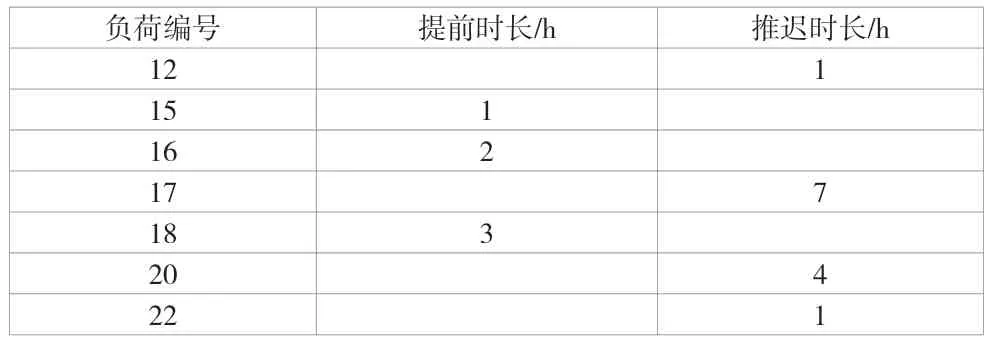
表3 场景1 负荷管理策略

表4 场景2 负荷管理策略

由表2 可知，场景一的错峰计划用户受影响指数最小值为103，场景2 的错峰计划用户受影响指数最小值为59，场景2 在场景1 的基础上降低了42.72%。对比表3 和表4 可知，场景2 中考虑了最优轮休计划后，最优作息时间与场景1 相比更合理。综上所述，在制定负荷管理中的错峰计划的过程中，考虑的因素越多，优化效果越好。

4 结论

该文以负荷管理中错峰计划用户受影响指数最小为目标函数，建立基于樽海鞘群算法的负荷管理错峰计划优化模型，采用经典三分割配电网络进行仿真分析，结果表明，综合考虑作息时间、运行方式和轮休制度时的错峰计划用户受影响指数最小值为59，与只考虑作息时间的最优解相比，降低了42.72%，当制定负荷管理中的错峰计划时，考虑的因素越多，优化效果越好。