小卫星分离姿态干扰及抑制分析

王金昌， 毛鹏程， 吕 涛， 徐 奎， 徐方舟

（中国运载火箭技术研究院，北京 100076）

近年来，商业航天快速发展，小卫星具有重要的价值和作用。以美国太空探索技术公司（SpaceX）为例，该公司将计划在太空部署12 000 颗卫星，提供移动互联网服务。这或将引发未来移动互联网的技术革命［1-2］。受发射成本等因素限制，小卫星一般采用一箭多星发射，根据需要一次发射数量可达几十颗甚至上百颗［3］。

一箭多星任务中，小卫星安装空间受限、布局方式复杂。因此，对小卫星的分离姿态、速度、角速度，以及分离安全性都提出了较高的要求。

小卫星一般采用爆炸螺栓+弹簧的分离方式，受弹簧刚度与预紧力偏差、卫星与航天器质量特性偏差、安装偏差、初始运动参数等因素影响，小卫星的分离干扰存在较大的不确定性。因此，有必要对小卫星的分离干扰采取抑制措施，并对其分离安全性进行分析［4］。

星箭分离动力学建模过程复杂，多进行简化处理，例如在文献［5］中，建立了卫星分离过程的动力学模型，通过模型可直观地获取各干扰因素对卫星分离过程的影响［5］。该模型较为复杂，求解难度大，适用于定性评估各类干扰因素的影响。为了能够求解卫星分离后的运动参数，本研究在此建模思想的基础上进行简化与改进，建立卫星分离过程的六自由度动力学模型，分析了卫星分离过程的速度和角速度，并通过ADAMS建立虚拟样机模型，通过分析结果的一致性来评估所建立的动力学模型的准确性。为评估导向机构对小卫星星箭分离干扰的抑制作用，分析了导向机构作用下的星箭分离过程，进一步比较了导向机构前后的小卫星分离速度、角速度，验证了导向机构对卫星分离偏差的改善作用，同时也对导向机构的参数进行了优化。

1 卫星分离的动力学模型建立与求解

1.1 动力学模型建立

图1 为某一颗搭载星分离过程的简化模型，假设该卫星质量均匀分布，质心位于直角坐标系O-XYZ的原点，其相对质心的转动惯量分别为IX、IY和IZ。该搭载星通过爆炸螺栓实现解锁，通过弹簧力提供分离速度，图1 中A、B、C、D4 个弹簧均匀分布，弹簧顶端为等效轻质小球，与卫星底部贴紧，相邻2 个弹簧之间距离为L，弹簧刚度分别为KA、KB、KC、KD，弹簧预紧力分别为FA0、FB0、FC0、FD0，分离过程中弹簧力大小分别为FA、FB、FC、FD，初始压缩量分别为XA0、XB0、XC0、XD0，4 个支撑点位移分别为XA、XB、XC、XD，X轴为卫星分离方向，卫星质心沿X轴位移为x，绕Y轴转动角度为θY，绕Z轴转动角度为θZ［6-7］。

图1 分离仿真模型Fig.1 Simulation model of separation

为简化模型，进行如下假设：

（1）由于火箭末级与卫星相比质量足够大（超过卫星质量的100 倍），火箭运动时对卫星影响小到可以忽略不计，因此分析时认为火箭位置固定不变；

（2）忽略卫星分离过程中的阻力与摩擦力；

（3）4个弹簧的刚度系数相等。

根据4 个弹簧支点的几何关系，在一定转动角度范围内，4个弹簧支撑点位移等效为

分离过程中弹簧力大小为

在式（2）中，FA、FB、FC、FD的取值范围为非负值，当XA≥XA0、XB≥XB0、XC≥XC0、XD≥XD0时，FA、FB、FC、FD取值均为0。

假设卫星Y轴及Z轴方向没有作用力，X轴方向没有作用力矩，根据牛顿第二定律［8］，有

为简化模型，假设4 个弹簧的刚度系数均为K，由式（1）～（3）可得

1.2 动力学模型求解

上述模型中，设卫星质量m为50 kg，火箭末级质量M为5 750 kg，相邻2个弹簧之间距离L为0.226 m，弹簧刚度系数K为8 750 N/m，转动惯量IX为1.7 kg·m2，IY为1.9 kg·m2，IZ为1.9 kg·m2，弹簧初始压缩量XA0为39 mm，XB0为40 mm，XC0为41 mm，XD0为42 mm。

根据上述公式推导，在MATLAB/Simulink 环境下建立动力学模型并进行求解。需要特别说明的是，在Simulink 环境下，须设置弹簧力的取值范围，模拟弹簧力在卫星分离之后取值为0。

经仿真分析，卫星分离后绕Y轴转动的最大角速度θ′Y为0.0341（°）/s，绕Z轴转动的最大角速度θ′Z为6.117（°）/s，沿X轴方向分离速度x′为1.072 m/s。如图2所示。

图2 卫星分离后的运动参数Fig.2 The motion parameters after satellite separation

在上述分析过程中简化了动力学模型，而实际卫星分离过程受前文所述的多种因素影响，若将这些因素全部考虑进去，建模及求解难度极大。

分析更复杂的、多干扰要素的卫星分离过程需借助虚拟样机等手段，下面采用ADAMS 建立该卫星分离的虚拟样机模型，建模时考虑了多种因素干扰，并分析导向机构对卫星分离偏差的抑制效果。

2 虚拟样机的模型建立

在ADAMS 环境下建立如图3 所示的虚拟样机模型。在运载火箭末级上共搭载8颗小卫星，其中4颗小卫星搭载于主卫星支架内部，其余4颗搭载于运载火箭末级的前锥段。以主卫星支架内部的其中1 颗小卫星为研究对象，对小卫星的分离过程进行分析。其他小卫星的分离仿真可通过编制脚本程序，通过控制小卫星与火箭之间固定副的失效时刻，来实现卫星在确定时刻的分离。本研究所有卫星的参数设置及分析方法相同，其他几颗卫星的仿真过程分析在此不再赘述。

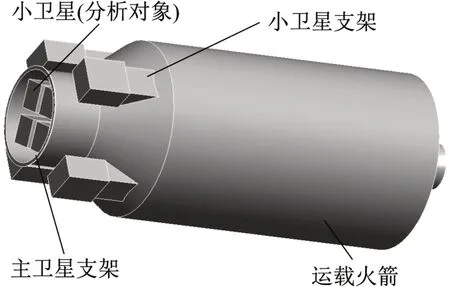
图3 多星分离的虚拟样机模型Fig.3 Virtual prototype of multi-satellite separation system

如图4 所示，作为分析对象的小卫星通过4 组弹簧+爆炸螺栓和运载火箭末级连接，小卫星体表装有导向套，运载火箭末级装有导向杆，导向套与导向杆采用间隙配合，用于消除小卫星分离过程中的姿态干扰。

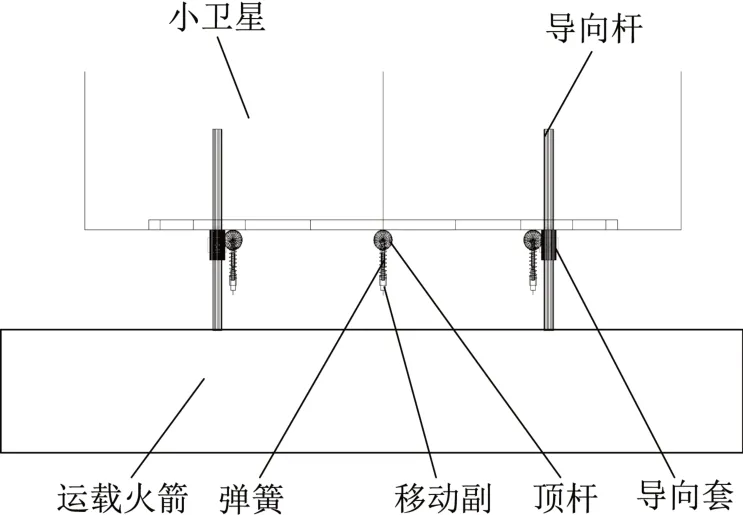
图4 星箭接口定义Fig.4 Interface definition of satellite and launch vehicle

在ADAMS 环境下，导向套与导向杆之间添加CONTACT 接触力约束，通过控制CONTACT 接触力是否失效，可比较有无导向装置小卫星分离姿态的变化。弹簧中的一端与火箭末级连接，另一端连接一轻质小球，模拟弹簧顶杆，小球与卫星底面之间添加CONTACT 接触力，实现了弹簧+爆炸螺栓功能的模拟。小卫星与运载火箭之间添加Fixed固定副，通过脚本控制固定副的失效时刻来实现卫星的分离［9］。

3 卫星分离干扰分析

按照上文动力学模型参数设置虚拟样机模型参数，分析弹簧存在偏差和电分离插头异常分离情况下，对卫星分离姿态的干扰作用。

3.1 弹簧偏差对卫星的分离干扰分析

按照上文Simulink 环境下的弹簧参数对ADAMS模型进行设置，并进行仿真分析。卫星分离后绕X轴转动无角速度，绕Y轴转动的角速度θ′Y为0.0496（°）/s，绕Z轴转动的角速度θ′Z为5.946（°）/s，沿X轴方向的分离速度x′为1.060 m/s。MATLAB/Simulink 环境下的仿真结果与ADAMS环境下的分析结果相比差值分别为-0.016（°）/s，0.171（°）/s和0.012 m/s。见图5

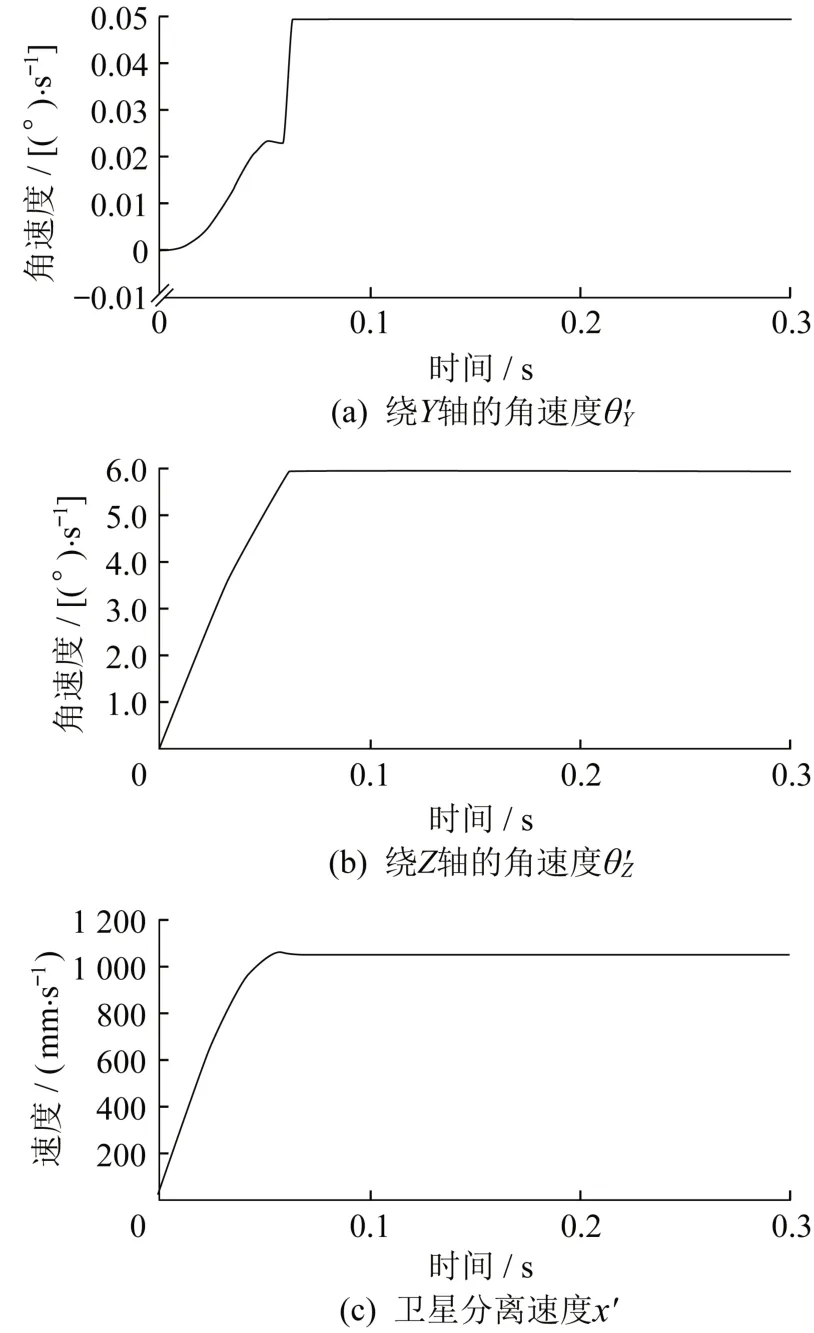
图5 卫星分离后的运动参数Fig.5 The motion parameters after satellite separation

与Simulink环境分析结果相比，在ADAMS环境下还考虑了运载火箭末级质量、卫星在火箭上偏质心安装、接触阻尼与摩擦等因素的影响，所以2 种方法分析结果有小量级差值，尤其是绕Y轴的角速度θ̇Y，由于受各种干扰因素影响在初始分离阶段差异性明显，但整体来看，2种方法分析结果差异值不大，曲线一致性较好。

3.2 电分离插头拉力干扰对卫星的分离干扰分析

为进一步分析电分离插头拉力干扰对卫星的分离干扰，在上一分析模型中加入电分离插头机械分离时产生的拉脱力。

卫星与运载火箭末级一般采用电分离插头实现电气连接，在卫星分离过程中，电分离插头机械分离产生的拉力可能会给小卫星分离姿态带来较大干扰，甚至导致碰撞事故发生［10］。

正常情况下，电分离插头通过电信号实现自动分离。若电分离功能失效，电分离插头则采用钢索拉脱方式实现机械分离。以某一型号电分离插头为例，拉脱力峰值约98 N，卫星分离60 mm 时钢索起作用，拉力作用行程不大于5 mm，拉力方向与过卫星质心轴线距离为150 mm，分析导向装置对分离插头拉力干扰的消除效果。在ADAMS 环境下，分离插头拉力的模拟可通过2 个Step 函数叠加实现［11］，拉力起作用的时刻由钢索长度决定，仿真分析后的电分离插头拉力作用曲线如图6所示，该拉力作用时间约4 ms。

图6 电分离插头作用力Fig.6 The force of the electrical separation plug

如图7 所示，电分离插头机械分离条件下，卫星分离总角速度为4.648（°）/s。而电分离插头正常电分离条件下，卫星分离总角速度为5.946（°）/s，大于电分离插头机械分离条件下的角速度。

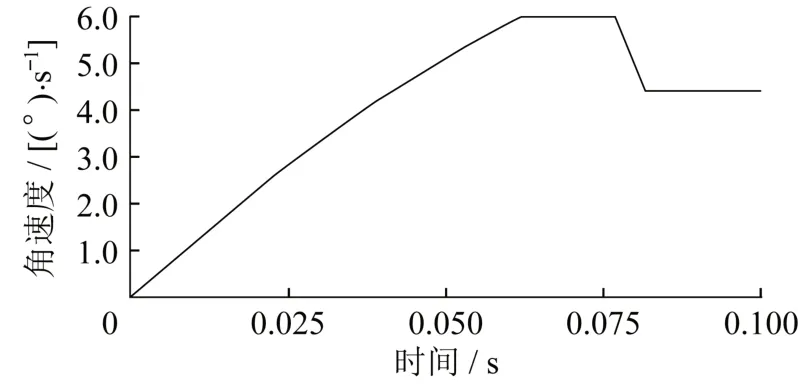
图7 电分离插头机械分离条件下的总角速度Fig.7 The total angular velocity of the satellite with the electrical seperation plug mechanical separated

从卫星分离后的总角速度来看，电分离插头机械分离反而减小了卫星分离后的姿态干扰。出现这种情况的原因是，电分离插头拉力与弹簧偏差形成的干扰相互抵消。在实际应用中，弹簧偏差干扰方向无法准确测量，2 种干扰的合成具有不确定性。因此，任何非确定性干扰都不是人们所期望的。

4 卫星分离干扰的抑制作用分析

4.1 卫星分离干扰的抑制方法

减小卫星分离过程中的各类干扰可提高卫星分离姿态精度，具体方法包括：提高运载器平台的姿态控制精度、提高弹簧制造精度及其安装精度、卫星分离方向尽量靠近运载器平台质心、避免电分离插头拉力干扰、增加导向装置等［12］。

卫星分离过程中的姿态干扰因素不确定性较大，无法精确控制，而通过增加导向装置能够有效抑制分离姿态干扰，同时能够降低卫星分离时产生的碰撞风险。尤其在多星发射任务中，分离干扰因素多，并且卫星布局方式复杂，极易造成碰撞危险，因而增加导向装置尤为重要。

增加导向装置，可以提高卫星分离姿态精度，同时能够降低碰撞危险。但增加导向装置的同时，也增加了结构重量，还带来潜在的卡滞风险。因此，需要对导向装置的材料、长度进行分析。

4.2 导向装置的参数设计及抑制干扰能力分析

卫星姿态干扰抑制一般通过增加导向装置来实现，导向装置材料和导向距离对卫星分离姿态干扰抑制有重要的影响。为了分析导向装置参数对卫星分离姿态干扰的抑制作用，可选用不同材料的导向套和不同长度的导向杆进行模拟。导向杆与导向套材料的接触力参数设置如表1所示，具体分析工况如表2所示。

表1 不同材料的接触力参数Tab.1 The contact force parameters for different materials

表2 不同材料及导向装置长度下的分离总角速度Tab.2 The separation angular velocity for different materials and guide lengths

按照表2 所列的14 个工况进行分析，分析结果曲线如图8-9所示，卫星分离后的总角速度如表2所示。

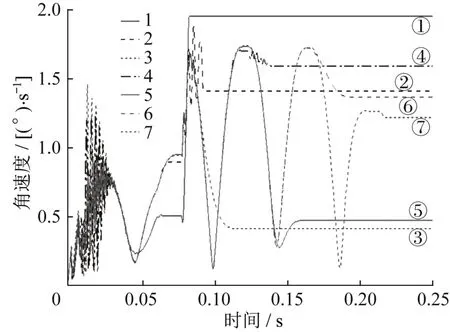
图8 采用金属导向套时不同导向距离的分离角速度Fig.8 The separation angular velocity in different length guiding mechanism with metal guiding ring

从分析结果可得出如下结论。

（1）导向距离越长，对卫星分离后的姿态干扰抑制作用越大；但同时导向距离越长，分离系统质量越大，导向杆随着长度增加而刚度减小，从而增加分离过程中导向装置卡滞的风险。金属导向套在导向装置作用期间，卫星角速度呈现出周期振荡趋势，并且振幅衰减不明显，在0.1 s 后导向装置作用已经不明显，对于金属导向套来说，导向距离100 mm即可满足要求。

（2）如表2 所示，卫星分离后的角速度并非随导向距离的增加而减小，而是具有一定的不确定性。主要原因是，由于在导向期间卫星的角速度呈振荡衰减趋势，导向装置在不同时刻失去作用，导致分离角速度的不确定性。

（3）卫星分离后的角速度不能够彻底消除，一方面由于卫星在火箭末级上偏质心安装，与卫星和运载火箭相互作用产生相对角速度有关；另一方面，导向装置相互作用过程中，不能够完全吸收干扰能量。即使如此，设置导向装置后的卫星分离角速度已经得到极大改善，本研究所分析的14 个工况中，采用导向装置，卫星分离后的角速度减小了58%～91.1%。

（4）如图9 所示，采用金属导向套0.1 s 时卫星角速度降到0.15（°）/s，而采用非金属导向套0.2 s 时卫星角速度降到0.813（°）/s。可见，采用非金属材料的导向套，由于接触刚度较小，卫星姿态干扰消除较慢，需要较长的导向距离，增加了分离过程中的卡滞风险。因此，提高导向杆与导向套的接触刚度能够快速消除干扰，减小导向杆的长度。

图9 采用非金属导向套时不同导向距离的分离角速度Fig.9 The separation angular velocity in different length guiding mechanism with nonmetal guiding ring

5 结 论

本研究建立了一箭多星分离过程的动力学模型，通过MATLAB/Simulink实现卫星空间六自由度的分离过程仿真。该模型只适用于分离弹簧存在偏差、卫星质量远小于火箭末级质量情况下的卫星分离过程仿真。若考虑卫星分离过程的全部干扰因素并评估干扰抑制效果，须借助虚拟样机手段进行仿真分析。本研究借助ADAMS虚拟样机软件，对卫星分离过程的干扰及干扰抑制效果进行仿真分析，该分析方法适用于所有卫星分离过程的仿真分析，通过分析得出如下结论。

（1）MATLAB/Simulink 环境下的仿真结果与ADAMS 环境下的分析结果相比，θ′Y、θ′Z、x′之差分别为-0.016（°）/s，0.171（°）/s和0.012 m/s，一致性较好。采用建立数学模型、MATLAB求解的方法适合计算简单的卫星分离问题，包括分离弹簧参数设计、分离速度计算、分离角速度预估等分析。对于复杂卫星分离过程，业界通常采用ADAMS等虚拟样机手段。

（2）弹簧安装偏差、电分离插头拉力、火箭姿态干扰是卫星分离过程的主要干扰因素，以本研究设置的干扰参数为例，多种因素共同作用可引起1.298（°）/s的角速度偏差，通过增加导向装置可使角速度减小91.1%，有效抑制分离干扰。

（3）导向杆与导向材料应选择接触刚度较大的材料，刚度增大有利于快速降低干扰，本研究采用接触刚度较大的金属导向套0.1 s 时卫星角速度降到0.150（°）/s，而采用接触刚度较小的非金属导向套0.2 s卫星角速度才降到0.813（°）/s。

（4）导向杆的刚度随着长度增加而减小，增加导向杆长度也增加了分离卡滞风险，同时也增加了系统重量。在有效降低干扰前提下，导向距离越短越好。最优导向距离可通过仿真求解，以本研究中的金属导向套为例，导向距离100 mm为最优导向距离。

（5）受火箭末级姿态干扰及卫星安装质心偏差等因素影响，即使设置导向装置也无法将姿态干扰消除，但至少能够有效降低卫星相对于火箭末级的相对角速度，从避免碰撞和安全分离角度来说具有一定的必要性。