曲线刚构桥八边形异厚度变截面中空桥墩的承载特性

吴军 李有兵 孙建阳 崔溦 刘贵锋

(1.中国电建市政建设集团有限公司，天津 300384；2.天津大学水利工程仿真与安全国家重点实验室，天津 300350)

关键字：八边形异厚度空心桥墩；曲线连续刚构桥；塑性损伤；线性失稳；极限承载力

0 引言

桥墩是支承桥跨结构并将恒载和车辆活载传至地基的重要结构物，由于施工和运行期荷载条件差异较大，其承载性能对于桥梁安全具有重要影响。常见的桥墩截面有圆形、圆端形、矩形及相应空心截面。许多学者针对不同截面形状的桥墩在各种荷载作用下的受力特性及承载能力开展了物理实验和数值模拟。文献[1-3]通过拟静力实验和数值模拟方法，指出圆端形截面的桥墩展现出较好的延性性能、适合在地震严重区域采用。韦旺[4]基于多种薄壁空心墩的拟静力试验提出了空心桥墩的抗震性能及延性指标的等级和范围，评估l端空心墩桥梁和矩形空心墩桥梁实际工程的抗震性能。Rashid和Abdul[5]通过模拟6种不同的桥墩形状，分析桥墩形状对局部冲刷的影响，指出八边形桥墩减少冲刷深度的效果最好，其次是圆端形桥墩。

与圆形空心截面和圆端形截面相比，八边形变截面空心桥墩在桥墩模板安装和施工方面简单，容易操作。但国内桥墩截面采用该类型桥墩的案例很少，有必要深入研究其承载性能。本文依托国外一曲线形连续刚构桥工程，采用混凝土塑性损伤模型，对八边形异厚度变截面空心桥墩最大悬臂工况和极限承载工况开展有限元模拟，分析该类截面与八边形等厚变截面空心桥墩和矩形变截面空心桥墩受力特性的区别，并明晰其变形及破坏模式。

1 混凝土的塑性损伤模型

混凝土塑性损伤（CDP）模型[6]基于塑性理论，采用各向同性弹性损伤与各向同性拉伸和压缩塑性理论来体现混凝土的非弹性行为。因此采用CDP模型模拟桥墩在集中力和弯矩共同作用下的极限破坏模式和力学特性。

以计算拉伸损伤为例，由不同标号混凝土的弹性模量及抗拉强度求得弹性应变。然后由规范公式求得非弹性阶段的应力-应变关系[7]：

式中：εt,r是峰值拉应变，可由相应单轴抗拉强度代表值查规范取得；是单轴抗拉强度代表值；αt是单轴受拉应力-应变曲线下降段的形式参数，反映混凝土下降段的发展趋势，查规范可得。

2 数值模型

2.1 工程概况

欧洲某大桥是“一带一路”上的重要交通连接点，为一座七跨曲线连续刚构桥，上部主梁为双向预应力混凝土结构，箱型截面，长945m，宽21.92m，如图1所示。桥面纵向坡度为0.68%，横向坡度为5.5%。桥梁设置桥台两个，桥墩6个。桥墩为变截面八边形空心截面，包括横向直线段、纵向直线段和连接斜段。横向直线段的长度尺寸从墩底至墩顶方向渐变小设置，纵向直线段从墩底至墩顶方向“先减后增”设置，连接斜段从墩底至墩顶方向定值设置；靠近刚构桥弯曲内侧的内侧纵向直线段厚度为80cm，外侧纵向直线段厚度为60cm；在竖向采用双向放坡设计，截面尺寸从墩底往墩顶由大变小再变大。

图1 桥梁总体布置图

2.2 有限元模型

依据惯性矩等效原则，将S3桥墩沿高度两端大、中间小的八边形空心截面换算成等效惯性矩的矩形空心截面。建立桥墩异厚模型（内侧80cm，外侧60cm）和等厚模型（内外侧70cm），模型体积相差0.5%以下，对桥墩底部施加固结约束，顶部自由。

2.3 计算荷载

计算荷载考虑桥梁自重，重力加速度为9.8kg/s2。区别于直线型桥梁，曲线刚构桥的上部主梁结构重心偏向曲线内侧，对桥墩产生偏心弯矩。为便于对比不同桥墩的结构特性，首先利用主梁和桥墩一体的数值结果，将上部主梁最大悬臂部分的重量等效成集中力F=72635kN和偏心弯矩M=58108kN·m，并施加在桥墩顶部参考点上。

2.4 材料参数

在ABAQUS中需要输入的C50混凝土应力应变曲线主要参数如表1所示。根据经验得出C50混凝土塑性损伤模型的其他参数，如表2所示。桥墩混凝土的基本力学参数如表3所示。

表1 C50混凝土塑性损伤模型主要参数

表2 C50及C60混凝土塑性损伤模型其他参数

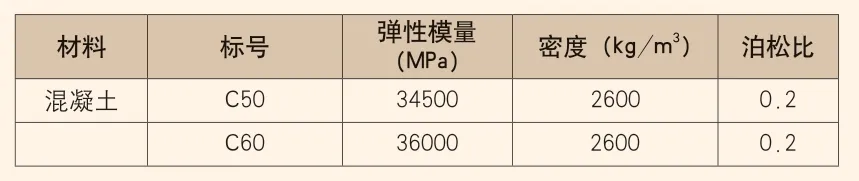
表3 材料的其他力学参数

3 结果与分析

通过桥墩在不同工况下的刚度、强度和稳定性分析，对比3种空心截面桥墩的力学特性，其中刚度和强度分析是对比3种桥墩在最大悬臂工况时的应力、位移及极限承载工况的极限承载力结果，而稳定性则通过最大悬臂工况下的桥墩线性失稳结果和极限承载工况下不同桥墩所表现出的破坏模式来对比分析。

3.1 最大悬臂工况

3.1.1 应力

由图2可知，由于偏心弯矩，3种截面的桥墩内侧压应力均超过外侧2MPa以上。桥墩内侧的压应力均呈现“中间大、两端小”的趋势，而外侧压应力随着高度升高而降低。由于异厚截面桥墩内侧厚度比外侧大20cm，能更好协调曲线桥结构特性引起的内侧压应力，因此异厚桥墩内外侧应力偏差小。

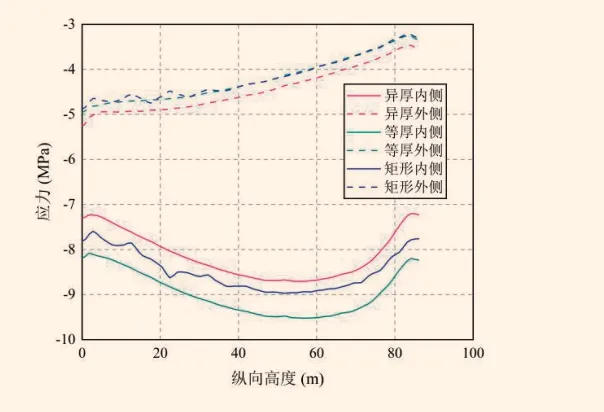
图2 不同桥墩沿纵向的压应力分布曲线

3.1.2 位移

在最大悬臂工况下3种桥墩的竖向位移如图3所示，可知桥墩内侧竖向位移则大于外侧，最大偏差为等厚截面墩顶的9.3cm。不同桥墩内侧竖向位移表现为八边形等厚截面＞矩形空心截面＞八边形异厚截面，与其应力大小规律一致。因此在最大悬臂工况下，八边形异厚截面桥墩能更好协调上部主梁的重心偏位特性，减少桥墩向内侧弯曲对主梁产生的不利影响。等厚截面和矩形空心截面的桥墩外侧竖向位移大小沿高度分布相近。

图3 不同截面桥墩竖向位移纵向分布

3.1.3 线性失稳

通过有限元计算不同截面形式桥墩的失稳模态，三种桥墩失稳规律相同，如图4所示（仅给出八边形异厚截面桥墩）：桥墩第一阶失稳模态均为沿着短轴（纵桥向）屈曲，表明该桥墩结构的短轴向变形大于长轴向（横桥向）变形，这是由于桥墩长轴向的截面刚度大于短轴向的截面刚度，长轴向稳定性更好；第二阶失稳模态是桥墩沿着长轴向屈曲；第三阶失稳模态是桥墩沿着长轴“S”形屈曲，与常规的桥墩失稳模态一致[8]。相应失稳特征值如表4所示，可知三种桥墩的前三阶失稳特征值无明显差距。这是由于在同一高度，等厚截面桥墩的惯性矩近似等于异厚截面桥墩，而矩形空心桥墩的惯性矩与异厚截面相等。

表4 不同桥墩的前三阶失稳模态

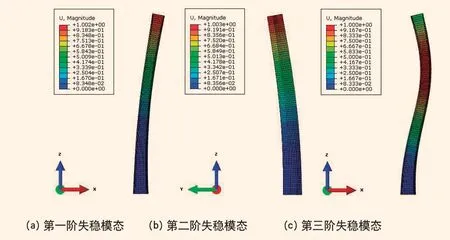
图4 八边形异厚截面桥墩的前三阶失稳模态

3.2 极限承载工况

3.2.1 破坏模式

采用位移和转角加载方式等效集中力和弯矩的作用，直至桥墩破坏，可将拉伸损伤dt≥0.8的区域视为混凝土破坏。由结果可知，在桥墩高度h的7/8和2/3处的长轴内外侧（平行于Y轴）同时形成两条分别上倾约50°、下倾约50°的裂缝，并向左右两侧扩展，如图5所示。所有桥墩的损伤均从内壁开始，且最终内壁损伤比外壁更严重。八边形异厚截面桥墩最终破坏程度最低，破坏区域主要在桥墩长轴。等厚截面桥墩的破坏模式和异厚截面相似，但损伤程度较大。这是由于异厚桥墩内侧厚度较大、受压面积大所造成，体现出其协调变形和承载的优势。矩形空心截面桥墩破损最严重，贯穿裂缝开度大，且裂缝两端沿着短轴扩展，最终导致桥墩破坏。

图5 不同截面桥墩的极限破坏模式

如图5所示，随着位移加载不同桥墩混凝土损伤体积变化规律相似，桥墩出现开裂的顺序为矩形空心截面＞八边形异厚截面＞八边形等厚截面，而最终破坏时损伤体积从小到大排序为八边形异厚截面＞八边形等厚截面＞矩形空心截面。

3.2.2 极限承载力

不同截面形式的桥墩在位移和转角加载时的荷载-位移曲线如图6所示。3种桥墩模型的荷载-位移曲线规律相似，桥墩承载力随着位移增大而增大，当位移加载超过一定值时，桥墩发生破坏，承载力达到极限值，随后承载力迅速降低。3种桥墩的极限承载力分别为358.3MN、342.1MN、346.9MN。采用八边形异厚截面的桥墩极限承载力比八边形等厚截面提高了4.7%，而矩形空心截面的桥墩极限承载力仅比八边形等厚截面提高了1.4%。

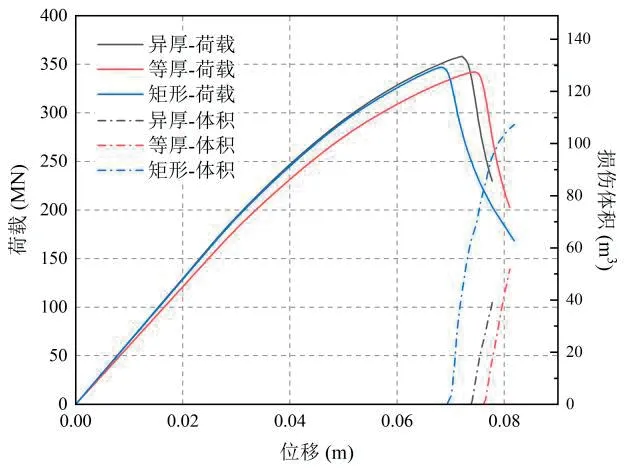
图6 不同截面桥墩的损伤体积变化与荷载-位移曲线

4 结束语

本文通过有限元计算，对比分析了不同截面桥墩在最大悬臂工况和极限承载工况呈现的力学特点，结论如下：在最大悬臂工况下，八边形异厚桥墩内侧的压应力和竖向位移最小，能更好地协调上部主梁的重心偏位特性，对上部主梁施工及成桥线形的影响较小；3种截面桥墩的前三阶线性失稳模态均为第一阶纵桥向屈曲，第二阶横桥向屈曲，第三阶纵桥向S形屈曲，且对应的失稳特征值基本一致；极限承载工况下，八边形异厚截面桥墩的最终损伤体积为矩形空心截面桥墩的1/3，其极限承载力超过等厚截面桥墩和矩形空心桥墩的3.3%。