数形结合，化抽象为直观

王小月

在七年级数学解题过程中，运用数形结合思想，能将复杂的数学知识变得直观简单，易于解题，提升解题质量与效率，同时也能促进我们对数学学习方法的掌握。

在七年级数学知识中，学习代数知识时可以利用数轴来进行解题，数轴是数形结合思想下的一个重要工具，可以将抽象且复杂的数学知识简单直观地呈现出来，促进我们对知识的深入理解，抓住知识的本质。因此，作为学生我们要养成作图的习惯，利用数轴来解决代数问题，从而来将数形结合思想贯穿在解题过程中，以比较有理数的大小为例。

例1

比较4、-1.5、0、1、-2这几个有理数的大小，我们可以利用数轴的方式，将这组数字在数轴上呈现出来，先画一个数轴，之后在数轴上将这些数字标记出来，根据右边的数字大于左边数字的原则来判断出答案：-2＜-1.5＜0＜1＜4。

例2

若a＜0，b＞0，且|a|＞|b|，试比较a，-a，b，-b四个数的大小。

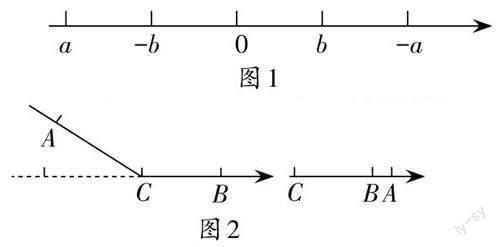
针对此例题的解法，若是我们单纯进行题目的思考，很难发现其中的规律，在解题中也将存在很大困难。这时我们可以利用数轴的方式将四个数展示出来：如下图1，我们先将a与b在数轴上标注出来，之后利用相反数的知识，将-a以及-b的位置，这样我们在数轴图像的观察中将十分清晰地了解到这四个数的大小关系，有效提升了我们的解题效率。

例3

在一条可以折叠的数轴上，A，B表示的数分别是-16，9，如图2，以点C为折点，将此数轴向右对折，若点A在点B的右边，且AB=3，则C点表示的数是______。

在对本题的解法中，要先观察数轴，仔细分析，根据A、B表示的数求出AB值[AB=9-（-16）=25]，之后在经过折叠之后根据AB值求出BC值（BC=[25+32-3=11]），以此来最终确定出C点所代表的数值是-2（9-11=-2）。

因此，我們要有效运用数形结合思想来进行解题，将复杂抽象的数学知识变得直观化以及简单化，让我们更容易理解数学知识中的本质内容，从而来提升自身的解题能力以及数学思维素养。

指导教师：张春明