蜡烛火焰耦合振荡的研究

2023-09-05宋家乐王雅萍苏一恒林彤彤

合肥工业大学学报（自然科学版） 2023年8期

方莲, 宋家乐, 王雅萍, 潘刚, 苏一恒, 林彤彤

(1.合肥工业大学基础部,安徽宣城 242000; 2.合肥工业大学土木与水利工程学院,安徽合肥 230009; 3.合肥工业大学计算机与信息学院,安徽合肥 230601)

0 引言

彼此邻近的蜡烛燃烧时能观察到振荡的火焰,这种振荡可以相互耦合,产生丰富的动力学行为。20世纪40年代至今已有多篇文献对蜡烛火焰的振荡与不稳定性、蜡烛间距不同对应的2种同步模式、拓朴结构耦合系统的振荡模式、同相与反相同步振幅衰减和相位差、蜡烛火焰的频率和相位特性等内容进行探讨[1-9],但在影响蜡烛耦合振荡因素上的结论仍存在一定的争议,需要进一步研究讨论。

本文在已有研究的基础上,探讨不同直径的2组全同蜡烛火焰之间的耦合振荡情况,得出2组全同蜡烛同相和反相振荡与距离的关系、振荡频率与蜡烛组间距之间的关系、蜡烛组直径不同对耦合范围的影响,并结合实验仿真情况讨论热辐射、热对流在耦合中的作用,明确了热对流是蜡烛耦合振荡的主导因素,并从涡动力学角度对耦合振荡机理给出解释。

1 理论分析

2组蜡烛火焰之间有3种可能的传热形式,即热扩散、热对流和热辐射,其中热扩散的影响微弱[3],因此考虑蜡烛火焰振荡主要是热对流和热辐射共同作用的结果。

根据能量守恒和氧平衡方程,对于单组蜡烛火焰振荡,其振荡过程的方程表达如下:

(1)

(2)

其中:C为系统的比热容;h为表面传热系数;T0为外部环境温度;T为火焰温度;β为单位体积石蜡的燃烧产热;a为燃料供给率;n为蜡烛振子火焰中的氧浓度;E为活化能;R为摩尔气体常数;σ为玻尔兹曼常数;n0为外部环境中的氧浓度;n为蜡烛火焰中的氧浓度;k为通过对流供氧的速率;ω1为温度变化的特征频率;ω2为氧浓度变化的特征频率。

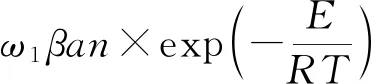
(3)

(4)

其中:μ为与气体的光吸收速率相对应的常数;i,j=1,2且i≠j。

为便于数值计算和仿真,将上述方程去量纲化:

最终得到:

(5)

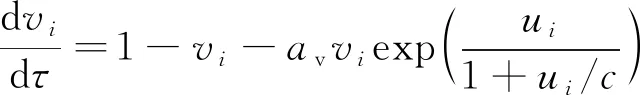
(6)

其中:i,j=1,2且i≠j;ui为第i组蜡烛组的火焰温度的无量纲化表示;vi为第i组蜡烛组周围氧气浓度的无量纲化表示;ε为与特征时间常量有关的一个常数;au、av为与燃料供给速率有关的量;σ0为与玻尔兹曼常数有关的常量;c为与能量有关的常数;μ0为耦合强度,μ0=μ/L2。

分析可知,耦合振荡主要与燃料供给率a和耦合强度μ0相关。常温常压下,蜡烛根数越多,蜡烛直径越大,则燃料供给率a越大,相应的au、av越大,振荡也就越强烈;耦合强度μ0则随着蜡烛组间距L变大而逐渐变小。

利用MATLAB软件对方程(5)、(6)进行时序仿真,结果如图1所示。图1中,纵、横坐标的量均无量纲,下同。图1a、图1b所示分别为“3+3”蜡烛组的同向振荡和反向振荡的仿真时序图。

图1中,当蜡烛组中蜡烛根数为3时,应当选取au=37、av=3.7。

图1仿真结果表明:蜡烛组间距较小时产生同相振荡,蜡烛组间距较大时产生反相振荡;此外,耦合振荡还与外部环境、蜡烛种类等因素有关。

2 实验探究

2.1 实验装置与条件

为了进一步探究耦合振荡的影响因素,本文设计了一系列实验。实验中所用到的物品包括多种蜡烛、燃烧实验箱、滑轨、高速摄像机(千眼狼2F04C,中国富煌君达公司)、长焦球面反射镜、计算机等。实验装置及数据处理系统示意图如图2所示。

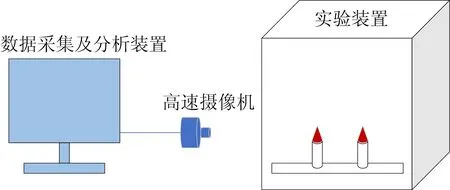
图2 实验装置及数据处理系统示意图

为使单组蜡烛振子的火焰可以聚拢为一束并形成振荡,实验中采用多支蜡烛捆绑方式,以蜡烛之间空隙最小的轴对称或中心对称形状进行排布,以保证蜡烛火焰最为紧密,最大限度地减小烛芯间距。同时,为了避免周围空气扰动的影响,在蜡烛组外围设置屏蔽装置。由于屏蔽装置较大而实验时间很短,屏蔽装置对实验的影响可以忽略不计。

实验在常温常压下、无风的燃烧实验箱中进行,2个蜡烛组可以通过水平滑轨上的移动改变相互之间的距离。

2.2 实验过程

实验内容主要分为以下4个部分:

1) 采用不同种类蜡烛,对不同烛心间距的蜡烛火焰高速摄像,确定蜡烛种类、耦合情况和变化范围。结果表明,选取较小直径的蜡烛(6 mm),在中心间距20～90 mm范围内进行实验,可以较好地满足实验要求。

2) 在蜡烛组之间设置薄膜,并初步判断传热形式。在2个蜡烛组之间引入一塑料薄膜,阻断了热对流影响后,仍能观察到耦合振荡现象;而引入锡纸膜,阻断了热对流和热辐射的影响后,则完全观察不到耦合振荡的现象。这初步表明耦合振荡是热辐射与热对流共同作用的结果。

3) 研究2组3根全同蜡烛振子(下文称为“3+3”)的耦合振荡。通过调节2个蜡烛组中心间距,从20 mm增加至90 mm,以2 mm为步幅进行多组重复实验。

4) 继续做“4+4”“5+5”“6+6”蜡烛组的多组实验,观察不同直径蜡烛组的耦合振荡现象。

下文以“3+3”为例,并附以“4+4”的相关数据进行对比。

3 实验结果与分析

3.1 实验结果

高速摄像机以500帧/s的帧率进行实验拍摄,并利用Origin软件进行图像处理,得到的数据及图像分别见表1所列和图3、图4所示。其中:表1所列为“3+3”“4+4”蜡烛组耦合情况与距离的关系;图3所示为“3+3”蜡烛组振荡频率与蜡烛组间距的关系;图4a、图4b分别为“3+3”蜡烛组同向振荡与反向振荡对应的亮度时序图,图4c、图4d分别为“4+4”蜡烛组同向振荡与反向振荡对应的亮度时序图。

表1 “3+3”“4+4”蜡烛组耦合情况与距离的关系

图3 “3+3”蜡烛组振荡频率与蜡烛组间距的关系

图4 “3+3”“4+4”蜡烛组同向和反向振荡对应的亮度时序图

对上述数据进行分析,可得到以下结论。

1) 两组蜡烛距离较近时,会出现同相振荡的行为;两组蜡烛距离较远时,会出现反相振荡的行为;两组蜡烛距离超出一定范围时,两组蜡烛振荡不相关。这是由于耦合强度μ0=μ/L2,当L增大时,μ0减小所致。在仿真中改变μ0的值,可以得到相应的同相或反相振荡,如图1a中μ0=0.50和图1b中μ0=0.01时的情况。

2) 在同相-反相-不相关的变换交界处,会出现2种模式之一或波动的现象。这证明耦合的变化是连续的,可以用连续函数表示。

3) 在其他实验条件一定的情况下,蜡烛直径越大,蜡烛根数越多,相应的燃料供给率a就越大,振荡的耦合范围就越大,振荡频率也越快,表1和图4均可得到此结论。

4) 对于不同种类的蜡烛,虽然耦合情况随间距变化的规律一样,但其并不完全相同。这主要是由于所选蜡烛种类不同导致燃料供应率a不同所致。

5) 以“3+3”为例,两组蜡烛的振荡频率与蜡烛组间距的关系为:当2个蜡烛组间距L≤30 mm时,产生同向振荡,振荡频率随距离的增大呈递增趋势;当35 mm≤L≤60 mm时,产生反向振荡,振荡频率随距离的增大呈递增趋势,如图3所示。

以上结论与方程(5)、(6)计算的结果相对应,说明仿真结果与实际变化趋势一致。

3.2 热对流在蜡烛火焰耦合振荡中的作用

为讨论热辐射和热对流对蜡烛火焰耦合振荡的作用,尝试在仿真中忽略辐射耦合项或对流散热项,再观察仿真中蜡烛耦合振荡的情况。方程(5)、(6)忽略辐射耦合项、对流散热项对应的时序仿真图如图5所示。

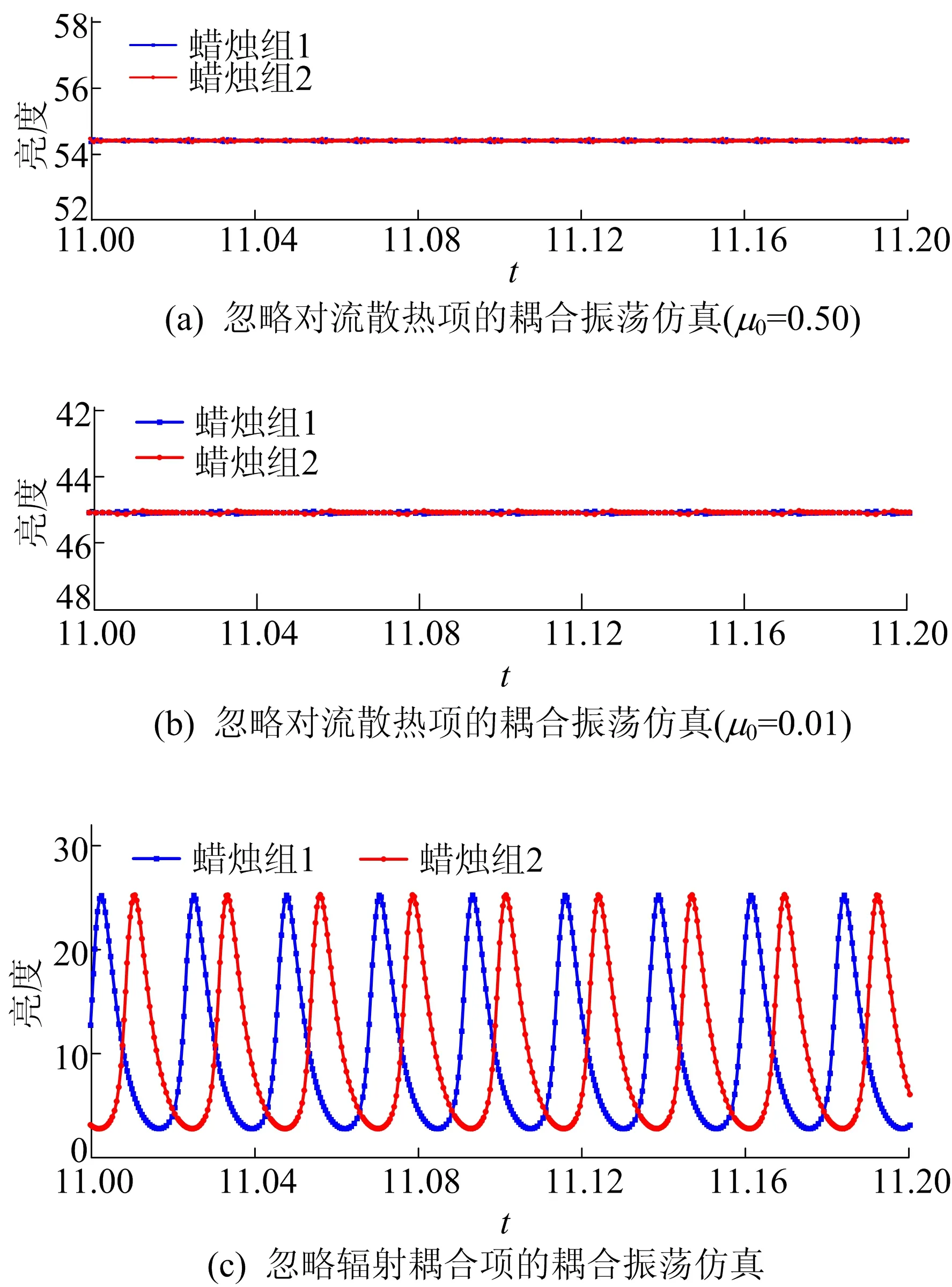
图5 方程(5)、(6)忽略辐射耦合项、对流散热项的时序仿真图

从图5a、图5b可以看出,在仿真中忽略对流散热项,则耦合振荡无法产生,仿真曲线近似一条直线。

从图5c可以看出,在仿真中忽略热辐射耦合项,蜡烛组仍然存在耦合振荡。

热辐射在耦合振荡过程中的作用体现在辐射耦合项上。当蜡烛组间距变化时,通过改变μ0值,热辐射能够在一定耦合范围内调节两组蜡烛的振荡相位差和振荡频率,但热辐射本身不足以使蜡烛组产生耦合振荡。

对于热对流和热辐射的共同作用,文献[3]研究认为热辐射是影响传热的主要因素。仿真结果表明:热辐射在耦合中确实起到一定的作用,但并非占据主导作用,热对流才是影响蜡烛耦合振荡的主要因素。

为了更直观地探究热对流的影响,本文研究了耦合振荡蜡烛组周围流场的特征。目前准确观测流场数值特征较为困难,因此采用纹影法[10]对蜡烛周围流场进行拍摄以定性分析。

纹影法拍摄的同相、反相振荡模式下的蜡烛流场如图6所示,反相振荡流场中的钝体如图7所示。

图6 纹影法拍摄的蜡烛组振荡火焰流场

图7 反相振荡流场中的钝体

通过观察流场,可以发现:

1) 从图6a可以看出,同相振荡的两蜡烛组流场相融合,中间无明显的外界空气影响,此时2个蜡烛组的振荡与捆绑在一起的1个蜡烛组的振荡相类似。

2) 从图6b可以看出,反相振荡的两蜡烛组之间的流场较为独立,中间有明显的外界空气。这部分空气基本不随着蜡烛火焰的振荡而上下运动。反相振荡流场类似于卡门涡街[9]。两者的相似之处是2个反向旋转剪切层的涡流方向,且这2种流场都涉及到剪切层的结构从对称过渡到交错的过程。此外有研究表明[8],从同相振荡到反相振荡的转变通常在雷诺数在几十到几百之间发生,这也与卡门涡街的理论范围较为相似。因此可以认为中间的外界空气充当了钝体的阻碍作用,如图7红色部分所示。

3) 在同相振荡时,蜡烛火焰外边缘包络接近于同步,且内边缘包络几乎为竖直的线条;反相振荡时,蜡烛火焰外边缘包络存在一定的相位差,且内边缘包络多为弯曲的线条。

3.3 耦合振荡的机理解释

从涡动力学的角度,对蜡烛火焰耦合振荡机制进行探究。单组蜡烛火焰振荡的机制可以解释为:周围的低密度热气体在浮力的作用下向上加速,在火焰外部形成薄剪切层;剪切层从火焰底部开始向上卷成一个环形涡;环形涡不断增强,逐渐使火焰变形,形成细颈形;细颈折断,导致火焰夹断;分离的火苗在环形涡的带动下上升,其余部分进入下一周期循环,如图8所示。

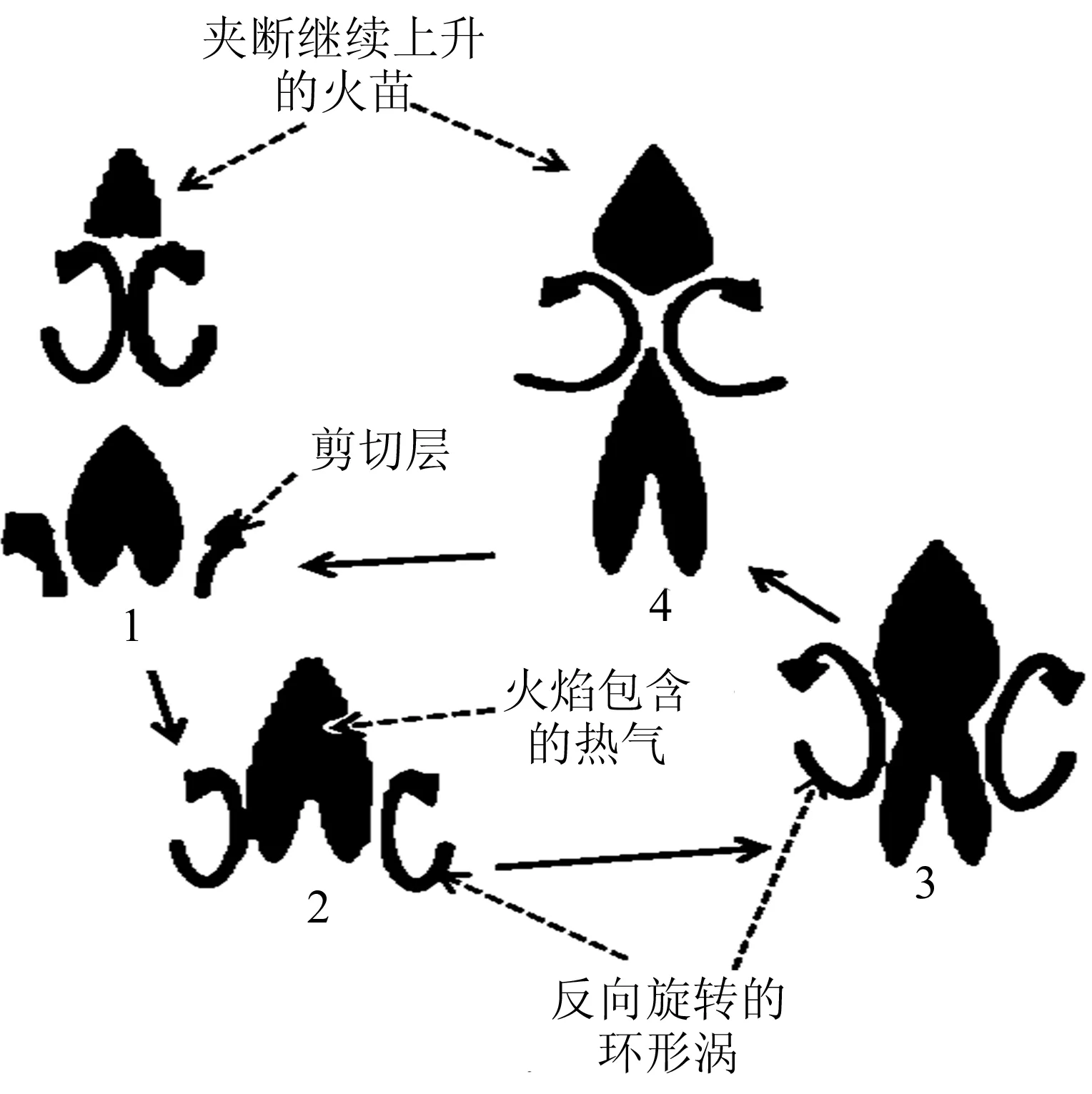
图8 单组蜡烛振子火焰周期性振荡

同相振荡蜡烛火焰的剪切情况如图9所示。从图9可以看出,2组同相振荡蜡烛火焰的剪切情况与单组蜡烛振子的剪切情况极为相似,环形涡旋的卷起均出现在2个火焰的振荡模式中。

图9 同相振荡蜡烛火焰的剪切情况

以上研究表明,对于单组蜡烛火焰振荡的机理可以推广到2组蜡烛火焰的振荡中。

在上述讨论的基础上,可以进一步解释同相与反相振荡的机制。“3+3”蜡烛组1个周期内同向与反向振荡的连续图如图10所示。

图10 “3+3”蜡烛组1个周期内耦合振荡连续图

在2个蜡烛组构成的系统中,火焰同相振荡时,2个火焰的内外边缘都发生变形,但内边缘变形小于外边缘;当火焰收缩到最小高度时,它们又回到最初的位置。在每个振荡周期中,2个火焰的发光部分从初始态开始同时向上伸长,直到达到最高火焰高度,火焰尖端的一部分被切断,最终变成烟雾,之后2个火焰同时收缩并恢复到初始状态,如图10a所示。

2个蜡烛组外剪切层的涡旋同步对称脱落,在外层剪切层上形成的旋涡的大小随着向上移动而逐渐增大。当这些旋涡向上移动时,它们同时拉长火焰表面直至达到最大火焰高度,此时这些旋涡相互接触,从而挤压2个火焰尖端的边缘,形成一团气流。这种旋涡的不断形成和运动导致火焰表面的反复伸长和收缩,从而产生同相振荡。

当火焰反相振荡时,一个火焰达到最高火焰高度时,另一个火焰处于最低火焰高度的位置,如图10b所示。

火焰的内边缘出现周期性变形,而外边缘则出现较小的波动。在外部和内部剪切层上都发生了旋涡脱落,一个振荡火焰周围形成的涡位于另一个振荡火焰周围形成的涡的上方。这种旋涡脱落的方式沿着火焰的内部剪切层,从而导致火焰的交替伸长和收缩。内部剪切层上的旋涡移动速度略快于外部剪切层,旋涡的内部由于周围热空气的自然对流而获得更多的流动速度,而外部由于周围冷空气而获得更低的流动速度,导致内部和外部的涡量有所不同,内部的涡量大于外部的涡量,从而产生反相振荡。