低信噪比下相位编码信号识别技术

邓杏松,徐文君,赵荣琦

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 引 言

当今战场的电磁环境日益复杂,相位编码、线性调频等非常规雷达信号不断增多。雷达信号调制特征识别能够为雷达信号分选提供有力的帮助,是实现雷达信号识别的重要手段。但是低信噪比情况下非常规雷达信号的特征提取和识别仍然存在问题,这是当前电子战研究领域的一个重要方向[1]。

目前,很多研究都已对相位编码信号的识别处理方法进行了研究。文献[2]采用对信号的瞬时相位或瞬时频率进行检测的方法进行相位编码识别处理,这一方法对信噪比要求很高。文献[3]通过构造相位跳变点样本,利用相关处理方法对相位跳变点进行检测,该方法具有一定的相关处理增益,但改善有限。文献[4]分析了利用小波变换检测调制信号的有效性,文献[5]提出了基于小波模值叠加的码速率估计方法,验证了在低信噪比下码速率估计的有效性。

本文给出了一种基于两级信道化结构和小波变换的调相信号检测方法,实现了低信噪比情况下相位编码信号的检测。利用信道化提高增益,使用信道化后信道内的零中频数据进行小波变换,避免检测相位跳变时的小波尺度盲区,通过检测小波变换模值的突变点进行相位调制特征识别。最终,将两级信道化的测量参数进行综合分析,形成脉冲描述字,保证了各参数的测量精度,提高了信号识别的适应性。

1 两级信道化设计与实现

信道化接收机是当前常用的满足电子战需求的宽带接收机结构,通过信道划分,将接收的信号从频域上分离,具有高频率分辨率、高灵敏度、能够处理时域叠加信号等优点[6]。信道化结构通过抑制子信道带宽外的噪声提升信号的信噪比。为更好地满足现代电子战对接收机高灵敏度的要求,本文设计了一种两级信道化结构以适应更低的信噪比。以瞬时带宽500 MHz、中频960 MHz的设计要求为例,本文以模数(AD)采样率为1.28 GHz进行两级信道化设计。

为保证信道化接收机的带内信号截获概率,本文采用50%交叠的信道划分方式,如图1所示。两级信道化结构采用串联方式,第1级信道化输入为AD采样的实信号,取信道数32,独立信道数为16,子带宽度为40 MHz,理论信噪比增益为12 dB。第2级信道化输入为第1级信道化选择的子信道数据。第2级信道化输入信号有效带宽为-40 MHz～40 MHz,取信道数8,独立信道数为8,子信道带宽为10 MHz,理论信噪比增益为9 dB。

图1 信道化信道划分示意图

本文设计的两级信道化结构采用系统稳定性好、能实现线性相位的有限长度冲激响应(FIR)滤波器,一级信道化的原型滤波器为192阶,二级信道化的原型滤波器为48阶,两级原型滤波器的幅频响应曲线如图2所示。

图2 原型滤波器幅频响应曲线

本文设计的两级信道化接收机的信号检测与处理流程如图3所示。首先,模数转换器(ADC)采样数据经过抽取送入第1级信道化子信道进行参数提取。然后,从第1级信道化子信道输出的16路信道数据中选取1路信号进行数据处理,同时将该路数据送入第2级信道化子信道进行处理。接着,从第2级信道化子信道数据中选取1路数据进行参数提取,并对选择的第2级子信道数据进行小波变换,根据小波模值的跳变情况完成调制类型识别,获取脉内特征。最后,将两级信道化的测量参数进行综合分析形成脉冲描述字。

图3 信号处理流程

2 相位调制信号的检测和识别方法

小波变换是一种线性时频变换,是分析非恒定信号和突变信号的有效方法。Haar小波对相位变化的短时信号具有较强的检测能力,非常适合探测信号的突变成分。文献[4]详细给出了使用Haar小波的相位调制信号的小波变换形式。处理相位编码信号,当Haar小波位于一个码元周期内部时,小波变换模值为:

(1)

当Haar小波位于码元跳变点处,小波变换模值为:

(2)

式中:A为信号幅度;T为码元宽度;wc为信号载波频率;β为相邻码元的相位差。

根据公式(1)可以看出,当小波窗位于码元周期内时,小波变换的模值是1个与频率有关的常数;如公式(2)所示,当小波窗位于2个相邻的码元之间时,该小波变换的模值出现1个峰值,即表明存在相位变化。因此可以根据小波模值实现信号相位和频率变化的检测。

对采样信号直接进行小波变换时,当wca为2π的整数倍时,公式(1)、(2)中的小波变换的模值为0,峰值消失,根据小波变换的模值无法判断相位变化,即存在小波尺度盲区。为此,文献[7]提出在进行小波变换前,将信号由中频变换为零频可以消除存在的无效小波尺度。即wc≈0时,公式(1)、(2)可转换为:

(3)

(4)

当n=iT,小波模值的峰值为:

(5)

公式(5)表明,将信号由中频转换为基带信号后,小波变换的峰值模值主要受小波尺度和码元间的相位差影响。小波尺度a在不大于码元周期的范围内,取值越大,小波模值越大,抗噪声能力越强;但根据公式(4),小波尺度a取值较大时,时间分辨率降低。本文取小波尺度a=2,以获得良好的时间精度。

两级信道化后,子信道内带宽为10 MHz,远小于采样时钟频率。根据上述将信号由中频变换为零频进行处理的要求,利用两级信道化后子信道内的数据进行小波变换恰好能满足小波变换前需要对数据进行频移的要求,从而避免了可能存在的小波尺度盲区。

3 参数综合处理流程

采样数据经过两级信道化处理后,对各级信道化数据的测量参数进行参数综合以形成最终的脉冲描述字,综合分析处理方法如图4所示。当第1级信道化和第2级信道化数据均存在有效信号时,由于两级信道化之前都进行了数据抽取,所以第1级信道化的时间测量参数具有更高的时间精度,信号脉宽和到达时间的测量更加准确;当第1级信道化处理结果存在有效信号、第2级信道化结果无有效信号时,表明信号持续时间很短,经过第2级信道化前的数据抽取后,信号无法被正确识别,所以选择第1级信道化的测量参数作为信号特征;当第1级信道化处理结果无有效信号、第2级信道化结果有有效信号时,表明信号强度较小,需要经过两级信道化的增益后才能被正确识别,因此选择第2级信道化的测量参数作为信号特征;当两级信道化处理结果均未检出有效信号时,则说明无有效信号。

4 仿真结果与分析

图5(a)为13位巴克码(1,1,1,1,1,0,0,1,1,0,1,0,1)调制的二进制相移键控(BPSK)信号在0 dB信噪比下的小波变换模值,图5(b)为13位泰勒四相码(0,1,2,3,0,3,0,3,0,3,2,1,0)调制的正交相移键控(QPSK)信号在3 dB信噪比下的小波变换模值,由上往下依次为采样数据直接进行小波变换的模值、第1级信道化后子信道数据的小波变换模值、第2级信道化后子信道数据的小波变换模值。图5表明,在低信噪比条件下,对采样数据直接进行小波变换,根据小波模值无法进行定位。第1级信道化后子信道数据的小波变换模值在部分位置出现了峰值,但与噪底的模值区分度不高,定位的准确性不高。第2级信道化后子信道数据的小波变换模值有明显的峰值,且噪底模值较小,能够进行准确的定位。

图5 小波变换模值图

为考察相位编码信号识别正确率随信噪比的变化情况,采用蒙特卡洛仿真法,选择小波尺度a=2,在各个信噪比下进行仿真试验,仿真结果如图6所示。根据BPSK信号识别率仿真曲线,当信噪比不小于-5 dB时,能保证识别正确率达到95%以上。根据QPSK信号识别率仿真曲线,当信噪比不小于-1 dB时,能保证识别正确率达到95 %以上。

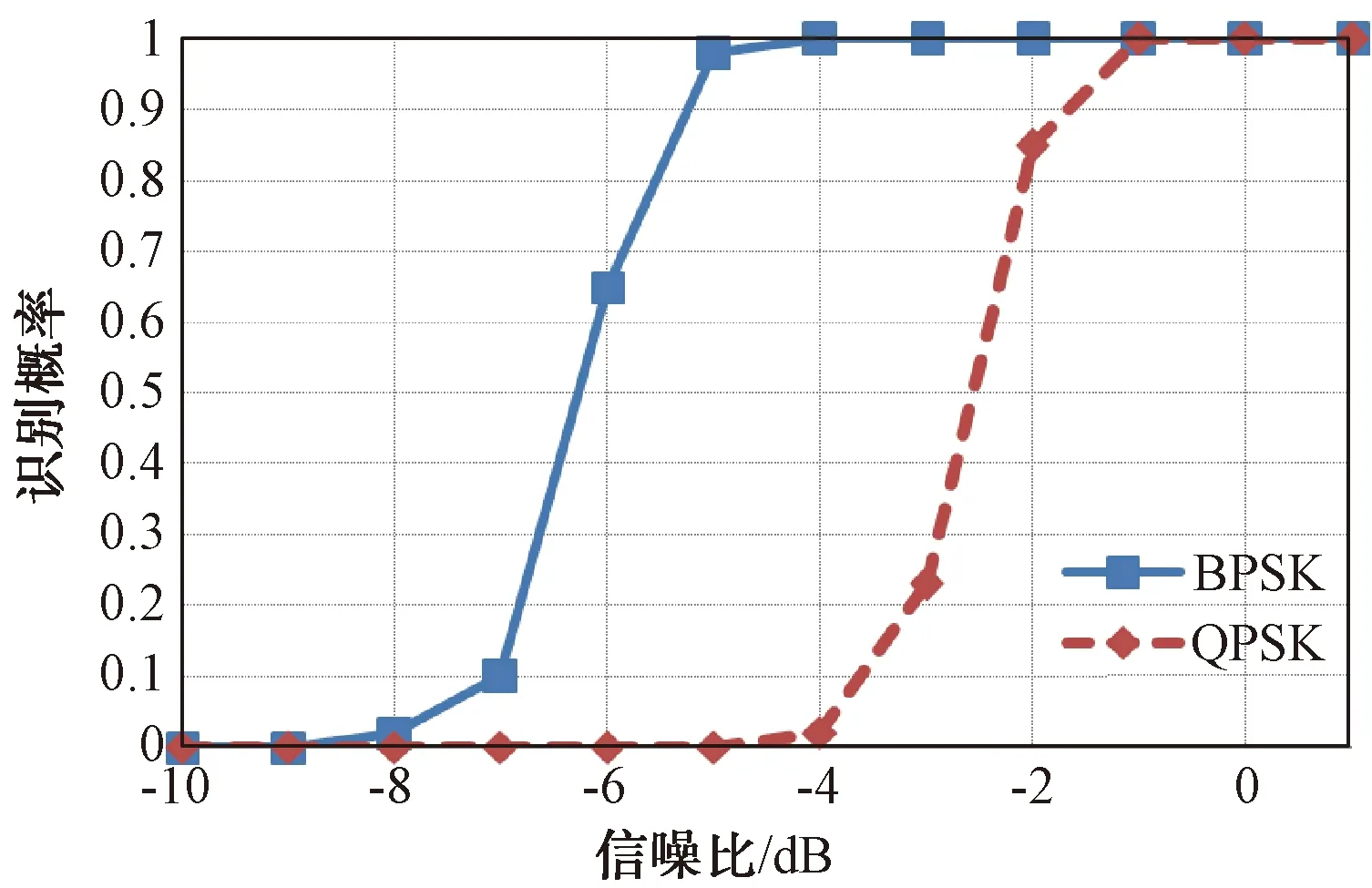
图6 不同信噪比下调相信号识别率

5 结束语

本文给出了一种基于二级信道化结构和小波变换的相位编码信号检测方法,实现了低信噪比情况下相位编码信号的检测。利用信道化提高检测灵敏度的同时,使用信道化后子信道内的零中频数据进行小波变换,避免了检测相位跳变时的小波尺度盲区,保证了单一尺度下使用小波变换模值进行相位跳变点检测的可靠性。仿真结果表明,两级信道化结构提高了信号检测的灵敏度,降低了调相信号检测对信噪比的要求,利用小波变换能够实现相位编码信号的正确检测。本文在数据处理过程中仅选择单一尺度进行小波变换,后续可以综合多尺度小波变换的结果进一步提高识别灵敏度和正确率。