基于低角补偿的雷达低空目标跟踪方法

2023-09-05王晓楠马振康

舰船电子对抗 2023年4期

王晓楠,马振康

(中国船舶集团有限公司第七二三研究所,江苏扬州 225101)

0 引言

随着战场威胁目标的发展和变化,以高速、机动反舰导弹为代表的“低、小、快”目标和以小型无人机为代表的“低、小、慢”目标,已经成为水面舰艇的主要威胁目标,是近程防御系统的主要作战对象。跟踪雷达是近程防御系统的重要组成部分,在承担系统反导防空使命任务时,其对目标的跟踪精度直接影响系统的作战效能,低角跟踪精度是跟踪雷达的核心指标之一[1]。

雷达对掠海目标进行跟踪时,发射波束在照射目标的同时会照射到海面,此时进入雷达接收机的回波包括直射目标回波和经过反射的目标回波。合成之后的回波中心将不再指向目标,会随目标高度和距离而起伏改变,假如不采取措施,雷达的目标跟踪精度会大幅降低,严重时可导致雷达无法正常跟踪目标。多径产生影响的大小与雷达发射频率、雷达架设高度、雷达的电磁波极化、目标高度、目标距离、海情等相关,是困扰雷达反导能力的复杂难题[2]。

本文提出基于低角补偿的雷达低空目标跟踪方法,根据已知参数对低角跟踪误差曲线进行仿真并拟合成补偿曲线,在低角跟踪过程中依据海情、目标的高度等信息引用仿真拟合曲线进行跟踪补偿,通过仿真计算,证明该方法可以有效提高雷达的低角跟踪精度。

1 多径模型及影响区域划分

1.1 多径模型[3]

采用球面多径反射模型来对多径条件下雷达对目标的跟踪进行分析计算。图1为球面多径模型示意图,图中雷达架设高度表示为hr,目标的高度表示为ht,直接路径表示为Rd,R1、R2一起构成反射路径,直接路径的仰角表示为θd,反射路径仰角表示为θr,入射余角表示为ψ。

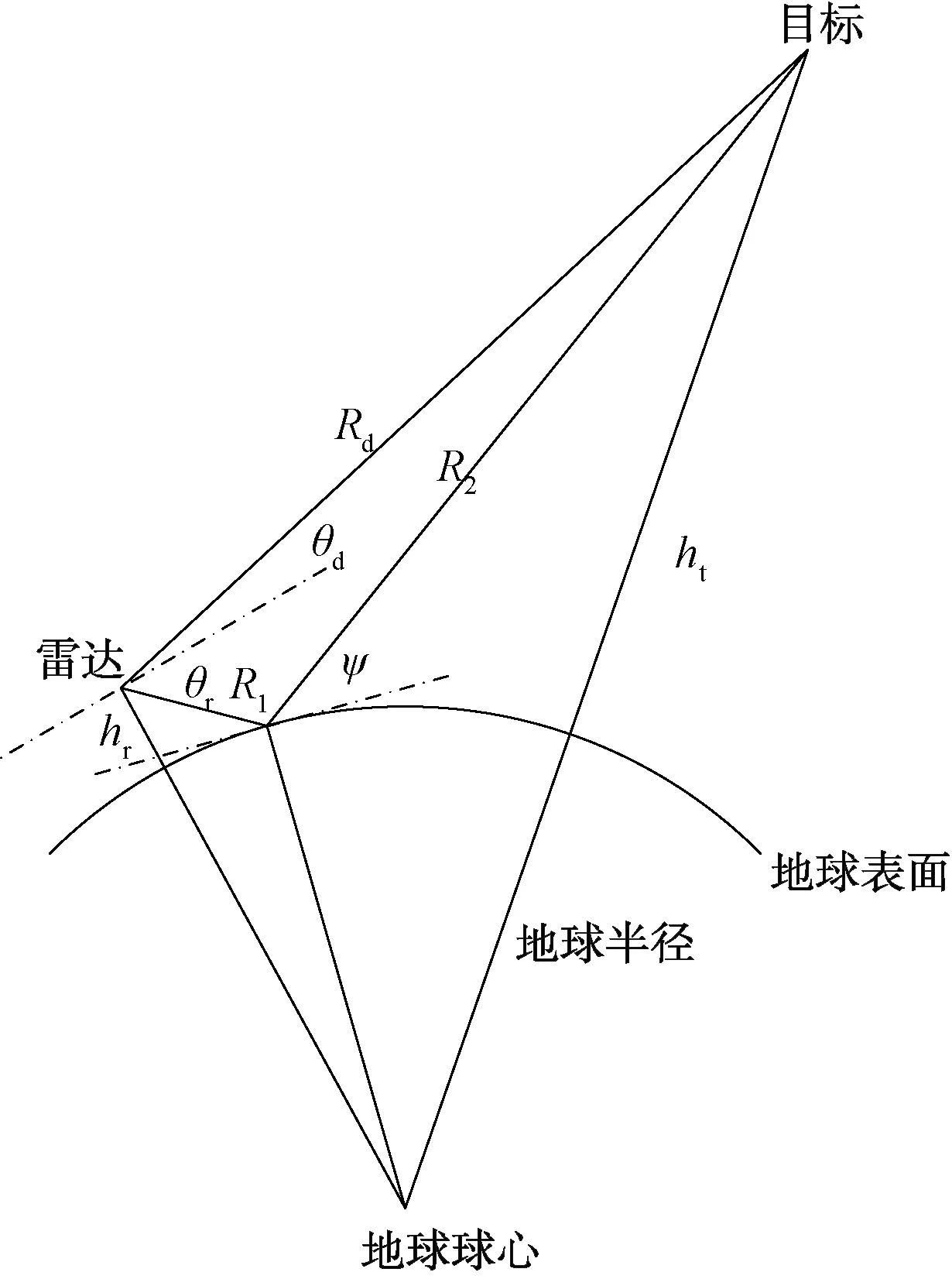
图1 球面多径反射模型图

直接路径Rd与反射路径R1、R2之间的区别导致了多径效应。由于2条路径区别较小,雷达通常无法区分,2条路径之间的波程差能够直接反映出多径效应。球面多径反射模型中2条路径间的波程差,需要首先采用中间变量法求解方程,再使用几何关系计算,能够得出球面反射模型中多径波程差为:

(1)

1.2 多径影响区域划分[4-5]

多径主要影响雷达对目标仰角的测量,在反射信号出现漫射现象时,方位也受到多路径的影响。多径对雷达低角跟踪的影响程度,取决于雷达天线波束“打地”的程度,按天线仰角的高低,大体分为3个区域:

(1) 副瓣区。雷达天线仰角的近副瓣照射地面/海面时,多路径影响程度与雷达天线副瓣电平大小有关。对于高精度跟踪雷达,在雷达仰角低于6倍波束宽度以下时,多路径影响开始逐渐凸显。

(2) 主瓣区。当雷达天线仰角低于0.8倍波束宽度时,雷达主波束部分“打地”,此时多路径影响开始变得严重,多路径测角误差基本上是目标的闪烁误差,需要采取多路径抑制措施,否则容易导致目标跟踪不稳定甚至丢失目标。

(3) 水平区。当雷达仰角接近0°时,目标直接回波信号与镜像回波信号幅度相当、相位相反,此时合成信号非常小,目标的检测将变得相当困难。

副瓣区的多径影响相对较小,跟踪雷达通常采用的频率捷变、偏轴跟踪等措施可以有效抑制副瓣区多径影响,保证雷达的目标跟踪精度。当目标进入主瓣区和水平区时,常规多径抑制方法对雷达低角跟踪的提升效果有限,需要采取其它有效措施来保证雷达的目标跟踪精度。

2 低角跟踪仿真分析[2,6-8]

以常用的单脉冲雷达为例,在多径条件下仰角测量误差信号为:

(2)

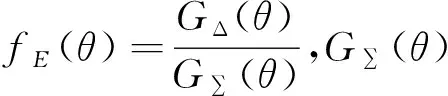
仿真条件设定如下:

海情设定为2级,目标高度为10 m、15 m,雷达架设高度为15 m,雷达工作频率为12～13 GHz,脉组频率捷变模式,频点数20,雷达波束宽度2°,重复频率8 kHz,32点快速傅里叶变换(FFT)积累,仿真距离3～10 km。

通过图2、图4仿真结果和图3、图5数据统计结果可以看出,雷达对超低空目标进行跟踪测量时受多径影响,目标跟踪精度较差。雷达对低空目标的仰角测量误差统计数据的统计结果如表1所示。

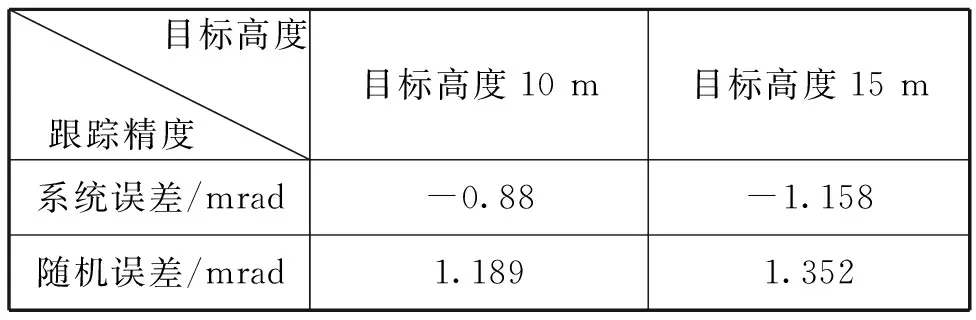
表1 雷达对不同高度目标的仰角测量误差统计表

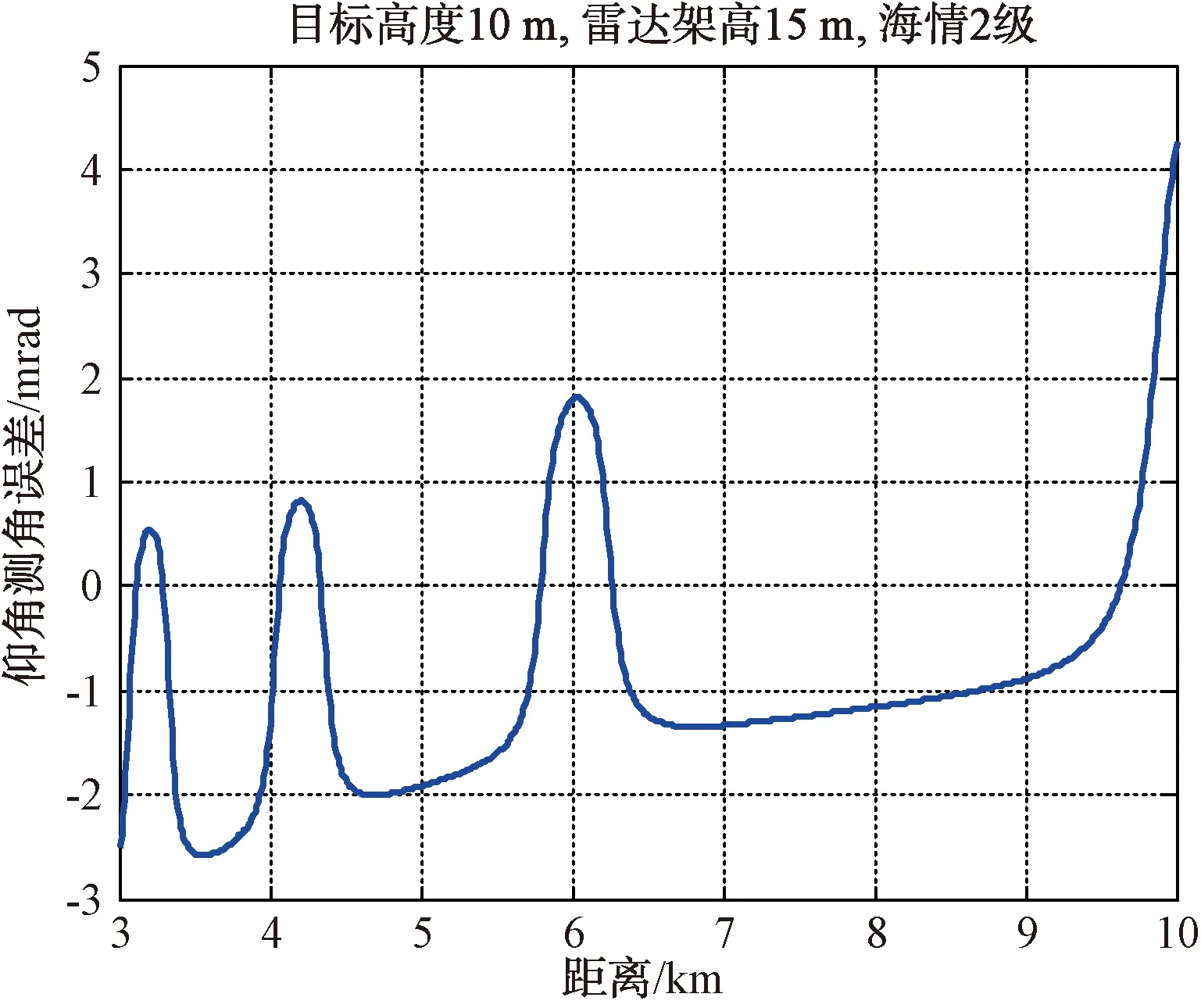
图2 雷达对高度10 m目标的仰角测量误差仿真结果

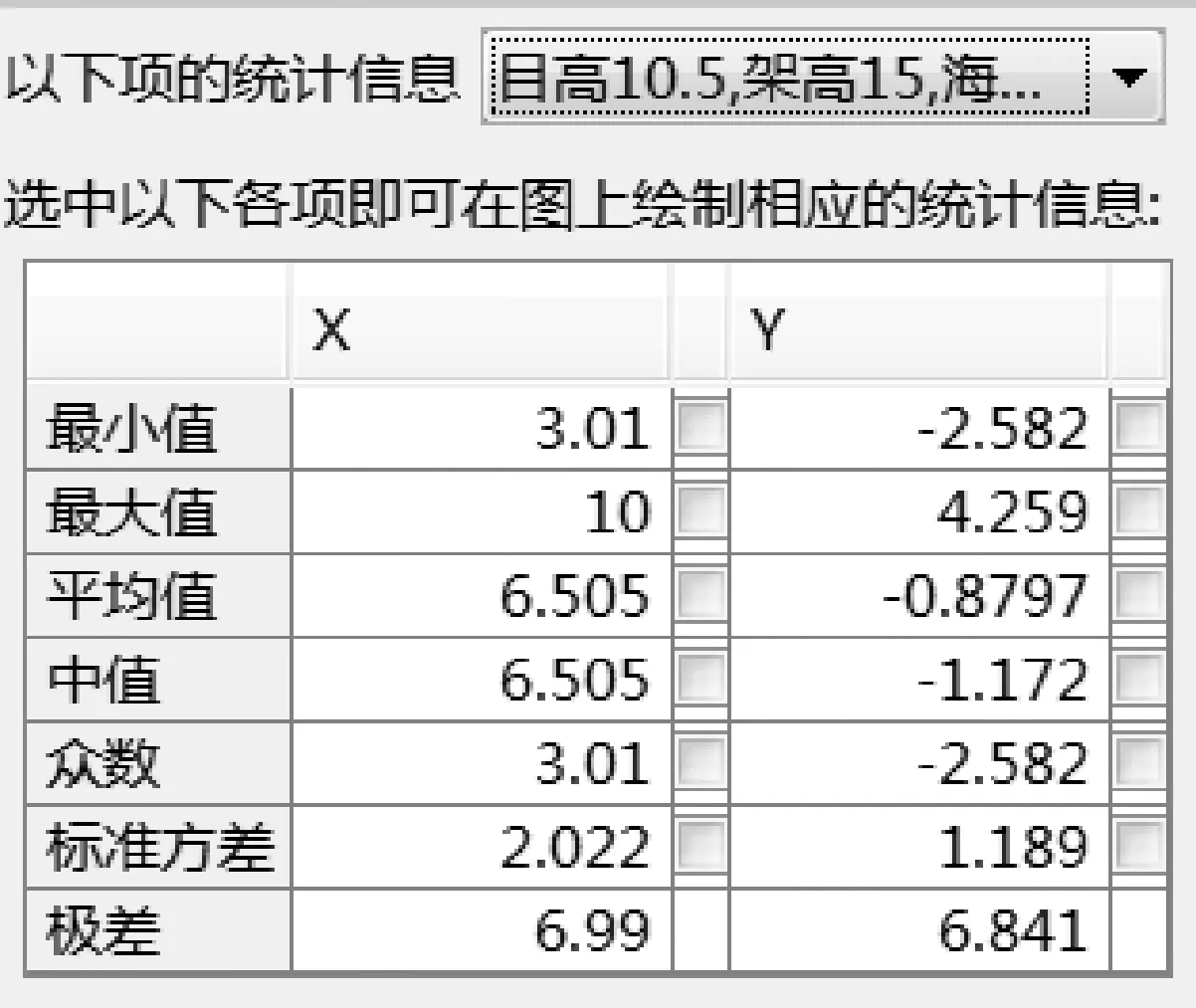
图3 雷达对高度10 m目标的仰角测量误差数据统计结果

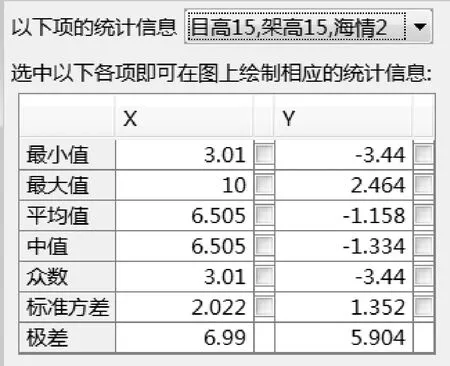
图5 雷达对高度15 m目标的仰角测量误差数据统计结果

通常近程反导武器系统要求跟踪雷达目标跟踪总误差优于1 mrad,确保系统的打击效能。根据表1统计的雷达对10 m、15 m高度的目标跟踪精度,均未达到指标,无法满足系统对低角跟踪精度的要求。

3 低角补偿设计

通过上述仿真结果可以看出,雷达在对低空目标进行跟踪时,仰角跟踪存在较大的偏差,其中系统分量较大。通过对跟踪仿真结果曲线进行拟合,将拟合曲线作为补偿曲线作用于目标跟踪过程中,理论上可以将系统误差去除并有效降低随机误差。将图2、图4雷达对低空目标的仰角测量误差数据进行二阶拟合,结果如图6、图7所示。

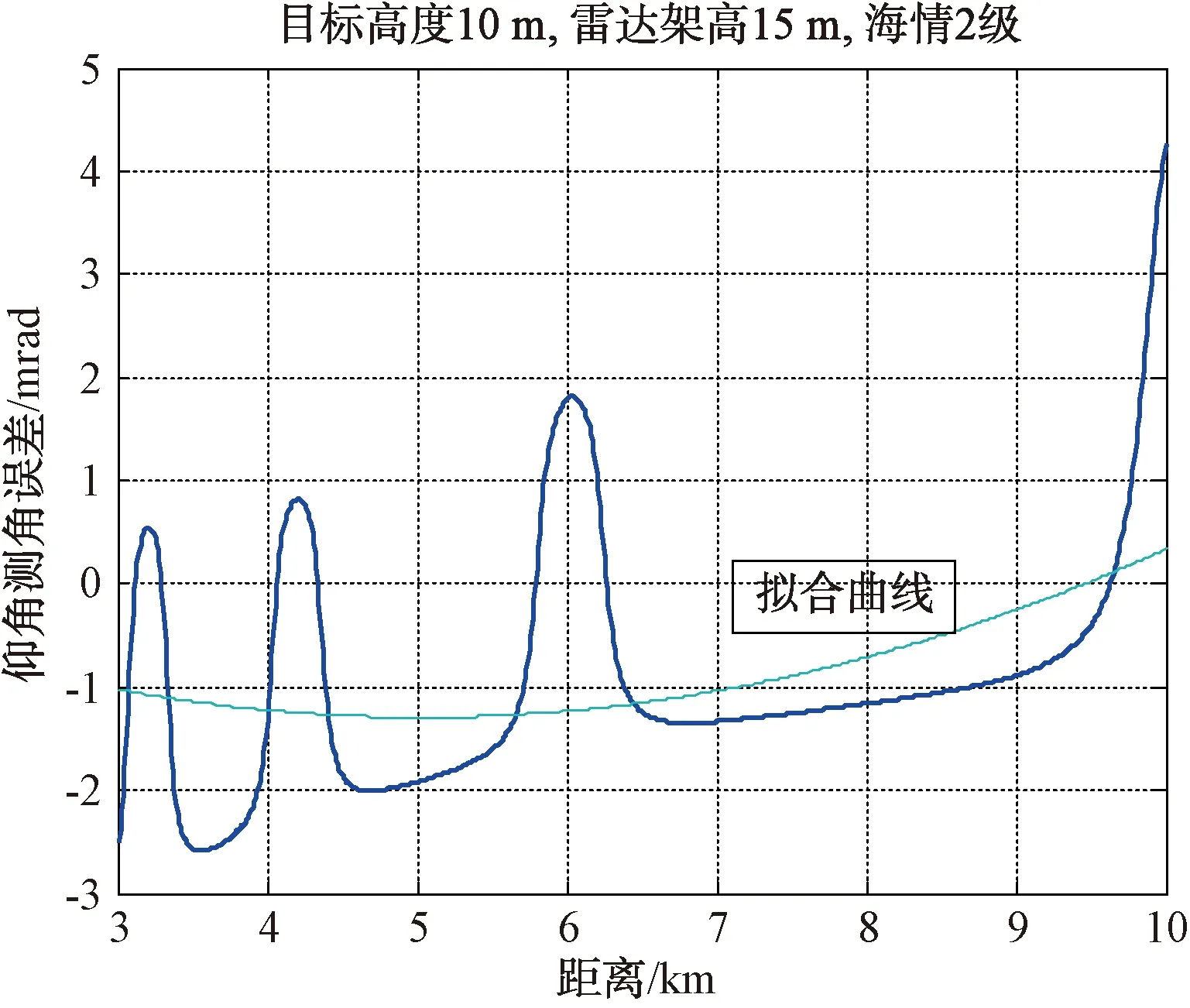
图6 雷达对高度10 m目标的仰角测量误差仿真结果及二阶拟合曲线

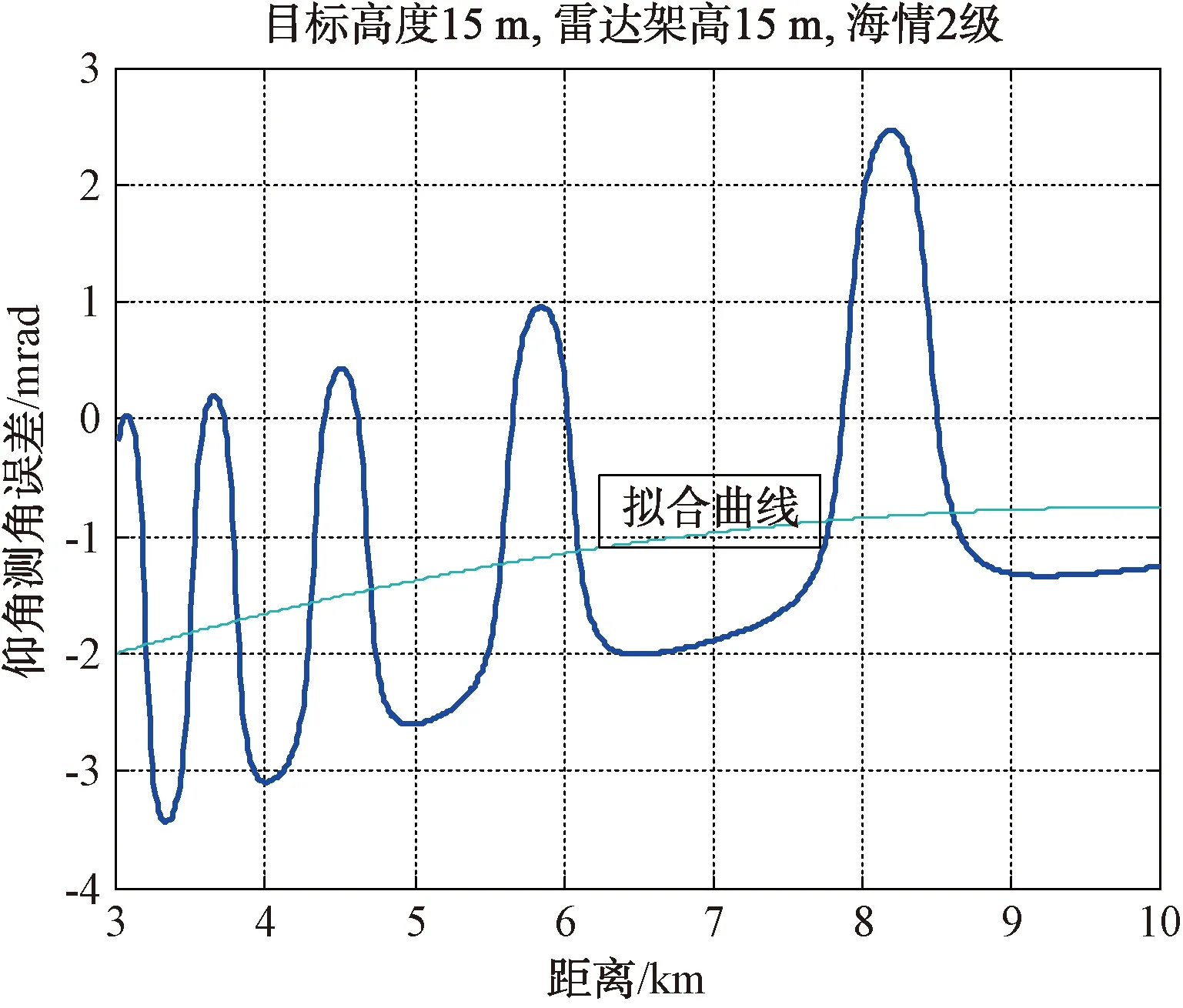
图7 雷达对高度15 m目标的仰角测量误差仿真结果及二阶拟合曲线

将对应补偿曲线作用于原始跟踪偏差中,理论上的剩余偏差仿真如图8、图10所示,对补偿后的仰角测量误差数据统计如图9、图11所示。

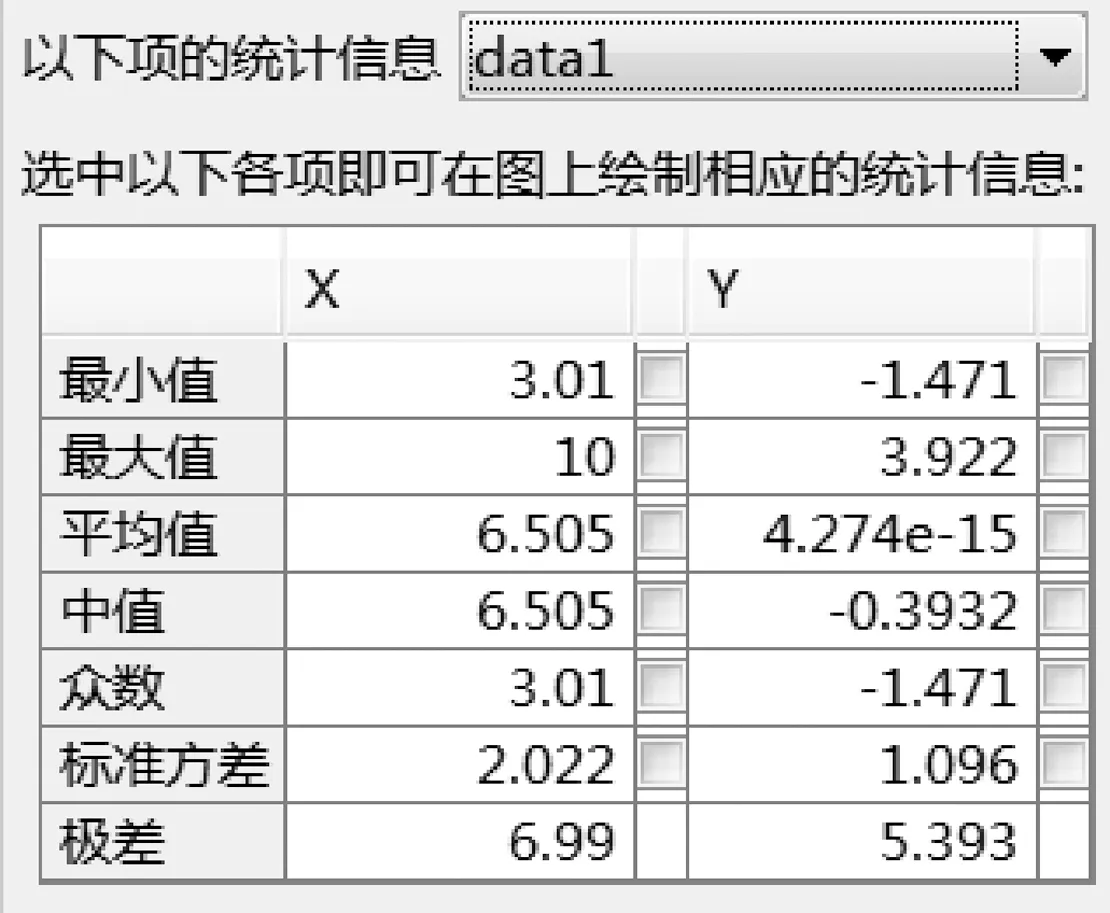
图9 雷达对高度10 m目标的仰角测量误差补偿后数据统计结果

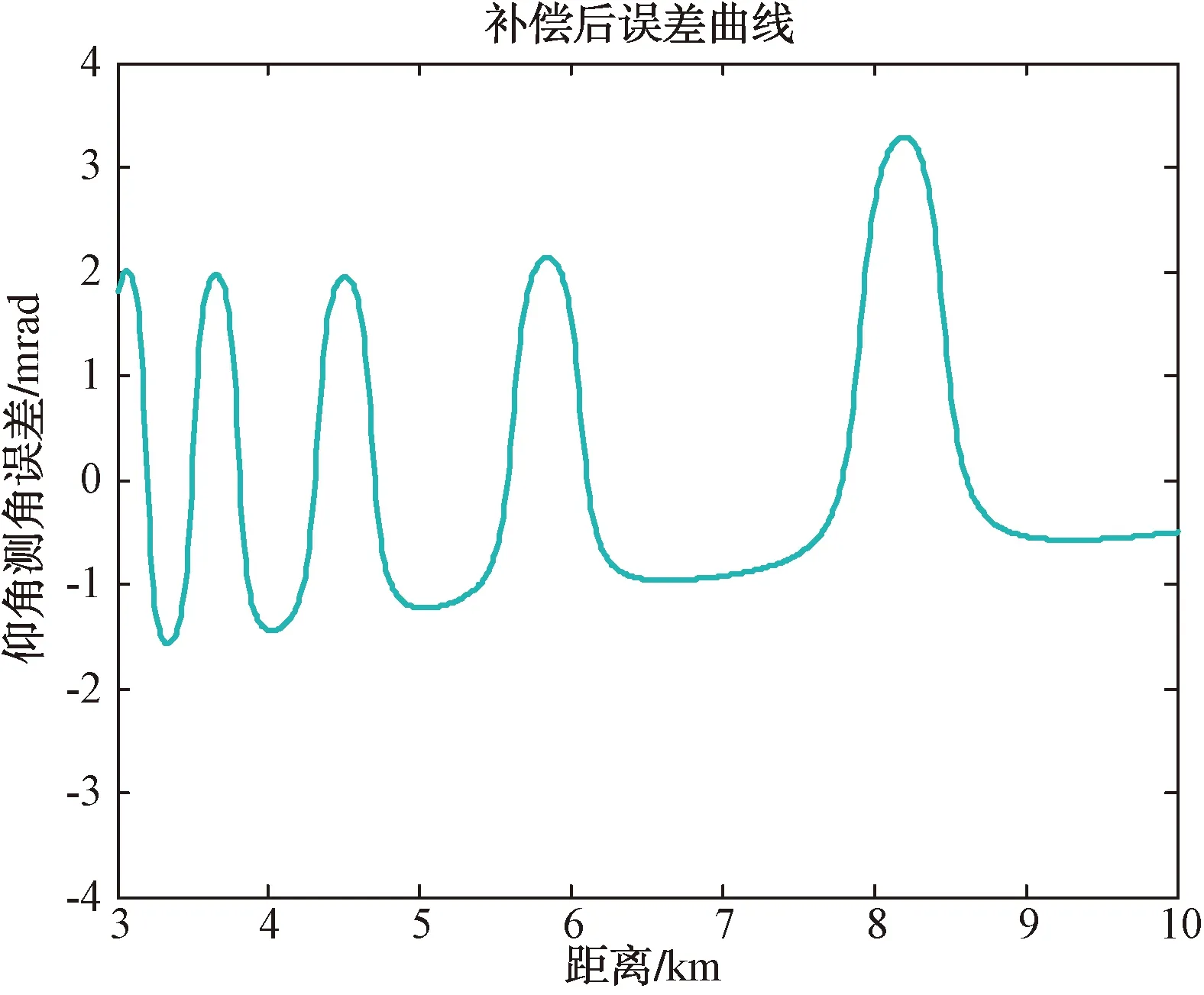
图10 雷达对高度15 m目标的仰角测量误差补偿后仿真结果

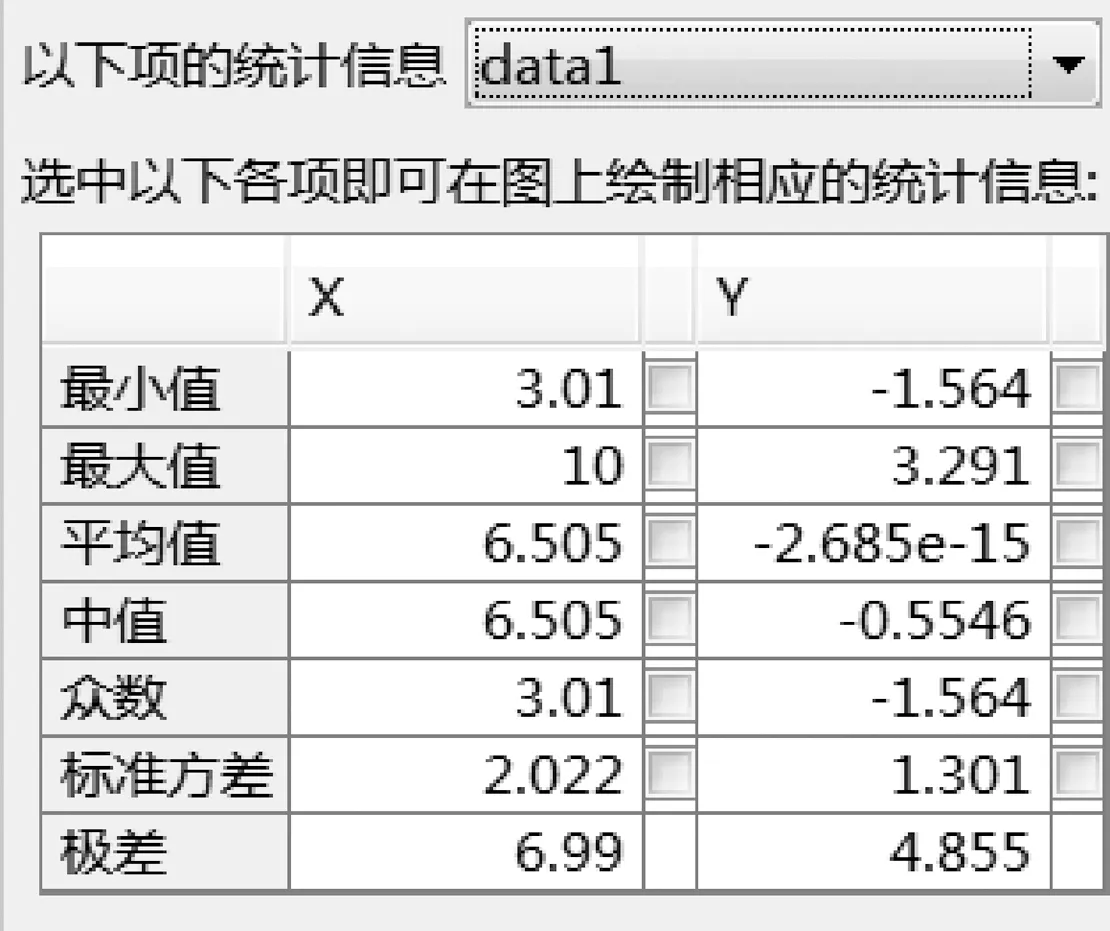
图11 雷达对高度15 m目标的仰角测量误差补偿后数据统计结果

对比图2～图11仿真结果,雷达对不同高度目标的仰角测量误差统计如表2所示。

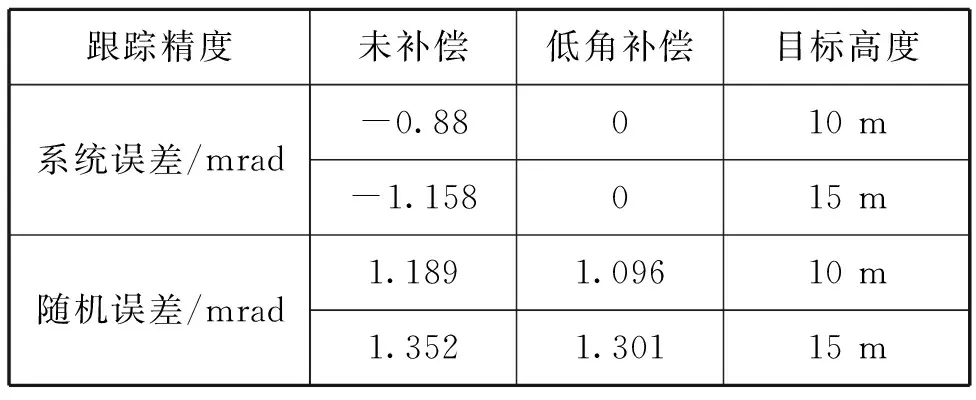
表2 雷达对不同高度目标的仰角测量误差统计表

通过表2可以看出,采取低角补偿后,理论上雷达低角跟踪的系统误差被抵消,对高度10 m目标的跟踪随机误差从1.189 mrad降低为1.096 mrad,对高度15 m目标的跟踪随机误差从1.352 mrad降低为1.301 mrad,目标跟踪的随机误差也得到改善,能够满足系统跟踪精度指标要求。说明采用基于低角补偿的雷达低空目标跟踪方法对多径效应引起的测角偏差进行补偿后,能够有效提高雷达低角跟踪精度。