天基空间目标监视中转台伺服控制系统的设计

谢妮慧 于飞 李晓 张晗 鄢南兴 李寅龙

天基空间目标监视中转台伺服控制系统的设计

谢妮慧 于飞 李晓 张晗 鄢南兴 李寅龙

（北京空间机电研究所，北京 100094）

为了实现高精度目标跟踪，研制了一套以数字信号处理器（Digital Signal Processor，DSP）和现场可编程门阵列（Field Programmable Gate Array，FPGA）为双核心处理器的二维跟踪转台伺服控制系统。控制算法采用位置环和速度环的双闭环比例积分（Proportional-Integral，PI）控制，通过串联校正改善了开环系统的相角裕度和幅值裕度，提高了闭环系统的带宽，最终实现了二维转台高精度、低速平稳的控制。机构和控制器联合调试结果表明：对方位轴和俯仰轴分别做最大速度和最大加速度的正弦引导时，方位轴最大跟踪误差为0.006°，误差均方根值为3.25″；俯仰轴最大跟踪误差为0.005°，误差均方根值为3.24″。测试结果证明该控制系统能够实现二维转台的低速平稳运行，满足大型转台伺服控制系统的性能要求。

天基空间目标监视 二维跟踪转台 伺服控制 矢量控制 运动轨迹规划

0 引言

空间目标监视系统的主要任务是对卫星、空间碎片等重要空间目标进行精确探测与跟踪，确定可能对航天系统构成威胁的空间目标的尺寸、形状和轨道参数等重要特性，并对目标特性数据进行归类和分发。空间目标监视具有重要的军事价值，不仅可以确定潜在敌人的空间运动能力，还可以预测空间物体的轨道，对己方空间系统可能发生的碰撞和受到的攻击进行告警[1-2]。

高精度、高可靠性的二维跟踪转台控制技术是天基空间目标监视系统发展的关键技术之一。通过俯仰轴和方位轴两个轴的运动可实现对空间目标的全方位监测，以及大范围空间目标的搜索与捕获、目标的精确指向和锁定跟踪等任务。为了提高天基空间目标监视系统的探测和跟踪精度，需要开展高精度、高可靠性的转台跟踪伺服技术研究。

伺服控制系统是二维跟踪转台的控制核心，极大的决定了转台最终的跟踪性能[3]。以往大多数转台控制都采用以DSP为控制核心再配置外围电路的伺服控制系统[4]，或采用工业计算机以及扩展板，再自开发应用程序和驱动程序的伺服控制系统[5]。外围电路和扩展板的功能都相对固定，无法进行系统升级，缺乏灵活性。本文研制了一套基于浮点型DSP和FPGA的双核心处理器的二维跟踪转台伺服控制系统，充分利用浮点型DSP的数字处理能力和FPGA的高速、高可靠性的数据传输能力。32位浮点型DSP6701具有运算速度快、运算精度高、运算能力大等特点[6-7]，且采用C语言编程，调试方便，非常适用于调试过程中需要反复对算法进行修改完善的转台伺服控制系统。与DSP相比，FPGA通过硬件来实现软件算法，为并行处理逻辑，因此运算速度快、数据传输时延小、可靠性高；除此之外，FPGA还具有体积小、集成度高、功耗低、电路设计灵活等特点[8-9]。因此，采用FPGA来实现与外部接口的信号传输，一方面能分担DSP的工作任务，另一方面还能提高伺服控制系统的集成度、工作效率以及可靠性和安全性等。

1 伺服控制系统组成

二维跟踪转台的结构如图1所示，俯仰轴和方位轴的驱动电机均采用了永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）[10-11]，两个轴绝对角度值的测量采用了光电编码器，用于反馈转台位置状态，实现控制系统的闭环。伺服控制系统的硬件电路采用浮点型DSP加FPGA的架构设计，DSP主要根据角度反馈结果和角度指令完成运动曲线的规划、角速度的计算、控制算法的实现、PWM波信号占空比的计算等；FPGA主要实现与上位机的通信、反馈角度的采集和PWM波的产生、接收上位机发送的遥控指令并反馈转台的遥测信息。DSP与FPGA之间的数据传输如图2所示。

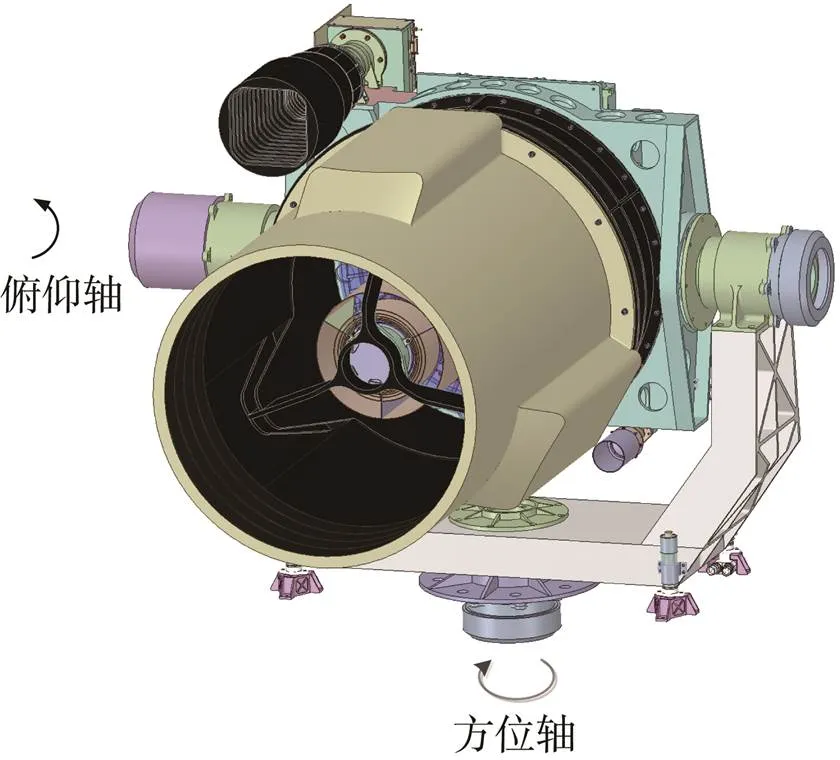
图1 二维跟踪转台结构

图2 FPGA与DSP之间的数据传输

本文采用了一种无电流反馈的永磁同步电动机转矩控制方法，应用电压矢量控制方式代替传统的电流矢量控制[12-14]，无电流环的矢量控制结构如图3所示。在数字控制器中定时采集电机转子的机械角度，计算出转子的电角度，然后根据规划的期望目标角度、反馈角度以及位置环和速度环双闭环PI的控制算法，并采用串联校正提升开环系统的相角裕度和幅值裕度，从而提高闭环系统的带宽。通过控制算法计算出所需的交轴（轴）电压分量u，直轴（轴）电压分量u=0；图3中的速度反馈值并未采用专门的硬件检测，而是通过软件进行角度差分再加一个一阶低通滤波器的方式获得，计算值作为速度环控制器的速度反馈值；然后利用所需的交轴电压分量以及当前电角度进行轴系变换，计算出所需的电机三相端电压，，，最终通过PWM逆变器完成三相端电压的输出，实现电磁转矩的输出控制。应用开环电压矢量控制方式代替电流矢量坐标变换与电流反馈控制过程，无需使用电流传感器与电流可控的PWM逆变器，可在较宽的转速范围内实现良好的转矩控制效果，特别适用于电路可靠性要求较高、带宽低的精密伺服控制系统。

图3 转台伺服控制系统控制框图

2 伺服控制系统实现

2.1 输入角度指令的轨迹规划

转台的指向有两种工作模式，即程控指向和命令指向。命令指向是指收到指令后，控制转台运动到指令要求的任意位置，且运动过程平稳、冲击小、定位精度高，对运动时间不做特别要求。程控指向是指控制转台按照以固定频率更新的一系列角度指令进行步进指向，由于角度指令之间的时间间隔较短，因此要求转台响应快、跟踪误差小。为了适应两种工作模式的不同需求，分别采用了两种运动轨迹规划。程控指向时采用角速度恒定、角度按斜坡变化的匀速运动，运动过程时间短，能提高动态跟踪精度。命令指向时采用角速度加速和减速过程均为正弦波曲线的运动轨迹规划，由于起始段和结束段的角速度和角加速度都比较小，因此转台运动过程时间比较长，但是启动和停止过程都很平稳，冲击小。

根据转台运动的相对角度的大小来划分，正弦运动轨迹又包括两种情况：第一种情况是相对运动角度较大时，角速度先按照正弦曲线从0增加到最大值，然后采用最大角速度匀速运动一段时间，最后角速度按照正弦曲线逐渐减小至0，此时转台正好指向指令角度值；第二种情况是相对运动角度较小时，角速度先按照正弦曲线从0增加到最大值，然后按照正弦曲线逐渐减小至0，无中间角速度为恒值的匀速运动，角速度曲线为一个完整周期的正弦曲线，角速度减小为0时转台正好指向指令角度值。两种情况下，角度指令都为角速度指令的积分，角加速度为角速度的微分，此外还须满足角加速度及角速度最大值限制的约束条件，运动轨迹仿真结果如图4所示，从上往下依次为角度指令曲线、角速度指令曲线、角加速度指令曲线。

图4 运动轨迹规划

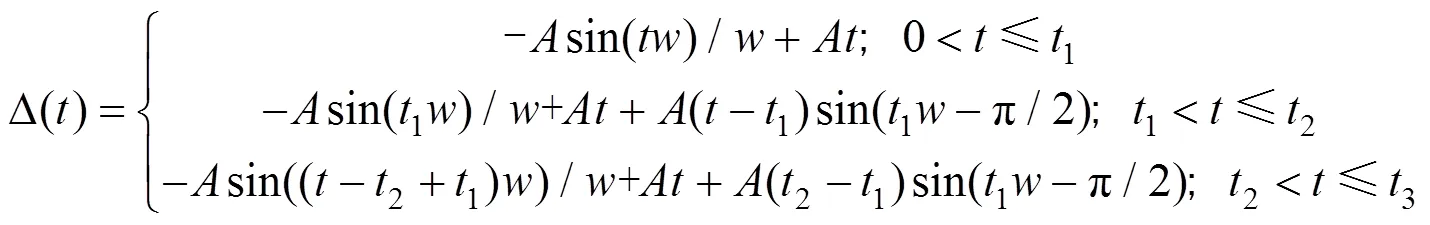
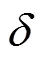
2.2 电压矢量控制及实现

矢量控制的基本思想是通过检测并控制电机三相定子的电流矢量，并根据转子磁场定向原理来达到控制三相电机的励磁电流和转矩电流的目的，从而实现了对三相电机的控制。具体的实现过程包括两步变换，即Clarke变换和Park变换，前者是采用将静止的、三相绕组变换为静止的两相正交的、绕组，后者是将静止的两相绕组变换成随着转子一起旋转的轴绕组与轴绕组[15-16]。如此，、、三相绕组产生的磁场矢量可以等效为轴和轴产生的磁场矢量，通过控制、轴定子电流分量即可控制、、三相绕组的控制电流，使电机转动。上述两步变换在数学上等同于坐标的旋转变换。永磁同步电机矢量控制坐标系如图5所示。

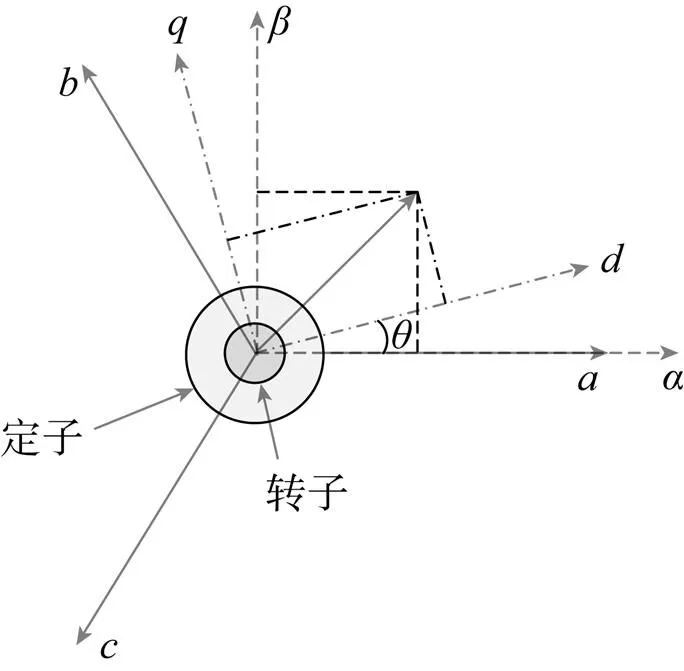
图5 永磁同步电机矢量控制坐标系

其中，Clarke变换公式为

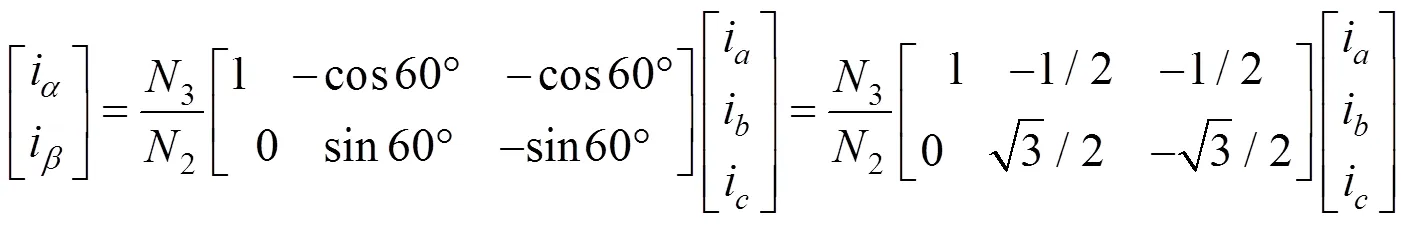
综上所述，对于含有单一可溶性 Cl和不溶性Cl样品的测定，采用 XFR方法所得的结果较为准确，可知XFR可以较准确地测量出单一原料中的总Cl含量；对于较为复杂的城市固体废弃物模拟组分中的 Cl测定存在较大的误差。利用热处理方式测Cl均存在不足之处，主要是原料燃烧不完全或吸收剂不能对所生成的氯化物全部吸收所致。因此，单一的方法较难满足城市固体废弃物中多种氯化物的Cl含量的测量。可见，知晓原料中的氯化物种类对找到较为合适的测Cl方法尤为重要。

Park变换公式为

式中为电机的电角度；i为轴电流；i为轴电流。

由此，从静止的、、三相绕组变换为随着转子一起旋转的、轴绕组的转换公式为

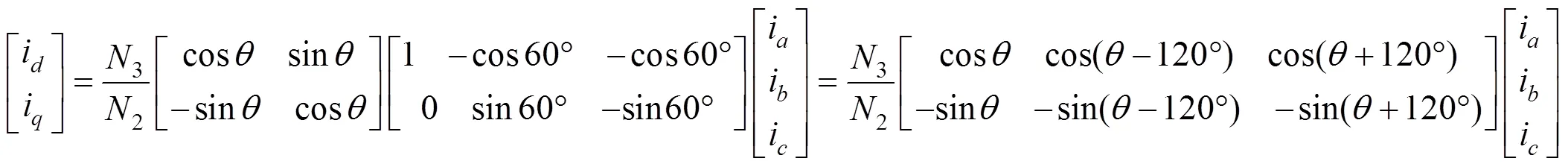
反变换为

i的磁场方向始终与转子的磁场方向相同，i的磁场方向始终与转子的磁场方向垂直，根据电磁感应定律，只有i方向产生的磁场才会对电机转子产生力矩，i方向产生的磁场做无用功，且会干扰转子的永磁铁产生的磁场，即转矩与i有关，与i无关，因此可采用i=0控制。此时，式（6）可进一步简化为

考虑到电路的复杂程度、电路的可靠性、元器件的等级、空间环境适应性等问题，本文简化硬件电路，省略掉电流环，采用电压，控制，用电压矢量控制方式代替电流矢量坐标变换与电流反馈控制过程，即“=0控制”变为“=0控制”，则、三相端的电压为

2.3 系统仿真及算法实现

永磁同步电机在旋转坐标系下的数学模型为[17-19]

式中为相电阻；L和L分别表示轴和轴线圈电感，为常数；为转子永磁体产生的定子绕组的磁链；r为转子机械角速度；r为转子电角度的角速度；e为输出转矩。由于面装式永磁同步电机交、直轴电感相等，即L=L=L，因此，式（8）中第三个方程可简化为

式中t为电流力矩系数，t=1.5；b为反电动势系数，b=；为电机转动惯量。

永磁同步电机及负载的参数如表1所示。

图6 永磁同步电机结构示意

表1 电机及负载参数

图7 双闭环控制器框图

闭环系统带宽越大，系统对输入信号具有更强的跟踪能力，但是对扰动输入信号具有较差的抑制能力，因此系统带宽选择应折中考虑，不能一味求大。根据相关研究，系统开环指标截止频率C与闭环指标带宽频率B有着密切的关系[20]，C大的系统，B也大，而系统的带宽越大，系统的响应速度也越快，因此C和系统响应速度存在正比关系，C可以用来衡量闭环系统的响应速度。为了使系统具有良好的过渡过程，通常要求相角裕度达到45°～90°，而欲满足这一要求应使开环对数幅频特性在截止频率附近的斜率大于–40 dB/10倍频程，且有一定宽度。因此，应用校正环节就是为了兼顾系统的稳态误差和过渡过程的要求[20]。

控制器的设计是从内到外，先设计速度环控制器，再设计位置环控制器。通过校正后，位置环开环系统的对数幅频和对数相频特性曲线如图8、9所示。通过MATLAB函数可以得到方位轴当前相角裕度为84°，幅值裕度为78 dB，俯仰轴当前相角裕度为86°，幅值裕度为74 dB。两个轴的幅频特性在截止频率附近的斜率均大于–40 dB/10倍频程，且具有一定宽度，闭环稳态和动态性能都较好。

图8 方位轴波特图

图9 俯仰轴波特图

2.4 控制器的数字实现

在连续系统中，PID控制器、串联校正环节、低通或高通滤波器等都可以采用式（11）的一个或者多个串联来实现。为了在数字控制系统（离散系统）中实现连续系统中的控制器，本文在软件的控制算法调试过程中，先通过仿真设计得到连续系统控制器的传递函数，然后采用Z变换法对传递函数进行离散化，建立控制器的离散数学模型，最后在软件中通过函数实现离散的控制算法。具体实现步骤如下：

1）通过仿真得到连续系统中某一阶控制器的传递函数()，公式为

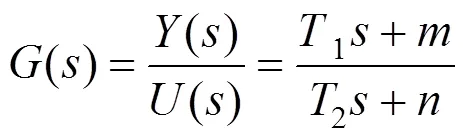
式中()和()分别表示输出量的拉氏变换与输入量的拉氏变换；1,2,,是与控制器相关的常系数。

2）采用Z变换法求得离散域的传递函数，公式为

式中0，1，0为离散化之后的常系数；()和()为输出量和输入量的离散拉氏变换，其中为离散系统下进行拉普拉斯变化的特殊变量。

3）将式（12）转换成差分方程，即

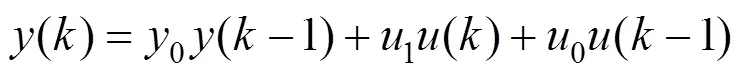
式中()，(–1)分别表示和–1时刻的输出；()，(–1)分别表示和–1时刻的输入。

式（13）通过迭代运算实现了连续系统中的一阶控制环节。控制系统中的其他控制环节包括PI控制器、超前或滞后校正、一阶滤波环节等的的传递函数形式与一阶控制器类似，因此可以通过先对函数进行Z变换，然后再用式（13）进行迭代的形式在代码中实现各个控制环节。

3 系统验证

为了验证文章所设计的控制系统是否能实现要求的功能和性能要求，在系统的硬件和软件设计完成后与转台机构连接进行了联合调试。在软件中嵌入了相应测试代码，用于存储每个控制周期的测量角度和规划角度指令。通过上位机发送指令，让转台的两个轴指向到规定范围内的任意角度，两个轴分开测试。二维跟踪转台技术指标要求如表2所示。

表2 二维跟踪转台技术指标

Tab.2 Technical index of the two-dimensional tracking turntable

采用MATLAB软件利用采集到的数据绘制运动曲线，计算测量角度和角度指令之间的误差，根据性能需求调整相关控制参数后再次重复上述测试，直至最佳结果为止。通过测试，俯仰轴和方位轴都能伺服到要求范围的内任意角度。以方位轴从+70°伺服到–60°为例，跟踪曲线如图10（a）所示。指令规划采用最大速度为2.5（°）/s、最大加速度为1（°）/s2的正弦规划，最大跟踪误差为0.006°，跟踪误差的均方根值为3.24″；俯仰轴从+40°伺服到–80°的跟踪曲线如图10（b）所示，指令规划采用最大速度为2.5（°）/s、最大加速度为1（°）/s2的正弦规划，最大跟踪误差为0.005°，跟踪误差的均方根值为3.26″。

图10 跟踪曲线

上述测试结果证明，该伺服控制系统实现了二维转台方位轴和俯仰轴的高精度指向控制，最终精度满足俯仰轴和方位轴跟踪精度小于0.007°的技术指标要求，能够实现二维转台的低速平稳运行，满足大型转台伺服控制系统的性能要求。

4 结束语

本文研制了一套基于浮点型DSP和FPGA的双核心处理器的二维跟踪转台伺服控制系统，其中FPGA用于实现与上位机的通信、角度数据的采集和PWM波的产生；DSP用于实现数字控制器、永磁同步力矩电机的矢量控制、角速度的计算等运算量较大的工作任务，充分利用DSP出色的数据运算能力与FPGA高速高可靠性的信号传输能力。电机的运动控制采用了一种无电流反馈的永磁同步电动机转矩控制方法，应用电压矢量控制方式代替传统的电流矢量控制，无需使用电流传感器，可在较宽的转速范围内实现良好的转矩控制效果。转台伺服控制中控制算法采用了位置环和速度环的双闭环PI控制算法，通过前馈控制器补偿了扰动对系统的影响，并采用串联校正改善了系统的相角裕度和幅值裕度，最终实现了二维转台高精度、低速平稳的控制。机构和控制系统的联合调试结果表明：当对转台做最大速度为2.5（°）/s、最大加速度为1（°）/s2的正弦引导时，方位轴最大跟踪误差为0.006°，跟踪误差的均方根为3.25″；俯仰轴最大跟踪误差为0.005°，跟踪误差的均方根为3.24″。测试结果证明该控制系统能够实现二维转台的低速平稳运行，满足大型转台伺服控制系统的性能要求。

[1] 程瑞, 林喆, 张艾, 等. 基于相对运动的GEO目标精确成像跟踪方法研究[J]. 航天返回与遥感, 2020, 41(1): 56-63. CHENG Rui, LIN Zhe, ZHANG Ai, et al. Research on Accurate Imaging Tracking Algorithm for GEO Targets Based on Relative Motions[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 56-63. (in Chinese)

[2] 王雪瑶. 国外空间目标探测与识别系统发展现状研究[J]. 航天器工程, 2018, 27(3): 86-93. WANG Xueyao. Development Status Research of Foreign Space Target Detection and Identification Systems[J]. Spacecraft Engineering, 2018, 27(3): 86-93. (in Chinese)

[3] 杨鹏, 李晓, 赵鑫, 等. 高精度二维指向光电跟踪平台设计[J]. 航天返回与遥感, 2020, 41(4): 83-91. YANG Peng, LI Xiao, ZHAO Xin, et al. Design of a High Precision Two-dimension Pointing Electro-optical Tracking Platform[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(4): 83-91. (in Chinese)

[4] 黄令龙, 郭阳宽, 蒋培军, 等. 高精密伺服转台控制系统的设计[J]. 清华大学学报(自然科学版), 2004, 44(8): 1054-1056. HUANG Linglong, GUO Yangkuan, JIANG Peijun, et al. Control System for High-precision Turn Table[J]. Journal of Tsinghua University (Science and Technology), 2004, 44(8): 1054-1056. (in Chinese)

[5] 王海涌, 张为玮, 王卫. 多轴运动控制器在转台控制系统中的应用[J]. 电子技术应用, 2010, 36(3): 97-99. WANG Haiyong, ZHANG Weiwei, WANG Wei. Using PMAC in Motion Control System of Turntable[J]. Application of Elecrtonic Technique, 2010, 36(3): 97-99. (in Chinese)

[6] 孙文莉, 王海涛, 蔡磊. 基于FPGA与DSP的发动机参数采集系统设计[J]. 计算机测量与控制, 2019, 27(6): 186-189. SUN Wenli, WANG Haitao, CAI Lei. Design of Engine Parameter Acquisition System Based on FPGA and DSP[J]. Computer Measurement & Control, 2019, 27(6): 186-189. (in Chinese)

[7] 邓永停, 李洪文, 王建立, 等. 基于DSP和FPGA的望远镜伺服控制系统设计[J]. 红外与激光工程, 2014, 43(3): 908-914. DENG Yongting, LI Hongwen, WANG Jianli, et al. Design of Telescope Servo System Based on DSP and FPGA[J]. Infrared and Laser Engineering, 2014, 43(3): 908-914. (in Chinese)

[8] 王海霞, 曾成, 伍萍辉. 基于FPGA的高频整流SPWM波形发生器[J]. 电测与仪表, 2013(1): 94-97.WANG Haixia, ZENG Cheng, WU Pinghui. SPWM Generator in High Frequency Rectifying Circuit Based on FPGA[J]. Electrical Measurement & Instrumentation, 2013(1): 94-97. (in Chinese)

[9] 杜志传, 郑建立. 基于CPLD/FPGA的VHDL语言电路优化设计[J]. 现代电子技术, 2010(3): 191-193. DU Zhichuan, ZHENG Jianli. Optimized Design of Circuits in VHDL Based on CPLD/FPGA[J]. Modern Electronics Technique, 2010(3): 191-193. (in Chinese)

[10] 雷阳, 徐静, 郝强, 等. 基于带宽的永磁同步电机伺服控制器设计[J]. 南京理工大学学报, 2019, 43(6): 677-683. LEI Yang, XU Jing, HAO Qiang, et al. Design of Permanent Magnet Synchronous Motor Servo Controller Based on Bandwidth[J]. Joumal of Nanjing University of Science and Technology, 2019, 43(6): 677-683. (in Chinese)

[11] 贾红敏, 张立广, 闫曌. 基于改进自抗扰的永磁同步电机位置伺服系统[J]. 电机与控制应用, 2020, 47(10): 33-39. JIA Hongmin, ZHANG Liguang, YAN Zhao. Permanent Magnet Synchronous Motor Position Servo System Based on Improved Active Disturbance Rejection Control[J]. Motor and Control Application, 2020, 47(10): 33-39. (in Chinese)

[12] 陈子印, 林喆, 康建兵, 等. 基于滤波反步法的三相永磁同步电机伺服控制[J]. 控制理论与应用, 2017, 34(4): 515-524. CHEN Ziyin, LIN Zhe, KANG Jianbing, et al. Servo Control of Three-phase Permanent Magnet Synchronous Motor Based on Command Filtered Backstepping[J]. Control Theory & Applications, 2017, 34(4): 515-524. (in Chinese)

[13] 赵景波, 张高强. 永磁同步电机高鲁棒性控制器设计研究[J]. 计算机仿真, 2017, 34(7): 339-344. ZHAO Jingbo, ZHANG Gaoqiang. Design and Research of High Robust Controller for Permanent Magnet Synchronous Motor[J]. Computer Integrated Manufacturing Systems, 2017, 34(7): 339-344. (in Chinese)

[14] 任志斌, 朱杰, 周运逸, 等. 永磁同步电机目标位置调节的伺服控制系统研制[J]. 微电机, 2019, 52(9): 80-83, 97. REN Zhibin, ZHU Jie, ZHOU Yunyi, et al. Development of Servo Control System for Permanent Magnet Synchronous Motor Target Position Adjustment[J]. Micromotors, 2019, 52(9): 80-83, 97. (in Chinese)

[15] 祁超, 谢馨, 陈凌宇, 等. 精密转台S曲线轨迹规划及高精度控制[J]. 光学精密工程, 2018, 26(12): 2971-2981. QI Chao, XIE Xin, CHEN Lingyu, et al. S-curve Trajectory Planning and High-precision Control of Precision Servo Turntable[J]. Optics and Precision Engineering, 2018, 26(12): 2971-2981. (in Chinese)

[16] 王远竹, 胡金高. 伺服高速轨迹规划与精密跟踪控制的研究[J]. 微电机, 2017, 50(11): 35-38, 54. WANG Yuanzhu, HU Jingao. Research on Servo High Speed Trajectory Planning and Precision Tracking Control[J]. Motors, 2017, 50(11): 35-38, 54. (in Chinese)

[17] 赵真, 王碧, 陈国平. 空问站大柔性太阳电池翼驱动装置的滑模伺服控制[J]. 振动与冲击, 2020, 39(3): 212-218, 288. ZHAO Zhen, WANG Bi, CHEN Guoping. Sliding Mode Servo Control of a Large Flexible Solar Cell Wing Driving Device[J]. Journal of Vibration and Shock, 2020, 39(3): 212-218, 288. (in Chinese)

[18] 吕宏宇, 金刚石, 刘立志. 光电跟踪转台伺服控制策略研究[J]. 激光与红外, 2018, 48(4): 503-508. LV Hongyu, JIN Gangshi, LIU Lizhi. Research on Servo Control Strategy of Opto-electronic Tracking Turntable[J]. Laser & Infrared, 2018, 48(4): 503-508. (in Chinese)

[19] 于贵, 蒋辉雄. 直流电机数字调速软件的实现[J]. 电测与仪表, 2012, 49(5): 93-96. YU Gui, JIANG Huixiong. Realization of the DC Motor Digital Speed Control Software[J]. Electrical Measurement & Instrumentation, 2012, 49(5): 93-96. (in Chinese)

[20] 胡寿松. 自动控制原理简明教程[M]. 北京: 科学出版社, 2003. HU Shousong. A Concise Tutorial on the Principle of Automatic Control[M]. Beijing: Science Press, 2003. (in Chinese)

Space-Based Target Monitoring System Utilizing Turntable Servo Control

XIE Nihui YU Fei LI Xiao ZHANG Han YAN Nanxing LI Yinlong

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

In order to achieve target tracking with high precision, this paper develops a servo control system for the two-dimensional tracking turntable which takes DSP (Digital Signal Processor) and FPGA (Field Programmable Gate Array) as dual core processors. The control algorithm adopts the double closed-loop PI (Proportional-Integral) control algorithm including position and velocity loops. The phase angle and amplitude margins of the system are improved by the cascade compensation. Finally, the two-dimensional tracking turntable is realized with high precision, low speed and stable control. The joint debugging results of the mechanism and electronics show that when the turntable is guided sinusoidally with the maximum speed and the maximum acceleration respectively, the maximum guidance error of the azimuth axis is 0.006° with the root mean square value of 3.25", and the maximum guidance error of the pitch axis is 0.005° with the root mean square value of 3.24". The test results show that the control system can realize low speed and smooth operation for the two- dimensional tracking turntable and meet the performance requirements of large turntable servo control systems.

space-based target monitoring system; two-dimensional tracking turntable; servo control system; motor vector control; motion trajectory planning

TP311.3

A

1009-8518(2023)04-0048-10

10.3969/j.issn.1009-8518.2023.04.006

2022-08-13

谢妮慧, 于飞, 李晓, 等. 天基空间目标监视中转台伺服控制系统的设计[J]. 航天返回与遥感, 2023, 44(4): 48-57.

XIE Nihui, YU Fei, LI Xiao, et al. Space-Based Target Monitoring System Utilizing Turntable Servo Control[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(4): 48-57. (in Chinese)

谢妮慧，女，1986年生，2012年获北京航空航天大学控制科学与工程专业硕士学位，高级工程师。研究方向为遥感器机构控制技术。E-mail：524857918@qq.com。

（编辑：夏淑密）