考虑结构特征的采场胶结充填体稳定性分析
2023-09-05王冠男童大志汪杰
王冠男 童大志 汪杰
摘要:以阶段嗣后充填开采为背景,以胶结充填体为研究对象,基于莫尔-库仑破坏准则,综合考虑分层效应、顶部荷载、侧压系数等的影响,建立了大深宽比采场胶结充填体安全系数求解模型,并与其他学者的模型进行了对比验证,最后探讨各因素的影响特性。研究结果表明:滑动面位置存在位于第一分层、穿过2个分层和穿过3个分层等3种情形,且主要为前两种;对比其他模型,验证了本文模型的合理性与可靠性,不同模型研究背景不同,侧重点不同,结果存在一定差异;胶结充填体安全系数随顶部荷载、侧压系数和容重增大而减小,随内聚力、内摩擦角和内聚力比增大而增大,且它们之间均呈线性函数关系,其中安全系数对内聚力敏感度最高、对顶部荷载敏感度最低。
关键词:结构特征;嗣后充填;胶结充填体;分层效应;安全系数;稳定性分析
中图分类号:TD853.34文章编号:1001-1277(2023)09-0021-10
文献标志码:Adoi:10.11792/hj20230904
引 言
充填采矿法是将矿石开采所产生的废石和尾砂等固体废弃物与胶结剂和水按一定比例混合搅拌后回填至井下采空区的一种采矿方法[1-3],因而其具有安全性高、绿色环保等显著优势,应用比例逐年提高。阶段空场嗣后充填采矿法是空场采矿法与充填采矿法的有机统一,其兼具空场采矿法的高效率、低成本及充填采矿法的安全与环保,代表着未来大规模绿色采矿的发展方向[4-6]。
阶段空场嗣后充填采矿法通常将采场划分为矿房和矿柱。第一步回采矿房,然后采用尾砂胶结充填矿房采空区,且充填工序分为3步[7-9]:首先,在矿房采空区底部采用高灰砂比料浆充填,以形成较高的底部强度;然后,采用灰砂比相对较低的料浆充填矿房采空区中部,以降低充填成本;最后,再次采用高灰砂比料浆充填矿房采空区顶部。一方面减少充填体沉降以利于接顶,另一方面作为顶柱回采平台。第二步回采相邻矿柱,然后采用废石或尾砂非胶结充填矿柱采空区。当胶结充填体相邻矿柱采空区仅完成一侧充填时,胶结充填体一侧临空,另一侧受到相邻非胶结充填体的侧压作用,此时胶结充填体应力状态和稳定性最差,发生滑动失稳破坏风险最高。因此,研究此时胶结充填体受力特征及稳定性狀况具有重要现实意义。
国内外对采场胶结充填体稳定性的理论研究始于20世纪80年代,LI等[10-12]基于莫尔-库仑破坏准则,建立了胶结充填体的小深宽比稳定性评价模型,但其并未考虑胶结充填体的分层效应。MITCHELL等[13-14]针对胶结充填体一侧临空的情形,提出了一种基于极限平衡法的安全系数解析计算模型,此模型考虑了胶结充填体与围岩的接触黏结作用,但其后壁为围岩,胶结充填体不受侧压作用。刘光生等[15-16]提出了4种胶结充填体安全系数和强度需求的三维解析模型与方法,同样未考虑胶结充填体分层效应。张常光等[17]考虑了充填顺序及顶部超载的影响,建立了胶结充填体滑动失稳统一解模型,但认为胶结充填体会受到后壁非胶结充填体向上的黏结作用力。SMITH等[18]考虑了矿体倾角的影响,提出了单侧揭露倾斜胶结充填体强度需求模型,并推导了单侧揭露倾斜胶结充填体安全系数计算公式。LIU等[19]从阶段空场嗣后充填采矿法的采充时序出发,研究了非胶结充填体侧压作用对胶结充填体稳定性影响,修正了胶结充填体强度需求解析模型与方法。
综合上述研究可知,不同学者构建的胶结充填体强度模型研究背景不同,所考虑因素存在一定的差异,且通常不考虑胶结充填体的分层效应,而分层面的存在会改变充填体内部应力分布状态,劣化充填体整体强度,进而影响滑动失稳判定,但分层充填却能大大降低充填成本。
随着对充填工艺的精细控制,阶段嗣后分层充填正逐渐推广应用,针对完整充填体的强度模型已不能适应开采需要的问题,有必要构建一套适用于分层胶结充填体的稳定性判定模型。因此,本文基于莫尔-库仑破坏准则,以分层胶结充填体为研究对象,综合考虑分层效应、顶部荷载、侧压系数等的影响,建立了前壁揭露、后壁受压的分层胶结充填体安全系数求解模型,验证了模型的合理可靠性,探讨了各影响因素对安全系数的影响,并借助SPSS软件对复杂模型进行简化回归处理[20-21],以期能为现场应用提供一定的理论指导。
1 分层充填体三维强度模型构建
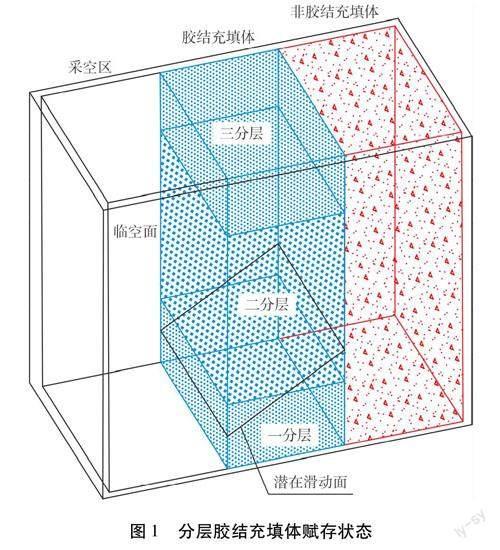
采场中矿房和矿柱分步回采,一步骤回采矿房,然后采用尾砂胶结充填体充填矿房采空区。通常,为节约充填成本,会采用分层充填,矿房胶结充填体会呈现三分层结构,其中底部和顶部分层配比较高,而中间层配比较低。二步骤回采相邻矿柱,矿柱回采完毕,通常进行非胶结充填,当一侧矿柱采空区充填完毕,而另一侧矿柱采空区还未充填时(见图1),分层胶结充填体不仅会受到自重应力的影响,而且还会受到相邻非胶结充填体的侧压作用,此时分层胶结充填体稳定性最差,研究此时分层胶结充填体的受力特征对于调整分层充填体结构和优化充填配比具有重要意义。
1.1 基本假定
在进行受力分析时,需对模型进行合理假定,这样不仅可简化计算流程,还能更加符合现场实际情形。本文在LI等[10]和张常光等[17]研究的基础上进行如下基本假定:
1)胶结充填体均为三分层结构,从上到下划分为一、二和三分层,顶部和底部高度相等。
2)一、三分层为假顶和假底结构,其配比完全一致,力学参数完全一致。
3)3个分层内摩擦角相同。
4)不考虑分层胶结充填体与两侧围岩的滑动摩擦效应,假定它们之间只存在黏结滑移效应。
5)分层胶结充填体整体沿一倾斜滑动面发生破坏,滑动面倾角按朗肯主动土压力破坏面确定。
6)后壁非胶结充填体的侧压力为自重应力乘侧压系数:vγuh。其中,v为非胶结充填体的侧压系数,可按公式v=tan2(45-(φ/2))计算[22];γu为非胶结充填体的容重(kN/m3)。
7)充填体抗剪强度(τ)符合莫尔-库仑准则,其表达式为:
τ=C+σtan φ(1)
式中:σ为滑动面法向作用力(MPa);C为充填体内聚力(MPa);φ为充填体内摩擦角(°)。
对图1中各部分力学参数进行设定:h、b和l分别为分层胶结充填体的高度、宽度和长度;p0为分层胶结充填体顶部均布荷载;h1为一、三分层厚度,h2为二分层厚度,hc为坡底距(滑动面坡底距采场底部高度);γ1和C1为胶结充填体一、三分层容重和内聚力;γ2、C2为胶结充填体二分层容重和内聚力;C1′为一、三分层胶结充填体与侧壁围岩的内聚力,C2′为二分层胶结充填体与侧壁围岩的内聚力,且该内聚力通常与胶结充填体内聚力呈一定比例系数,该比例系数受接触面粗糙度的影响,有C1′=r1C1、C2′=r2C2,r1∈[0,1],r2∈[0,1],r1=r2;α为滑动面与水平面的夹角,α=45°+φ/2,因为假定胶结充填体各部分内摩擦角相同,所以滑动面位于同一平面。
参数hc、b及α三者确定了滑动面的位置关系,根据滑动面与各分层面的相交关系,可分为3种情况:第一,滑动面位于第一分层,此时有d=hc+btan α≤h1,d为坡顶距(滑动面坡顶距采场底部高度);第二,滑动面穿过一、二分层,此时有h1≤hc+btan α≤h1+h2;第三,滑动面穿过3个分层,此时有h1+h2≤hc+btan α≤h。
1.2 滑动面位于第一分层
当滑动面完全位于第一分层时,采场结构特征见图2,此时hc+btan α≤h1。
假定两侧围岩粗糙度一致,与胶结充填体黏结作用一致。设楔形滑动体受到两侧围岩的总摩擦力为f,楔形滑动体一、二、三分层受到围岩的摩擦力分别为f1、f2、f3,则有:
1.5 模型验证
不同学者建立的充填体强度模型研究背景不同,因此侧重点和考虑的因素也不相同。将本文模型的安全系数与其他学者的结果进行对比,参数取值见表1,结果见图5。
由图5可知:随中部内聚力和内摩擦角的增大,所有模型安全系数均增大,内聚力增大,膠结充填体细观颗粒之间的黏结强度增加,颗粒抗拉、抗剪能力增大,整体抗破坏能力增大,安全系数增大。内摩擦角增大,等效增大颗粒之间的摩擦系数,颗粒抗剪能力增大,整体抗破坏能力增大,安全系数增大。
其中,张常光等[17]的模型安全系数最大,这是因为其考虑了后壁非胶结充填体对胶结充填体向上的摩擦力,楔形滑动体向上的合力增加,向下发生滑动的趋势减弱,安全系数相应增大;而LI等[10]的模型忽略了后壁非胶结充填体的侧压力,等效于减小楔形滑动体向下的合力,安全系数同样增大;而刘光生[16]的模型认为滑动面坡脚位于采场底部,增大了楔形滑动体向下的合力,因而安全系数相比本文要低一些。
2 分层胶结充填体滑动失稳分析
2.1 滑动面位置确定
通过前面分析可知,滑动面位置由矿房宽度b、坡底距hc和滑动面倾角α三者确定,而α又与胶结充填体内摩擦角相关,因而可根据b、hc和φ三者确定滑动面位置,其他参数取值见表1,结果见图6。
滑动面位置与3个影响因素之间的关系曲线见图6。由图6-a)可知,滑动面坡底距越大,其坡顶距也越大。当矿房宽度较小,坡底距为0~2.0 m时,滑动面始终处于一分层内部;而当矿房宽度增加为8.0 m,坡底距较小时,滑动面位于一分层,坡底距较大时,滑动面会穿过一分层到达二分层;当矿房宽度增大为9.0 m以上时,滑动面位置不再受坡底距影响,始终贯穿一、二分层。由图6-b)可知:滑动面坡顶距随矿房宽度增大而增大,且不论坡底距如何变化,曲线均穿过一、二分层分界线,即当矿房宽度增大到一定程度后,滑动面一定会穿过2个分层,此结论表明,矿房宽度对滑动面位置的影响程度要大于坡底距。由图6-c)、d)可知:胶结充填体内摩擦角对滑动面位置也有较大影响,内摩擦角越大,滑动面坡底距越大。在矿房宽度和坡底距较小时,无论内摩擦角如何变大,滑动面始终位于一分层,而当矿房宽度和坡底距较大时,滑动面会逐渐上移直至穿过2个分层。
综合以上分析,滑动面位置会在一、二分层之间变化,而不太可能会同时穿过3个分层。若滑动面要同时穿过3个分层,其坡底距必须大于底部2个分层高度之和,胶结充填体内摩擦角一般为30°左右,不会有大幅度增加,而滑动面坡底通常位于最底部,即坡底距通常为0,矿房宽度要足够大,此时胶结充填体不符合大高宽比力学模型,其破坏模式也不再是沿滑动面的剪切破坏,上述力学模型已不再适用。
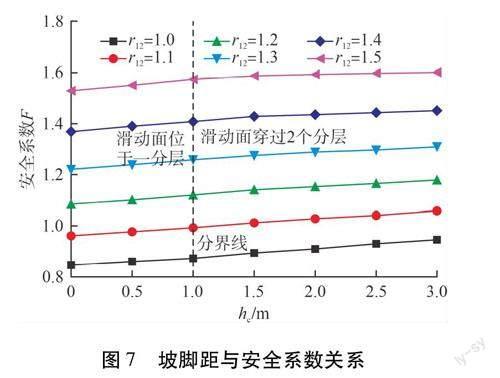
坡脚距与安全系数关系见图7。从图7可以看出,坡脚距对安全系数有一定的影响,当坡脚距较小时(此时滑动面位于一分层),安全系数随坡脚距增大而增大,当坡脚距增大到一定值时(滑动面穿过2个分层),安全系数不再继续增大。且最小安全系数出现在坡脚距为0时,即滑动面与采场底部相交,此时滑动体最不稳定。2.2 安全系数分析
通过前面的分析可知,当楔形滑动体坡脚距为0时,滑动体下滑趋势最明显,滑动体稳定性最差。因此,研究此时滑动体稳定性状况最有意义。采用控制变量法,保持其他变量不变,仅改变单一变量,分析某一变量对滑动体安全系数的影响。其中各因素取值见表1,分析结果见图8~11。
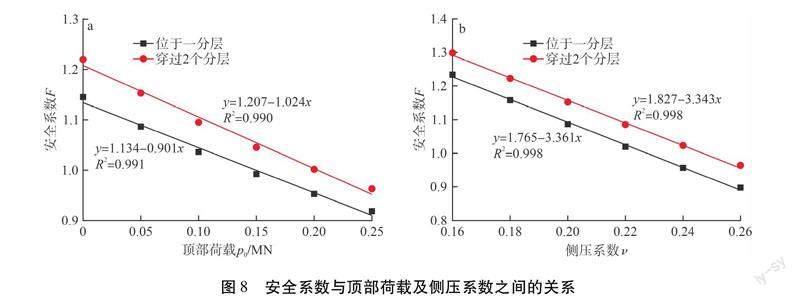
胶结充填体安全系数与顶部荷载及后壁非胶结充填体侧压系数之间的关系见图8。由图8可知:安全系数随顶部荷载及侧压系数增大而降低,且它们之间呈线性函数关系。顶部荷载增加,胶结充填体整体向下的合力增加,导致沿楔形滑动面向下滑移的趋势增加,失稳风险增加,安全系数降低;侧压系数增加,作用在胶结充填体的水平合力增加,楔形滑动体下滑趋势也随之增加,安全系数降低。
安全系数与胶结充填体底部内聚力和中部内聚力之间的关系见图9。由图9可知:安全系数随底部内聚力和中部内聚力的增加而增大,且安全系数与内聚力之间也呈线性函数关系。底部内聚力和中部内聚力增加,胶结充填体内部细观颗粒之间的黏结强度增大,抗失稳破坏能力增大,安全系数增大。
安全系数与胶结充填体底部容重及中部容重之间的关系见图10。由图10可知:安全系数随容重增大而降低,且它们之间也呈线性函数关系。容重增大,楔形滑动体整体质量增大,则其自重力也增大,楔形滑动体整体向下的合力增大,沿滑动面向下的分量也变大,滑动趋势增加,安全系数降低。
胶结充填体安全系数与侧壁围岩内聚力比及胶结充填体内摩擦角之间的关系见图11。由图11可知:安全系数随内聚力比及内摩擦角的增大而增大,它们之间同样呈线性函数关系。内聚力比增大,侧壁围岩对楔形滑动体摩擦力增大,楔形滑动体向上的合力增大,沿滑动面向下的分量减小,滑动趋势减小,安全系数增大;胶结充填体内摩擦角增大,等效增大胶结充填体内部细观颗粒之间的摩擦系数,则整体抗破坏能力随之增大,滑动趋势降低,安全系数则增大。
2.3 影响因素敏感性分析
各参数对巷道位移变化影响程度各不相同,主次顺序各有差异,且由于不同类型参数具有不同的量纲,各参数之间没有共性,很难直接判断影响因素主次顺序。因此,可将这些参数按照一种标准归一化为无量纲区间,然后再进行比较分析。按照式(25)将各参数无量纲化[23]:
式中:E为因素敏感度;Δs为由参数变化引起的巷道位移变化(m);s为某基准参数下巷道位移(m);Δp为参数变化量;p为参数基准值。本文基准值取每个参数区间的最小值。
各参数对安全系数影响程度见图12。由图12可知:胶结充填体底部内聚力对安全系数影响最大,其敏感度高达122 %;顶部荷载对安全系数影响最小,其敏感度仅为20 %。各参数对安全系数影响程度大小依次为:底部内聚力>侧压系数>内聚力比>中部容重>底部容重>内摩擦角>中部内聚力>顶部荷载。
3 讨 论
通过上述分析可知,胶结充填体楔形滑动体沿滑动面破坏类型有3种:滑动面位于第一分层、滑动面穿过2个分层、滑动面穿过3个分层。分别建立了3种破坏类型的安全系数模型,模型计算公式较为复杂,影响因素众多,直接应用于现场交接充填体稳定性计算,存在一定的难度。而通过对滑动面破坏形式的分析可知,其破坏类型主要为前两种,影响因素主要为8种,且各影响因素与安全系数之间均呈现较好的线性函数关系,因此考虑将安全系数计算模型进行简化回归处理,借助SPSS软件,建立安全系数与8种影响因素之间的线性回归方程:
式中:F1和F2分别为第一和第二种破坏类型安全系数计算公式。
回归分析结果见表2,回归结果显示,复相关系数R2均大于0.99,拟合程度较高;标准误差分别为0.007 7和0.008 5,均接近0,说明拟合方程误差非常小;二者显著性F值远小于0.05,表明该回归方程效果显著。
回归方程计算安全系数结果与模型方程安全系数计算结果吻合程度直观度见图13。通过对48个样本数据进行对比分析,可以看到,计算值和预测值高度吻合,发展趋势基本一致,直观上看,回归方程计算结果与模型方程计算结果十分接近。
回归方程计算结果与模型方程计算结果之间的误差范围见图14。由图14可知,2种计算结果误差范围均分布于10 %以内,认为整体误差很小,回归结果十分接近。
为定量分析回归方程计算结果误差大小,引入均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对误差百分比(MAPE)对回归结果进行评估,评价结果见表3。
由表3可知:均方误差(MSE)均远小于0.1、均方根误差(RMSE)均远小于0.2、平均绝对误差(MAE)均远小于0.2、平均绝对误差百分比(MAPE)均远小于15 %,且所有结果平均绝对误差百分比均低于5 %。由此可见,考虑8种因素的影响,采用SPSS软件对安全系数进行多元线性回归分析,回归结果与实际计算结果高度接近,回归模型合理可靠,可直接用于现场胶结充填体稳定性计算分析。
4 结 论
1)针对胶结充填体复杂赋存环境,综合考虑分层效应、后壁非胶结充填体侧压作用、顶部荷载及侧壁围岩摩擦黏结作用,建立了分层胶结充填体滑动失稳模型。根据不同采场结构参数条件,滑动面位置存在3种情形:位于第一分层、穿过2个分层和穿过3个分层。
2)与其他学者的模型对比结果表明,张常光等考虑了后壁非胶结充填体的摩擦作用;LI等忽略了后壁非胶结充填体侧压作用,安全系数较本文更高;而刘光生未考虑滑动面坡脚距,安全系数较本文更低。不同模型研究背景不同,侧重点不同,因而安全系数存在差异,也从侧面验证了本文模型在特定条件下的正确性。
3)胶结充填体安全系数随顶部荷载、侧压系数和容重增大而减小,随内聚力和内聚力比增大而增大,且安全系数与各影响因素之间均呈线性函数关系。各參数对安全系数影响程度大小依次为:底部内聚力>侧压系数>内聚力比>中部容重>底部容重>内摩擦角>中部内聚力>顶部荷载。
[参 考 文 献]
[1]曹帅.胶结充填体结构与动力学特性研究及应用[D].北京:北京科技大学,2017.
[2]汪杰.分层胶结充填体损破演化机理与强度模型研究及应用[D].北京:北京科技大学,2021.
[3]PENG K,LI X B,WAN C C,et al.Safe mining technology of undersea metal mine[J].Transactions of Nonferrous Metals Society of China,2012,22(3):740-746.
[4]张传信.空场嗣后充填采矿方法在黑色金属矿山的应用前景[J].金属矿山,2009(11):257-260.
[5]任卫东,范玉乾.分段空场嗣后充填采矿法集约化开采顺序优化研究[J].金属矿山,2020(6):167-171.
[6]YANG Z Q,ZHAI S H,GAO Q,et al.Stability analysis of large-scale stope using stage subsequent filling mining method in Sijiaying iron mine[J].Journal of Rock Mechanics and Geotechnical Engineering,2015,7(1):87-94.
[7]WANG J,FU J X,SONG W D.Mechanical properties and microstructure of layered cemented paste backfill under triaxial cyclic loading and unloading[J].Construction and Building Materials,2020,257:119540.
[8]汪杰,宋卫东,谭玉叶,等.水平分层胶结充填体损伤本构模型及强度准则[J].岩土力学,2019,40(5):1 731-1 739.
[9]曹帅,薛改利,宋卫东.组合胶结充填体力学特性试验与应用研究[J].采矿与安全工程学报,2019,36(3):601-608.
[10]LI L,AUBERTIN M.A modified solution to assess the required strength of exposed backfill in mine stopes[J].Canadian Geotechnical Journal,2012,49(8):994-1 002.
[11]LI L,MICHEL A.Numerical investigation of the stress state in inclined backfilled stopes[J].International Journal of Geomechanics,2009,9(2):52-62.
[12]LI L.Analytical solution for determining the required strength of a side-exposed mine backfill containing a plug[J].Canadian Geotechnical Journal,2014,51:508-519.
[13]MITCHELL R J,OLSEN R S,SMITH J D.Model studies on cemented tailings used in mine backfill[J].Canadian Geotechnical Journal,1982,19(1):14-28.
[14]ABTIN J,MICHEL A,LI L.Three-dimensional stress state in inclined backfilled stopes obtained from numerical simulations and new closed-form solution[J].Canadian Geotechnical Journal,2018,55:810-828.
[15]劉光生,杨小聪,郭利杰.阶段空场嗣后充填体三维拱应力及强度需求模型[J].煤炭学报,2019,44(5):1 391-1 403.
[16]刘光生.充填体与围岩接触成拱作用机理及强度模型研究[D].北京:北京科技大学,2017.
[17]张常光,蔡明明,祁航,等.考虑充填顺序与后壁黏结力的采场充填计算统一解[J].岩石力学与工程学报,2019,38(2):226-236.
[18]SMITH J D,DE JONGH C L,MITCHELL R J.Large scale model tests to determine backfill strength requirements for pillar recovery at the Black Mountain Mine[C].Proceedings of the international symposium on mining with backfill.Lulea:1983.
[19]LIU G S,LI L,YANG X C,et al.Required strength estimation of a cemented backfill with the front wall exposed and back wall pressured[J].International Journal of Mining and Mineral Engineering,2018,9(1):1-20.
[20]张鹏,高谦,温震江,等.充填体强度影响因素及组合预测模型[J].东北大学学报(自然科学版),2021,42(2):232-241.
[21]尹升华,刘家明,邵亚建,等.全尾砂-粗骨料膏体早期抗压强度影响规律及固化机理[J].中南大学学报(自然科学版),2020,51(2):478-488.
[22]黄亚娟,赵均海,田文秀.基于双剪统一强度理论的刚性结构物竖直土压力计算[J].建筑科学与工程学报,2008,25(1):107-110.
[23]付建新,宋卫东,谭玉叶.岩体力学参数对巷道变形特性的影响程度分析[J].浙江大学学报(工学版),2017,51(12):2 365-2 382.
Stability analysis of cemented tailings backfill in stope considering structural characteristics
Wang Guannan1,Tong Dazhi1,Wang Jie2
(1.Chifeng Shanjin Hongling Nonferrous Mining Co.,Ltd.; 2.School of Civil and Resource Engineering,University of Science and Technology Beijing)
Abstract:In the context of stage-by-stage subsequent backfill mining,this study focuses on the cemented fill body and establishes a safety factor calculation model for large-depth-to-width ratio mining stopes.Based on the Mohr-Coulomb failure criterion and considering the influences of stratification effects,top load,and lateral pressure coefficient,the model takes into account these factors and provides a solution for the safety factor of the cemented fill body.The model is compared and validated against models developed by other researchers,and the influence characteristics of each factor are discussed.The research results show that there are 3 possible locations for the sliding plane: within the first stratification layer,crossing 2 stratification layers,and crossing 3 stratification layers,with the first 2 being the main scenarios.By comparing with other models,the rationality and reliability of the proposed model are confirmed.It should be noted that different models have different research backgrounds and emphases,which may lead to certain differences in the results.The safety factor of the cemented fill body decreases with an increase in top load,lateral pressure coefficient,and unit weight,while it increases with an increase in cohesion,internal friction angle,and cohesion-to-friction ratio.The relationships between these factors and the safety factor are linear.Among them,the safety factor is most sensitive to cohesion and least sensitive to top load.
Keywords:structural characteristics;subsequent backfill;cemented fill body;stratification effect;safety factor;stability analysis
收稿日期:2023-05-30; 修回日期:2023-06-15
基金項目:国家重点研发计划重点专项(2022YFC2905003);中央高校基本科研业务费(FRF-TP-22-113A1)
作者简介:王冠男(1991—),男,工程师,从事金属矿充填开采相关研究工作;E-mail:wangguannan@sd-gold.com
