水工沥青混凝土动态抗压尺寸效应试验研究

2023-09-04杨一帆刘云贺宁致远

水利水运工程学报 2023年4期

董静，杨一帆，刘云贺，孟霄，宁致远

(1. 西安理工大学西北旱区生态水利国家重点实验室，陕西西安 710048； 2. 西安理工大学水利水电学院，陕西西安 710048)

水工沥青混凝土因其优异的防渗性能被广泛应用于沥青面板及心墙土石坝防渗结构，而目前我国已建成或在建的沥青混凝土工程多处于地震频发的西北地区，因此考虑地震工况对工程安全至关重要[1]。针对沥青混凝土在地震作用下的动力特性，国内外学者开展了相关试验研究。Wang 等[2]开展了水工沥青混凝土剪切试验，发现剪切模量等力学参数随应变率增大呈非线性增长；宁致远等[3-4]进行了水工沥青混凝土动态单轴抗压性能试验，结果表明应变率对沥青混凝土动态力学性能及破坏模式具有增强效应，揭示了沥青混凝土弹性模量动态增强因子随应变率增大而提高的变化规律。综上可知，水工沥青混凝土的动态力学性能具有“应变率效应”。然而这些实验室内开展的缩尺模型试验研究大多忽视了试样尺寸对沥青混凝土力学特性及破坏模式的影响。

大量试验研究表明岩石、混凝土等非均质类材料的力学性能具有显著的尺寸效应[5-8]，然而有关水工沥青混凝土力学性能的尺寸效应问题，国内仅有王为标等[9]在早期通过不同尺寸的沥青混凝土弯曲试验进行了初步研究，得出较大尺寸试样变形量大、强度略低的结论。陈宇等[10-11]的研究成果表明温度较低时水工沥青混凝土具有与混凝土、岩石等材料相似的弹脆性力学特征，因此可以借鉴混凝土类材料有关“动态尺寸效应”[12]的研究方法，对沥青混凝土材料在动态荷载作用下的力学性能与破坏模式进行研究。

基于此，本文对不同尺寸的水工沥青混凝土试样开展不同应变率条件下的动态抗压试验，分析研究试样高径比及应变率对抗压强度、弹性模量及破坏模式的影响规律。此外，结合应变率效应及尺寸效应的共同影响，建立不同应变率下水工沥青混凝土动态尺寸效应计算模型。

1 试验研究

本试验中沥青混凝土试样采用现场碾压钻芯成型法获取，具体配合比如下：沥青混合料级配指数为0.4，填料质量分数为13%，沥青质量分数为7%；采用的粗骨料和细骨料均为石灰岩，最大粒径为19 mm，填料（粒径<0.075 mm）为石灰岩矿粉，孔隙率为1.7%~2.1%，密度、针入度等性质均符合《水工沥青混凝土试验规程》（DL/T 5362—2018）[13]要求，沥青混合料级配满足《土石坝沥青混凝土面板和心墙设计规范》（DL/T 5411—2009）[14]规范要求，本文中的沥青混凝土设计级配[13]如式（1）所示：

式中：Pi为筛孔di的通过率（%）；di为筛孔尺寸（mm）；P0.074为di=0.074 mm 时的通过率（%）；Dmax为最大粒径（mm）；n为级配指数，本试验中n= 0.4。沥青混合料骨料级配如表1 所示。

表1 沥青混凝土配合比Tab. 1 Asphalt concrete mixture ratio

现场摊铺碾压并钻取直径为100 mm 的圆柱芯样，切割成高度分别为50、100、150 和200 mm（误差±2 mm）（高径比分别为η=0.5, 1.0, 1.5 和2.0）的试样。其中高度和直径为100 mm（高径比为1.0）的试样为规范[13]中沥青混凝土单轴抗压试验标准试样，本试验中也将其作为其他尺寸的标准对照试样。

采用MTS (Mechanical Testing System)动态疲劳试验系统进行单轴抗压试验。高寒地区沥青心墙经受的最低温度一般为5 ℃[1]，所以试验温度设定为5 ℃。试验过程中通过高低温环境箱实现温度恒定。由于地震作用下混凝土类结构响应的应变率范围为10−4~10−2/s[15]，本试验采用恒定位移速率的加载方式在动态应变率10−4、10−3和10−2/s，准静态应变率10−5/s 的加载条件下进行试验，具体分组见表2。每组进行3 次平行试验，取与平均值误差小于15%的试验数据为有效结果。为降低端部效应对试验结果的影响，加载前对切割成型后的试样端面进行打磨，试样端面及加载端板处涂抹硅油。

表2 动态抗压尺寸效应试验方案Tab. 2 Test scheme of dynamic compression size effect

2 试验结果及分析

2.1 破坏模式

高径比为1.0 时，试样在不同应变率条件下的破坏模式如图1 所示。应变率为10−5/s 时，试样表面只有骨料脱黏产生的较小裂缝但无贯通裂缝，破坏模式是以沥青基质被挤出、骨料与基质脱黏等现象为主的黏结破坏；随着应变率的增大，试样表面出现了沥青基质断裂、挤出，粗骨料压碎，骨料竖向断裂等现象，且脱黏裂缝与骨料裂缝逐渐连接贯通，最终在试样表面呈现出贯通斜裂缝，即斜剪破坏。上述现象表明随着应变率增大，试样的破坏程度逐渐增强，破坏模式由黏结破坏逐渐向斜剪破坏发展。Tekalur 等[16]的研究中也表明了该结论。

图1 不同应变率下高径比为1.0 试样的破坏模式Fig. 1 Failure mode of specimens with the height to diameter ratio of 1.0 under different strain rates

应变率为10−3/s 时不同高度试样的破坏模式如图2 所示。当高径比为0.5 时，部分骨料被压裂，且有部分骨料被挤出，试样表面有明显斜裂缝，斜裂缝在垂直方向贯穿试件。当高径比为1.0 或1.5 时，试样表面的斜裂缝显著减少。沥青混凝土的非均质性导致裂缝分布存在随机性，斜裂缝分布在试件中部或其上下区域附近，但仍主要集中在试件中部，且试件在荷载作用下表现出明显的剪胀性。剪胀可以认为是沥青-骨料接触面剪切过程中产生的摩擦势能突破法向应力的束缚而产生能量释放的过程[17]，出现剪胀是由于沥青混凝土骨料在沥青基质界面互相咬合、位错，界面粗糙度较高，试样内储存较高的摩擦势能。当高径比为2.0 时，骨料无明显破坏，试样无贯通裂缝，脱黏破坏少量分散在试件中部，破坏模式为沥青基质与骨料脱黏而产生的黏结破坏，且随着高径比增加，试样相对高度增加，而摩擦势能基本不变，导致剪胀现象变得不明显，破坏程度降低。

图2 10−3 /s 应变率下不同高径比试样的破坏模式Fig. 2 Failure patterns of samples at different height to diameter ratios under 10−3 /s strain rate

在相同加载速率条件下，当高径比增大时，试样的破坏程度降低，破坏模式由斜剪破坏逐渐转变为黏结破坏。高径比增大时裂缝产生和发展或者试件变形的空间越多，但应力波传递速度基本不变，裂纹有足够的时间沿阻力最小的路径扩展；随着高径比增大微裂纹发展需要更多的能量，但相同应变率下输入能量基本不变，导致贯穿试件的主裂纹转变为骨料-沥青界面的界面裂纹，这也是破坏模式由斜剪破坏变为黏结破坏的原因。

图1 和2 的试样破坏特征表明，沥青混凝土试样的破坏模式受到应变率效应及尺寸效应的影响，应变率对试样的破坏程度具有增强效应，而试样高径比则对其破坏程度具有减弱效应。当应变率为10−5/s 时，图3 中不同尺寸试样的破坏特征表明，各尺寸试样破坏形式均以骨料脱黏、基质挤出为主，仅有少量斜裂缝出现，试样破坏程度随高径比的变化远不如应变率为10−3/s 时显著，这是由于高应变率下试样应力可认为是静态应力与动态“惯性力”的叠加[18]，破坏程度敏感性更高。结合其他工况下的试样破坏模式（限于篇幅未给出全部图片）可知，应变率越大，试样破坏程度随高径比增大而减弱的趋势越明显。

2.2 动态抗压力学参数

本试验取沥青混凝土应力-应变曲线中50%抗压强度点与10%抗压强度点之间的连线斜率为弹性模量[13]，得到不同高径比沥青混凝土试样的动态抗压强度及动态弹性模量平均值如图4 所示。

图4 各应变率下各尺寸试样力学参数试验值与理论值Fig. 4 Experimental and theoretical values of samples with various sizes under different strain rates

由图4 可见：沥青混凝土抗压强度随高径比增大呈非线性降低，随应变率增大而增大，当试样高径比由0.5 增大至2.0，应变率为10−5/s 时，抗压强度由5.01 MPa 降至2.30 MPa，降幅54.1%；应变率为10−2/s 时，抗压强度由35.98 MPa 降至15.59 MPa，降幅56.7%。而随高径比增大及应变率增大，弹性模量则呈非线性增强，当试样高径比由0.5 增大至2.0，应变率为10−2/s 时，弹性模量由0.51 GPa 增至1.59 GPa，增幅211.76%；应变率为10−5/s 时，弹性模量由5.08 GPa 增至12.71 GPa，增幅150.20%。结合破坏模式可发现随着高径比增加，抗压强度降低、弹性模量增高，即试样承受的峰值压应力变小，同时抵抗变形的能力增强，导致破坏程度随之降低，剪胀程度减弱。这是由于当高径比增大时，沥青混凝土材料内部出现局部缺陷的可能性越大，且材料在各向上更不均衡，导致抗压强度降低。上述数据表明，沥青混凝土抗压强度及弹性模量受高径比与应变率影响显著。

“三个一”精准化钻井实现了技术措施监控由事后处理向事前控制的转变。以往井队做出技术决策后对公司技术部门存在不报或瞒报问题，只有技术措施执行不下去或出现复杂故障的时候才向技术部门汇报。对此公司技术部门采取以下措施：

3 动态抗压尺寸效应计算模型

3.1 尺寸效应

国内外学者在类混凝土材料的尺寸效应研究方面取得了丰富的研究成果[19-21]，低温条件下沥青混凝土具有与类混凝土材料相似的力学特性[10-11]。因此为描述沥青混凝土试样的抗压强度、弹性模量随试样尺寸的非线性变化关系，本研究在类混凝土材料尺寸效应理论[6]的基础上进行修正。Bažant 尺寸效应理论采用式（2）进行描述：

式中：σ0为混凝土名义强度；D为特征尺寸；B、D0为经验系数；ft为混凝土拉伸强度。根据式（1）通过等量纲参数替换，将特征尺寸取为高径比，抗压强度扩展至弹性模量等力学参数，B、D0取为与高径比相关的经验系数βc与ηc。由此可得：

式中：Fc为沥青混凝土试样的力学参数（抗压强度、弹性模量）；η为圆柱形试样的高径比；Fc,100为标准试样（高径比为1 时）的试验力学参数；βc与ηc为对应不同Fc的拟合参数。

图5 为各试验条件下沥青混凝土抗压强度、弹性模量的试验值及通过式（3）计算得到的理论曲线，拟合参数见表3。基于文献[22]引入抗压动态增强因子fCDIF(Compressive Dynamic Increase Factor)，以此反映在不同应变率下水工沥青混凝土力学性能的变化规律。其中抗压强度动态增强因子表示为fCDIF(σ)，抗压模量动态增强因子表示为fCDIF(E)。由图5 可知，各试验值均在拟合曲线附近，与试验结果吻合较好，可见式（3）能够较好地描述各应变速下水工沥青混凝土力学性能的尺寸依赖性。

图5 不同尺寸沥青混凝土fCDIF 随应变率的变化趋势回归曲线Fig. 5 Regression curve of fCDIF with strain rate for different sizes asphalt concrete

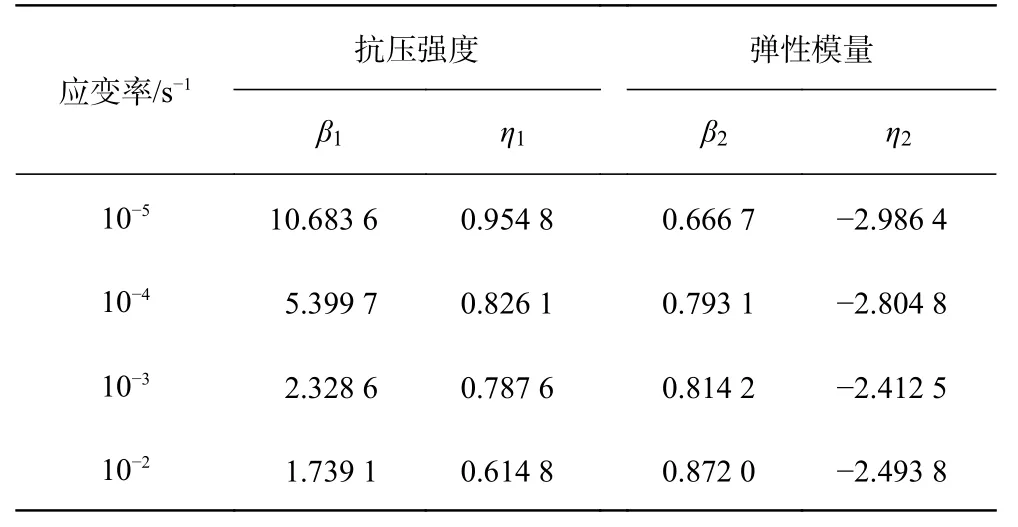
表3 不同应变率下 β 、η 的拟合参数Tab. 3 Fitting parameters of β and η at different strain rates

3.2 应变率效应

上述试验结果分析表明沥青混凝土动态力学性能表现出显著的应变率效应，同时应变率的变化对力学性能的尺寸效应规律也具有明显的影响作用。fCDIF(Fc)定义为动态应变率条件下的各项抗压力学性能数值与其在应变率为10−5/s 条件下的数值之比，采用Logistic 函数形式对其进行拟合分析：

式中：Fc代表各尺寸试样的力学参数；Pd、Ps分别为动态及准静态加载条件下的力学参数；表示动态应变率(10−4/s，10−3/s，10−2/s)；表示准静态应变率10−5/s；α为材料参数。则抗压强度fCDIF(σ)、弹性模量fCDIF(E)与应变率的回归关系如下：

不同应变率条件下抗压强度、弹性模量的抗压动态增强因子拟合曲线见图5，拟合参数α及相关系数R2见表4。可见，式(5)、(6)对试验值的拟合效果良好，能较好反映不同应变率下动态抗压强度及动态弹性模量随应变率的增长特性，这是由于应变率较大时，试样无足够时间用于变形及能量积累，通过增加应力的途径来提供能量，从而抗压强度和弹性模量表现为明显增长。应变率越大，抗压强度、弹性模量具有的应变率增强效应越显著。

表4 不同尺寸试样对应的α 参数Tab. 4 α parameter corresponding to different height samples

3.3 动态抗压尺寸效应计算模型

如前文所述，试样力学性能与高径比的关系随应变率的变化而明显变化，即应变率影响沥青混凝土抗压性能的尺寸效应规律。而式（3）无法表征力学性能尺寸效应的应变率敏感性，因此在应变率效应分析的基础上引入应变率影响因子 φε˙。在单轴抗压试验中，应变率影响因子取抗压动态增强因子：φε˙=fCDIF，对式（3）进行修正得到式（7）：

将式（3）代入式（7）得：

由式（8）得到抗压强度随高径比和应变率变化的主曲面，如式（9）、图6 所示。

图6 沥青混凝土动态抗压强度理论值与试验值对比Fig. 6 Theoretical and experimental values of dynamic compressive strength of asphalt concrete

同理，沥青混凝土弹性模量随高径比和应变率变化的主曲面，如式（10）、图7 所示：

图7 沥青混凝土动态弹性模量理论值与试验值对比Fig. 7 Theoretical and experimental values of dynamic elastic modulus of asphalt concrete

拟合曲面反映的抗压强度及弹性模量变化规律与试验结果一致。由图6、7 可知，由于试验数据点数量不够充足且公式无法考虑试验中影响力学参数的所有因素，故部分拟合值与试验值略有偏差，但试验结果均分布于拟合曲面上或附近，且拟合数值误差大多在20%以内，虽然个别数值误差偏大，但其力学参数变化规律仍然具有较高的一致性（见表5），拟合效果良好，可认为误差在合理范围内。