结合极化自注意力机制的空间目标位姿估计

2023-09-04窦凯云樊永生

航天控制 2023年4期

窦凯云,樊永生,王涛

1.中北大学大数据学院,太原 030051 2.中北大学电气与控制工程学院,太原 030051

0 引言

近年来,人类太空活动日渐频繁,在轨航天器数量与日俱增。传统航天器造价昂贵却只能一次性使用,因而在轨服务出现,为太空中的航天器提供部件维修、更换等服务[1]。通过目标飞行器相对于服务飞行器的位姿估计推断目标的运动状态,是空间在轨服务的基础和关键技术之一。位姿估计是估计相机坐标系下目标的位置和姿态。传统的目标位姿估计方法包括基于特征点的方法、基于模板的方法和基于点云的方法,整体是通过从图像中提取特征后建立二维像素点与三维位置点的对应关系来计算位姿[2]。基于特征的方法是通过提取图像像素中的局部特征与三维模型上的特征进行匹配,建立2D-3D对应(典型的如PnP算法),从而得到位姿信息。它对于物体之间的遮挡有很好的处理效果,但需要丰富的纹理来计算局部特征。基于模板的方法是通过模板匹配得到物体的位姿信息,对无纹理对象效果很好,但对光照和遮挡都很敏感。基于点云的方法处理对象是点云数据,通过求解3D-3D特征点的对应关系来获取位姿,对光照敏感,因此不适用于室外场景。

随着近年来深度学习的发展,通过卷积神经网络[3]从图像中学习目标的位姿特征提高了目标位姿估计的速度和准确度[4]。Yu等[5]提出的PoseCNN网络可以从RGB图像中直接回归得到6D相机姿态,其将VGG网络提取的图像特征输入到分割、平移、旋转3个网络分支。其中,分割分支得到每个像素的类别标签;平移分支通过投票机制估计位置信息;旋转分支在RoI Pooling后通过全连接层回归到四元数得到目标的姿态信息。Do等[6]提出的Deep-6D pose框架同样采取了直接回归的方式,与PoseCNN不同,它的位置分支与姿态分支全部使用全连接层直接回归的方式,并且创新性的采取了李代数表示旋转信息。除了直接回归以外,Rad等[7]提出的BB8将CNN网络获取的物体三维边界的顶点投影到二维图像中,通过PnP算法计算位姿。Pix2Pose[8]和PVnet[9]等方法同样是获取图像的关键点后建立2D-3D映射关系,通过PnP方法得到6D位姿。

相比采用关键点进行预测,使用PnP算法计算位姿,直接回归能够以端对端的方式输出位姿。本文与直接回归的位姿估计方法如Deep-6D pose相比,引入Polarized Self-Attention注意力机制嵌入到残差网络ResNet-50[10]中,利用其独特的极化滤波和HDR机制,对图像中空间目标的空间信息通过加权进行了增强,提高姿态估计的精准度。同时借鉴PoseCNN的方法解耦位姿,用2个分支分别获取图像的位置和姿态信息,但不同于PoseCNN。PoseCNN使用2个分支用于姿态回归,1个用于位置回归。在姿态信息回归分支上,对姿态信息进行软分配编码,相比于直接回归能有效减少姿态误差。最后在URSO数据集上进行了实验验证,实现了空间目标的端对端位姿估计。

1 网络结构设计

空间目标的位姿估计包括位置估计和姿态估计,本文采用端对端的回归法从图像数据中学习空间目标的位姿映射关系以得到位姿数据。

1.1 网络框架

对于给定的输入图像,姿态估计的任务是获取目标从物体坐标系到相机坐标系的变换,包括三维平移和三维旋转。由于两者有着不同的度量单位,分别为米和度,因此解耦为2个网络分支分别计算。如图1所示,整体网络包括3个阶段:

图1 网络结构图

1)主干网络。用残差网络ResNet-50提取图像的深层特征。由于空间目标位姿估计需要深度学习网络具备较强的空间位置提取能力,将Polarized Self-Attention注意力机制模块嵌入残差块中,利用其独特的极化滤波和HDR机制,对图像中空间目标的显著特征信息通过加权进行了增强。

2)嵌入网络。将主干网络输出的二维特征图输入到可调节通道数的3×3卷积核进行二维卷积,步长为2,从而降低输出维度,进行降维卷积处理,最终将特征图经过拉平成一维数组,为后面全连接层的运算极大地减少了参数量,从而降低了训练时间。

3)分支网络。通过前两阶段生成的图像特征通过2个分支分别输出位置信息和姿态信息。其中,采取了两层全连接层结构以直接回归方式输出三维信息。第一个全连接层用于将拉平后的特征图信息再进行降维操作,压缩至1024个维度,经过ReLU激活函数后,再将该层输出数据输入到下一个全连接层,最终输出为三维数据,直接对应所求的三维坐标信息x,y和z。

姿态分支基于软分配编码实现,输出四元数的姿态信息[11]。其中的核心思想是将姿态四元数按照高斯分布模型进行编码,转换为姿态离散空间中的概率质量函数值,因此该分支结构针对概率质量函数进行学习。最终可将网络输出的包含概率质量函数的三维矩阵解码,得到估计出的位姿四元数值。

1.2 注意力机制

在空间目标的位姿估计中,空间位置提取能力对结果精准度有很大影响。对于包含空间目标的整张图像,空间目标只占其中有限的一部分,其余的是太空背景和地球背景,占据了不小的面积。在深度学习过程中,这些背景信息由于参与了卷积等计算,产生了冗余信息,对空间目标的识别、定位和位姿估计均产生了干扰。因此,在深度学习过程中,针对性地提高空间信息的权重,降低不必要的干扰至关重要。为了实现空间目标的精准位姿估计,减少背景信息的干扰,本文将PSA(Polarized Self-Attention)注意力机制模块嵌入到残差块中以解决该问题。

Polarized Self-Attention[12]由南京理工大学和卡内基梅隆大学于2021年联合提出,是一种基于像素级回归的双注意力机制。它有2个特点:

1)极化滤波:大多数的像素级回归为了鲁棒性和计算效率而输出低分辨率的特征,高度非线性的物体边缘部分会因此损失很多分辨率特征。而Proenca等[13]的研究表明,位姿估计对图像分辨率的敏感度很高。PSA的极化滤波机制是使一个维度的特征完全折叠,其正交方向的维度保持高分辨率。如通道维度特征折叠,则空间维度特征保持高分辨率。因此,对于空间目标的位姿估计的精准度有一定的帮助。

2)High Dynamic Range(HDR):对注意力模块中最小的特征张量进行softmax归一化以扩宽注意力范围,进行信息增强,然后使用sigmoid函数进行投影映射。

PSA注意力模块分为通道分支和空间分支,在计算完成后通过串联进行融合。

PSA注意力模块中通道分支的权重计算公式为:

Ach(X)=FSG[Wz|θ1(Wv(X))×FSM(σ2(Wq(X)))]

(1)

其中:Ach(X)∈RC×q×1,FSM表示softmax函数,FSG表示sigmoid函数,W表示不同的卷积操作,σ表示不同的降维操作,×表示矩阵点积运算。

通道分支先通过卷积操作Wv把通道数压缩为一半,然后将其由二维特征图降为一维,与压缩全部通道的空间特征信息点积后,通过卷积Wz恢复通道数,最后经Sigmoid归一化,把不同通道的权重加权到原来的特征上。另外,压缩全部通道的空间信息还通过FSM函数进行了一次信息增强。

空间分支的权重计算公式为:

Asp(X)=FSG[σ3(FSM(σ1(FGP(Wq(X))))×

σ2(Wv(X)))]

(2)

其中:Asp(X)∈R1×H×W,Wv和Wq为卷积操作,σ1和σ2为降维操作,σ3为升维操作,FSG、FSM、FGP分别为sigmoid函数、softmax函数和全局池化。

空间分支与通道分支不同之处有2点:1)压缩全部空间的通道信息,经过了卷积、全局池化、降维和softmax函数回归;2)点积后没有再一次的卷积操作,而是直接通过σ3恢复维度。

可见,PSA同时在空间和通道维度上保持了高分辨率,并且利用softmax对瓶颈张量进行了非线性激活。调整权重,即赋予重要特征信息更大权重,有助于增强图像空间通道的显著特征,更精准地定位空间目标在图像中的位置。

因此,本节在主干网络ResNet-50的残差块的BN层前加入PSA注意力机制模块,使网络更好地注意到图像中空间目标的空间信息,同时尽可能减少图像复杂背景的干扰。

1.3 软分配编码

姿态信息进行软分配编码[13]:首先为每个姿态角划分24个区间,进而可以得到13824个姿态信息离散点,并可以近似地一一对应空间中任意一个姿态旋转矩阵,用集合Q={b1,…,bN}来表示。其中,bi为用四元数形式表示的第i个姿态。然后对每个姿态信息bi按照下式进行软分配编码:

(3)

其中:K(x,y)为核函数,利用归一化的姿态轴角偏差表示2个四元数x和y之间的相对误差为:

(4)

(5)

其中:方差σ2表示量化误差;Δ/M表示量化步骤;Δ为平滑项;M为三个姿态角各自划分的区间数目。

对网络输出的概率质量函数进行解码,即可得到估计的位姿四元数。网络输出的概率质量函数可用集合{w1,…,wN}表示。然后估计出的四元数为:

(6)

其中:N为姿态离散空间的离散点数目。

另外,在回归的过程中,使用如下的损失函数来保证四元数的归一化:

(7)

如图1中右下的姿态分支网络结构所示。同样的,姿态分类分支与位置回归分支的第1层结构仍然大体相同,为全连接层,区别在于第2全连接层之后的部分。第2层所输出的维度为M×M×M维的,经过ReLU激活函数以及softmax分类,从而得到估计出的M×M×M维概率质量函数矩阵,到此网络完成训练部分。接下来是解码该矩阵,进而得到输出的四元数姿态信息。

1.4 损失函数

由于位置分支和姿态分支采取不同的回归方法,因此采取不同的损失函数。

位置分支使用相对误差形式而不是欧式距离。这是由于空间目标数据集的z轴范围是10 m到20 m,当目标的z轴距离偏大时,导致欧式距离即估计位置与实际位置的几何距离非常大,从而在小批量训练中加大了对远距离目标图像学习的位置损失函数的权重,最终使网络对近距离目标位置的估计能力下降。位置损失函数定义如下:

(8)

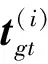
姿态信息的损失函数可由标签信息编码后的正态分布离散函数值与输出信息的概率质量分布的交叉熵计算得到,交叉熵计算如下:

(9)

其中:x为离散空间中的一个四元数,Q={x1,…,xM3}为在离散空间上的四元数集合,p(x)为网络对x的概率质量函数值,q(x)为由标签值编码后的概率质量函数对x的值。

2 实验验证

2.1 数据集

用于空间目标的识别、定位和位姿估计等的URSO数据集[13]基于虚幻引擎4(Unreal Engine 4)构建,用于渲染绕地球运行的航天器的高清图像。USRO数据集是从近地球轨道高度在地球上随机取5000个视点,空间目标随机在摄像机观察范围10～20 m之间。其中,地球的自转、相机方法和空间目标的姿态都是随机生成的。数据集分为训练集、测试集和验证集,后两者分别使用5000张图像中的10%,图像的分辨率大小为1280×960。图2为部分展示。

图2 URSO数据集(部分)

2.2 评价指标

评价指标是用来反映模型潜在的问题和评价模型性能优劣的定量指标。常规的是对各类物体位姿估计,本文是对一类物体即空间目标估计,因此采用欧空局针对空间目标提出的一套位姿估计评价方法[14],分别计算位置和姿态误差。

位置误差的计算公式如下:

(10)

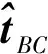
姿态误差的计算公式如下:

(11)

空间目标图像的位姿估计的总误差即为位置误差和姿态误差的总和,所有空间目标位姿估计的平均位姿误差为总和除以图像数量。

2.3 实验结果

URSO数据集中包含复杂的太空背景和地球背景,有些航天器被淹没在地球背景中。本文提出的空间目标深度学习位姿估计,即使在复杂的地球背景下仍能够获得鲁棒的估计结果。基于URSO数据集测试本文算法,数据训练180次,前100次学习率为0.001,后80次为0.0001。在相机坐标系下,根据2.2节评价指标,测试集的位置误差为0.85 m,姿态误差为9.7°。如图3和图4所示,随着迭代次数增加,位置和姿态误差趋于稳定。

图3 位置迭代误差图

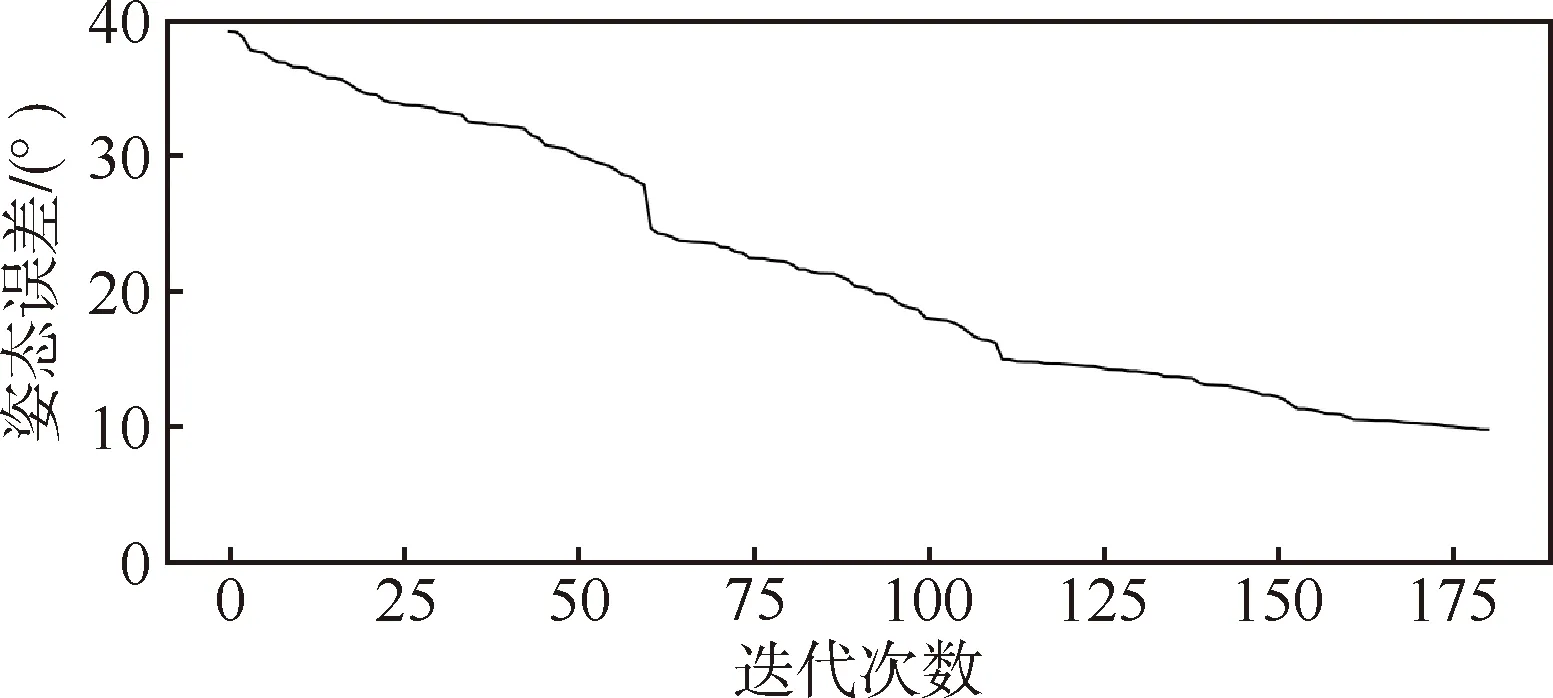
图4 姿态迭代误差图

图5给出了利用USRO数据集对本算法进行测试的可视化结果。在空间目标图像中,为了进行可视化,将姿态信息的四元转换为方向余弦矩阵后,结合相机参数映射到空间目标图像中,红、蓝、绿三个箭头分别表示航天器的俯仰角、滚转角和偏航角,而三个箭头的交汇处即为空间目标的位置。

图5 基于URSO数据集的测试结果

图5中的空间目标图像在对小数点后3位四舍五入后,实际位置信息和姿态信息分别为[-0.601,3.455,17.287]和[0.147,0.408,0.452,0.779],而估计值分别为[-0.723,3.163,16.051]和[0.134,0.379,0.476,0.782],根据2.2提出的评价指标计算误差,位置信息的平均绝对误差约为0.95 m,姿态信息的角度误差约为4.53°。其中,图5(a)为位置可视化图,两个斑点分别表示真实位置和预测位置。图5(b)展示了姿态信息在欧拉角的极坐标图形式下的预测误差,两条虚线分别表示真实和预测角度信息。图5(c)为姿态直观可视化图像。由此可见,本文所提算法具有一定的精准度。

为了验证PSA注意力机制对于空间目标图像位姿估计精度提升的有效性,在URSO数据集上进行了消融实验,如表1所示。分析表1结果,对比可见,引入Polarized Self-Attention注意力机制可使得图像位姿估计位置误差精度从1.1 m提升到0.85 m,姿态误差精度从10.9°提升到9.7°,表明引入注意力机制可以增加算法对图像中重要特征信息的筛选能力,通过权重提升有效增强了算法在空间上的特征表达能力,有效提升了模型的估计精度。