基于双电极传感器的腐蚀电流检测系统抗扰技术
2023-09-04岑远遥刘聪万军贺琼瑶何建新周俊
岑远遥,刘聪,万军,贺琼瑶,何建新,周俊
(西南技术工程研究所,重庆 400039)
金属腐蚀对装备的结构具有较大的破坏性,且金属腐蚀的破坏性是缓慢持续的过程,在短期内,金属腐蚀不会对装备造成较大的影响,但长时间会造成装备结构损伤。近年来,随着海洋装备的大力发展,在这背后面临着一个重要的挑战,就是装备金属结构的腐蚀[1-4]。海洋装备常服役于海洋环境中,装备内部不易检测的结构常发生腐蚀现象,在腐蚀后不能被及时发现并采取有效的补救措施,极大地影响了装备的技战术性能,严重的可能造成装备服役寿命缩减,造成巨大的经济损失[5-7]。
金属材料的腐蚀往往不能消除,只能进行提前有效的预防,因此针对复杂自然环境下金属腐蚀以发现、检测为目的的腐蚀检测技术就显得至关重要,尤其是在不易检查的关重结构位置[8-9]。早期腐蚀检测的重要性表现在2方面:一方面,装备定期的拆装检查不仅消耗大量的人力、物力,而且可能会影响整体性能,造成不必要的损失;另一方面,当用肉眼可以观察到腐蚀效果时,其腐蚀厚度已经达到金属原始厚度的10%,此时就需要花费大量的人力和财力进行修复。
当前,常用的腐蚀检测方法有传统的金属挂片法、电化学方法、光纤光栅传感器等方法。其中,金属挂片法不能长期实时地检测数据,需要人工测量;电化学方法则是通过测量金属电流、电阻等参数来表征金属腐蚀等级;光纤光栅传感器稳定性好,但光纤光栅信号解调复杂,不宜实现便携式和狭小的装备内部环境中的原位监测。为实现实时监测腐蚀情况,在线监测中主要的方法有[10-12]电偶腐蚀电池法、电化学阻抗谱、薄膜电阻传感器、石英晶体微天平、电化学噪声监测等方法,这些方法均需要利用高精度信号采集实现。
彭旺林[13]为了提高微弱电流信号检测的信噪比,针对运算放大器的电流偏置与失调电压对前置放大电路采样精度的影响,提出了基于多目标遗传算法优化的线性约束自适应噪声抵消方法,并采用三参数的最小二乘拟合的代数方程算法对数据进行了修正,修正后的数据平均增长率约降低52%,平均误差为1.368%。王选择等[14]利用二分程控法消失调电压的微电流测量方法,完成了0.1 μA电流的采集。李辉等[15]针对系统噪声与电路板布局布线对电流检测精度的影响,利用低偏置高精度运放结合Guarding环保护与屏蔽电缆归环技术,实现了分辨率优于1 pA的电流检测。叶磊[16]研究了放大电路的相位超前相位补偿,实现了pA级至μA级电流的采集。
经过实验测试,双电极传感器发生腐蚀后,会产生100 pA~10 mA的电流。通过腐蚀持续过程中腐蚀电流大小的实时检测,利用腐蚀电流的大小则可以表征金属腐蚀速率,而在微弱电流的采集中受电流采样方式、电路噪声等的影响较大。
本文对双电极传感器腐蚀电流检测技术进行了研究。首先,对电流检测系统总体方案进行设计,确定出I-V转换方式,对运放偏置产生的影响,拟选择fA级偏置电流的运放进行跨阻放大,对采集系统的噪声问题通过设计自适应滤波器对噪声进行抑制,通过MATLAB进行仿真分析,验证了自适应滤波器在微弱电流采集中的有效性。
1 系统总体方案研究
检测系统的整体原理如图1所示。检测系统主要由双电极探头、I-V转换电路、信号调理电路、电源系统、高精度数据转换电路、STM32控制器、温湿度传感器等构成。
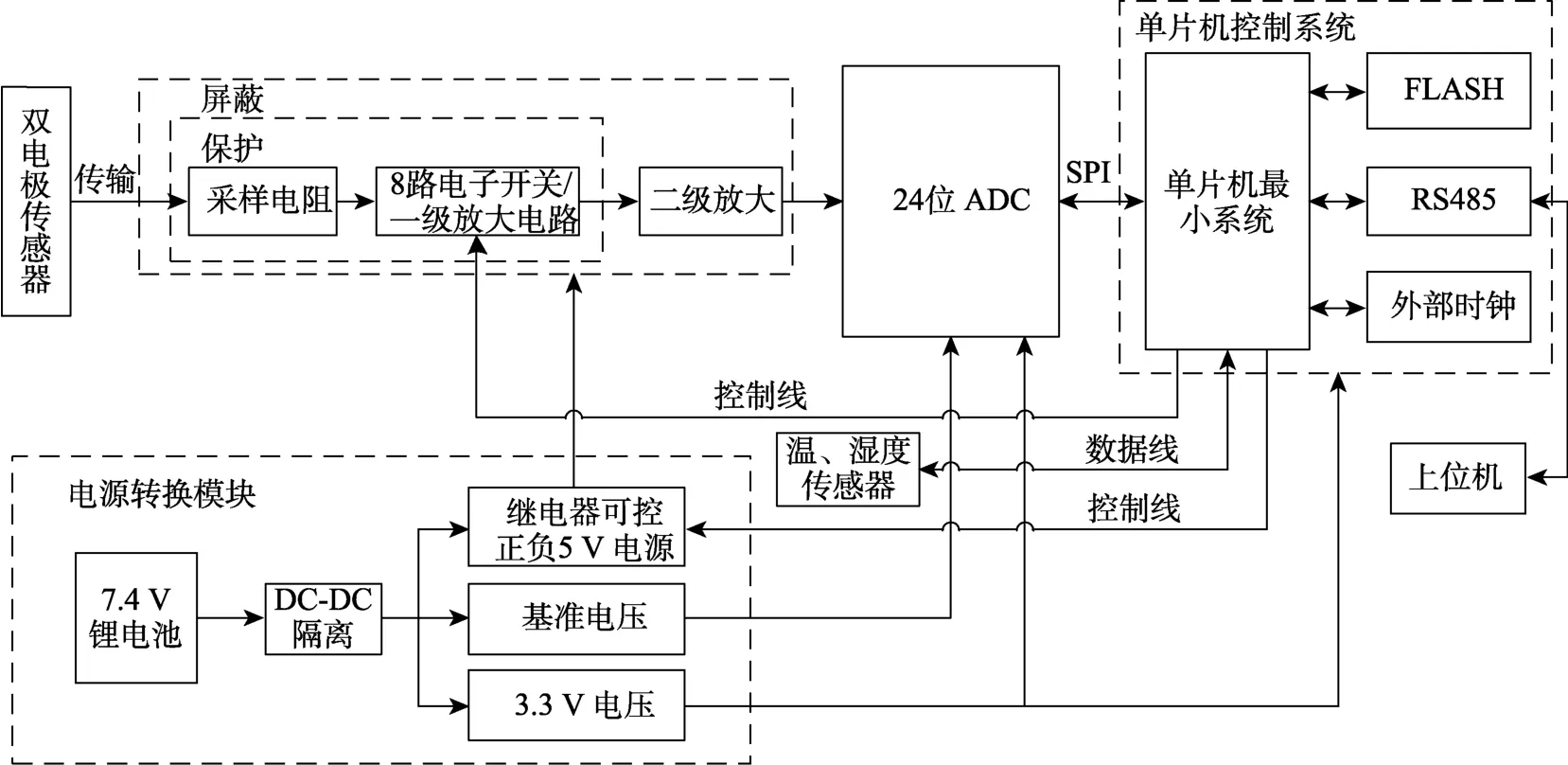
图1 腐蚀电流检测系统总体设计Fig.1 General design of corrosion current detection system
1.1 微弱电流调理方案研究
在微弱电流的信号采集中,电流的取样方式较为重要,常采用的方法主要有采样电阻法、反馈积分法、反馈电阻法等方式[14-16]。不同采样方式的采样结果完全不同,为此对采样方法展开研究。
1.1.1 采样电阻法
取样电阻法进行的I-V转换如图2所示。此方法结构简单,通过1个电阻即可实现I-V转换,但会使Is变大,因为V0=IsR,只要Is增大,V0就会增大。Is不是理想电流源,则很难全部流进R,腐蚀电流较小,一般为nA级,这样会导致测量误差增大[17-18]。
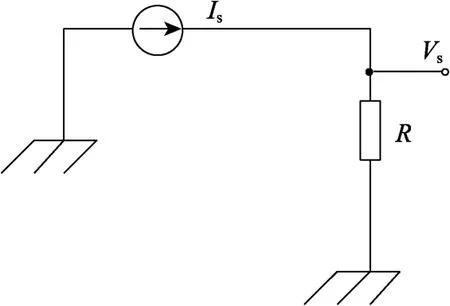
图2 采样电阻法Fig.2 Sampling resistance method
1.1.2 反馈积分法
反馈积分法如图3所示。反馈积分法的原理是通过I-F转换后,通过电流Is对电容Cf进行充电,积分法在一定的时间内对电容进行积分可以降低因为模拟电路带来的噪声影响,但积分会影响整个测量系统的响应时间。

图3 反馈积分法Fig.3 Feedback integral method
式(1)为系统在理想状态下,通过积分输出的电压变化量表达式:
其中:Is为输入电流;Cf为积分电容;T1、T2为积分时间。
随着积分时间的累积,电容的电荷量ΔQ不断增加,电荷量可用式(2)进行表示。
通过积分时间与电荷量之间的关系则可以计算出此时间内的平均电流Iavg。
在实际的使用中,运放存在偏置电流Ib和输入失调电压Vos,当考虑相应的偏置电流和失调电压的影响后,则电压可以表示为式(4)。
在本方案中,若采用电容积分法,采样电路受偏置电流和失调电压的影响,设计时选择低偏置电流和失调电压的运放降低其影响,可实现较高精度的电流测量。但因需要对电容进行长时间积分,会增加整个系统的功耗,不利于系统长时间、户外的随装检测,会造成系统的工作时间变短,因此不宜采用I-F转换方案设计。
1.1.3 反馈电阻法
反馈电阻法如图4所示。此方法是利用运放的“虚短”特性进行测量,在理想运放下,Is可以全部进入反馈电阻Rf,在输出端Vs转换为正确的值[19]。此方法与反馈积分法一样会受到偏置电流和偏置电压的影响,输入偏置电流Ib和信号Is将会同时流过反馈电阻Rf,可以得出采集电流输出的真实值,如式(5)所示。
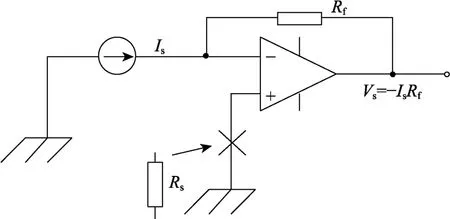
图4 反馈电阻法Fig.4 Feedback resistance method
其中:Rs为电流源内阻。
由此可以得到因为运放特性带来的误差,见式(6)。
电流源的内阻因可认为是无穷大的,所以式(6)可以简化为式(7)。
此种方法测量电流虽然存在一定的误差,但是相较前2种测量方法更具有优势,此方法不需要对电容进行积分,所以在不需要对电流进行采集的时间可以使系统保持低功耗模式,可以增加系统的工作时间。对偏置电压带来的影响则可选择低偏置运放,同时可以设计调节电路与软件滤波器滤波的方式对运放的输出进行调节,提高系统的采样精度。
1.2 信号调理技术研究
1.2.1 运放型号分析确定
跨阻放大器的测量误差来源于输入偏置电流和偏置电压,虽然可以通过硬件设计的方法消除一定程度的偏置电压的影响[20],但仍需要选择输入偏置电流和偏置电压较低的运放。随着集成电路的飞速发展,目前集成运放的偏置电流已经可以达到fA级,偏置电压在μV级,同时还要保证运放的输入电阻Ri尽可能地大,才可以保证电流尽可能地经过反馈电阻Rf,输出结果更接近理论值[21]。对于测量电流最小为100 pA,若跨阻放大器输出10 mV电压,则需要使用Rf=100 MΩ。若选择偏置电流为1 nA的运放,则经过100 MΩ反馈电阻后,输出电压也达到100 mV,是不合理的,因此需要偏置电流更小地运放。若保证偏置电压输出小于100 μA以下,则需要保证运放偏置电流低于1 pA。
通过上述的理论分析,本设计的运算放大器选择应满足如下条件[22]:运算放大器的输入偏置电流Ib应低于1 pA;运算放大器的失调电压Vos要尽可能小;运算放大器的输入电阻Ri的阻值应该充分大,输入电流尽可能流入反馈电阻,即输入电阻应当远大于反馈电阻,不小于100 TΩ。
通过综合对比分析后,选择ADA4530-1型运放进行设计,其主要参数见表1。

表1 ADA4530-1型运放主要性能参数(25 ℃、典型值)Tab.1 Main performance parameters of ADA4530-1 operational amplifier (25 ℃, typical value)
该型运放具有极低的偏置电流和温度系数,对环境温度的影响具有更大的容错性。同时ADA4530-1具有较好的噪声水平,在0.1 Hz时,电流噪声密度仅0.07 fA·Hz1/2,极低的噪声电流降低了因电流噪声过大反馈电阻而产生的误差。
1.2.2 采集系统档位调节方案
经实验室研究后发现,本次设计的双电极传感器在发生腐蚀时会产生100 pA~10 mA的微弱电流。对于宽范围的电流,采用跨阻放大器进行I-V转换后,无法使用1个采样电阻实现8个数量级电流的转换,因此设计基于ADG708电子开关的8路量程切换档位,档位与采样电阻对应关系见表2。档位调节电路设计原理如图5所示,通过单片机即实现对电子开关通道进行切换,从而实现不同档位电阻的采样。
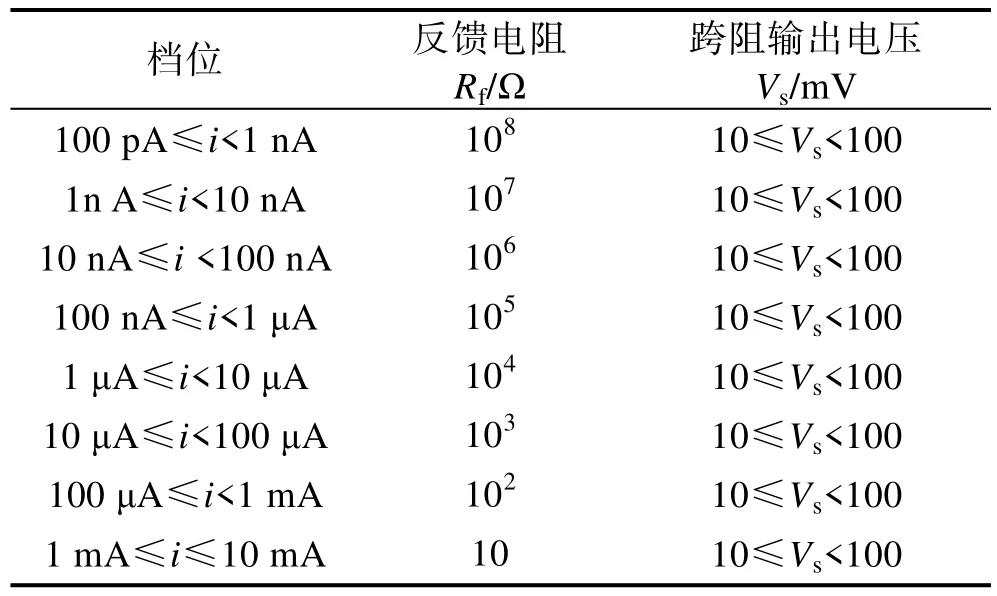
表2 系统调节档位Tab.2 System adjustment gear
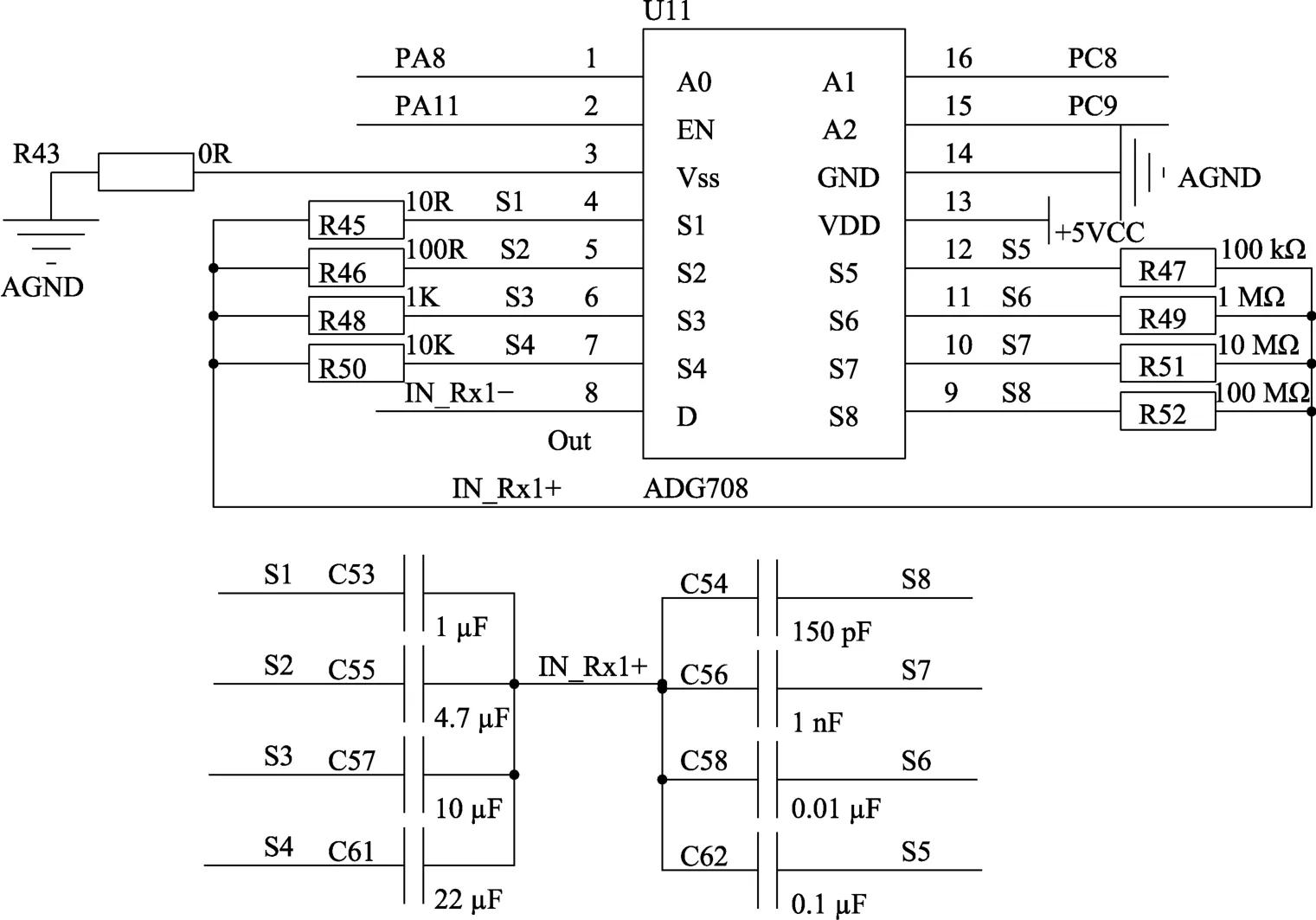
图5 档位调节电路设计Fig.5 Design of gear adjustment circuit
1.2.3 采集系统调理电路设计
设计的采集系统调理电路如图6所示。调理电路由ADA4530-1型运放组成跨阻放大器,LMC6001运放实现的是第二级放大,设置增益为25倍。通过R55后,ADC检测到的电压范围则是250 mV~2.5 V,ADC选择的是24位Σ-Δ型模数转换芯片,有效分辨率可达23位。
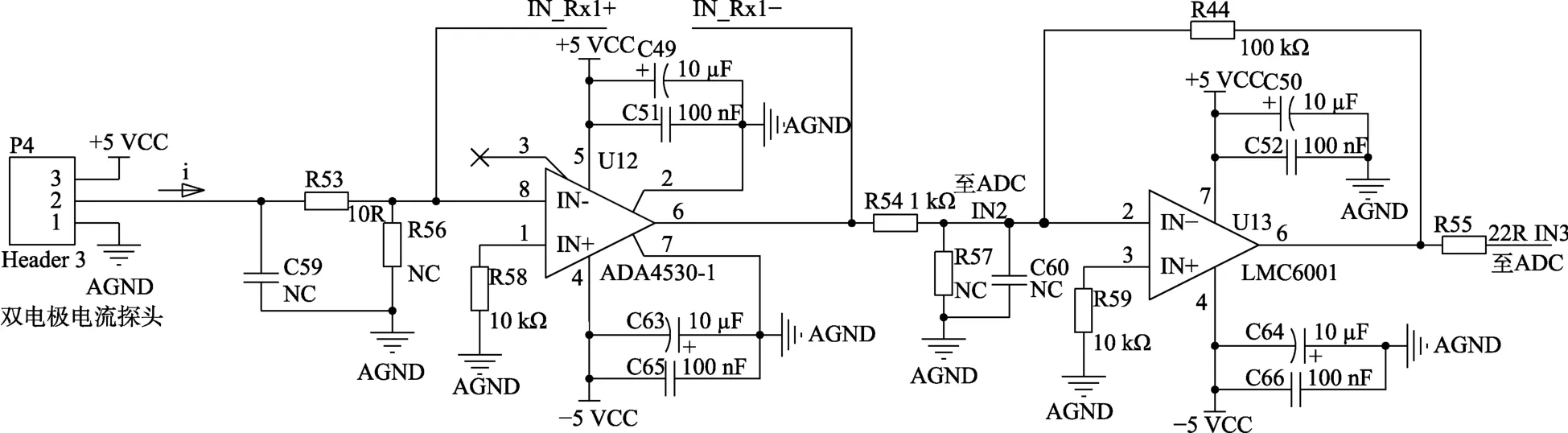
图6 I-V转换调理电路原理设计Fig.6 Principle design of I-V conversion conditioning circuit
通过式(8)可计算出双电极传感器输出电流i。
式中:K为模数转换后的数字量;A为第二级运放放大倍数,A=25;Rf为采样电阻,共8档。
1.3 系统软件控制原理设计
系统软件的控制原理如图7所示。为实现低功耗长期户外随装检测,系统未采用实时数据采集,通过设计时间阈值(可调)t=10 min,检测电流值。检测时,按档位8→档位1的顺序检测,当读取到的电压转换值在10 mV≤Vs<100 mV时,则保存数据,数据保存完后,进入下一次循环。
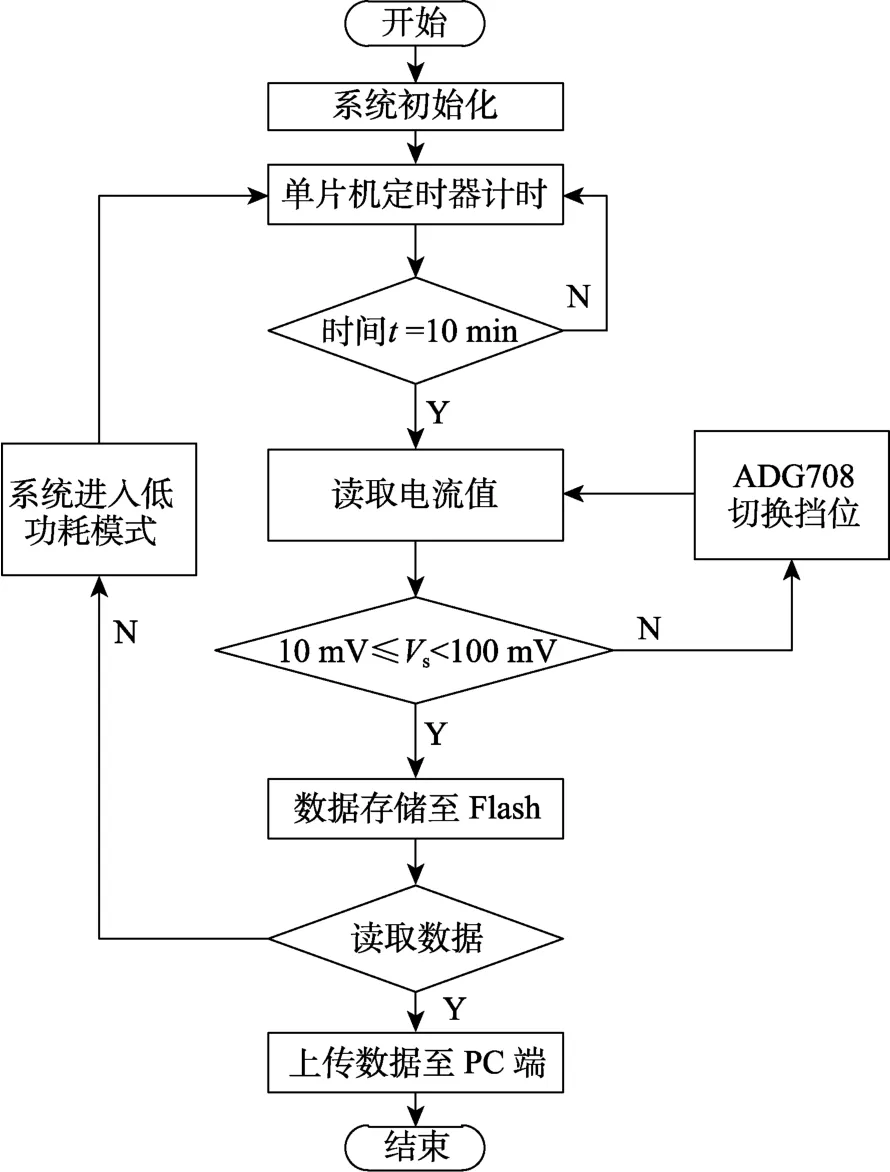
图7 软件原理设计框Fig.7 Block diagram of software principle design
1.4 双电极传感器设计与制作
双电极传感器与腐蚀挂片方法测得结果具有很好的线性相关性[23],设计的双电极传感器检测探头如图8所示。传感器探头A极采用的是铝制作,C极采用铜制作,按照ACAC……的顺序进行组合。各5片同种材料之间采用导线进行连接,中间采用0.3 mm厚的聚乙烯薄膜制作。传感器除测试表面外,其余表面均采用环氧树脂进行密封。
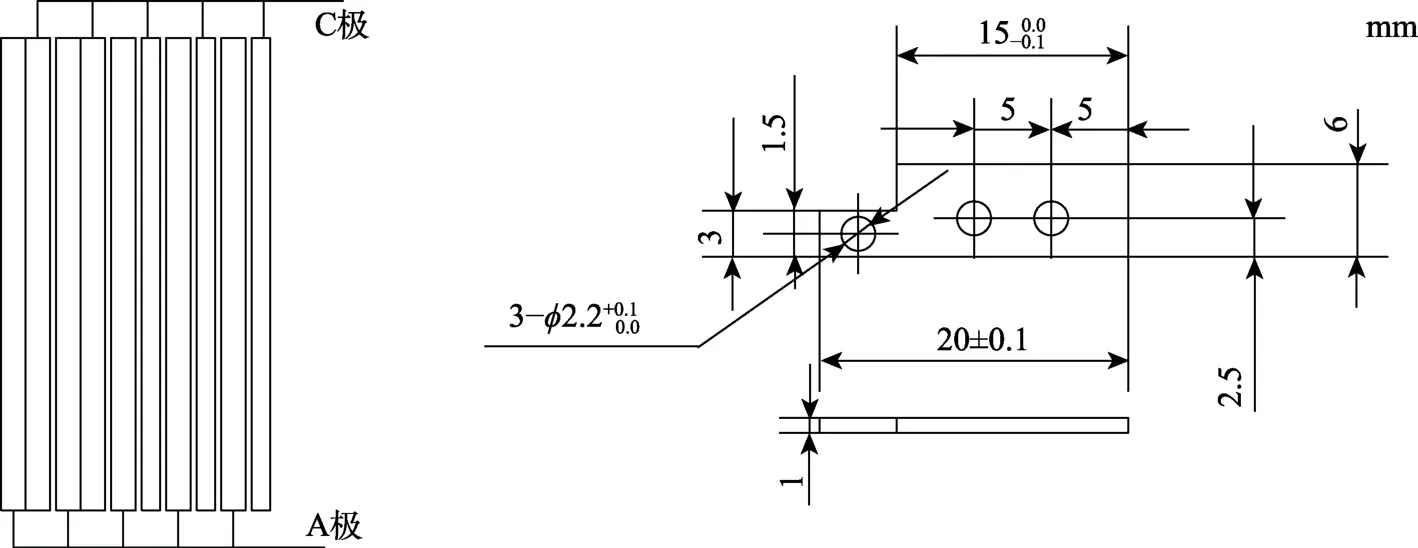
图8 双电极传感器尺寸结构Fig.8 Dimension block diagram of double-electrode sensor
2 系统抗扰技术研究
微弱电流信号调理通过I-V转换后,转换为可测的电压信号,解决了“微”的问题,而在pA级电流或nA级电流的检测中,弱电流信号可能被噪声淹没,关键则是抑制噪声提高信噪比突破“弱”的问题[24]。在微弱电流跨阻放大中,部分档位阻值较大,因为大阻值反馈设计与分布电容易形成RC低通滤波器,导致完整通过的信号频率降低。在工程应用中,针对电路噪声问题,常采用设计滤波算法抑制系统噪声,提取有用信号。
2.1 自适应滤波器设计
自适应滤波器(LMS)和维纳滤波器类似,均是在某种准则下的最佳滤波器,但维纳滤波器的输入信号是平稳的,这就需要对原始输入信号有一定的先验知识[25]。自适应滤波器降低了对输入信号的要求,使得滤波器的特性随着信号和噪声的变化而变化,即使输入信号的规律发生变化,自适应滤波器通过自身调整也可以达到最佳[26]。自适应滤波器结构如图9所示。
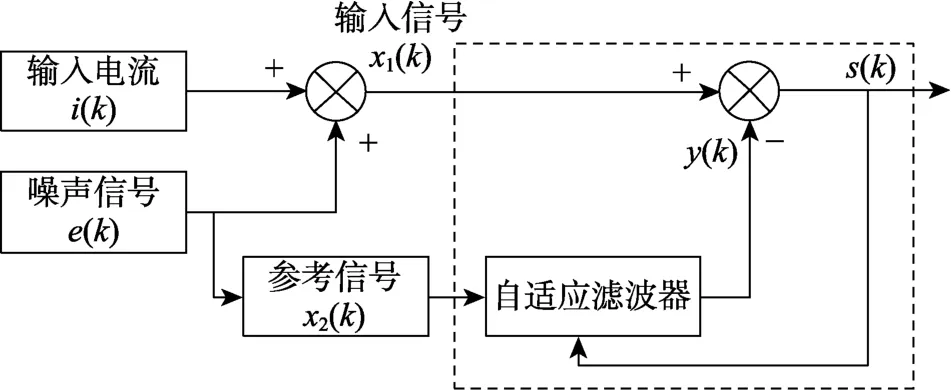
图9 闭环自适应滤波器原理Fig.9 Principle of closed-loop adaptive filter
输入信号x1(k)是带有噪声的电流信号,由噪声不相关的信号源i(k)和噪声e(k)构成,即有:
参考信号是与i(k)不相关但与e(k)相关的信号,参考信号经过自适应滤波器处理后,产生的信号为y(k),可以表示为:
式中:M为自适应滤波器阶数;wn为k时刻的第n个可调滤波器系数(抽头权值)。输入信号x1(k)与y(k)信号之间的差值为误差值s(k),有:
将误差信号s(k)用于自适应滤波器的滤波系数,同时该误差信号是整个系统的输出,即滤波后的信号,系统的噪声分量可以表示为e(k)-y(k)。自适应滤波器的目的就是将e(k)-y(k)降到最小,在最大程度上保留原始无噪声信号,消除输入信号中的噪声,最后输出s(k),即腐蚀电流。
2.2 自适应滤波算法
自适应滤波算法是系统在达到“某一最佳准则”下,系统的滤波效果可以达到最佳。目前常用的滤波算法主要有:最小均方误差准则、最小二乘准则、最大似然等方法[27]。通过对比3种滤波算法,最小均方误差准则具有简单高效、鲁棒性强的优势,因此设计该算法用于电流检测滤波。自适应滤波器在k时刻的向量定义如下。
滤波器抽头系数向量W(k)为:
输入向量为:
自适应滤波算法流程如图10所示。
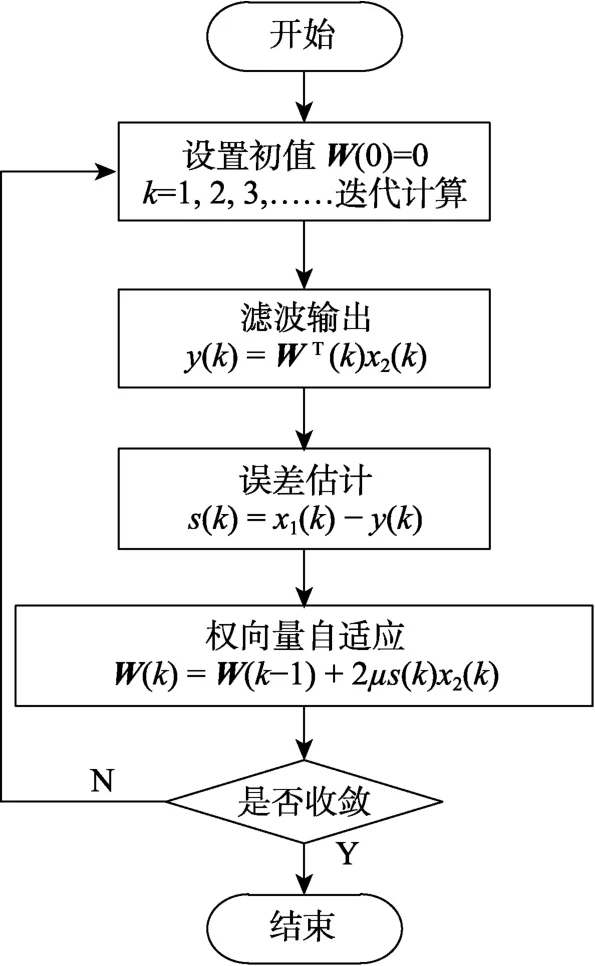
图10 自适应滤波算法迭代流程Fig.10 Iterative flow of adaptive filtering algorithm
2.3 自适应滤波器仿真
在MATLAB中构建电流采样仿真环境,为模拟采样过程中产生的噪声,自适应滤波器的噪声信号为白噪声,输入电流信号的幅值为2 mA,相位为0,频率ω=1 Hz,即i(k)=2sin(2πk)。经过多次仿真后,确定出滤波器阶数M=5,采用滤波步长的最优值。无LMS控制下,输出信号与理论值对比如图11所示,通过数据统计后可以得到数据误差为0.29 mA(1σ);LMS控制下,输出信号与理论值对比如图12所示;LMS控制下输出信号的误差如图13所示,经统计后得到误差为0.003 9 mA(1σ)。仿真结果表明,引入LMS控制后,系统的采样精度得到有效提升,验证了LMS控制对提高微弱电流采样精度的有效性。
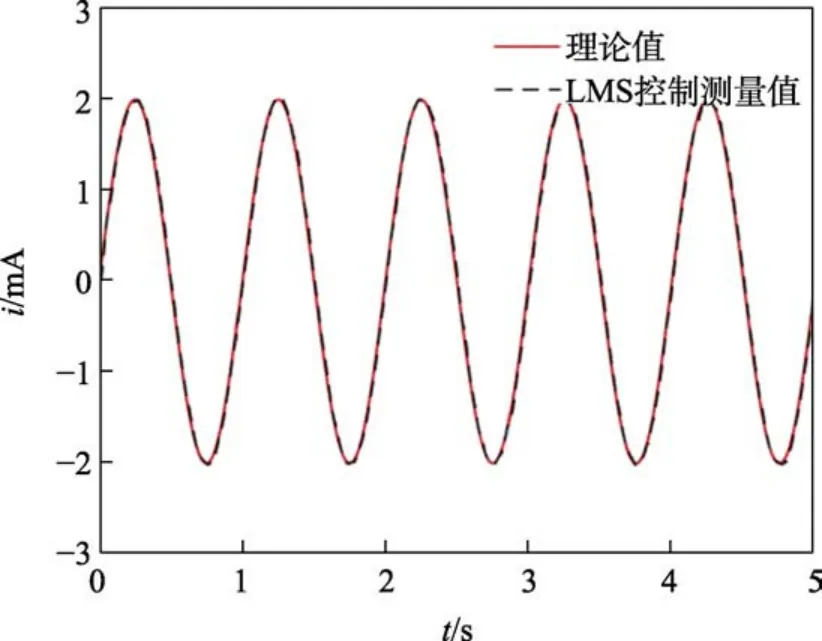
图12 LMS控制下正弦波电流信号采集Fig.12 Sine wave current signal acquisition under LMS control
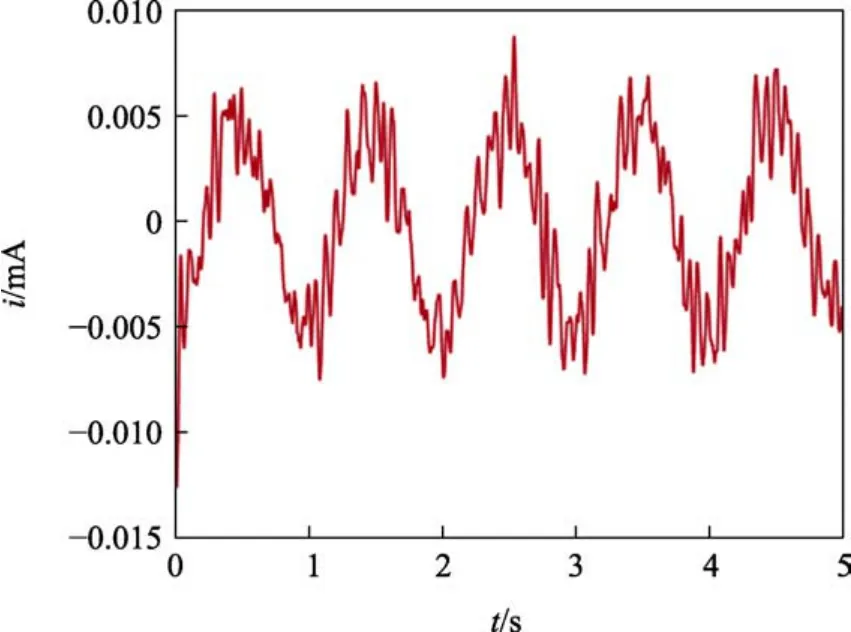
图13 LMS控制下电流信号采集误差Fig.13 Current signal acquisition error under LMS control
3 实验验证
3.1 测量系统精度测试
在系统完成标定后,采用恒流源输出,将输出接口接在采集模块的输入接口上[28],每采样点测试3次,取平均值,然后计算出相应的误差,实验室进行的电流精度测试数据如图14所示。在100 pA时,误差最大,为4.7%;在10 mA测量时,误差最小,为0.049%。

图14 实验室电流监测精度测试Fig.14 Laboratory current monitoring accuracy test
通过上述测试数据表明,在输入电流大于100 nA时,测试误差可在1%以内。当测试精度低于1 nA时,测试误差在5%以内。表明该课题所研究的微弱电流测试系统的检测精度较高,可应用在双电极传感器腐蚀电流检测中。
3.2 双电极传感器测试
在完成滤波器设计与系统精度测试后,构建如图15所示的测试系统,对双电极传感器的数据进行测试,测试时间为2022年9月10日—2022年9月21日,共12 d,采样频率为1/600 Hz(即10 min采集一次数据)。江津站棚下的测试数据如图16所示。

图15 微弱电流测试系统搭建Fig.15 Construction of weak current test system
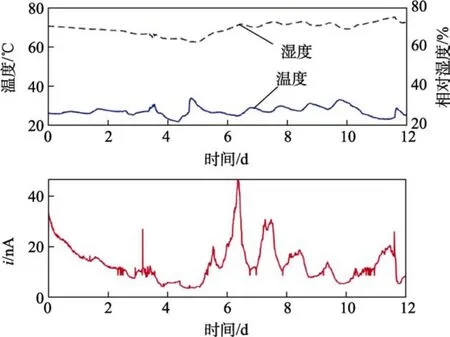
图16 江津站实测数据Fig.16 Measured data of Jiangjin Station
4 结论
本文针对腐蚀电流检测设计了一种高精度宽范围微弱电流检测系统。
1)借助理论分析方法,结合微弱电流调理方法,通过对比采样电阻法、反馈积分法和反馈电阻法等方法,设计了基于ADA4530-1的跨阻放大电路实现微弱电流的I-V转换。
2)借助MATLAB仿真分析,对设计的自适应滤波器进行仿真。仿真结果表明,在LMS控制下系统的误差从0.29 mA(1σ)降低至0.003 9 mA(1σ),系统精度提高了2个数量级,表明自适应滤波在微弱电流采集中的有效性。
3)实测结果表明,检测电流在100 nA以下,系统的误差在5%以内;检测电流在100 nA以上,系统误差在1%以内。
4)研究成果能够用于装备随装检测金属腐蚀速率,实现装备腐蚀实时检测。
