内流激发垂直悬臂管振动失稳特性实验研究

2023-09-04罗航周顶昌马永奇冯爱春

装备环境工程 2023年8期

罗航，周顶昌，马永奇，冯爱春

（1.驻武汉地区某军事代表室，武汉 430064；2.上海交通大学船舶海洋与建筑工程学院，上海 200240）

垂直悬臂管是深海采矿、海洋热能转换（OTEC）、油气管道和核热转换装置等诸多工业装备的重要组成部件[1-4]。当管道内部流速较低时，管道振动很小，一般忽略不计。当管道内部流速较大时，会使管道与内流耦合系统的阻尼变为0，管道呈现强烈的振动失稳现象。该现象会降低管道的输运效率，造成疲劳破坏，危害管道的作业安全。陶立佳等[5]、Paidoussis等[6-8]和Ma等[9-10]已对此问题做了大量研究。

Kuiper等[11]利用欧拉-伯努利梁理论模型研究了吸水悬臂管的振动特性，研究发现，管道在超过临界流速的内流作用下会失去稳定性，管道振幅明显。该现象亦得到实验结果证实。Giacobbi等[12]、Rinaldi等[13-14]分别以气流为实验流体，发现吸气管在相对较低的流速下也会出现颤振失稳运动。Ge等[15]开发了一套研究流固耦合颤振不稳定性的实验设施，实验结果表明，随着管道长度的增加，临界流速具有渐近特性。谢孝文[16]提出了细长输流曲管边界条件的一种通用处理方法，通过约束刚度来控制边界条件，发现输流管道固有频率随着约束刚度值的增加而增大。许锋等[17]研究了弹性支承输流管道在均布载荷作用下的失稳特性，结果表明，支承刚度对临界流速有较大的影响，支承刚度和均布载荷的大小会影响输流管道失稳类型。易浩然等[18]通过实验研究了附加重块对悬臂管稳定性和振动模态特性的影响，发现附加重块布置位置对输流管振幅和模态的影响显著。袁嘉瑞等[19]建立了基于Timoshenko梁理论的微曲输流管道横向振动动力学模型，分析了内流作用下微曲管道的横向振动特征，发现内流流速以及管道的弯曲幅度对管道横向振动频率均有显著影响。刘颖等[20]研究了外界激励力对悬臂管失稳特性的影响，数值结果表明，激励力位置对一阶振动幅值的影响显著。曹建华等[21]推导了旋转悬臂管的线性振动微分方程，分析发现，随着管道转速的增加，临界流速增大，临界流速曲线的稳定区域也随之增大。

现有文献对内流作用下的管道振动特性进行了深入的研究，但很少对内流和外部流体共同作用下的垂直悬臂管失稳特性进行研究。在海洋油气和深海矿产资源装备中用于液体输运的垂直悬臂管，受到内流和外部流体的共同作用。因此，本文利用实验方法研究了垂直悬臂管失稳振动的位移时程、振幅、时频特性、相位变迁和振动频率，多角度分析管道的失稳振动特性同内流流速和浸没深度之间的内在关系。

1 试验

为研究内流激发垂直悬臂管的振动失稳特性，搭建了一套封闭循环的输水系统，该系统可采集管道在不同内流流速和浸没深度时的振动位移时程，根据位移时程数据，分析其振动失稳特性。

1.1 试验装置

该试验装置位于上海交通大学水声工程水池，水池的尺寸为5 m×5 m×5 m，主要由以下几个系统组成：试验水池、封闭管道循环系统、输运动力系统、流速测量系统和振动位移捕捉系统，每个系统的具体部件如图1所示。系统采用水作为试验介质进行循环。试验管道自由端入水口位于水池底部上方1.5 m处，以保证入水口附近的流场不受水箱底部的影响。位移传感器系统安装在距离管道顶部1.25 m处，以250 Hz采样频率记录管道振动位移时程。电磁流量计以50 Hz采样频率测量管道系统内的内流流速。

图1 垂直悬臂管内流激振试验装置Fig.1 Experimental apparatus for cantilevered pipe induced by flow

内流由离心泵驱动，通过调频器控制离心泵的转速来生成不同的内流流速。通过调节水池内液面高度来控制试验管道的浸没深度。在试验研究中，采用12个不同的内流流速U，流速间隔由调频器控制，每5 Hz为一间隔，内流流速值由电磁流量计采集得到。定义管道浸没深度h与管道长度L之比为无量纲浸没深度系数ι，即ι=h/L。试验采用8个不同浸没深度（0.05、0.10、0.175、0.25、0.35、0.425、0.5、0.6）工况。

1.2 试验管道

为实现水池空间的最大化利用，试验管道长度选为4 m。试验管道分别选用50 mm和63 mm 2种外径，这2种管道可通过螺纹与试验设施管路系统紧密连接。管道材料为PVC，该材料一方面具有较好的强度，可保证管道在大幅振动中不会疲劳断裂。另一方面具有良好的刚度，产生的振动现象较为明显，适合试验记录和分析。管道1、2的主要几何和物理特性见表1。

表1 管道主要的几何和物理特性Tab.1 Main geometric and physical properties of pipe

1.3 试验步骤

试验管道安装前，需要利用拉力试验机校核管道的弹性模型。在试验开始前，需确保整个系统各部件紧密连接，管道表面无开裂，管道内部无堵塞。本试验按照以下步骤有序完成，

1）设定管道浸没深度ι=0.05，管道内流流速U=0，给管道自由端一初始位移并释放，利用无接触激光位移传感器记录管道振动的位移时程，待管道静止时停止测量。

2）改变调频器的频率来提高离心泵的转速，内流流速从0逐渐增加到设定速度，观察电磁流量计读数，待流速保持恒定3 min后，利用激光位移传感器记录管道振动的位移时程。

3）数据采集3 min后，停止测量。重复步骤2），测量下一个流速，直到流速达到设定的最大值，测量结束后，关闭输运动力系统和位移捕捉系统。

4）调节试验水池的液面深度，使悬臂管达到指定的浸没深度，重复上述步骤，完成试验设定的88个管道浸没深度工况。

每个试验工况重复进行3次，以3次试验的平均值作为试验结果进行分析，以减小试验误差。

2 结果分析与讨论

通过垂直悬臂管试验重点研究了内流流速和管道浸没深度对管道振动特性的影响。利用管道的振动时间历程、临界流速、振动振幅、时频、相位和频率等参数来研究不同流速和浸没深度影响下管道的振动失稳现象，以揭示内流激发悬臂管道的振动特性及其与内流流速和浸没深度间的内在关系。

2.1 管道振动频率和位移时程

管道1和2的自然频率和振动频率与浸没深度的变化关系如图2所示，此时内流流速U=0。管道1和2的自然频率分别为0.55、0.81 Hz，随着浸没深度的增加，管道在水中的振动频率明显减小。这是因为随着浸没深度的增加，外部流体对管道的黏性阻力增加，导致管道的振动频率减小。管道的振动频率同浸没深度基本呈现线性关系，管道1和2的振动频率随管道浸没深度变化可分别拟合为下列线性关系：

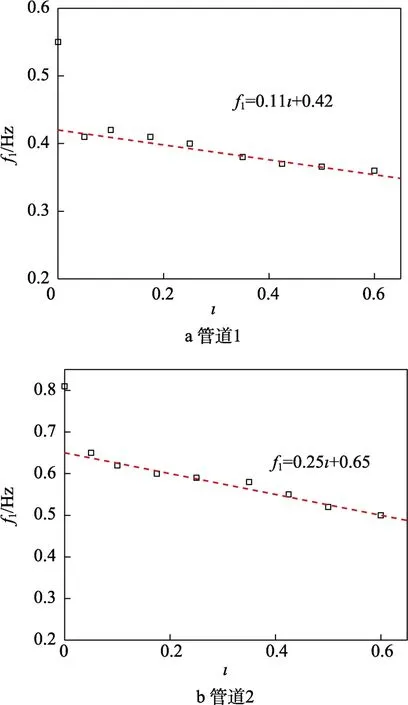
图2 管道1和管道2的自然频率以及振动频率随浸没深度的变化Fig.2 Natural frequency and vibration frequency of pipe 1 and pipe 2 with various submersion depth: a) pipe 1; b) pipe 2

其中F1为振动频率。拟合优度分别为0.934 9、0.970 3，拟合结果较好。由式（1）、（2）可以看出，管道2的振动频率随着浸没深度的变化速率要大于管道1，即管道2的振动频率对浸没深度较管道1更为敏感，这是由于管道2的刚度EI和浸没面积均大于管道1。

内流流速U=3.2 m/s和浸没水深为ι=0.05时管道的位移时程曲线如图3所示。从图3可观察到，管道在前20 s小振幅抖动之后发生颤振，振幅突然增加，持续到60 s后又回到小振幅抖动的状态。因此，振动呈现小振幅的抖动与大振幅的颤振交替发生的特征。Kuiper等[11]、Giacobbi等[12]和Rinaldi等[14]在其文献中也报道了类似的试验现象。

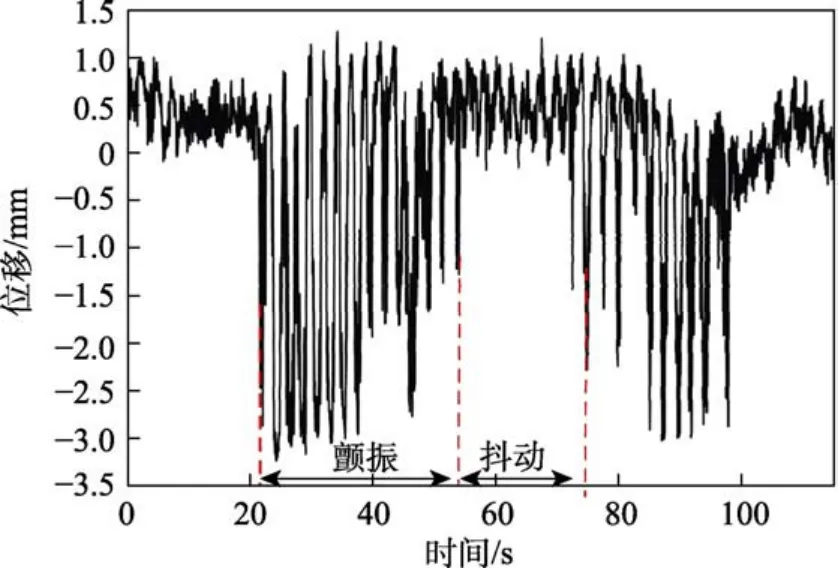
图3 流速U=3.2 m/s和浸没水深为ι=0.05时管道的振动时间历程Fig.3 Displacement of pipe measured by the displacement transducer for flow velocity U=3.2 m/s and submersion depth ι=0.05

2.2 管道振幅

管道振动的均方根（Root Mean Square，RMS）振幅可表征振动振幅的统计特性。管道的RMS振幅随内流流速U的变化情况如图4所示，通过线性拟合可得临界流速Ucr的数值。从图4可以看出，内流激振管道振动响应可分为3个状态：

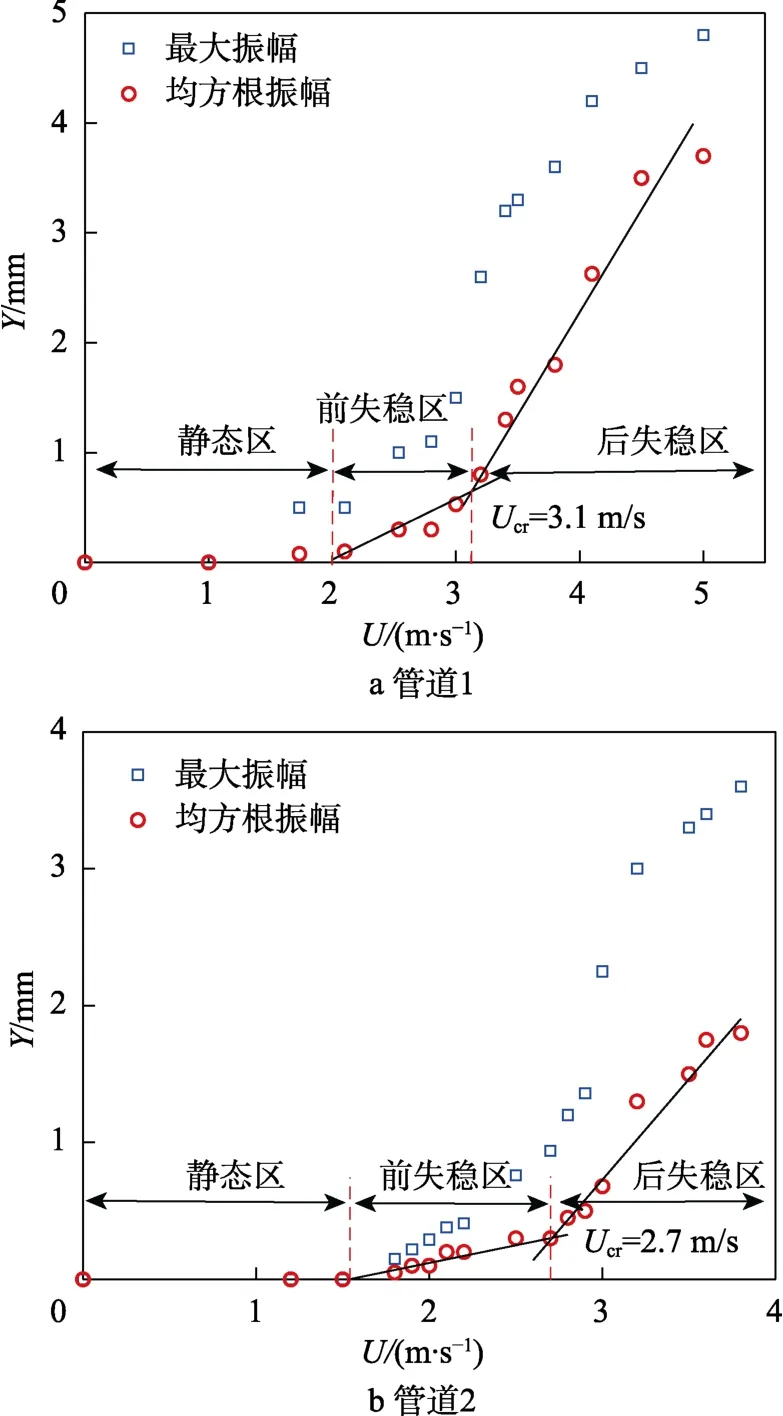
图4 不同内流流速U下的管道1和2的均方根和最大振幅Fig.4 RMS and max amplitudes for pipe 1 (a) and 2(b) with various flow velocities U: a) pipe 1; b) pipe 2

1）静态区，当流速从0开始，分别增加到约2 m/s和1.5 m/s时，2根管道几乎都没有振动，处于静态状态。

2）前失稳区，当流速U继续增加时，管道开始轻微振动。随着流速增加，管道振幅缓慢增加，此时管道处于前失稳状态。

3）后失稳区，当流速U超过临界流速Ucr时，管道发生明显失稳振动，管道的均方根RMS振幅随流速的增加而显著增大，此时管道处于后失稳状态。

一般将临界流速定义为前后2个失稳状态的交点[15,22]。管道1和2的临界流速分别为3.2、2.7 m/s。在后失稳状态，管道1和2的最大振幅分别可以达到接近5、4 mm，振幅同管道的壁厚接近，振动失稳现象非常明显，由此可见，内流流速是激发管道振动失稳的关键因素。管道1的临界流速大于管道2，因此管道2较管道1更容易发生失稳现象。由表1分析可知，管道1的刚度EI大于管道2，因此可知大刚度的管道比小刚度管道更加稳定。

在不同浸没深度时，管道1的RMS振幅随内流流速U的变化情况如图5所示。管道RMS振幅随着浸没深度的增加而显著减小。其主要原因是，随着浸没深度的增加，外部流体对管道产生的黏性阻尼和附加阻尼增加，加速了管道能量向外部流体的耗散，因而管道振幅减小。由此可见，浸没深度也是内流激发管道振动失稳的关键影响因素。

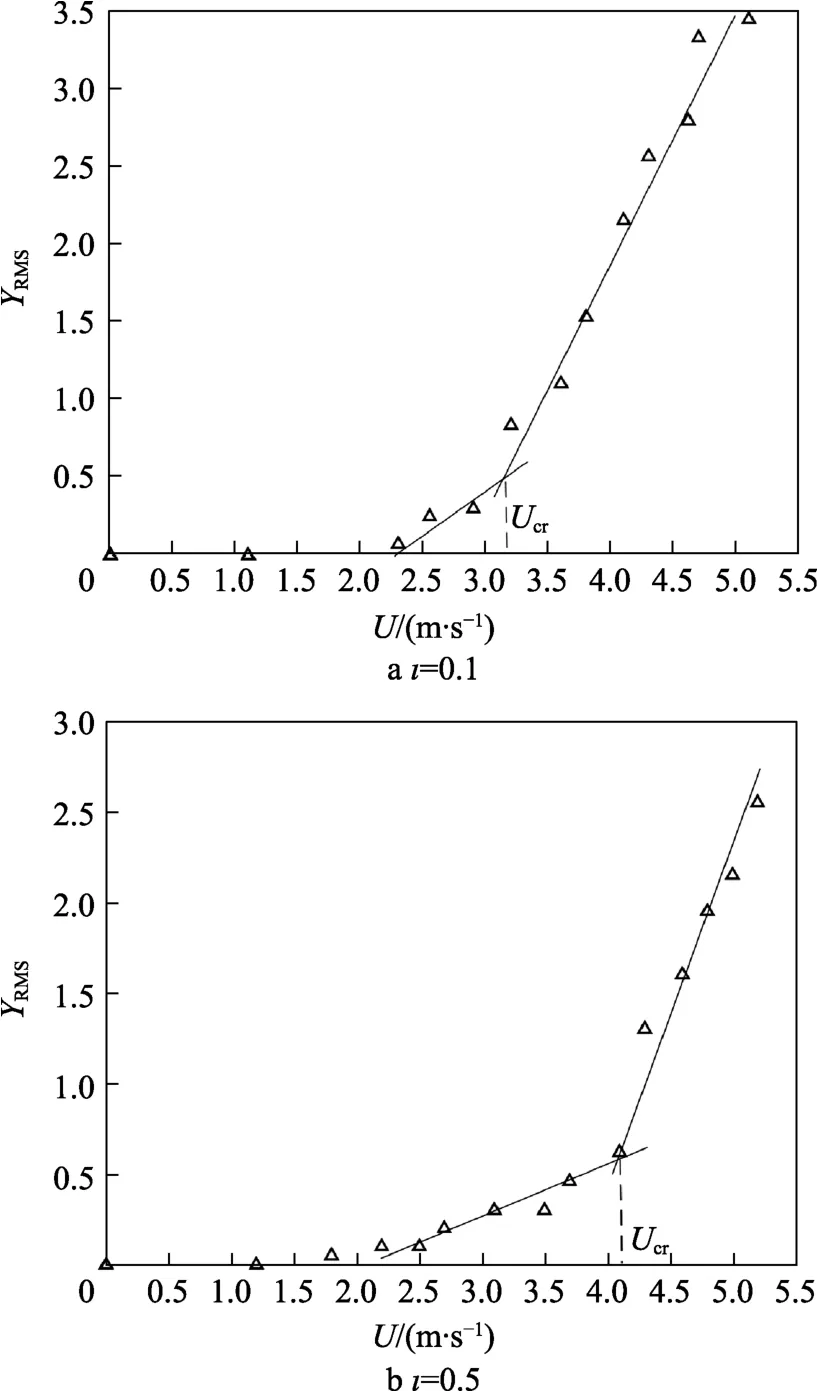
图5 管道1的均方根振幅随内流流速U变化Fig.5 RMS vibration amplitude with various internal flow velocity U for pipe 1

2.3 时频特性和相位变迁

从2.2节分析可知，内流流速是影响管道失稳振动的关键参数。当管道浸没深度ι=0.05时，管道1在不同内流流速时的时频图如图6所示。在该流速范围内，第一阶模态主导管道振动。第一阶模态频率从0.41 Hz（U=2.5 m/s）一直增加到0.45 Hz（U=5 m/s）。这主要是因为随着内流流速的增加，在管道的自由端获得更多的流体能量，管道和内流组成的系统能量增加，管道的振动频率随之增加。

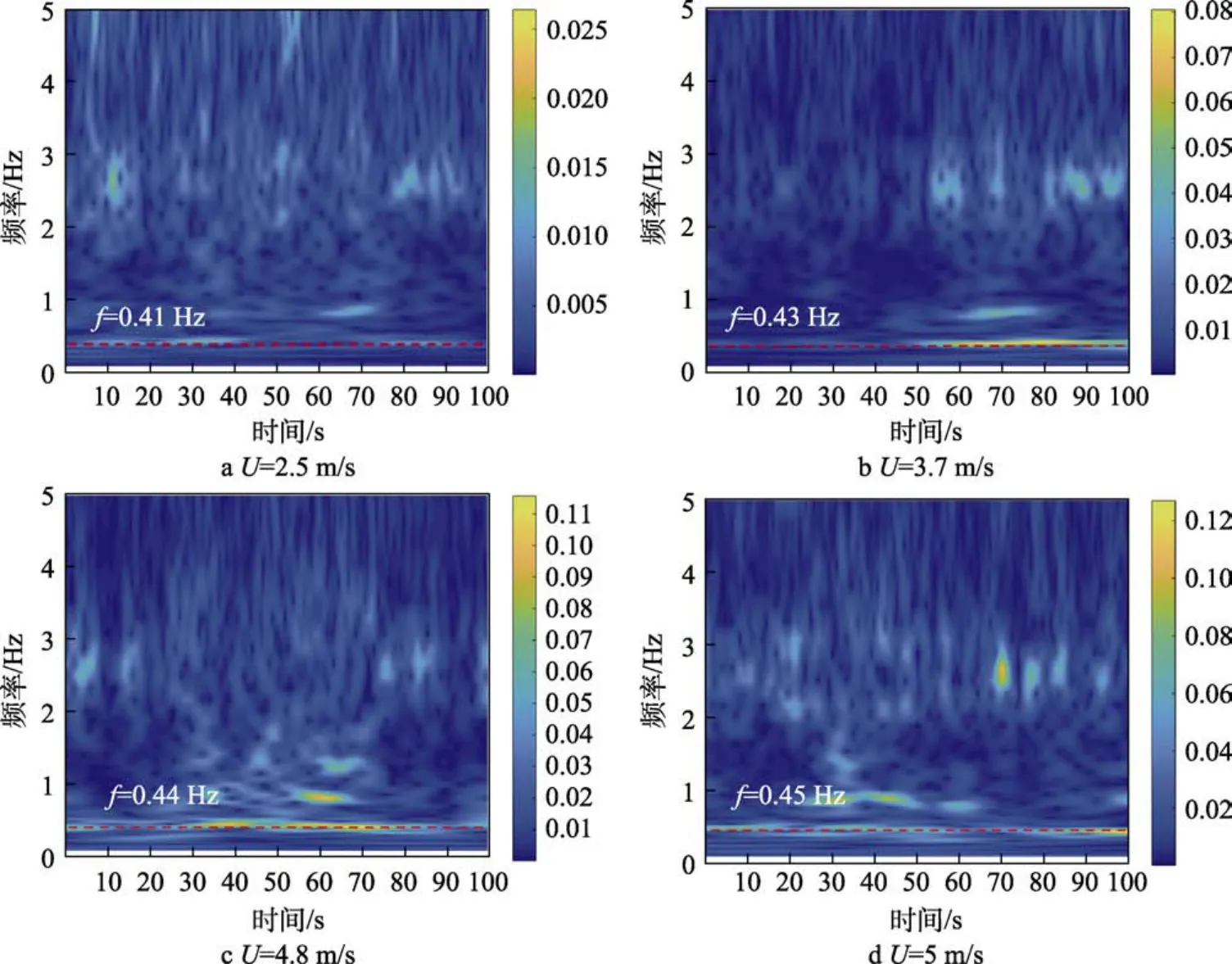
图6 当管道浸没深度为ι=0.05时管道振动响应的时频特性Fig.6 Time-frequency characteristics of the vibration response for pipe 1 with ι=0.05 under various internal flow velocities

不同内流流速下管道振动的相位图如图7所示。在前失稳状态U为2.1～2.5 m/s内，管道振动轨迹表现出向椭圆收敛的近周期行为。在后失稳状态图U为3.4～3.7 m/s内，振动轨迹包络线明显膨胀。随着流速的增加，相位图中椭圆的中心开始扩散，相位图进一步膨胀，振动幅值大幅增加，此时管道的振动呈现明显的扩展周期行为。

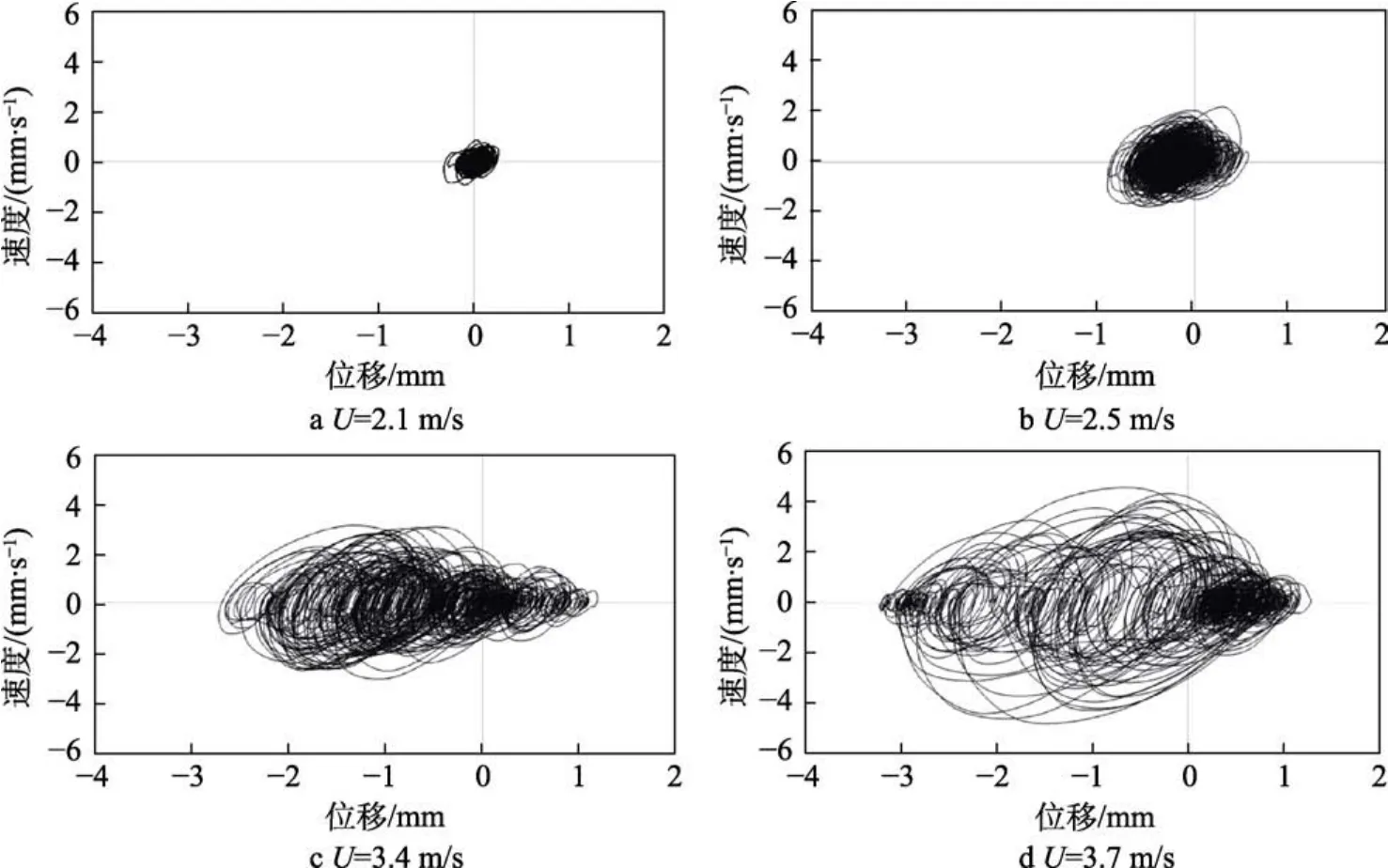
图7 当管道部分浸没在水中ι=0.05时在U为2.1～2.5 m/s的近周期行为和在U为3.4～3.7 m/s的扩展周期行为Fig.7 Nearly-periodic behavior at U=2.1～2.5 m/s and expanding behavior obtained at U=3.4～3.7 m/s for pipe with ι=0.05

2.4 管道内流激振频率

不同浸没深度时，管道振动的频率随内部流速U的变化情况如图8a所示。可以看出，浸没深度对管道颤振频率的影响并不显著。以最小和最大的浸没深度ι=0.05和ι=0.6对比，浸没深度差异约12倍，但振动频率的差异范围在10%左右，且随着内流流速的增加，振动频率差异逐渐减小。由图8a可知，管道振动频率随着内流流速U显著增加。对于浸没深度比在0.05≤ι≤0.6时，管道1的振动频率为0.38～0.45 Hz，而管道1的自然频率为0.55 Hz，管道在内流激励下的振动频率总是小于其自然频率。不同浸没深度时，管道振动频率随内流流速基本呈现线性递增的关系，利用如式（3）所示线性关系拟合离散数据点：

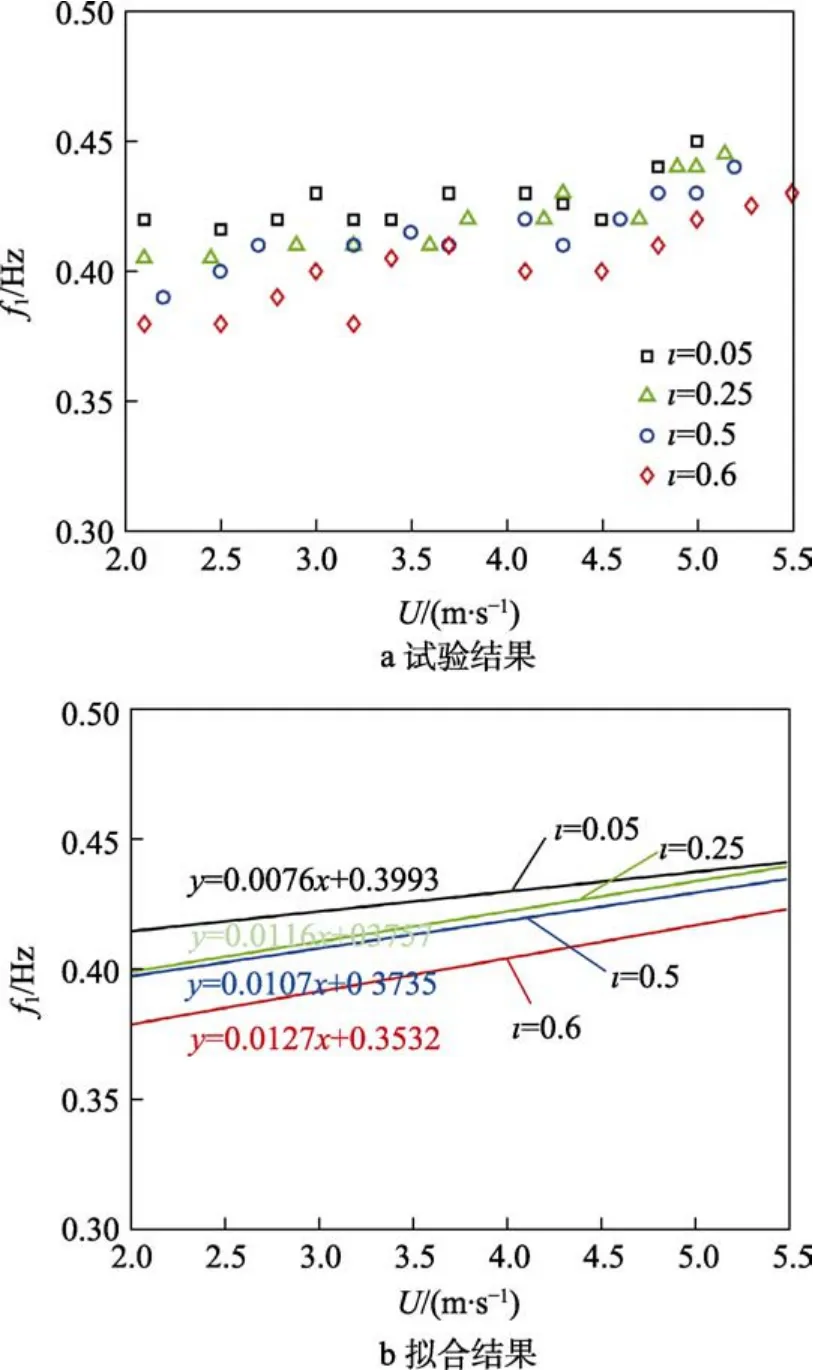
图8 管道振动频率在不同浸没深度时随内流流速U的变化Fig.8 Variation frequency of pipe with the internal flow velocity U for different pipe submersion depths: a) experimental results; b) fitting results

由拟合关系（3）可知，当ι为0.05、0.25、0.5、0.6时，k分别对应为0.007 6、0.011 6、0.010 7、0.012 7，b分别对应为0.399 3、0.375 7、0.373 5、0.353 2。斜率k和截距b由管道材料、尺寸和浸没深度决定。利用图8b的拟合关系可以得到在其他流速范围内的管道内流激振频率。

本试验研究以海洋油气和深海采矿等海底资源垂直输送为工程背景。在实际的海底资源开发中，垂直细长管道长度一般超过1 000 m，而管道外径在1 m左右，因此管道的细长比一般超过1 000。本试验研究由于试验条件的限制，管道1和2的细长比分别为80和63。在现有公开发表的管道振动失稳试验研究的相关文献中，本试验的管道细长比较其他学者更接近工程实际。几何相似一直是国内外细长管道失稳振动试验研究的一个制约因素。

本试验的目的旨在通过系列模型试验来研究影响管道振动失稳的关键敏感性参数，揭示这些关键参数对管道振动特性的影响规律，进而定性评估全尺寸悬臂管的振动特性。试验研究发现，内流流速、浸没深度和管道刚度是影响管道振动失稳的关键敏感参数，这些敏感参数与管道失稳振动的特征参数（如振动幅度、频率、临界流速和相位等）紧密相关。本试验的结论可直接应用到实际工程中全尺度管道的振动失稳特性的定性分析中。