基于优化深度极限学习机的船舶柴油机故障诊断

卢佳音 徐飞翔 林叶锦

(大连海事大学轮机工程学院 辽宁 大连 116026)

0 引 言

船舶柴油机安全可靠地运行对船舶的运行和船员人身安全至关重要,故障诊断技术作为智能运维技术的有机组成部分而受到广泛关注。目前基于数据驱动的故障诊断方法在故障诊断领域得到广泛的应用,常用的有支持向量机、BP神经网络和深度信念网络等,极限学习机(Extreme Learning Machine,ELM)作为一种前馈单隐层神经网络最早由Huang等[1]提出,因其参数设置简单,不需要进行迭代更新,受到广泛应用。但是,单层的网络结构不能很好地对数据特征进行提取,因此,文献[2]提出了多层极限学习机(Multilayer Extreme Learning Machine,M-ELM),M-ELM仅仅是将极限学习机进行简单的堆叠,文献[3]将M-ELM用于航空发动机部件的故障诊断,取得良好效果,但其仅采用单核函数。文献[4]在稀疏极限学习机自动编码器的基础上,提出了一种新的深度极限学习机(Hierarchical Extreme Learning Machine,H-ELM),文献[5]提出了多维特征提取的H-ELM并利用多核极限学习机进行最终分类,诊断效果虽然提高,但是隐含层的节点数量太多,占用计算资源较多,复杂度也有较大提高,而且多核函数的核参数选取较困难。

本文在改进人工生态系统优化算法(IAEO)部分,首先利用Hammersley点集对个体初始化,提高了算法的寻优能力。其次,引入经典的非线性递减策略和混沌序列来平衡算法的探索和开发能力。最后,引入烟花算法的爆炸操作和高斯变异,提高了算法跳出局部最优的能力。网络模型部分,先利用H-ELM对输入数据进行逐层特征提取,然后采用混合核极限学习机对提取到的特征进行高维度映射并分类。因为混合核极限学习机中核参数、正则化系数和比例系数对分类性能影响较大,所以利用IAEO对核参数、正则化系数和比例系数进行寻优,有效克服了参数靠经验选取的缺点。将深度混合核极限学习机(Deep Hybrid Kernel Extreme Learning Machine,DHK-ELM)在通用数据集上与其他算法进行了对比。最后将IAEO-DHK-ELM应用到船舶柴油机故障诊断中,结果表明本文算法有较高的诊断精度和泛化能力。

1 人工生态系统优化算法

人工生态优化算法[6]是将食物链中的能量传输方式和生物在生态链中的位置进行数学建模而产生的一种新的自然启发优化算法。在最小化问题中,适应度值越大能量等级越高,最大适应度值的个体为生产者。人工生态系统优化算法的数学模型如下:

1) 生产者算子:每次迭代时生产者算子利用当前最优位置产生一个新的生产者位置。

x1(t+1)=(1-a)xn(t)+axrand(t)

(1)

a=(1-t/T)r1

(2)

xrand=r[U-L]+L

(3)

式中:n是个体个数;t是当前迭代次数;T是最大迭代次数;r1是[0,1]之间的随机数;r是范围在[0,1]之间的随机向量;xrand是搜索空间中一个随机产生的位置;U和L分别是解空间的上下界矩阵。

2) 消费者算子:首先提出了一个带有Levy Flight特征的因子:

(4)

式中:N(0,1)是一个平均值为0、标准差为1的正态分布随机数。

对消费者获取能量的方式进行数学建模:

(1) 食草生物:

食草生物能量来源于生产者,数学模型为:

xi(t+1)=xi(t)+C·(xi(t)-x1(t))

i∈[2,3,…,n] (5)

(2) 食肉生物:

xi(t+1)=xi(t)+C·(xi(t)-xj(t))

i∈[3,4,…,n],j=randi([2i-1]) (6)

(3) 杂食生物:

xi(t+1)=xi(t)+C·(r2·(xi(t)-x1(t)))+

(1-r2)(xi(t)-xj(t))

i∈[3,4,…,n],j=randi([2i-1]) (7)

式中:r2是一个[0,1]的均匀随机数。所有个体更新位置后,进行择优选取。

最后,利用分解者算子来对所有个体进行位置更新。

3) 分解者算子:

个体位置更新公式如下:

xi(t+1)=xn(t)+D·(e·xn(t)-h·xi(t))

i=1,2,…,n(8)

D=3u,u～N(0,1)

(9)

h=2·r3-1

(10)

(11)

式中:r3是[0,1]之间的一个均匀随机数。

人工生态系统优化算法步骤如下:

(1) 初始化个体位置xi,计算适应度fiti,记录当前最优解xbest。

(2) 判断是否达到最大迭代次数:若否,则继续执行步骤(3)到步骤(6);若是,则结束计算,返回最优解xbest。

(3) 对于生产者x1根据式(1)更新位置。

(4) 对于消费者xi(i=2,3,…,n)分三种情况:

ifrand<1/3

被选为素食生物根据式(5)更新位置。

elseif 1/3≤rand≤2/3

被选为肉食生物根据式(6)更新位置。

else

被选为杂食生物,根据式(7)更新位置。

(5) 计算个体适应度,择优选取并更新当前最优解xbest。

(6) 分解算子:根据式(8)对所有位置进行更新,计算适应度值,进行降序排列,适应度值越高能量等级越高。更新当前最优解xbest,返回步骤(2)。

2 改进人工生态系统优化算法

2.1 基于Hammersley点集初始化

人工生态系统优化算法中个体初始化位置随机产生,容易发生初始化位置在解空间分布不均匀的情况,减小了可寻优范围,增大了陷入局部最优值的可能性。Hammersley点集相较于随机方法产生的个体在空间上分布更加均匀[7],因此,利用Hammersley点集进行初始化。图1以二维为例展示了两种方法的初始点分布情况,图1(a)为Hammersley点集,图1(b)为随机法。

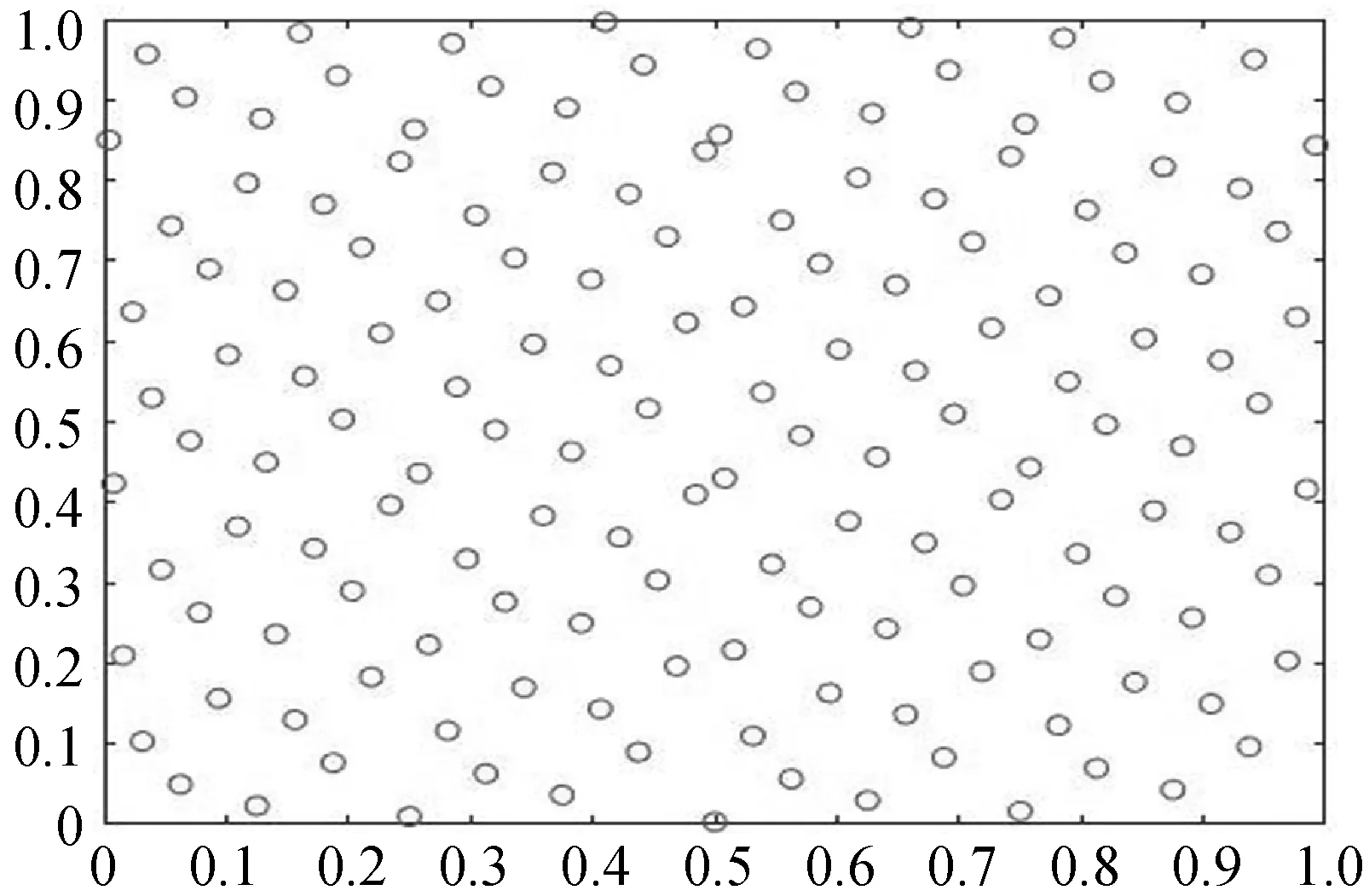
(a)

Hammersley点集是在Van der Corput序列的基础上构造的一种低差异度点集。

以b为基的Van der Corput序列为:

{xn=φb(n),n∈N},N为元素个数,b≥2

式中:b进制根数逆函数φb:N0→[0,1)。

(12)

包含N个点的以b1,b2,…,bd-1为底Hammersley点集为:

HN,b1,b2,…,bd-1={H0,H1,…,HN-1}

(13)

(14)

式中:n=0,1,…,N-1在搜索空间[Up,Low]D,D为空间维数,Up和Low表示搜索空间的上下界,初始个体数量为N。个体的初始化位置为:

xi=Low×rand(1,D)+Hi(Up-Low)

(15)

2.2 非线性递减与混沌序列

在式(1)中a用来调整算法的探索和开发,由于a是随机产生,不能很好地平衡不同阶段算法探索和开发能力,因此,引入在优化算法领域经典的非线性递减策略,使算法前期充分进行探索,后期下降较快,加快收敛。

b=π(t/T)a=(1-sin(b/2)2)

(16)

混沌作为自然界普遍存在的一种非线性现象,因混沌变量具有随机性、遍历性和规律性的特点,被广泛用于优化算法的改进。本文选用Iterative混沌序列代替分解者算子中的r3来提高算法的探索性能。Iterative混沌序列的表达式如下:

(17)

因为Iterative混沌序列的范围是[-1,1],所以需要将其归一化到[0,1]。

2.3 爆炸操作和高斯变异

为了提高算法跳出局部最优解的能力,将烟花算法[8]中爆炸操作和高斯变异机制引入到人工生态系统算法中,选择适应度最好的个体来用于对全部个体进行位置更新。根据式(18)、式(19)计算爆炸半径Ai和产生的火花数目Si。

(18)

(19)

式中:fmax、fmin是目前个体中适应度的最大和最小值;A是产生火花的爆炸半径常数因子;M是产生爆炸火花数的常数因子;ω为机器最小数,避免发生除零操作。

利用式(21)和式(22)对根据式(20)来选择的Z个维度进行操作,产生爆炸火花。

z=round(d·rand(0,1))

(20)

h=Ai·rand(-1,1)

(21)

(22)

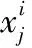
为了提高个体的多样性,随机选择一些个体进行高斯变异。同样是利用式(20)选取Z个维度,根据式(23)和式(24)来产生高斯变异火花。

g=Gaussian(1,1)

(23)

式中:Gaussian(1,1)表示均值为1、方差为1的高斯分布。

(24)

2.4 仿真实验与结果分析

选取四种非线性基准函数对比IAEO、AEO、MFO、GOA、SSA和PSO[6,9-12]的性能,基准函数的属性如表1所示。实验中所有算法的种群规模都设为30,最大迭代次数设为500,每个函数独立运行30次,最后统计结果的最优值、最差值、平均值和标准差。IAEO选用Iterative混沌序列,火花的最大和最小个数为200、10,高斯火花个数为30,MFO的r从-1到-2线性递减,GOA的cmax=1,cmin=0.000 04,WOA中A从2递减到0,C为分布在[0,2]的随机数,SSA中更新位置公式选择的判定条件设为c3<0.5,PSO惯性权重从0.9到0.2线性递减,c1=2,c2=2,实验环境为Windows 7专业版64位操作系统,Inter Core i7-3770 CPU @ 3.4 GHz处理器,16 GB RAM,软件为MATLAB 2016b,实验结果如表2所示,平均收敛曲线如图2所示。

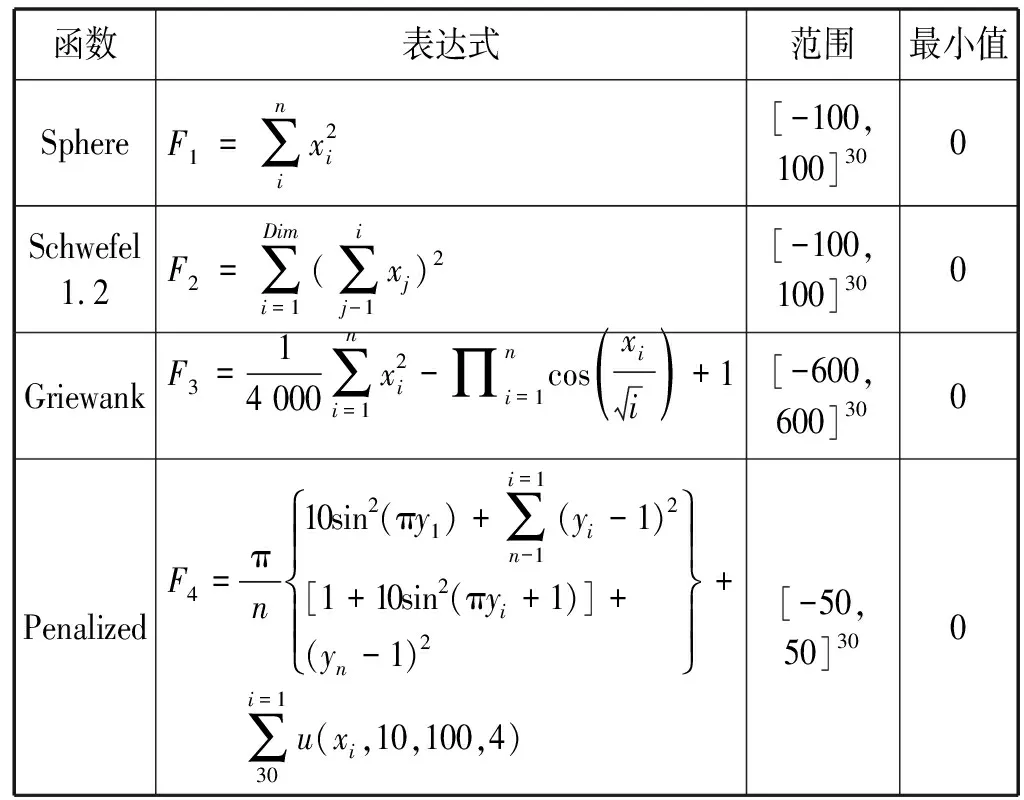
表1 四种非线性基准函数

表2 结果对比

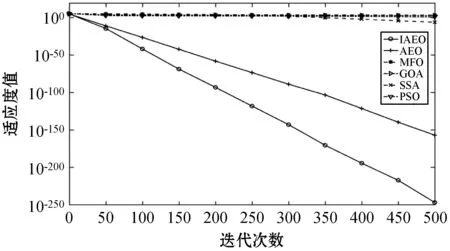
(a) F1

由表2数据可知,IAEO算法在函数F1、F2、F4上的表现好于其他算法,具有更高的收敛精度。IAEO和AEO在F3上寻到的最优值相同,但是IAEO的收敛速度更快。

3 深度极限学习机模型

3.1 极限学习机与混合核极限学习机

极限学习机中输入层与隐含层之间的权值和偏置可以随机选取不需要进行迭代调整,具有参数设置简单、训练速度快的优点,但也存在着容易过拟合、可控性和鲁棒性差等缺点。之后,Huang等[13]将核函数引入到极限学习机中,利用核函数代替点积计算,可以将样本从向量空间映射到高维特征空间,从而避免陷入“维数灾难”。

极限学习机的基本知识如下:

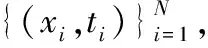
(25)

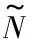
(26)

(27)

式(25)可以写成:

Hβ=T

(28)

β=H†T

(29)

式中:H†为Moore-Penrose广义逆。加入正则化系数C来提高算法的稳定性和泛化能力,则式(29)变为:

(30)

当隐含层输出矩阵H未知时,引入核函数则有:

ΩELM=HHT

(31)

ΩELMij=h(xi)·h(xj)=K(xi,xj)

(32)

核极限学习机的输出为:

(33)

核函数根据受测试点周围值影响范围的大小分为局部核函数和全局核函数,局部核函数有很好的学习能力,全局核函数有很强的泛化能力[14]。常见的局部核函数有径向基核函数,全局核函数有多项式核函数和感知器核函数。将局部核函数和全局核函数进行线性组合可以很好地平衡核函数的学习能力和泛化能力。

图3是径向基核函数、感知器核函数和它们线性组合形成的混合核函数在测试点0.05处的曲线,其中径向基核函数的σ分别取值0.1、0.3和0.5;感知器核函数的ν=10,c分别取值1、2和3;混合核函数的比例系数λ分别取值0.1、0.3和0.5,σ=0.5、ν=10、c=3。

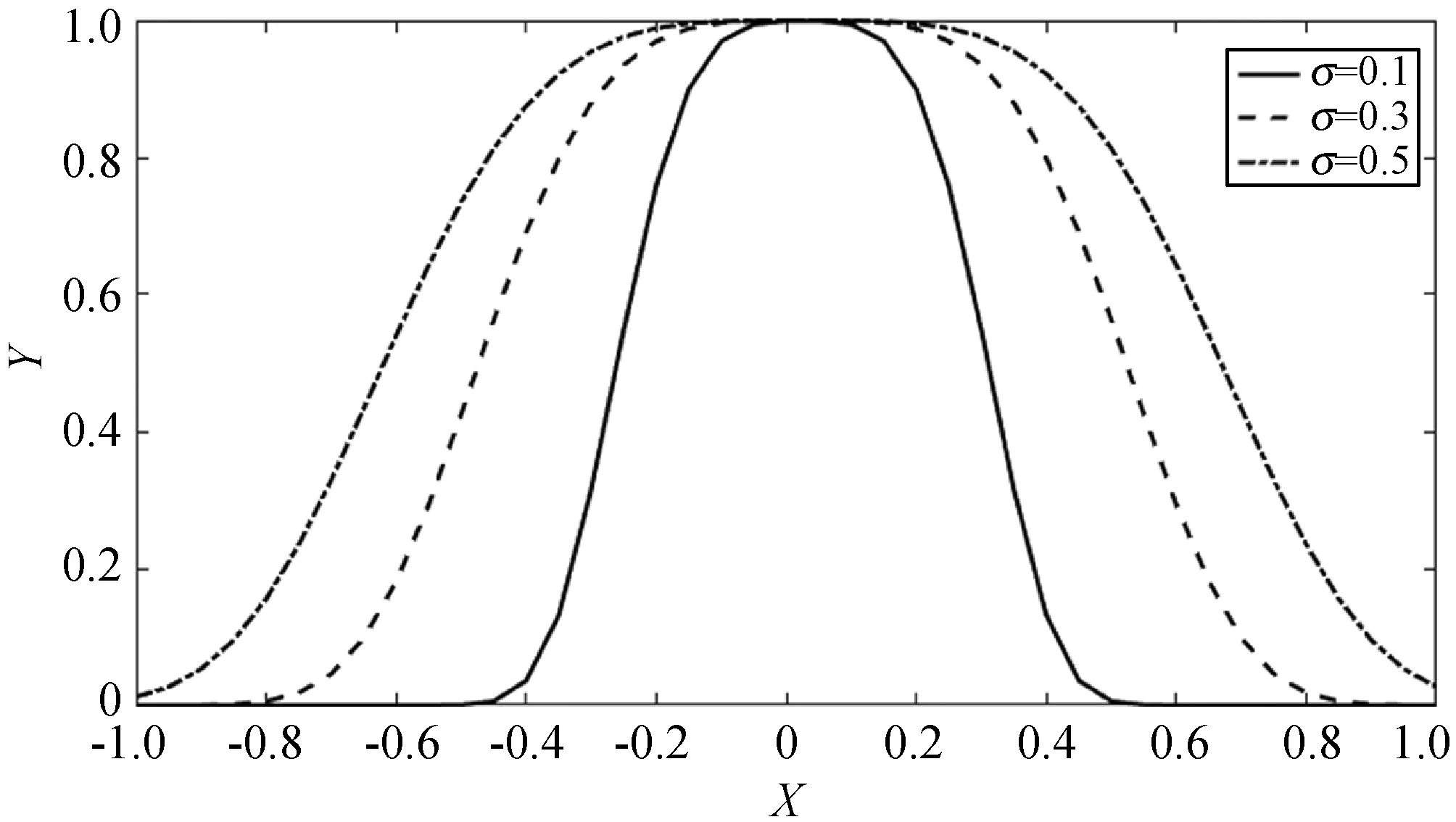
(a) 径向基核函数

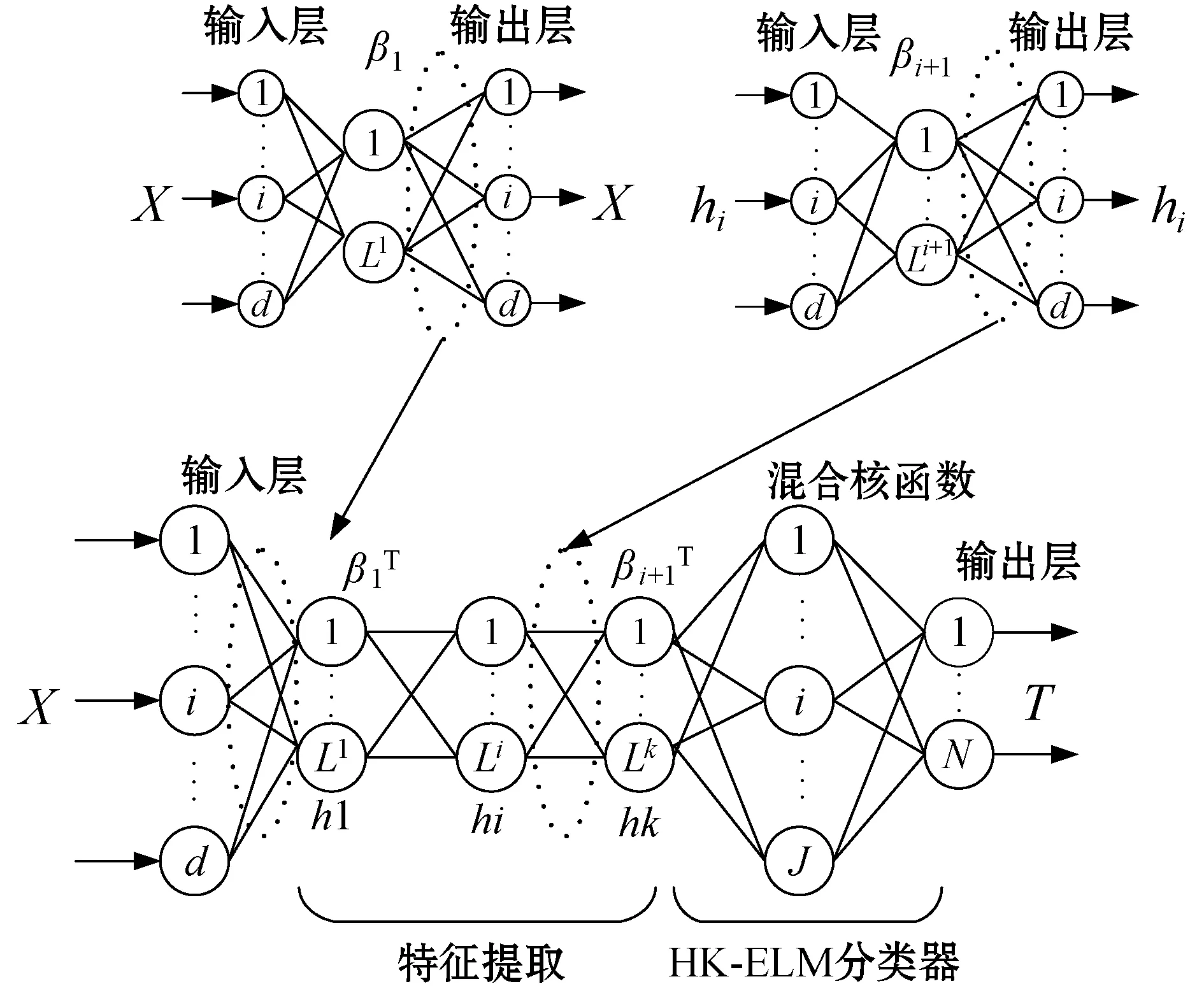
图4 深度混合核极限学习机网络结构

可以看出径向基函数在测试点附近学习能力强,但是泛化能力差,且σ越小学习能力越强。感知器核函数有很强的泛化能力,且c越大泛化能力越好。混合核函数则较好地平衡了核函数的学习能力和泛化能力。

本文采用径向基核函数和感知器核函数线性组合形成混合核函数[14],表达式如下:

(1-λ)tanh(ν(x·xi)+c)

σ>0,0≤λ≤1 (34)

式中:第一项是径向基核函数,第二项是感知器核函数,λ是比例系数。

3.2 深度极限学习机

单层极限学习机对数据特征的提取能力较差,文献[4]提出了多层极限学习机。H-ELM是将多个稀疏极限学习机自编码器进行堆叠形成的深层网络结构,相较于其他深度神经网络,具有网络参数不需要微调、训练速度快的优点。H-ELM最后采用ELM进行分类,在维度高的情况下运算复杂、泛化性能较差。因此,利用上文中提到的混合核极限学习机代替ELM对提取到的特征进行高维度映射并分类,这种算法称为深度混合核极限学习机(Deep Hybrid Kernel Extreme Learning Machine,DHK-ELM)。

因在网络结构确定的情况下,正则化系数C、核函数中的核参数σ、ν、c和比例系数λ对分类效果影响较大,故采用IAEO对上述参数进行寻优。基于IAEO-DHK-ELM的分类模型的流程如图5所示。

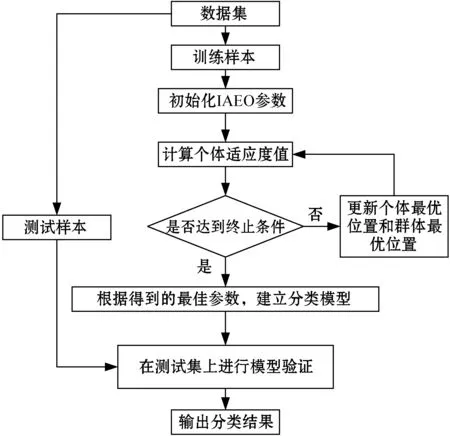
图5 IAEO-DHK-ELM流程

稀疏极限学习机编码器让输入等于输出,输出权值β即输入数据的一种特征表示:

(35)

每层的输出矩阵作为下一层的输入:

Hi=g(Hi-1·β)

(36)

3.3 标准数据集分类性能对比

将DBN[15]、M-ELM、H-ELM和IAEO-DHK-ELM算法在UCI机器学习库的标准数据集上进行对比,考虑到不同网络结构的最佳隐含层数不同,DBN在2个隐含层,其他选用3个隐含层时效果最好[3]。每层的节点个数依靠经验选取。DBN预训练阶段的RBM训练次数为50,微调训练次数为500,激活函数为Sigmoid函数,Diabetes和Wine的批训练数分别设置为16和12,Wi-Fi的批训练数设为100。IAEO初始个体设置为30,最大迭代次数为20,其他参数与前文相同。除IAEO-DHK-ELM外每个算法独立运行30次,结果取平均值,表3为数据集属性。

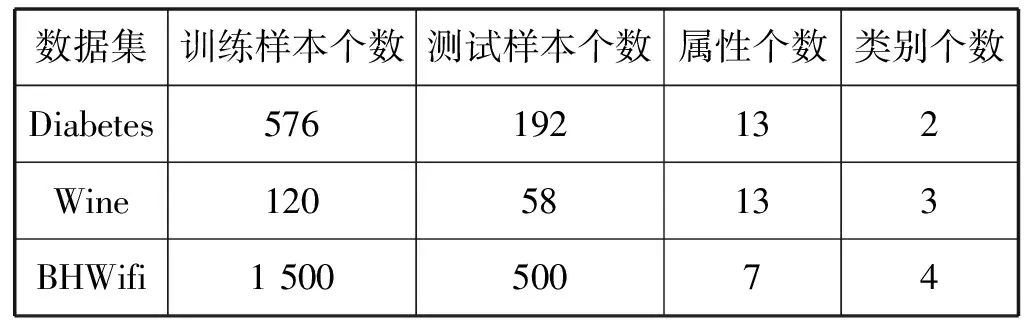
表3 标准数据集属性

从表4看出在Diabetes数据集上M-ELM与H-ELM表现差不多,IAEO-DHK-ELM的表现最好,DBN次之,在Wine数据集上四种算法都达到了较高的分类准确度,其中IAEO-DHKELM表现最好,M-ELM的表现次之,H-ELM的表现最差。

表4 标准数据集测试结果

4 船舶柴油机故障诊断

利用船舶柴油机实物进行故障模拟,成本较高,对机器具有一定的破坏性。因此,本文利用AVL BOOST软件建立燃油模式下的MAN &B W 8L51/60DF船舶柴油机模型进行故障模拟。

MAN &B W 8L51/60DF船舶柴油机的主要参数如表5所示。

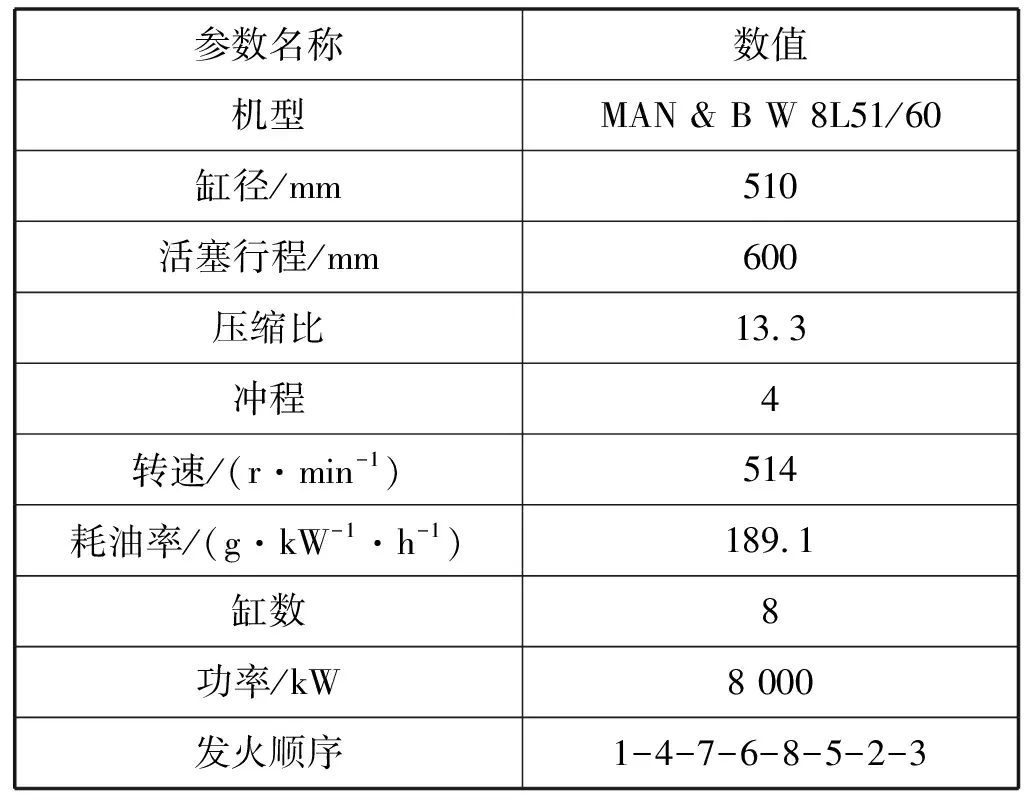
表5 柴油机集参数

柴油机仿真模型如图6所示,其中:SB1、SB2为系统边界;TC1为废气涡轮增压器;CO1为空冷器;PL1、PL2分别为进排气总管;C1-C8为气缸;MP1-MP3为测量点;J1-J16为连接点;E1为发动机;其他连线为管道。

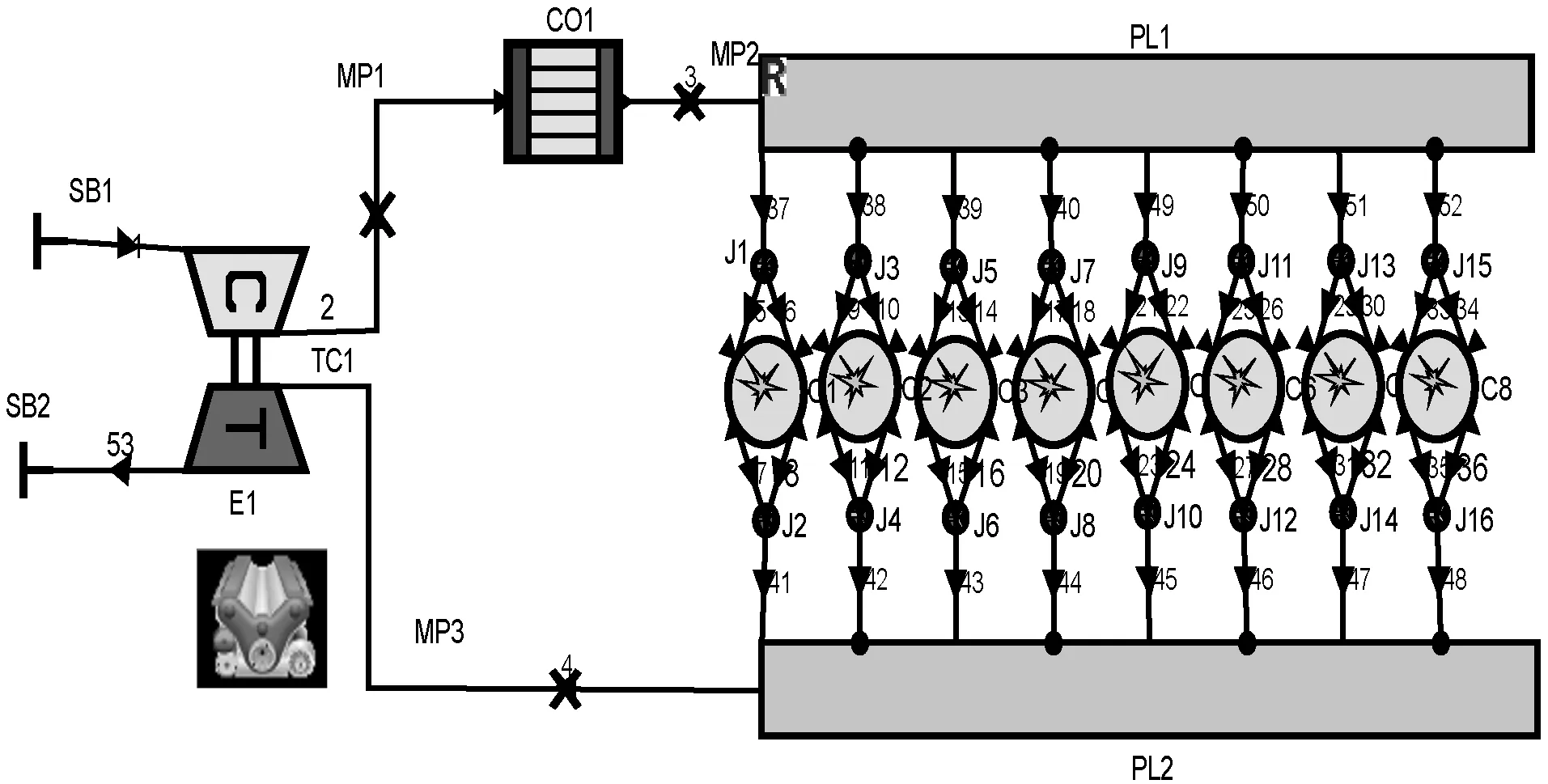
图6 柴油机仿真模型

模型验证:将燃油模式额定工况下船舶柴油机仿真模型的主要参数值与台架实验数据进行比较如表6所示。

表6 性能参数对比

可以看出船舶柴油机仿真模型的运行参数值与台架实验的参数值误差在4%以内,满足一定的精度要求,可以将其用于故障模拟。

本文共选取五种状态进行模拟:正常(F1)、喷油提前(F2)、喷油滞后(F3)、压气机效率下降(F4)和空冷器效率下降(F5)。运行50个循环,每种状态得到50组数据,共250组数据。随机选取200组数据组成训练集,50组数据组成测试集。采集的有柴油机功率、平均有效压力、最高爆发压力、耗油率、增压器出口压力、增压器出口温度、空冷器出口压力、空冷器出口温度、排气总管压力、排气总管温度、涡轮后排气温度和压力升高率共12个热工参数,对故障数据进行归一化处理,采用-1、1对状态标签进行多维编码。

算法参数设置:DBN预训练阶段的RBM训练次数为50,微调训练次数为500,将批训练数设为10,激活函数为Sigmoid函数。IAEO初始个体数为30,最大迭代次数为20,其他参数与前文相同,每个算法运行一次。仿真模型关键参数运行曲线如图7所示。

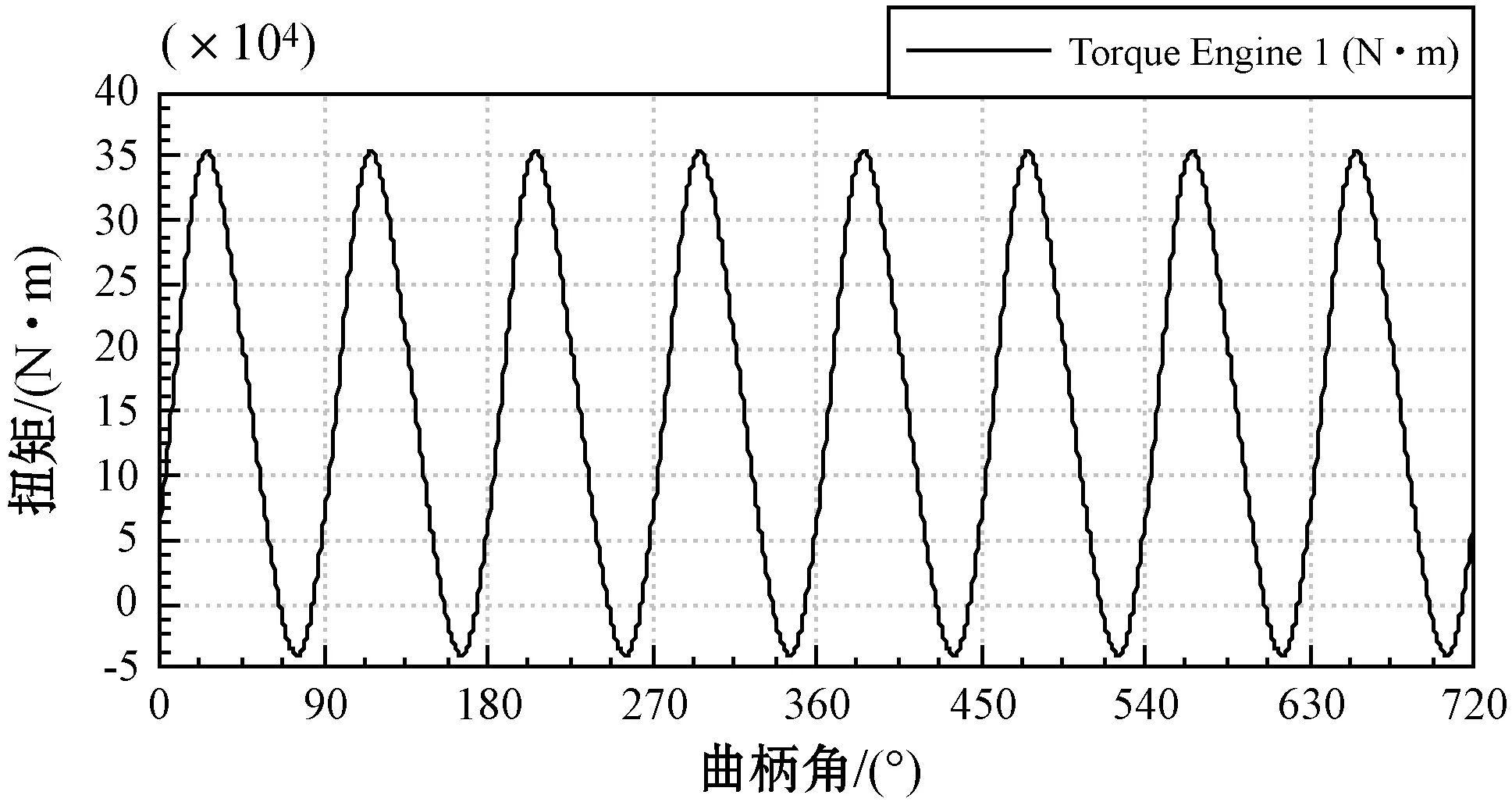
(a) 柴油机扭矩曲线

从表7看出IAEO-DHK-ELM在训练数据集和故障数据上都表现出较好的分类准确度。混合核函数的高维映射能力使其具有更强的分类能力和泛化性能,利用IAEO进行参数寻优较好地克服了依靠经验选取参数的缺点,缩短了模型调试的时间。

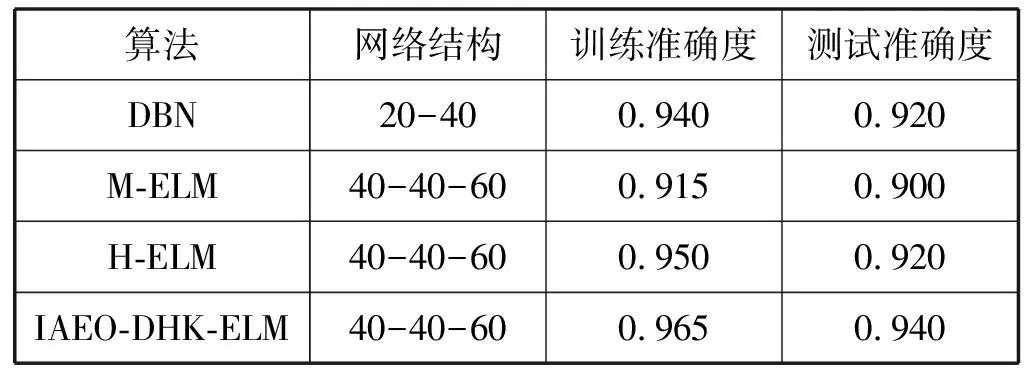
表7 故障数诊断结果

图8是各个算法在测试集上的诊断结果的混淆矩阵。四种算法都能准确地识别正常(F1)和喷油提前(F2),主要是因为喷油提前会造成气缸内最大爆发压力和最大压力升高率显著升高,特征明显易于识别。在喷油滞后(F3)和压气机效率下降(F4)间容易识别错误,原因是两种故障类型在功率下降、耗油率增加和排温升高等热工参数变化趋势相似。其中IAEO-DHK-ELM在F3和F4的识别上效果最好,核函数的高维映射能力提高了识别正确率。

(a) DBN算法

5 结 语

本文利用Hammersley点集初始化个体位置,使个体具有较好的多样性和空间分布特性,非线性递减策略和混沌序列的引入改善了AEO的寻优能力,爆炸操作和高斯变异使分解算子能利用一个较优解来进行位置更新,使IAEO具有较强跳出局部最优的能力。在充分利用H-ELM对数据进行特征提取的基础上,利用混合核极限学习机对提取到的特征进行高维映射和分类,提高了模型分类准确度和泛化能力。但是,船舶柴油机仿真模型的限制导致可模拟的故障类型较少,以后可以对模型进行改进使其能够模拟更多的故障类型。另外,虽然利用IAEO来优化诊断模型的参数使网络的参数选取容易,但是训练时间也有所增加。