基于鸟群优化BP神经网络的滑坡处治后变形预测

2023-09-04曹小燕满新耀汪继平麦荣章郭云开

测绘通报 2023年5期

曹小燕,满新耀,汪继平,麦荣章,郭云开

(1. 广西交通投资集团有限公司,广西梧州 543000; 2. 长沙理工大学测绘遥感应用技术研究所,湖南长沙 410076)

滑坡变形程度是判别滑坡失稳破坏的关键参数[1-2]。滑坡变形受降雨、滑坡岩土体性质及工程活动等多因素的共同影响[3-4]。为保障人民财产与公共安全,工程中通常采用支挡、卸载等方式对滑坡进行处治,以降低滑坡位移量,提高其稳定性[5-6]。

长期以来,研究人员围绕滑坡变形情况展开了大量研究,并取得了有益进展。文献[7]采用LiDAR、高密度电法、钻探、现场调查等手段分析了川藏线折多塘滑坡的变形特点,认为该滑坡变形具有蠕滑特点,属于“蠕滑-拉裂”式滑坡;文献[8]基于累计变形判据和变形速率构建了双判据滑坡预警模型,并将该预警模型成功应用于三峡库区木鱼包滑坡预警分析;文献[9]借助统计方法研究了长江三峡库区滑坡的变形特点,总结得出边坡变形与库水位变动有明显相关性。此外,滑坡变形还受斜坡结构、滑面形态、涉水程度、渗透特性的共同影响。文献[10]借助GeoStudio计算了白水河滑坡的渗流场与变形场,并结合分形理论对滑坡演化过程进行了分析,发现白水河滑坡在变形上具有高程分带特征和滞后性,变形速率与降雨量和库水位下降速率有明显相关性;文献[11]采用GNSS技术对滑坡变形进行监测,并采用加权一阶局域方法、最大Lyapunov指数方法及BP神经网络方法对陕西泾阳庙店滑坡变形情况进行预测,结果表明BP神经网络具有较好的预测效果。

整体而言,既有研究仍主要集中于不同岩土性质与不同地貌特征下的滑坡变形特征。随着数据科学的不断发展,近年来滑坡变形预测已成为滑坡防治领域的热门话题。开展处治后滑坡位移值预测可提前掌握处治后滑坡的长期稳定性情况,对实现地质灾害预测预报与精准防治意义重大。为提前了解已处治滑坡变形情况,本文在传统BP神经网络预测方法的基础上,开发一种鸟群算法优化BP神经网络的滑坡位移预测模型,用于已处治滑坡变形预测,并基于广西某高速公路滑坡长期变形监测数据进行验证。

1 BP神经网络原理

BP神经网络一般由输入层、中间层、输出层组成,输入层与中间层、隐藏层间的神经元全部互相连接,但各层中的神经元无连接。BP神经网络的拓扑结构如图1所示。BP神经网络可通过学习已有输入数据,建立输入数据与输出数据之间的映射关系,实现多变量非线性系统分析,在各领域内被广泛应用。

图1 BP神经网络的拓扑结构

BP神经网络通常包含正向传播和反向传播。使用BP神经网络进行预测时,通常先给出一个权值,对输入样本进行正向输出,逐层处理[12];当输出值与期望值差距较大时,开始反向传播,通过不断修正中间层的权值,使总误差最小,从而达到预测的目的。

2 鸟群优化算法

2.1 鸟群优化算法原理

鸟类是一种群居型动物,其生活过程中存在觅食、警戒、飞行等行为。参考鸟群的这一特点,文献[13]提出了一种智能优化算法——鸟群优化算法。该优化算法运算速度快且具有良好的稳健性,是现阶段最先进的群智能算法之一,正在多领域逐步推广应用。

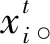
(1)鸟群中每个个体的行为具有随机性,在觅食和警戒中随机切换,这种随机性借助0～1之间的一个常量p进行判别。当随机数小于p时,鸟进行觅食;反之,则鸟进行警戒。

(2)觅食行为中,鸟群中的每只鸟借助其自身和整个鸟群的经验寻找食物,觅食行为对应的更新公式为

(1)

式中,j为1～D之间的正整数;rand(0,1)为0～1之间均匀分布的随机数;C为认知加速因子;S为社会加速因子;C与S均为正数;pi,j为第i只鸟先前最优位置;gj为种群先前的最优位置。

(3)警戒行为中,鸟群中的每只鸟都企图向群体的中心移动,导致存在竞争关系,因此各只鸟并不会直接向该群体中心移动,警戒行为的更新公式可表示为

(2)

其中

(3)

(4)

式(2)—式(4)中,a1和a2均为(0,2)之间的常数;ε为避免分母为0设置的较小常数;pFiti为第i只鸟的最佳适应度值;sumFit为鸟群中所有鸟的最佳适应度值之和;meanj为鸟群第j维的平均位置,k≠i且k为1～N之间的正整数;A1和A2分别为环境引发的间接作用和具体冲突引发的直接作用。

(4)鸟群中的鸟可以分为生产者和索取者,食物储量最高的鸟为生产者,食物储量最低的鸟为索取者。鸟群向其他位置移动时,鸟在生产者和索取者之间随机选择。生产者负责寻找食物,索取者跟随生产者寻找食物。生产者和索取者的更新公式分别为

(5)

(6)

式中,randn(0,1)表示均值为0、标准差为1的服从高斯分布的随机数;FL表示索取者跟随生产者寻找食物,FL∈[0,2]。

(5)鸟群中各个体移动过程中,假设每只鸟均以飞行间隔FQ飞向另一位置,飞行间隔FQ为正整数。

2.2 鸟群算法优化BP神经网络

BP神经网络中关键参数为权值和阈值,权值和阈值的大小与预测效果相关性大。选用鸟群优化方法对BP神经网络进行优化时,首先应确定训练集数据,然后根据BP神经网络构建方法确定BP神经网络层数与神经元数。根据鸟群算法参数选取方法确定鸟群算法的初始参数。将样本的均方误差作为鸟群算法的适应度函数,寻找最小适应度值,保留最优个体的位置,进而判断鸟群算法的终止条件。若满足鸟群算法终止条件,则用此时的最优权值和阈值训练BP神经网络,得到预测结果;若不满足终止条件,则继续进行寻优,直至算法满足终止条件后终止,再进行BP神经网络训练。鸟群算法优化BP神经网络流程如图2所示。

图2 鸟群算法优化BP神经网络流程

3 工程实例分析

3.1 工程概况

广西某高速公路滑坡区属低山丘陵地貌,地处山间河岸山坡,山体走向为北东—南西向。山坡下缓上陡,缓坡高程约为130～190 m,坡度一般为15°～25°,陡坡山体高程约为190～300 m,坡度约为45°～55°。滑坡发育区出露、揭露地层主要为第四系残坡积堆积物、第四系冲积物;基岩为泥盆系中统地层和下统那高岭组、莲花山组。自上而下地层为黏性土与卵砾石、粉质黏土、白云岩、石英砂岩、页岩、泥质粉砂岩、粉砂质泥岩、细砂岩、粉砂岩、泥质粉砂岩夹页岩。其中第四系残坡积层主要为含碎石粉质黏土,是滑坡体的主要组成物质。滑坡体呈长条形圈椅状,滑坡后缘为3～5 m高的坚硬砂岩岩壁,前缘覆盖于河流冲积阶地之上,两侧以自然冲刷的深沟为界,横向长度约830 m,纵向长度约270 m,总面积为22.41万m2。根据坡体冲沟的划分及坡体裂缝分布特征,该滑坡体被划分为6个变形体,如图3所示。

图3 广西某高速公路滑坡区地理位置

3.2 处治后滑坡位移预测模型构建

本文滑坡变形监测数据取自上述滑坡5号变形体的ZK5-5号变形监测孔。该孔孔深全长30 m,滑坡变形监测时沿监测孔每隔0.5 m布设一变形监测点。以2020年12月9日(记作第1天)监测孔变形监测结果为基准,选取自该日至2021年10月28日的23组监测孔相对变形量作为BSA-BP神经网络模型和BP神经网络模型的训练集(见表1,限于篇幅,仅列出部分监测数据),预测长时间范围内滑坡变形情况。以2021年11月26日的监测孔相对变形量作为测试集,比较BSA-BP神经网络模型和BP神经网络模型的预测效果。在上述两种模型中,时间与监测点深度为输入参数,监测孔相对变形值为预测结果。

表1 ZK5-5号位移监测孔变形监测数据 mm

选用BSA-BP神经网络模型进行预测时,首先应根据优化算法经验参数选取方法设置鸟群算法的初始参数。本次预测中,加速因子C和社会加速因子S均设置为1,a1和a2设置为1,飞行间隔FQ为5,种群个数N为20。BP神经网络模型中,中间层节点个数通常由经验公式得出[13-15],即

(7)

式中,h为中间层节点个数;m为模型输入参数个数;n为输出值个数;a为1～10之间的正整数。根据实际计算效果,本次预测BP神经网络的中间层个数为10。

3.3 预测效果评价

ZK5-5号变形监测孔2021年11月26日变形实测值和预测值对比如图4所示,分别计算BSA-BP神经网络模型和BP神经网络模型在孔深各位置处的预测误差,绘制BSA-BP神经网络模型和BP神经网络模型预测误差对比图(如图5所示)。由图4和图5可知,采用BSA-BP神经网络模型预测所得的滑坡位移值与滑坡位移实测值更接近,BP神经网络模型的最大预测误差为3.16 mm,而BSA-BP神经网络模型的最大预测误差仅为0.83 mm,较BP神经网络模型预测效果更好。

图4 Z5-5号监测孔滑坡位移实测值与预测值对比

图5 BSA-BP神经网络模型和BP神经网络模型预测误差对比

(8)

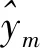
此外,相关系数也是评价数据整体预测效果的关键参数,它能反映变量之间的相关程度,通常可表示为

(9)

根据式(8)和式(9)分别计算BSA-BP神经网络和BP神经网络预测结果对应的MSE值和相关系数,两模型对应的MSE值分别为0.053 4和2.225 6,相关系数分别为0.997 6和0.968。上述结果充分说明,经过鸟群算法优化的BP神经网络预测模型对滑坡位移的预测结果更加准确,能充分满足工程实践需求。