挡风墙周围风沙流运动特性SPH数值分析
2023-09-04金阿芳热依汗古丽木沙
胡 晓,金阿芳,热依汗古丽·木沙
(新疆大学机械工程学院,新疆 乌鲁木齐 830047)
1 引言
以风沙过程为主要标志的沙漠化已成为全球最突出的生态环境问题之一。我国的沙漠及沙漠化土地面积高达128万平方公里,占据国土面积的13.3%。风沙运动对农业、牧业、交通、水利等造成了极大危害,沙害造成的直接经济损失已达到数百亿人民币[1]。风沙两相流作为一门研究沙粒在风力作用下运动规律的科学,奠定了近代风沙物理学的理论基础,是认识和研究风沙运动规律的重要组成部分,为防治地表土壤风蚀、土地荒漠化提供科学依据和理论支撑。因此研究风沙两相流运动对防沙、治沙工程来说具有重要的指导意义。
风沙两相流的研究分为直接研究和间接模拟,通常包括野外观测、风洞模拟和数值模拟等三种方法。由于前两种方法容易受外界因素干扰导致实验数据不准确,加之受场地限制需要耗费大量的人力、物力,所以计算机数值模拟方法近年来逐渐受到学者们的广泛研究和关注。Anderson 基于元胞自动机原理,模拟了沙床表面颗粒的周期性跳跃过程,并最终演化成沙波纹[2]。郑晓静等在求解沙粒垂向脉动方程的基础上,通过数值模拟得到风沙中随机沙粒运动轨迹[3]。李万清等利用随机方法生成符合自然分布规律的沙床,进而结合离散单元法(DEM)建立一套粒-床碰撞数值模拟系统[4]。亢力强等使用颗粒碰撞的欧拉-拉格朗日数值模拟方法,对风沙跃移中颗粒冲击多粒径床面的碰撞过程进行了数值计算[5]。刘博等采用离散单元法和硬球模型对单颗沙粒碰撞规律进行数值分析,模拟出颗粒的运动规律和受力状况[6]。何丽红等基于点电荷场的基本理论,建立一种风-沙-电相互作用的多场耦合模型,得到了风沙电场沿高度的分布规律[7]。现有的研究鲜有涉及用无网格法分析挡风墙对风沙两相流运动特性的影响,而在我国西北沙化地区挡风墙已然成为最为经济和应用最广的防风结构,因此挡风墙对跃移沙粒防护作用的数值模拟研究在实际工程应用中更具有实践意义。
光滑粒子流体动力学(Smoothed Particles Hydrodynamics,SPH)作为一种纯拉格朗日粒子方法,也是最早的无网格方法[8,9]。该方法最初广泛应用于天体物理领域,由于SPH方法本质上不需要借助网格,规避了网格畸变现象,因此能够处理拉格朗日格式的大变形问题。同时SPH核函数光滑长度的自适应性可以动态捕捉流场局部变化特征,通过“核函数”的近似积分将流体力学基本方程组转换成数值计算的SPH方程[10],用算法将气固两相计算域的粒子离散化,并赋予这些离散粒子所有的力学量。近年来,SPH方法已拓展应用于流体特性的数值模拟。本文引入虚粒子作为挡风墙,在此基础上对SPH搜索算法进行改进,建立了一种基于SPH方法的挡风墙-风沙流模型,以此研究自然界中挡风墙对跃移沙粒的防护效应。
2 SPH方法
2.1 SPH基本原理
SPH方法是近20多年来逐步发展起来的一种无网格方法,最初是由Lucy于1977 年提出并用来解决天体物理学中涉及三维开放空间的任意流动问题[11]。经过Benz等学者的不断改进和完善,逐渐发展成一种较为成熟的粒子模拟方法[12],推广到流体动力学的各个研究领域。其基本思想是将连续的流场离散成可以运动的粒子,利用核近似法将临近粒子关联起来,并在粒子上建立离散动力学方程,然后通过求解离散控制方程来更新粒子的位置和相应物理量信息。因其自身的无网格、自适应性、光滑性以及拉格朗日公式与近似法的和谐结合,使得SPH方法在研究大变形、复杂界面运动等问题时有着独特的优势。
2.2 核函数构造
光滑核函数决定函数近似式的形式、一致性和精度,定义粒子支持域的尺寸,所以在SPH方法中占据非常重要的地位。核函数的主要特征可以归纳为:
1) 归一性 保证连续函数积分的零阶连续性
2) 紧支性W(x-x′)=0,|x-x′|>kh
3) 非负性 对支持域内任意点x,当x-x′≤kh时,W(x-x′)≥0,|x-x′|>kh
4) 衰减性 核函数的值随粒子间间距增大而单调递减
5) 对称性 光滑核函数需为偶函数
6) 光滑性 对x支持域内任一点x′,W(x-x′,h)均无穷可导
2.3 构建风沙流SPH基本方程
SPH方程的构造通常分为两个主要步骤来进行,首先为积分表示法,其次为粒子近似法。对任意函数和光滑函数逐步积分,然后通过最近相邻粒子的值进行累加求和近似。
在SPH方法中,f(x)的积分表示式由式(1)定义

(1)
式中,Ω是包含x的积分体积,δ(x-x′)是狄拉克函数,由下式表示
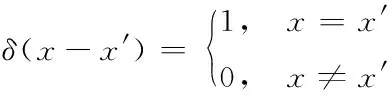
(2)
若用光滑函数W(x-x′,h)取代f(x)积分表达式中的狄拉克函数δ(x-x′),则有
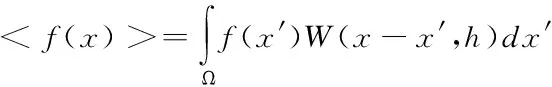
(3)
因为W不是狄拉克函数,故上式的积分表达式只能近似表示,式中的角括号<>在SPH的习惯用法中称为核近似算子标记;W(x-x′)为光滑函数;h是定义光滑函数影响区域的光滑长度。
将式(3)用粒子近似法转换为支持域中相邻粒子叠加求和的离散值。则粒子i处函数的粒子近似形式可表示为

(4)
式中,N是粒子i支持域中所有粒子的总数;xi,xj分别为粒子i和j的坐标向量;mj,ρj为粒子j的质量和密度。
2.4 控制方程的SPH离散
2.4.1 连续密度法
对速度散度应用SPH近似
(5)

2.4.2 动量方程的粒子近似法
对动量方程等号右端的梯度项直接应用SPH粒子近似法变换后可得到
(6)
2.5 双相耦合的全配对搜索法
风沙流运动是气体粒子和沙粒两种不同相粒子间的耦合运动。考虑到不同粒子对周围粒子的支持域不同,故采用SPH方法里的光滑长度来处理风沙两相流之间的耦合问题。由于目标粒子对临近粒子的搜索随时间变化而变化,因而需要寻求一种精确、有效的方法进行邻域搜索。本文针对风沙流模型提出一种新的临域粒子搜索算法即双向耦合的全配对搜索法。
图1中的大球体代表粒子的支持域,位于球心处的粒子称为目标粒子i。对于目标粒子i1(橘色大球体球心粒子)、i2(蓝色大球体球心粒子)需要根据不同的支持域半径kh,来计算它到整个问题域内每一个粒子j(j=1, 2,…, N, N是问题域内的粒子总数,图中用黄色实心小球表示沙粒,蓝色实心小球表示气体粒子)之间的距离。

图1 支持域和光滑长度的设定
本文采用了对称光滑长度,使粒子i和j互为一组相互作用的粒子对,即粒子i也在粒子j的支持域内,这样在搜索问题域内的邻域粒子时不需要再次考虑粒子i对j的影响,故缩减了一般搜索的重复计算量,提高了搜索效率。支持域半径为光滑长度h和光滑因子k的乘积,考虑到光滑长度h的选择与粒子直径相同,而双相的不同目标粒子对应不同的k因子取值,因此光滑因子k的选择决定了目标粒子对邻域粒子的影响范围。
分3种情况讨论,如图1所示(黄色小球代表沙粒,蓝色小球代表气体粒子):1)若目标粒子与作用的邻域粒子同为固体,即沙粒。这两种固体粒子只有在相互实质性的接触碰撞时方可互相作用,所以光滑因子k3=1.1*h。2)目标粒子是气相粒子,邻域粒子是沙粒,因为风沙流场中气流的运动状态和速度对沙粒的运动影响较大,所以光滑因子取k1=2.5*h。同理,粒子间的作用是相互的,若目标粒子是沙粒,邻域粒子是气相粒子,则光滑因子为k1=2.5*h。3)当目标粒子和邻域粒子同是气相粒子时,考虑到目标粒子的影响半径超过为3.0h以后对周围粒子的作用十分微弱,可忽略不记,光滑因子取k2=3.0*h。
2.6 边界处理方法
SPH数值模拟中,边界或邻近边界的粒子存在着积分时边界截断的固有缺陷,所以SPH方法并不能完全适用于整个模型区域。且位于边界或临近边界处的粒子在边界以外不存在粒子,故只受到边界内粒子的影响作用。这种单边影响作用会导致求解结果错误。为保证积分完整性,分别在计算域上下固定边界处各设置一层虚粒子,虚粒子与内部气固流体粒子参与控制方程的求解,并实时更新密度、压强等物理信息,通过对邻近实体粒子施加沿轴向的中心强排斥力,来阻止临近边界粒子的非物理穿透边界[13]。
用虚粒子处理边界的方法提高了SPH近似法在边界区域处积分求解的精度。在此基础上进一步改进虚粒子物理属性使之符合流固耦合碰撞方程,以此来代替挡风墙模型,可模拟、研究流体粒子与挡风墙作用的风沙流运动规律。
2.7 时间积分
离散近似后的SPH流体控制方程已经转化为常微分方程,可以使用数值分析中标准的计算方法,如leap-frog格式的时间积分方法,对其进行数值积分,以此来求解每一个粒子的物理变化。本文采用leap-frog格式积分,其优点是计算效率高,计算时所占用的存储低。粒子的密度、速度、内能和位置可由下面的公式递推。
t=t+Δt
ρi(t+Δt/2)=ρi(t-Δt/2)+Δt.Dρi(t)
vi(t+Δt/2)=vi(t-Δt/2)+Δt.Dvi(t)
ui(t+Δt/2)=ui(t-Δt/2)+Δt.Dui(t)
ri(t+Δt)=ri(t)+Δt.vi(t+Δt/2)
(7)
应注意的是,leap-frog格式需要满足稳定性准则CFL条件,此条件保证时间步长与光滑长度成比例,本文的时间步长取作
Δt=min(ξhi/[hiΔ.vj+cj+1.2(αcj+
βmaxj(vi-vj))])
(8)
式中,ξ为Courant系数,一般取0.3[14]。
2.8 SPH方法的程序实现
针对风沙颗粒两相流的耦合特性,在SPH方法基本计算流程的基础上,基于Linux,C/C++语言开发环境,编制了可用于风沙防护的挡风墙SPH数值模拟程序,其基本流程如图2所示。

图2 SPH计算程序流程图
3 数值计算
3.1 计算模型和计算参数
本文使用离散的方法来模拟挡风墙对跃移沙粒运动的影响。为了提高模型的精确度,在算例的计算区域内布置19940个粒子进行仿真,规模上已达到统计分析的数量级,由于大粒子群具有较高的计算时间复杂度,故仿真算力依托基于Linux编译环境的中国科技云·超算平台。计算域及初始布点如图3所示,模型宽0.02m,高0.01m;其中沙粒子个数为1990个,气体粒子个数为17950个,挡风墙采用与边界不同物理属性的虚粒子替代,粒子个数为60个。根据SPH方法中设定的光滑半径范围,选用五次样条函数的光滑函数来计算。计算中采用双向耦合的全配对法搜索邻域粒子,粒子间光滑长度的选取与粒子直径相同;时间积分选用“蛙跳法”,步长为10-6s,计算区域进出口处采用周期边界;为防止边界粒子在积分时发生边界截断导致计算崩溃,分别在计算区域的上边界和下边界各设置一层虚粒子来固定边界。这些边壁虚粒子会对靠近边界的内部实粒子产生一个强排斥力,以此来阻止实粒子对边壁的非物理穿透。初始计算模型如图3所示,入口风速随高度变化遵循指数分布规律,气体属性和自然界大气属性相同。数值计算参数如表1所示。

表1 计算参数
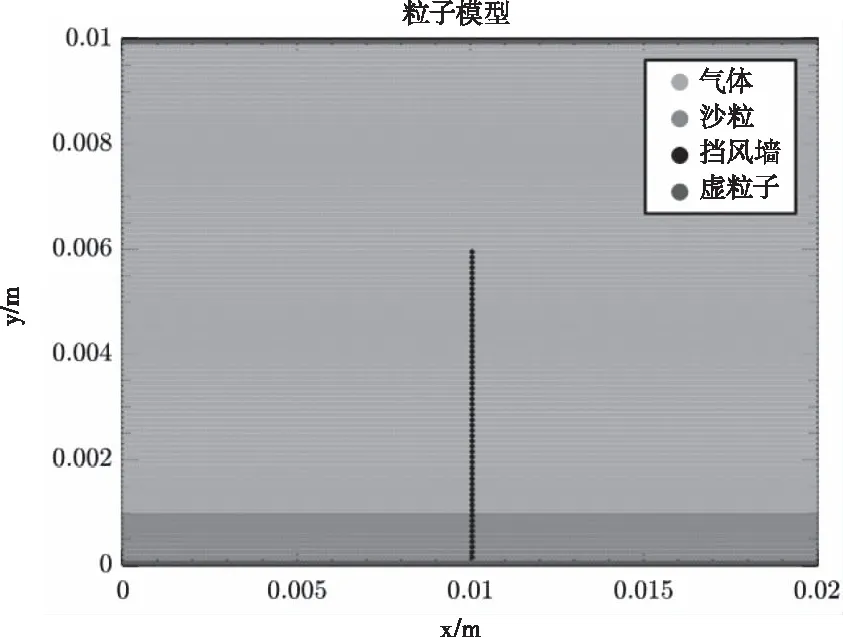
图3 初始平坦沙床挡风墙模型
4 数值计算结果及分析
4.1 挡风墙周围颗粒运动的时空变化
图4显示了时间步为(a) step=100,(b) step=6000,(c) step=10000,(d) step=14000,(e) step=25000,(f) step=30000时挡风墙周围跃移沙粒瞬时速度场的发展过程。从图中可以看出风沙流初始阶段的动力学特性与Zhang等[15]描述的基本一致。

图4 挡风墙周围风沙两相流运动的时空变化
如图a,b所示,平坦沙床最外层沙粒最先从气流中获得动量起跳,随着时间推移,大量起跳的沙粒在风场中持续获能加速,沙粒跃移高度逐渐增大,原始沙床开始松动。由于挡风墙对气流的阻挡作用,使得靠近挡风墙周围的风速呈断崖式递减,因此挡风墙附近的沙粒无法从流场中获得风能起跳。
图c,d中,跃移的沙粒群正处于成长期,整体呈上升状态,在接近挡风墙时受到风场扰动,跃移沙粒出现随机运动,部分运动的沙粒击中挡风墙后反向反弹,致使同一区域出现向前和向后的运动状态。此时,背风区跃移沙粒在重力作用下出现下降趋势。
图e,f迎风区风场中跃移的沙粒一部分因为重力作用影响开始下降,靠近挡风墙附近的另一小群沙粒由于尾流风速迅速减小,沙粒无法从周围风场获得动能来维持跃移运动也逐渐下落,堆积。而挡风墙背风区因为存在一个反向涡[16],在背风近墙区域产生一种向上的升力,上升气流又会将背风侧堆积的沙粒从沙床喷射到空气中,与传统跃移沙粒相比,这些粒子呈抛物线运动轨迹,且移动距离更短。由于跃移沙粒与挡风墙的碰撞显著降低颗粒速度,最终稳定后的风沙流会在挡风墙周围堆积。
4.2 挡风墙周围积沙分布特性
图5表示风沙流稳定后迎风区和背风区沙粒数目的横向分布。从图中可以看出挡风墙对风沙有明显的阻挡效应,距离挡风墙横向距离越近,沙粒堆积的数目越多,以挡风墙位置0.01处为中心呈正态分布特性,中间多,两边少。这正与石龙等人的相关风沙两相流模拟结果相符[17]。迎风区靠近挡风墙处的沙粒因为尾流风速减小,获取的风场动能不足以支撑其起跳跃移,实际运动则以蠕移为主。进口处跃移沙粒与挡风墙反复碰撞后逐渐失去动量,在重力作用下降落、沉积于挡风墙附近。来流风因为挡风墙的阻挡作用会在背风区形成一个反向涡,如图6所示,涡流携带的大量沙粒与挡风墙发生碰撞后也会沉积在挡风墙周围。以上现象可以看出挡风墙的存在阻碍了沙粒群的运动,大量悬浮的跃移沙粒被拦截,起到了很好的防沙效果。
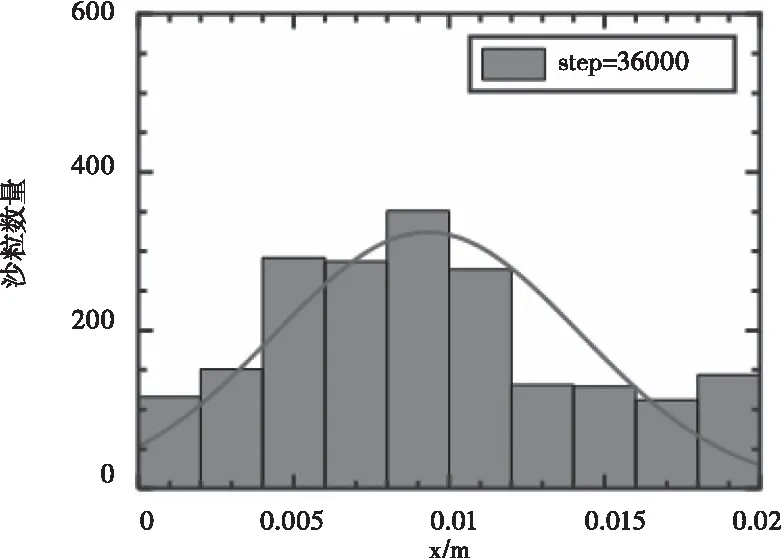
图5 挡风墙周围积沙横向分布
4.3 沙粒平均速度横向变化
挡风墙迎风和背风区域跃移沙粒平均速度横向变化如图7所示,通过对计算域内的1990个沙粒速度矢量进行集合、平均后得到沙粒平均速度,本文主要关注粒子的合成速度。不难看出,迎风区上游沙粒平均速度整体呈上升趋势,波动较大,这是因为风沙流刚起动时,进口处来流风为紊流状态,各点的流速大小和方向随时间脉动,沙粒和气体粒子间发生强烈的能量交换,使得跃移沙粒的速度和运动轨迹变化得更为复杂。中游跃移沙粒在重力负功作用消耗下平均速度大幅降低,下游靠近挡风墙的沙粒一部分因为尾流效应无法从风场获取动量演变成“蠕移粒子”,速度较低。另一部分悬浮的沙粒与该区域挡风墙发生碰撞后,落回沙床表面停止运动成为死亡沙粒[18],从而失去动能,最终导致下游挡风墙附近沙粒的平均速度急剧下降。与之相反的是背风区靠近挡风墙周围沙粒的平均速度表现出逐渐增大的趋势,此现象进一步验证了背风区反向涡的存在,该区域风向与来流风向相反,形成对沙粒有抬升作用的回流区。横向距离0.0135m之后,风场不再受挡风墙阻挡效应的影响,气流开始扩散,速度缓慢上升,并最终恢复至来流风初始状态,此时,沙粒的平均速度逐渐增大,且波动较小,与迎风区上游沙粒平均速度增加趋势相符。

图7 迎、背风区跃移沙粒平均速度横向变化
4.4 挡风墙对水平风速的影响
风沙流是一种贴近地表的风沙运动,近地表风速会对沙粒运动产生显著的影响[19],因此分析近地表风速变化趋势对研究挡风墙附近积沙形成机理具有指导意义。
图8显示了有无挡风墙对水平风速的影响情况。由图8可见,挡风墙对水平风速有明显的阻挡作用。风场中无挡风墙时水平风速遵循风速廓线的指数分布规律。增加挡风墙后,则遮挡高度以下的风速大幅降低,且阻挡效果随挡风墙高度增加而减小,当超过挡风墙高度时,水平风速开始逐渐接近无挡风墙时的风速廓线。这一现象验证了用改进虚粒子代替挡风墙进行风沙流SPH数值模拟的有效性。
5 结论
本文基于SPH方法,建立一种由改进虚粒子替代挡风墙的平坦沙床模型,并在优化邻域粒子搜索算法的基础上开发了可生成SPH粒子的风沙流程序。通过上述方法与手段,模拟了挡风墙周围风沙流运动的时空变化,可以得出以下几点结论:
1)挡风墙附近积沙量,以挡风墙为中心,呈“正态性”分布。迎风区由于挡风墙的阻挡作用使得风场中跃移沙粒与墙体发生反复碰撞而失去动量,最终变成“死亡沙粒”堆积在墙脚迎风侧。同时下游因为尾流效应的存在,靠近挡风墙的部分沙粒无法从风场中获取动量而演变成蠕移粒子。
2)背风区因为反向涡的影响,在挡风墙附近产生向上的升力,上升气流携带的大量沙粒与墙体再次发生碰撞导致动量损失,最终堆积在挡风墙背风侧。
3)风场无挡风墙时,水平风速遵循风速廓线的指数分布规律。有挡风墙时,对风速的阻挡效果随挡风墙高度增加而减小,超过挡风墙垂向高度,水平风速逐渐恢复至无挡风墙时的净风场状态。
数值模拟结果表明,挡风墙对跃移沙粒和来流风具有明显的阻挡效应。本文提出的基于SPH方法颗粒两相流仿真系统对防沙、治沙工程具有一定的借鉴意义,并能反映出沙障附近积沙的普遍规律。
