空中交通网络脆弱性分析方法研究

杨九洲,田 文,方 琴

(南京航空航天大学民航学院,江苏 南京 211106)

1 引言

伴随国家“十三五”规划的推进,“从民航大国向民航强国迈进”战略构想的实现迈入了关键阶段。2019年5月,民航局正式对外发布《2018年民航行业发展统计公报》,分析与统计其中的数据可知,从空中客运航班总次数来看,全年完成了434.58万,准点航班次数共有348.24万,平均正常比率为80.13%,平均延误时间为15分钟。2018年,民航局等各级民航组织接收到的投诉次数也达到2.07万件,因为航班出现较为严重的延误,使得旅客心生严重的不满情绪,甚至与机场以及相应航空公司产生较为激烈的冲突也常常发生,这些都会给具体的航行安全带来明显的隐患。

近年来,越来越多的学者运用复杂网络理论对现实生活中复杂网络进行复杂特征的研究,并且此类研究已经涉及多个领域。复杂网络理论是研究具有复杂性的系统结构的科学方法,它的实现基础就是图论。小世界模型(1998)[1]与无标度网络模型(1999)[2]的相继提出,使得复杂网络理论进入到全新的发展高度。在此基础上,又有诸多研究者进行了空中交通相依网络的复杂性研究。例如,Cheung和 Gunes[3]分析了美国航空运输网络,由此得出该网络存在着典型的小世界属性,相关度分布遵循了“双段幂律”分布原则;Pien 等[4]分析了欧洲航空运输网络特性;Xu[5]等人在研究美国航空运输网络时同样得出它具有显著小世界属性,度值高的城市倾向和同类城市的连接;CAIK Q等[6]对中国的航空运输网络进行了分析,表明中国航空运输网络具有指数度分布、最短路径长度等相应网络属性;学者武喜萍等[7]人则基于复杂网络理论对该空中交通网络的静态属性、延误传播模型、抗毁性进行了深入分析。还有诸如学者王兴隆等[8]提出了空中交通相依网络,其主要构成涉及到机场、航路和管制扇区这三大网络,并对这种相依网络的脆弱性进行了分析,将其细分成结构与功能脆弱性,分别给出了评价指标和分析方法,为解决交通系统的拥堵问题提供了改善之策。

然而上述分析研究中,研究对象仅仅只关注航空公司、机场、航路终端区或者是扇区网络,很少有考虑到网络之间的相互关系,很少有对于空中交通相依网络的研究。为此对该相依网络脆弱性进行分析研究是很有必要且迫切的,本文就是以复杂网络理论作为基础来对航路、机场和管制扇区网络以及三者叠加而成的空中交通相依网络进行研究,分析研究网络的脆弱性并给出合理的优化建议。

2 空中交通相依网络构建方法

2.1 空中交通相依网络的统计特性指标

1)相依网络节点度及度分布

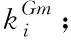
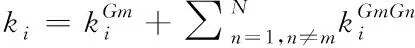
(1)

不同网络节点度分布可以用p(k)代表,表示网络中度数为k的节点数占网络总节点数的比例。

2)相依网络网络直径与平均路径长度

网络直径即网络中最短路径最长的两个节点之间所经过的边数。平均路径长度就是多层网络任意两点的最短路径均值,即

(2)

3)相依网络聚类系数

与节点i相连的节点分为在或不在同一层网络内,其连边定义为“内边”或“外边”;故相依网络聚类系数的计算公式为

(3)

2.2 空中交通相依网络构建及特性分析

空中交通相依网络是由机场网络、航路网络和管制扇区网络3个层网络构成的复杂网络,根据空中交通管理规则与航班实际运行过程,建立层网络间的逻辑连接关系,三层网络统一起来。空中交通相依网络具有多层性、多属性以及协调性等特点。

以华东地区三种网络作为例子:

图1中蓝色点表示机场节点,点的大小表示机场的全年旅客吞吐量的相对大小,绿色实线表示两机场间具有航班连通。

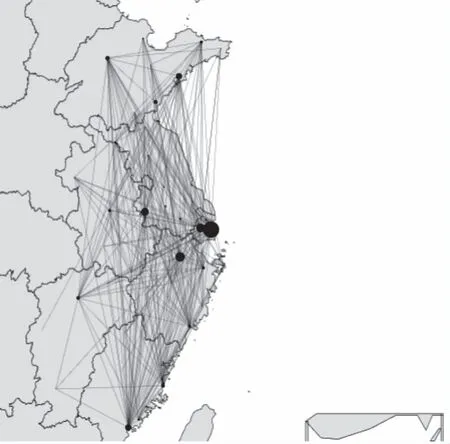
图1 华东地区机场网络

由机场网络图可以看出我国华东地区的机场分布密集,航线密集,空域复杂,且机场网络节点的度值与旅客吞吐量的大小相关,一般而言,全年旅客吞吐量越大的机场,该机场节点的度值也越大。

图2展示的为航路网络,将地面导航台当成相应的航路网络节点,不同导航台之间对应的航段实际上就是网络中的连边,由此创建相应的航路网络。

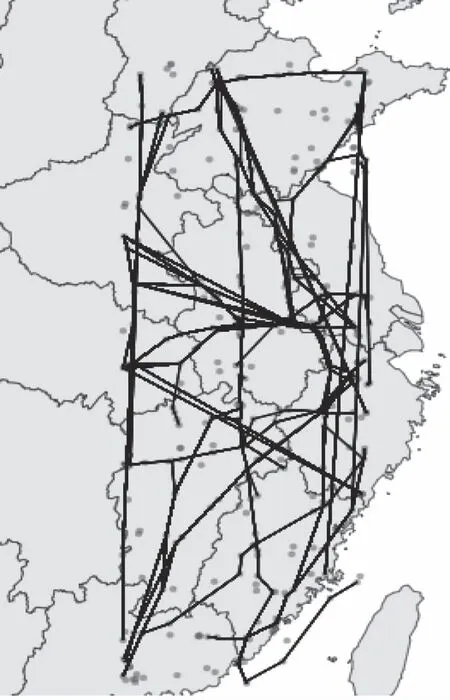
图2 华东地区航路网络

在不考虑航路的高度、形态和宽度,将节点坐标投影到二维平面中;不考虑航空器由于天气和军事活动等原因发生的改航或偏航;将航路网络视为无向网络,以我国华东地区空域航路数据为依据,建立了包含206个节点和259条边的航路网络。

根据航空器的飞行高度,我国将管制扇区划分为机场塔台管制区、终端(进近)管制区、中低空管制区和高空管制区。

为便于扇区网络的构建和分析,不考虑扇区的高度和形状,将扇区边界线投影到二维平面,扇区节点为各扇区的中心点;将扇区网络视为无向网络,即航空器起飞从机场塔台管制扇区进入终端(进近)管制扇区,继续爬升进入区域管制扇区,同样航空器降落也可沿相反路径进入机场塔台管制扇区。

本文以我国华东地区区域管制扇区数据为依据,建立了包含 57个节点,171 条边的扇区网络,如图3所示。图中蓝色实线表示扇区的实际物理边界,蓝色节点表示将区域管制扇区抽象成的节点,红色实线为扇区网络的边。

图3 华东地区扇区网络

创建空中交通相依网络模型,其中三个网络集合使用g进行表征,g={G1,G2,G3},3对层网络间边的集合为e={E12,E13,E23},则空中交通相依网络为G0={g,e},如图4所示。

图4 空中交通相依网络模型示意图

图中各连边意义如下:

1)机场网络与航路网络的连边E12即航空器从起飞阶段进入航路点以及降落阶段航空器从最后进近航路点进入机场管制区域,相应的机场节点与航路点之间的连边。

2)机场网络与管制扇区网络的连边E13即将扇区网络节点与其拥有控制指挥权的机场网络节点相连。

3)航路网络与管制扇区网络的连边E23即将管制扇区网络节点与被其控制指挥的航路网络节点相连构建连边。

3 空中交通相依网络脆弱性分析

本文在从网络内等概率的删除节点的选择性攻击和按照某种特定方法对网络节点有针对性地进行攻击的随机攻击两种方法下,计算删除不同数量节点的相依网络结构熵和网络效率;若某一层网络节点完全失效,计算终止。确定空中交通相依网络结构脆弱性算法流程如图5所示。

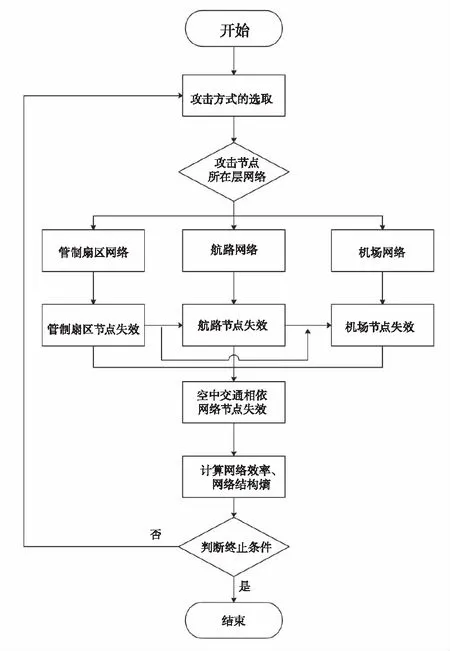
图5 空中交通相依网络脆弱性分析算法

图6 AC算法框架

在两种攻击方式下分别计算每次攻击后相依网络的网络效率和结构熵两项测度指标,每次模拟攻击重复20次取平均值,以求仿真结果的准确有效性,直到删除完网络内所有的节点。

在进行空中交通相依网络的脆弱性分析时,需提出如下三个指标:

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

1)网络结构熵

网络结构熵是对空中交通相依网络运行状态有序或无序的描述,其计算公式为:

(4)

式中N为所研究网络的节点数目,Ii为节点i的重要度,计算公式为

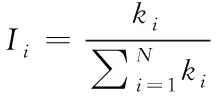
(5)

为节点i的度值。

2)网络效率

最短路径长度需要在相应连通图中加以运算,为此Latora(2001)等学者在对小世界网络模型进行研究时,引入了一个加权网络效率衡量之法[9], 其计算方法如下

(6)

式中,i至j节点最短路长度为dij,若是这两个节点之间没有连通,则dij=+∞,N为空中交通相依网络的总节点数目。

3)可达中心性算法AC值

首先定义节点间影响力为H(i,j),节点i经过长度为k的路径到节点j,其所经过的节点数量为节点i对节点j的k步路径影响力,为Hk(i,j),计算公式如下:

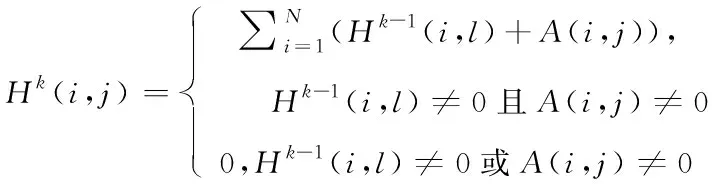
(7)

式中A(i,j)为节点i对节点j的1步路径节点间影响力,即H1(i,j)。

Hk(i,j)不仅考虑了两两节点间的连接关系,同时还考虑了两节点的路径上的节点数量,最终可使节点影响力的评估更充分合理。

节点整体影响力f(i),为节点i到网络所有节点的节点间影响力之和,当路径长度为k时,称为k步路径节点整体影响力,计算公式如下

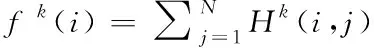
(8)

最终定义节点影响力评价指标AC(i),标等于标准化的全体k步路径节点整体影响力 与路径长度k的比值之和,计算公式如下

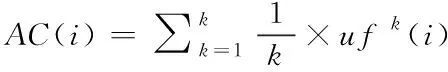
(9)

式中为的标准化处理,即

(10)

4 算例仿真

在只攻击机场网络节点时,节点通过不同层网络间的耦合机制,将影响传递至其它网络,由于部分节点失效,节点之间的连接被破坏,连边减少,网络的连通性变差,节点间的距离变大,相依网络的效率会降低。按照节点的聚类系数优先的攻击方式,首先将网络中连接紧密的机场先删除,因此小机场被删除的概率较大,最终导致对网络效率的影响较缓慢。如图7所示。

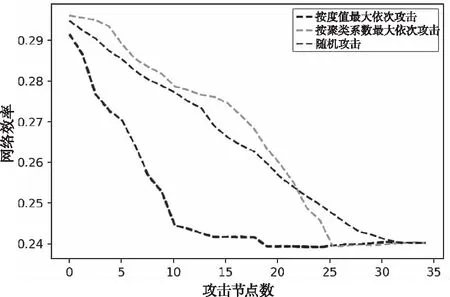
图7 不同攻击方法攻击机场网络节点,网络效率变化

由图8可得,攻击航路网络节点后,网络效率先降后增,采用不同的攻击方法攻击航路网络节点,网络效率的变化差异性更大。当删除网络50%-70%的节点时,网络效率呈现出了不降反增的情况,原因在于一部分航路点被删除后,各层网络间的连边数量也减少,机场网络和扇区网络之间的距离因为航路节点的删除而变小,网络节点数变少,网络的连通性变大,网络效率变大。

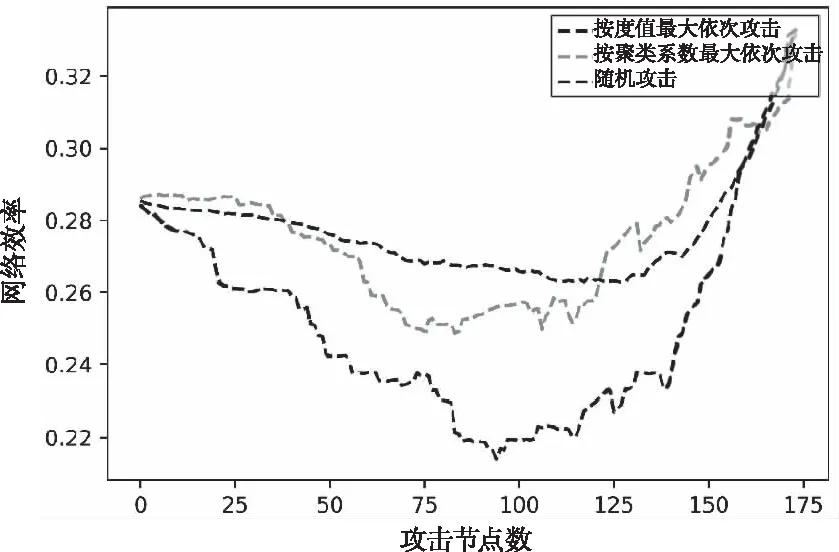
图8 不同攻击方法攻击航路网络节点,网络效率变化

如图9,用度值最大依次攻击的攻击方法,在删掉某扇区节点时,网络效率急剧降低,说明该扇区节点在相依网络的连通上起关键性作用。当删除网络大约80%的节点时,网络效率维持在最低值,说明此时网络中的节点大多数为孤立的,网络的连通性极差,再删除节点对网络的路径长度影响不大,网络处于近乎崩溃的状态。

图9 不同攻击方法攻击扇区网络节点,网络效率变化

在基于网络结构熵的算例中,如图10所示,网络结构熵先升后降,这是由于当攻击度值较大的机场时,并没有使得网络的脆弱性变得显著,网络结构熵暂时增大,相依网络由有序向无序状态变化,节点的度分布差异变大;随着攻击节点数的增加,网络结构熵开始下降,此时网络的节点度分布近似,相依网络向有序状态变化。

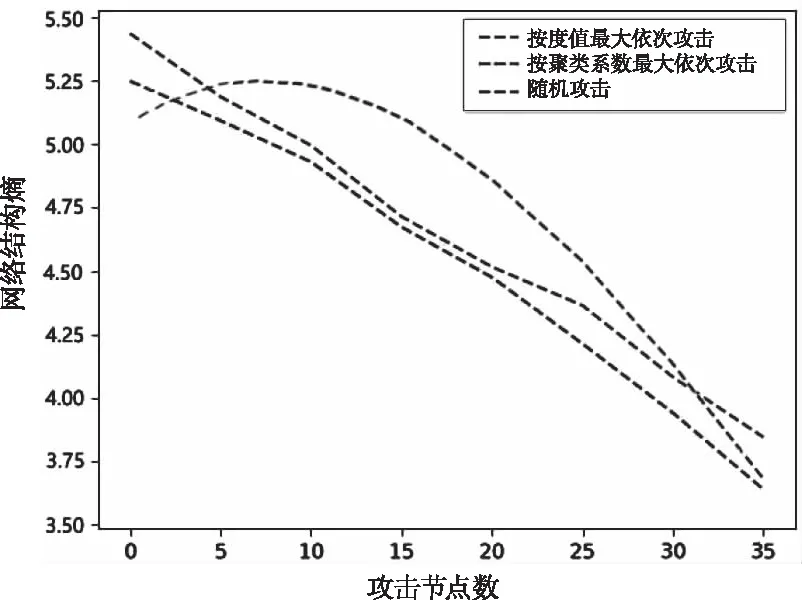
图10 不同攻击方法攻击机场网络节点,网络结构熵变化

当采用聚类系数最大依次攻击和随机攻击攻击网络节点时,网络结构熵均是呈下降趋势。

采用选择性攻击和随机攻击对航路网络和扇区网络节点进行攻击时,如图11和图12所示,网络结构熵均为均匀下降的趋势。随着航路节点和扇区节点的删除,空中交通相依网络由无序状态转变为有序状态,网络节点的度分布差异性也降低,机场网络、航路网络和扇区网络之间的连接失效,连边减少,相依网络被分解为诸多小型网络,网络的连通性降低。

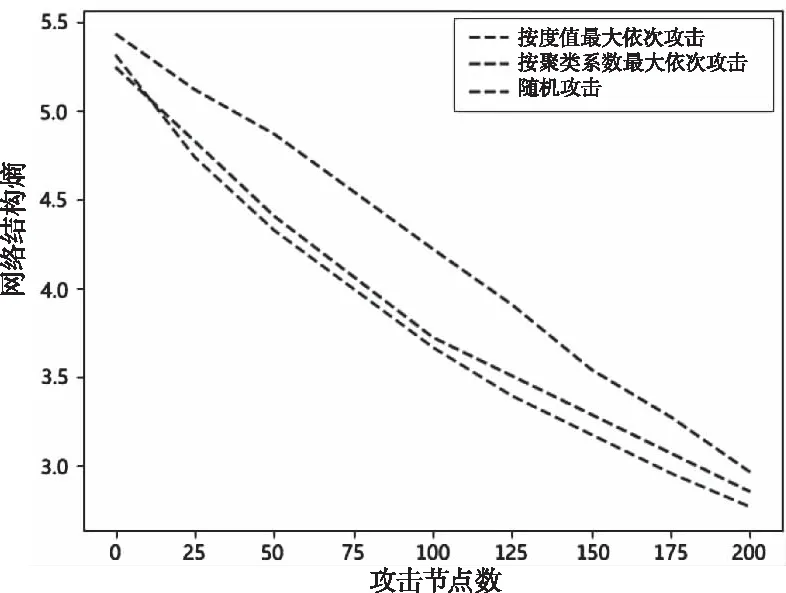
图11 不同攻击方法攻击航路网络节点,网络结构熵变化

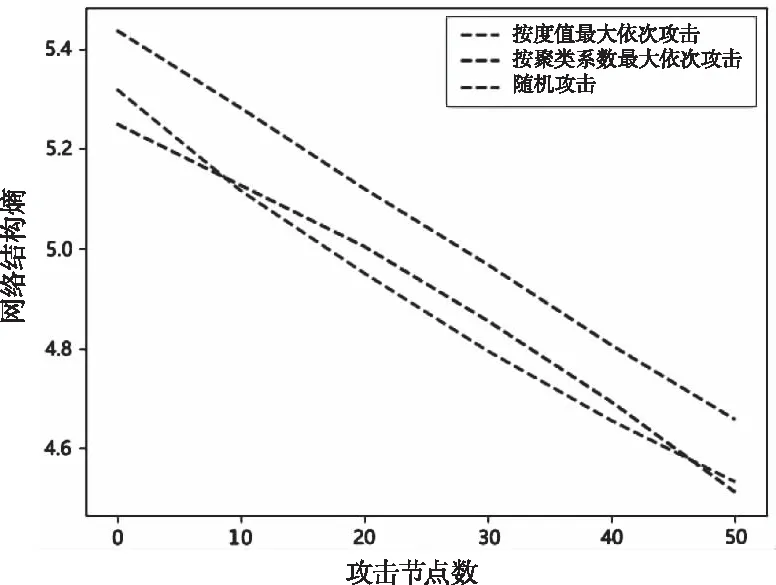
图12 不同攻击方法攻击扇区网络节点,网络结构熵变化

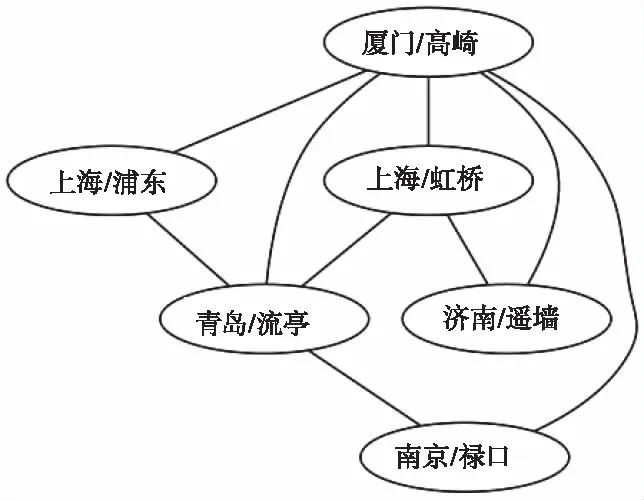
图13 华东地区部分机场网络拓扑模型

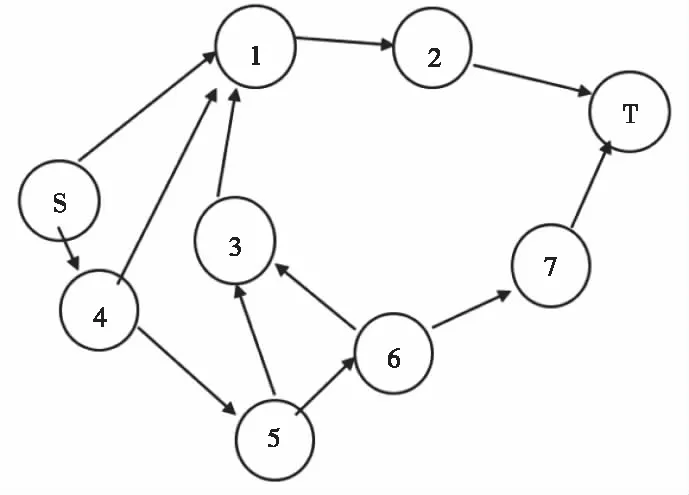
图14 天河VOR-浦东VOR航路网络拓扑模型

在实例分析中,选取了华东地区几个典型机场进行拓扑网络建模,同时,也对华东地区航图的航路进行拓扑网络建模,构建图分别如下。

其中S为天河VOR、1为合肥VOR、2为无锡VOR、3为浠水VOR、4为龙口VOR、5为向塘VOR、6为景德镇VOR、7为桐庐VOR、T为浦东VOR。

根据上述AC算法的计算流程,得到每个节点的AC值,即每个机场节点与航路节点的全局影响力,结果如表1、表2所示。

表1 AC算法的机场节点影响力计算结果

表2 AC算法的航路节点影响力计算结果

由表中结果可得,在此网络中厦门/高崎机场的AC值最大,节点影响力最大,说明厦门/高崎机场为网络的重要节点,破坏此节点,可能会引发网络的脆弱性。

由表中结果可得,在此航路网络中合肥VOR的AC值最大,节点影响力最大,说明合肥VOR此航路点为网络的重要节点,破坏此节点,可能会引发网络的脆弱性,造成航班改航。

5 结论

本文基于复杂网络基础理论,分析了空中交通相依网络的动态脆弱性,研究成果如下:

1)确定评估指标为网络效率和网络结构熵,采取选择性攻击和随机攻击两种方法进行算法仿真,研究相依网络脆弱性的影响与变化。

2)引入可达中心性算法,在考虑网络拓扑结构的影响下,识别相依网络的重要节点,以实现预战略角度的先期流量管理。

然而,本文的研究还有很多待完善之处。例如,在本文的研究中,删除网络节点时,没有考虑到实际运行过程中节点被破坏对运行的影响;在进行脆弱性分析时,没有确定评估指标的重要程度、各指标的影响程度大小,以及如何定量的评估网络的脆弱性都没有分析;故而未来的研究将继续深入和优化。