机载微型导弹动基座传递对准方法研究
2023-09-03杨光鑫刘玉祥樊世兵陈中祥
王 伟,杨光鑫,刘玉祥,樊世兵,任 韦,陈中祥
(江南机电设计研究所, 贵阳 550009)
0 引言
随着世界局势的快速剧烈变化,当前战争的主要模式已经迅速演变为局部的城市巷战、反恐维稳处突和边境封控等非对称作战[1]。在这些作战场景中,采用轻小型无人机+低成本微型导弹,实现侦察打击一体化、发现即打击,是控制交战规模、减小附带损伤、增强作战灵活性、提升作战效能、节约战争经费的最佳选择之一。微型导弹从无人机平台发射时,弹上惯性设备需要进行传递对准,才能准确获得初始装订信息,以便为后续安全发射及目标精确打击奠定基础。
传递对准方法根据主、子惯性导航系统所选量测匹配量的不同,可以分为计算参数匹配、量测参数匹配和混合参数匹配3类[2-3]。当前工程应用中较为成熟的方法包括速度匹配、位置匹配、速度+姿态匹配、速度+角速率匹配等,传递对准的快速性和精确性均满足传统空基导弹的需要[4- 5]。但是,上述方法并不适合机载微型导弹,主要原因是微型导弹的几何尺寸小(弹径不大于70 mm)、全弹质量轻(不超过5 kg)、成本限制严格,不具备安装高性能信息处理器的条件,只能使用微型低成本弹载机,计算能力非常有限,不能满足常规传递对准方法的计算资源需求,无法实现传递对准。目前,针对微型导弹机载平台应用的研究较少,动基座传递对准方法相关研究更少,限制了相关轻小型察打一体无人装备的研制及应用[6-10]。
为此,本文中首先根据轻小型无人机和低成本微型导弹的特点,确定适合的传递对准匹配方法,并建立对应数学模型;然后通过数值仿真方式,对匹配方法有效性进行验证,最后给出结论。
1 机载微型导弹传递对准方法分析
根据中国民航局[11]对无人机的分类标准,轻小型无人机的起飞重量不大于25 kg、最大飞行速度不超过50 m/s,具有飞行速度慢、机动能力弱的显著特征,因此,机载微型导弹不适合采用速度匹配和位置匹配法;姿态匹配、角速率匹配方法应用于大中型飞行器时,由于角运动量测值变化速率快等影响,必须复合速度等其他量测值,才能满足对准要求。考虑轻小型无人机的姿态变化不明显,并且单量测值对准方法所需计算资源较小,比较适合机载微型导弹使用。而在角运动量测方法中,姿态匹配法比角速率匹配法的对准精度更高,抗干扰能力更强,更有利于遂行目标精确打击任务。因此,采用姿态匹配方法,进行机载微型导弹传递对准。
传统的姿态匹配法,处理的通常都是大角度姿态信息,应用于轻小型无人机+微型导弹时,需要进行适应性的修正才能实现传递对准,即轻小型无人机机载惯导设备(主惯导)、微型机载导弹惯导设备(子惯导)分别完成姿态角、海拔高度等导航参数获取后,需要增加进行姿态矩阵小角度变化提取环节,才能保证量测方程小角度线性特征,改进后的工作原理如图1所示。
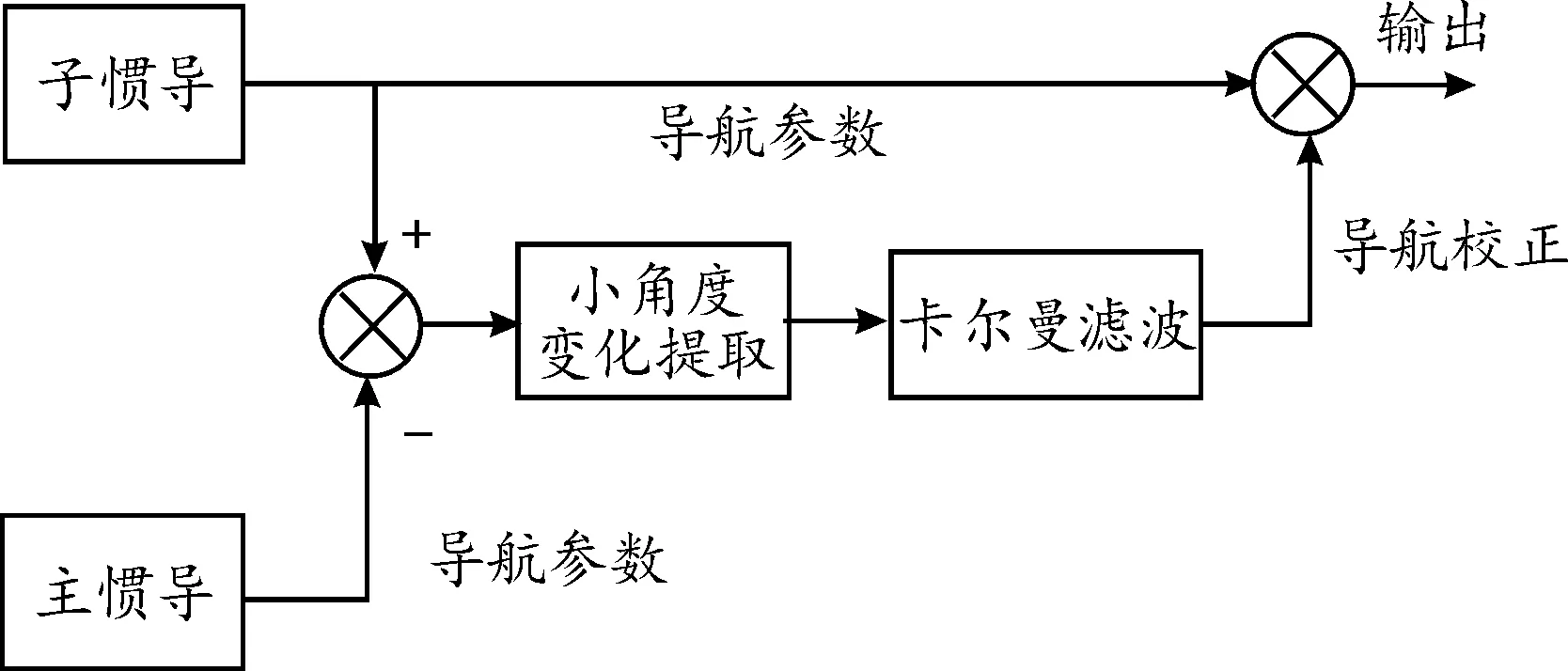
图1 基于姿态匹配的传递对准原理
机载微型导弹姿态匹配修正方法数学模型,包括姿态误差方程、姿态矩阵匹配方程、姿态矩阵小角度提取和传递对准滤波器设计4部分。
1.1 姿态误差方程

(1)
忽略旋转矩阵二阶小量,可得到
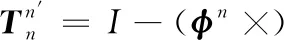
(2)
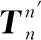
因此,子惯导系统姿态阵的误差为

(3)


(4)
式中:上标s表示在s坐标系下向量分量,下标is表示在s坐标系相对于i坐标系的角速度。
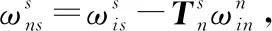

(5)
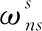

(6)

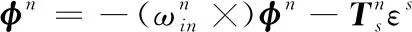
(7)
1.2 姿态矩阵匹配方程

(8)
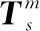

(9)
将式(8)代入式(10)中,得

(10)
式中:φn×为φn向量构成的反对称矩阵,Λ×为安装角误差Λ(ψx,ψy,ψz)构成的反对称矩阵。
忽略上式中的二阶小量,可得到:
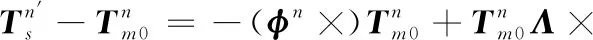
(11)
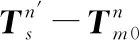
Z=H[φx,φy,φz,ψx,ψy,ψz]T+v
(12)
1.3 姿态矩阵小角度提取
采用姿态匹配方法时,其状态方程的维度为6维,包括3个失准角和3个安装误差角,即:
X=[φx,φy,φz,ψx,ψy,ψz]T
(13)
此时,传递对准状态方程为

(14)

整理得到的传递对准量测方程如下:
Z(t)=H(t)X(t)+v(t)
(15)


(16)
1.4 传递对准滤波器设计
将式(14)、式(15)联立,组成连续传递对准系统方程。假设一个滤波周期内状态方程和量测方程矩阵变化幅度较小,捷联式惯导系统可近似为定常系统。据此,将姿态方程和量测方程离散化,得

(17)
式中:Θk,k-1为状态转移矩阵,Γk-1为噪声驱动矩阵,数学表达式分别如下:
结合噪声统计特性确定的陀螺测量噪声矩阵Qk和量测噪声方差阵Rk,利用离散化卡尔曼滤波方程,即可完成捷联导航误差角估计,如图2所示。

图2 卡尔曼滤波流程图
2 姿态匹配修正方法数值验证
为了验证前文姿态匹配修正方法的正确性,采用数值仿真方法进行验证,判定条件根据实际应用需求确定为:估计时间不大于10 s,并且失准角和安装角估计精度不大于5′。
2.1 仿真条件
假设无人机处于悬停状态,过载机动选择分时进行。在上述设计原则下,根据预先设定的工作环境,选择3种仿真条件共9种工况:
1) 相同机动、不同安装角。
无人机悬停后,沿机体坐标系3个轴分别作周期为3 s、幅值为10°的正弦机动;子惯导相对于主惯导轴向安装误差角为[10′,40′,-80′];子惯导陀螺采样周期和滤波周期分别为2.5 ms和20 ms;滤波器状态初值为06×1;估计误差均方差初值P(0)、系统噪声方差阵Q、量测噪声方差阵R分别为
机载微型导弹相对无人机的安装角,分别为:
工况1:安装角(-1°,2°,0°);
工况2:安装角(-1°,3°,180°);
工况3:安装角(-1°,3°,-175°)。
2) 相同安装角,不同机动。
机载微型导弹相对无人机的安装角为(-1°,3°,180°);无人机悬停后,机动方式分别为:
工况4:沿无人机坐标系x轴作周期为3 s、幅值为10°的正弦机动;
工况5:沿无人机坐标系x和y轴分别作周期为3 s、幅值为10°的正弦机动;
工况6:沿无人机坐标系x、y和z轴分别作周期为3 s、幅值为10°的正弦机动。
3) 相同机动、安装角,不同安装误差。
机载微型导弹相对无人机的安装角为(-1°,3°,180°);无人机悬停后,分别沿坐标系x、y和z轴作周期为3 s、幅值为10°的正弦机动;子惯导相对于主惯导轴向安装误差角分别为
工况7:[50′,30′,80′];
工况8:[-50′,-40′,80′];
工况9:[50′,40′,-80′]。
2.2 仿真结果及分析
图3、图4分别给出了典型工况下,得到的失准角和安装角变化曲线,其中横坐标为时间(s)、纵坐标为角度估算值(′),图中红线为x方向值、蓝线为y方向值、绿线为z方向值。可以看出:分别沿机体坐标系3个轴作总共9 s的正弦机动后,失准角和安装角均快速收敛,并且二者变化趋势基本一致。

图3 失准角(工况1)
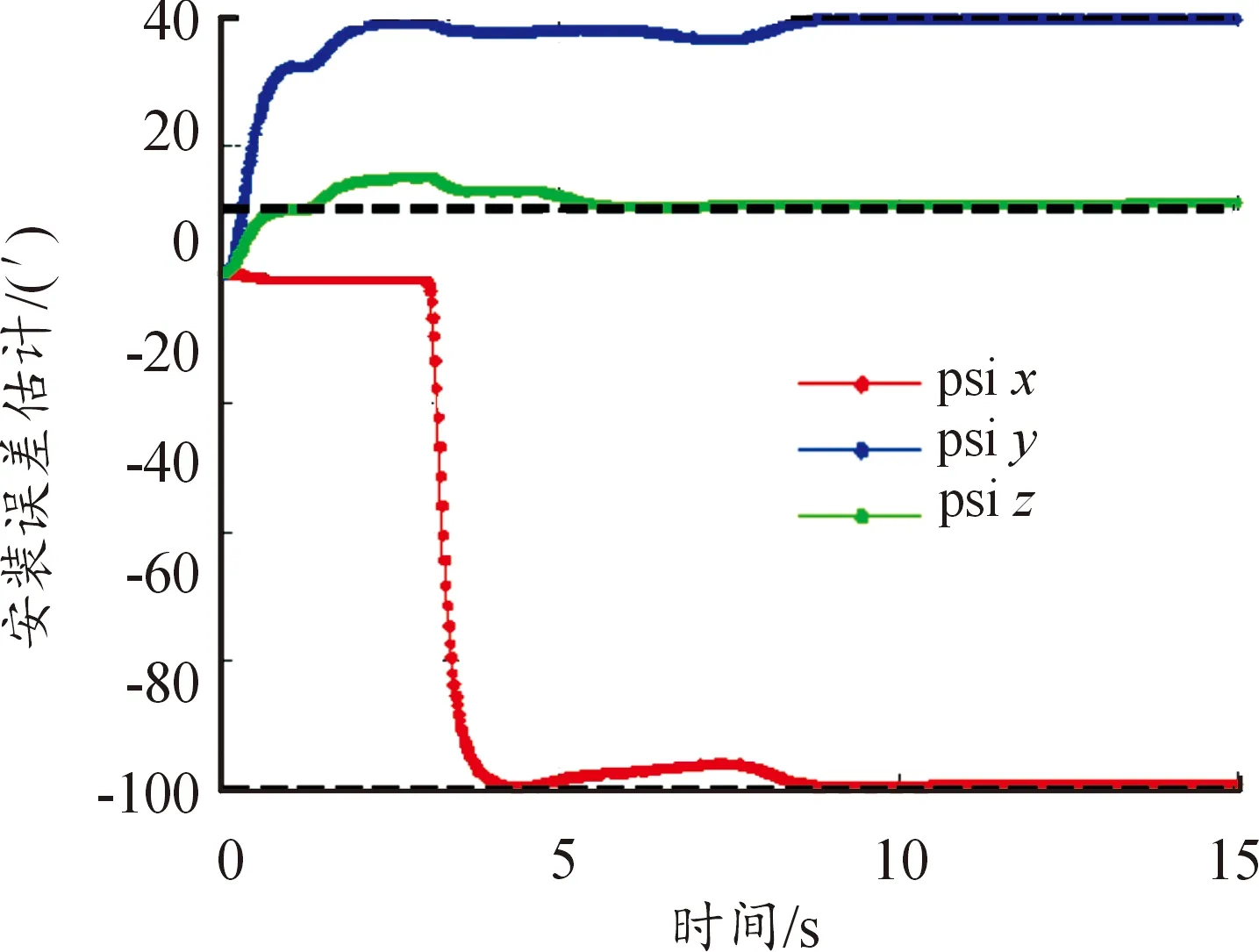
图4 安装角(工况1)
图5、图6给出了上述工况下,得到的失准角和安装角误差变化曲线,可以看出:失准角的最大估算误差在2.5′左右,安装角的最大估算误差约为0.8′,估算精度较好。
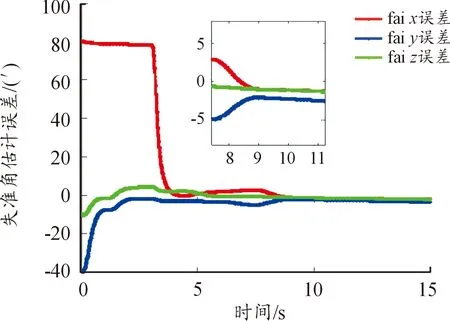
图5 失准角估计误差(工况1)

图6 安装角估计误差(工况1)
鉴于失准角和安装角的估算具有相似变化规律,以下只进行失准角分析。图7、图8分别给出了工况2、工况3的失准角变化曲线。可以看出:设定工况下,失准角估计时间都在9 s左右,估算误差约为3.8′。结合图5可知,在机动方式相同、不同安装角条件下,姿态矩阵匹配修正方法均能在10 s内完成失准角、安装角误差估计,并且估计精度均小于5′。

图7 失准角估计误差(工况2)

图8 失准角估计误差(工况3)
图9给出了工况4的失准角变化曲线。可以看出:沿无人机坐标系x轴作设定正弦机动时,x方向失准角估计时间大于10 s,这说明基于姿态匹配修正的传递对准方法,在无人机做单轴摇摆机动条件下不能完成失准角的有效估计。

图9 失准角估计误差(工况4)
图10、图11分别给出了工况5、工况6的失准角变化曲线。可以看出:沿无人机坐标系作双轴或者三轴分时姿态摇摆机动时,姿态矩阵匹配修正方法都能实现对失准角误差的有效估计,并且收敛时间基本一致(约为9 s)、估计精度在4′左右。
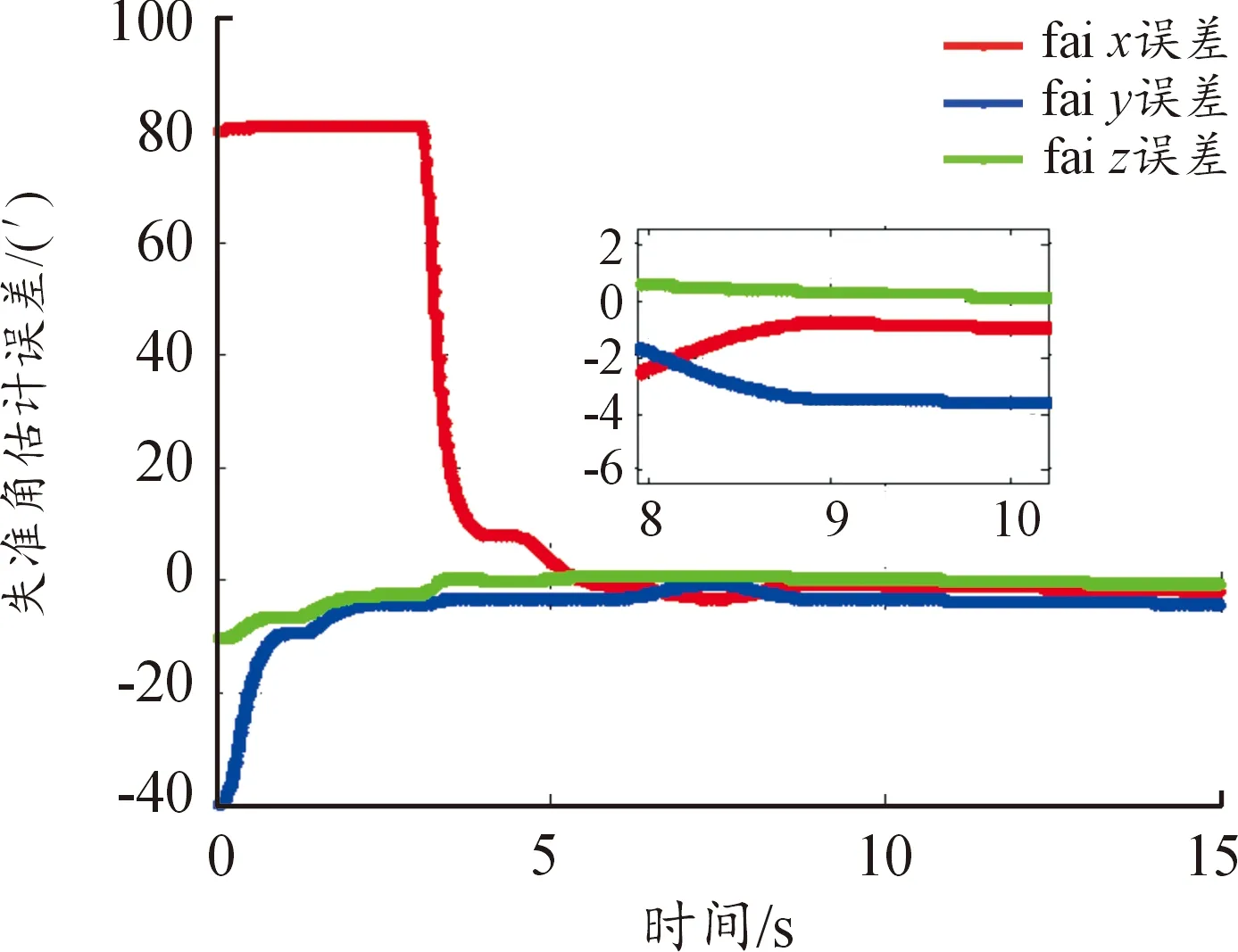
图10 失准角估计误差(工况5)

图11 失准角估计误差(工况6)
图12—图14分别给出了三轴分时摇摆、相同安装角、不同安装误差条件下失准角变化曲线。可以看出,3种工况下,姿态矩阵匹配修正方法的估算时间均在9 s左右、估算误差约为4′。

图12 失准角估计误差(工况7)

图13 失准角估计误差(工况8)

图14 失准角估计误差(工况9)
3 结论
根据轻小型无人机和微型导弹的特点,分析确定了基于姿态匹配修正的传递对准方法,构建了相应的数学模型,并完成了仿真验证。通过研究,可以得出以下结论:
1) 采用基于姿态匹配修正的传递对准方法,可以有效解决微型导弹应用于轻小型无人机平台的动基座传递对准难题,为后续相关装备研制奠定了良好基础。
2) 基于姿态匹配修正的传递对准方法,在无人机做双轴分时或三轴分时摇摆机动时均能完成失准角、安装角误差的估计。
3) 本文设定条件下,失准角及安装角误差估计误差均在5′以内,收敛时间不大于10 s。
