大型装备航空运输装载规划优化方法

赵 灿,吴 磊,张 帅

(1.陆军工程大学训练基地, 江苏 徐州 221004; 2.空军勤务学院, 江苏 徐州 221000)

0 引言

在保障抢险救灾等紧急任务时需要一次性投送多型号多台次大型装备,在装载前需针对不同运输投送任务进行装载方案规划,而装载方案直接影响航空投送效率。为保证货运飞机飞行安全的前提条件下尽可能提高航空运输的效率,需综合分析运输机的载重、重心平衡和空间约束,使得各项参数处于安全许可范围内,保证装载安全,同时尽可能利用最少架次运输机完成一次投送任务。

目前,关于航空装载方案规划问题可简化为带有约束的装箱问题[1]或背包问题[2],针对不同应用场景建立一维、二维或三维矩形物体布局模型[3],是典型的NP-hard问题[2],求解方法包括图论法、模拟退火算法、遗传算法、禁忌搜索算法[4]、数学规划法[5]等。孟冲等[6]将空间布局约束转换成0～1整数线性规划,实现对0～1整数线性规划空运装载问题的求解;Bertsimas等[7]提出了在诸多限制条件下利用混合整数规划模型解决美军人员和货物以最小延迟和最大可用飞机利用率交付需求为目标的空运规划问题;Roesener 等[4,8]针对货物装载在最少数量的空运飞机问题,提出了禁忌邻域搜索算法求解混合有效载荷空运装载问题和动态空运装载问题;海军等[9]以军用运输机装载质量最大、空间利用率最高作为优化目标建立多目标优化模型,利用蚁群算法进行求解;陈丙成等[10]主要将精英选择策略的精英遗传算法与轮盘赌的简单遗传算法相结合,用于装箱问题求解;刘胜等[11]提出了一种启发式正交二叉树搜索算法用于三维装箱问题的求解;李建等[12]针对大规模同时集散货物路线问题,提出了一种集成大量邻域搜索方法的禁忌搜索算法,用于提高求解能力。

目前针对尺寸较小、单体质量较轻物体的航空运输装载优化及优化算法本身相关问题研究较多,并取得了很好的研究成果。但大型装备具有单装尺寸大、吨位重,同时不同机型货舱的不同区域地板的设计承重强度不同[13],装备装载位置对于运输机安全性有直接影响,专门针对大型装备特点进行的相关研究较少。

前期通过与空军勤务学院合作开展了关于单台大型装备空运适应性的理论研究、虚拟仿真和装载试验,该项成果确保了用于装载优化问题研究的大型装备均可用运输机进行装载运输。为确保运输机安全,结合大型装备的特点,在综合考虑了运输机装载大型装备总重限制、空间限制、平衡制约基础上,增加了对运输机地板分区载重约束的考虑,以完成单次运输任务所需最少运输机为优化目标,建立了大型装备军事航空运输装载优化模型。航空运输装载优化属于NP-hard问题,用启发式算法求解该类问题较为合适[4]。

1 装载优化模型建立

现需要使用货运飞机将一批大型装备通过航空运输部署到任务区,待运输工程装备型号、数量及相关运输性参数已知。运输机的货舱有效长、宽、高,空载重量,空载满油重心位置,总载重量均已知。另外,如图1所示,可用于大型装备装载的运输机货舱有A、B、C、D等4个分区,每个分区的总载重量、长度已知。

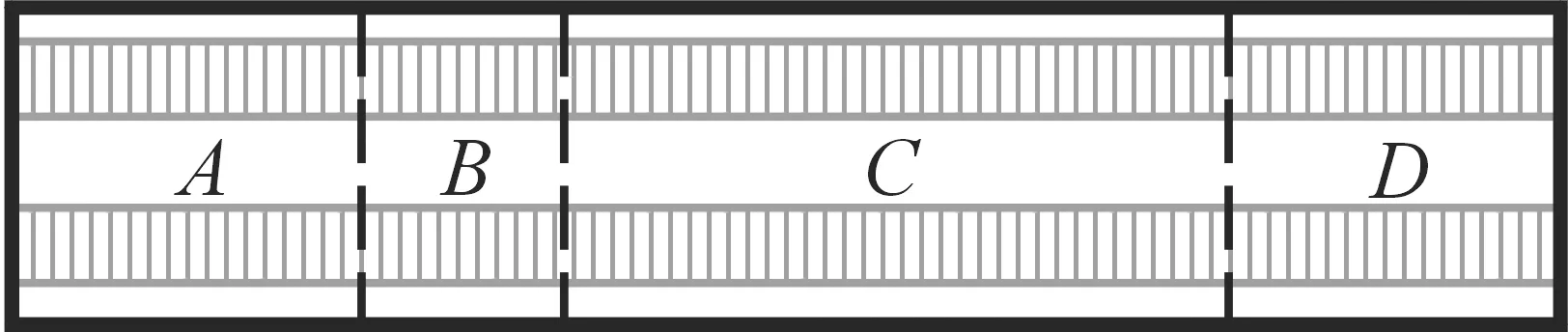
图1 运输机货舱ABCD 4个分区示意图

为了便于使用运输机的重心限制图进行运输机重心计算,建立运输机的货舱直角坐标系。坐标系原点O位于货舱前部,沿运输机纵向中轴线为X轴,由机头向机尾方向为正方向,沿运输机的横轴方向为Y轴,沿运输机的立轴方向为Z轴。货舱直角坐标系,如图2所示。由于装备的装载是由内向外,先进入货舱的装备在内,后进入货舱的装备在外,装备沿X轴线正方向排列。因此装备的位置可用该装备最左端在X轴的位置表示。

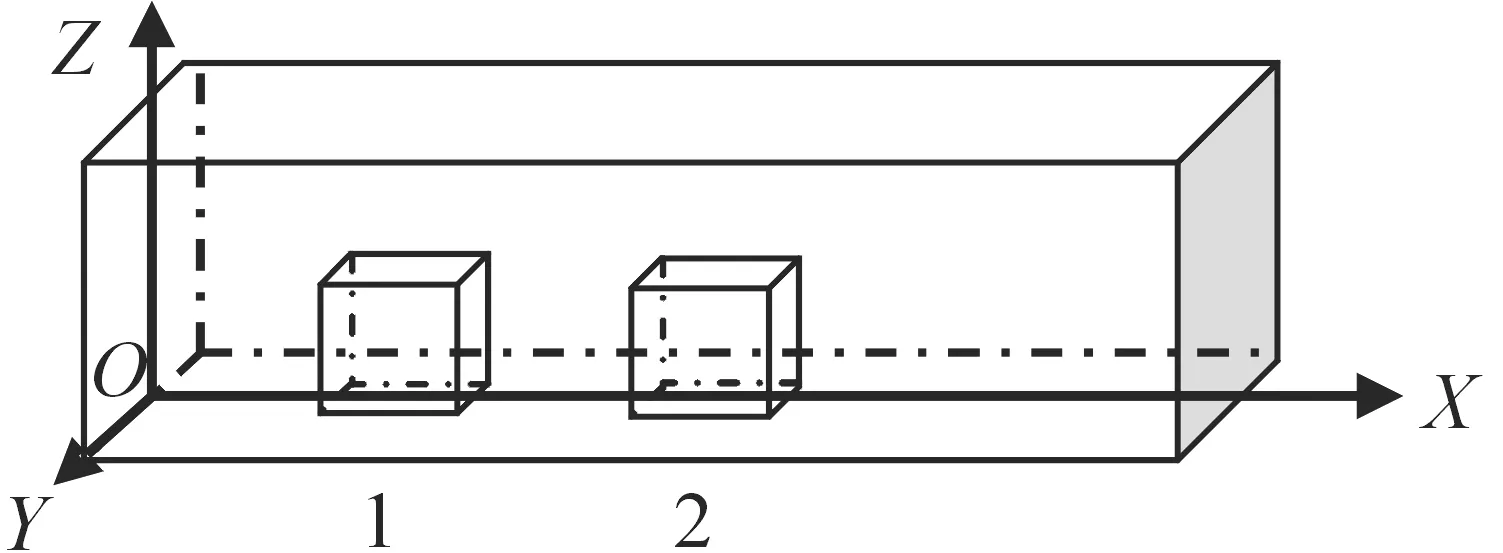
图2 货舱直角坐标系

1.1 模型假设

基于前期对大型装备空运适应性研究成果,为了便于模型构建,对不规则的运输机货舱内部空间、不规则的大型装备外形轮廓进行简化。

1) 大型运输机货舱的横截面并不是规则的圆形或矩形,为了便于建模计算,将运输机货舱的可用装载空间简化为长方体,如图2所示。

2) 大型装备形态各异,外形不规则,将待运大型装备最大外形轮廓简化为长方体[13],将不同装备处于装载时姿态的实际重心作为装备模型重心。

3) 假设所有待装载大型装备可以任意装载在若干架次运载飞机货舱内。

4) 大型装备由于尺寸较大,难以横向摆放或横向摆放后难以转向。因此,假设待装载大型装备只能沿X轴线摆放。

5) 待运大型装备不可以层叠摆放。

6) 待运大型装备优先装载在运输机货舱的某个分区中,当大型装备长度超过某一货舱分区长度时,可以占用相邻2个或3个分区。

7) 考虑到只有紧凑排列才能使运输机货舱被占用长度最小,因此假设同一机舱内的所有装备紧凑排列,任意相邻2台装备系留间距为国军标[14]规定的最小间距300 mm。

1.2 优化模型

以使用最少数量的运输机为优化目标,将一批次各型装备合理地装到运输机上,以提高投送效率,约束条件包括:重心位置约束、飞机总载重量约束、空间约束、飞机分区载重约束[15],以此建立运输装载优化模型,有

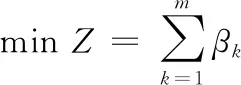
(1)

s.t.Xmin(k)≤Xk≤Xmax(k)

(2)

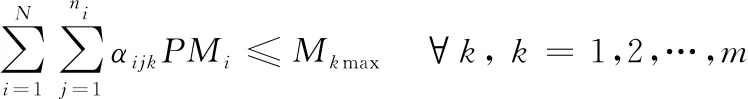
(3)

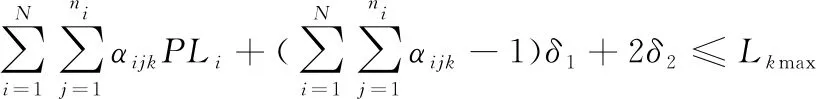
(4)

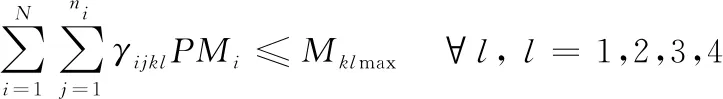
(5)

式(1)—(5)中:βk表示当第k架次运输机Fk装载装备的决策变量,当装载时βk=1,否则βk=0;Xk表示第k架次运输机装载后的重心坐标,Xmin(k),Xmax(k)分别表示第k架次运输机最小,最大重心坐标位置;P={Pi|i=1,2,…,N}={pij|pij∈Pi;i=1,2,…,N,J=1,2,…,ni}表示待运装备集合,其中N为待运装备的种类数,i为集合中装备的种类号,ni为第i类装备的总辆数,j为某类装备中的件数号;αijk表示当运输机Fk装载装备pij的决策变量,当装载时αijk=1,否则为αijk=0;PMi、PLi分别表示第i类装备的质量和长度,i=1,2,…,N;δ1为装载后相邻2台装备之间的最小距离,δ2为装载后所运装备、物资的顶部或四周与飞机内部结构之间的最小间隙;Mkmax、Lkmax、Mklmax分别表示第k架运输机可用于装载的最大载重量、最大机身长度、第l分区最大载重量。

2 算法设计

2.1 初始解获取

通过随机搜索算法获取一个初始解。具体步骤如下:

步骤1数据初始化:输入运输机与待运装备基本参数。

步骤2终止条件:迭代N次,且之后某次所用运输机数量小于前面计算的各次,则终止,得到一个可行解。否则,继续步骤3。

步骤3将所有型号的所有待运装备编号,随机排列得到一个装备编号序列。

步骤4利用货舱长度、载重约束,分割装备子序列,得到初步装机方案。

步骤5利用货舱长度约束,计算每架运输机上装备子序列的重心范围。

步骤6装备子序列的重心范围与运输机重心可用范围有交集,则继续第7步。否则,终止本次搜索,返回步骤2。

步骤7取交集,得到每架运输机上装备子序列的实际重心范围与装备首部(最左端)坐标。

步骤8校核运输机地板分区最大载重约束,如满足,则记录所用装载方案;否则,终止本次搜索,返回步骤2。

2.2 禁忌搜索算法

禁忌搜索算法可用于解决组合优化问题,由于采用类似于人类记忆功能的禁忌策略,容易跳出局部最优。当某些搜索策略或搜索区域适应值较好,可能在没被禁止到一定周期就解除禁忌,这称为藐视条件,更容易搜索到全局最优。禁忌搜索算法的步骤不再赘述。算法流程如图3所示。

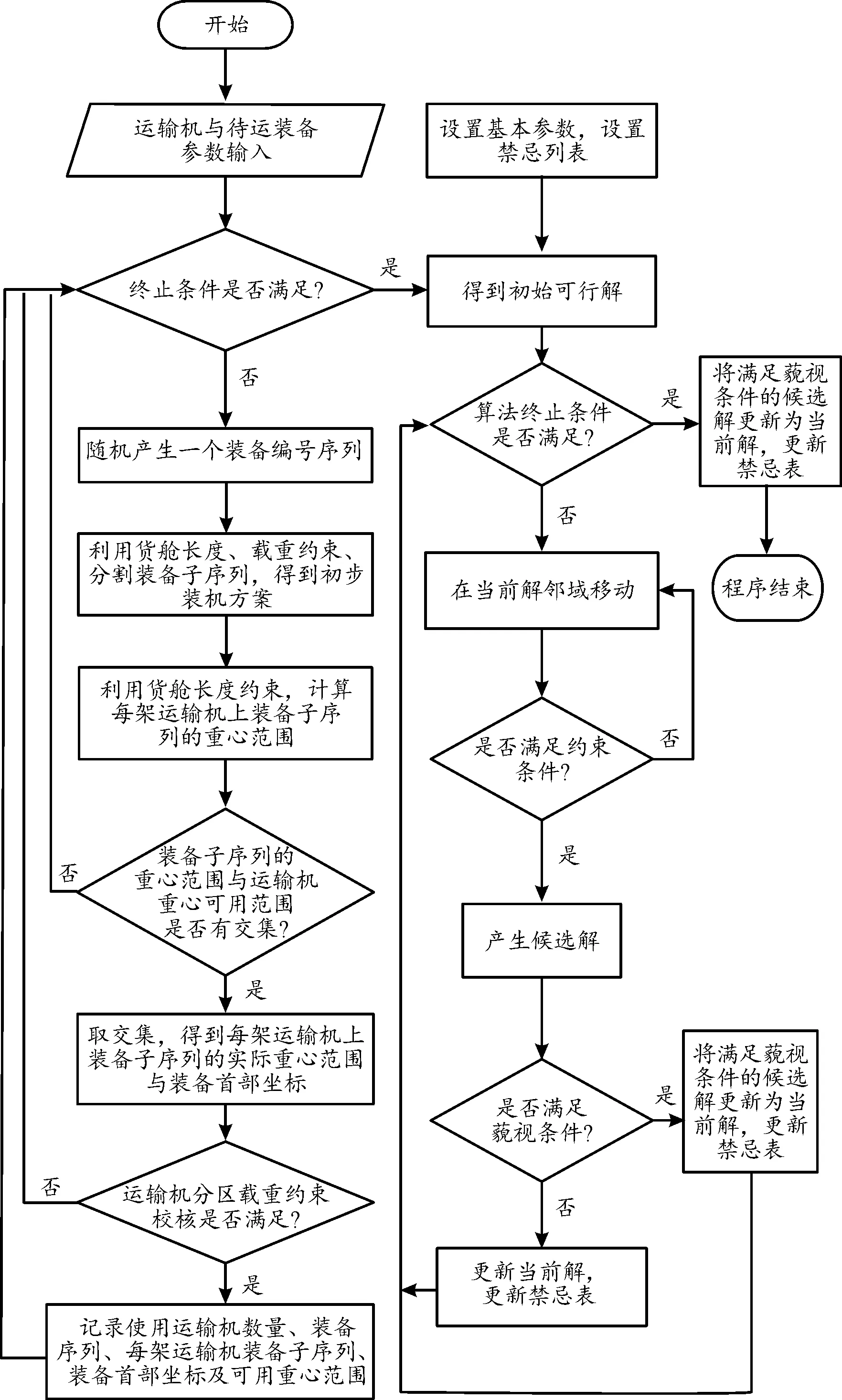
图3 算法流程图

2.3 禁忌搜索算法要素的确定

用禁忌搜索算法求解大型装备航空运输装载优化问题,需要确定解的表示、解的评价、邻域点产生方法、算法终止准则、禁忌对象、禁忌长度及候选集等要素[16]。

采用将待运大型装备直接排列的表示方法,即将所有类型待运的装备按照一定的顺序直接排列成为一个序列,并对其连续编号。这个自然数数列就构成了一个解,并对应了一种装载方案。邻域点产生方法采用两换位法,产生若干个邻域点,指定迭代步数作为算法终止准则,采用解的简单变化作为禁忌对象,以待运装备数量作为禁忌长度,邻域中随机选择若干评价值较好的邻居作为候选集。

3 数值计算

程序设计利用模块化思想,对主要功能函数进行封装,以便于修改、调试与调用。程序主要包括装备与运输机运输性数据读取模块、运输机货舱总长度与总重量约束计算模块、运输机重心范围约束计算模块、运输机分区载重约束计算模块、禁忌搜索算法模块以及结果分析呈现模块。利用MATLAB软件编程,对装备航空运输装载方案优化进行计算,得出最优解。

某次远程投送任务待装载的装备为9型15台装备,型号用字母代替如表1所示。

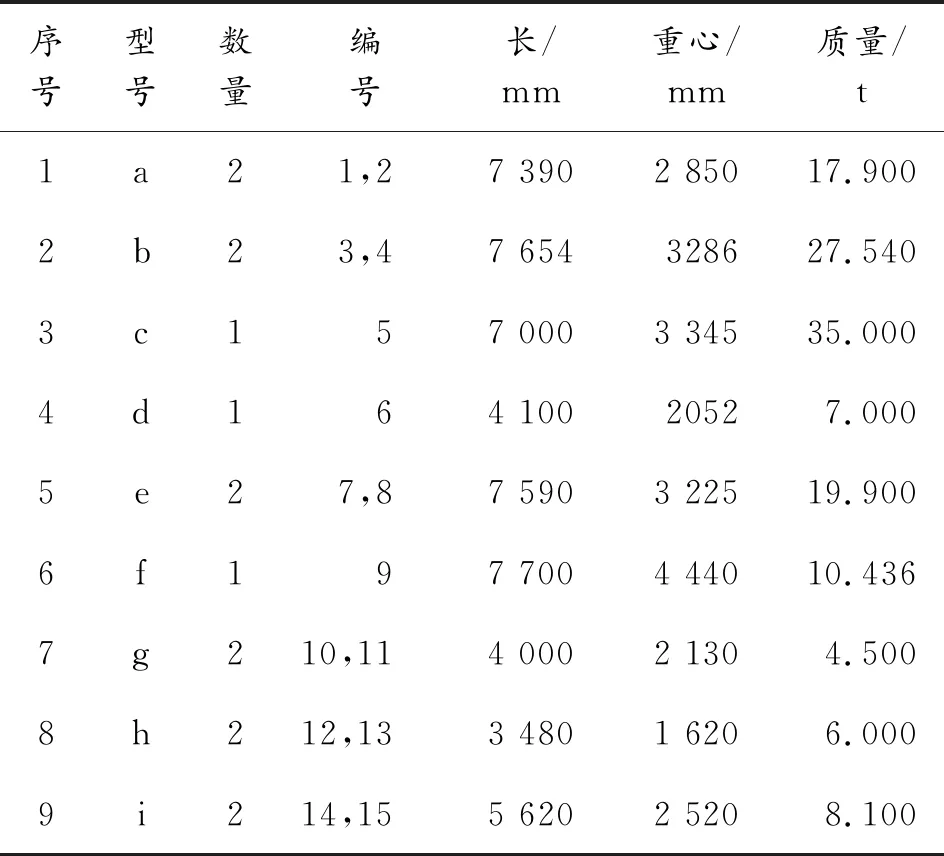
表1 待运装备型号、数量等相关参数

利用所建立的优化算法可计算得出装载方案,结果显示,使用6架次货运飞机即可完成此次装备投送装载任务,6架次货运飞机装载的装备型号分布如表2所示。待运装备在各架次运输机的位置,相对于货舱前部的坐标如表3所示。待运装备的装载方案图如图4所示。

表2 待运装备型号分布

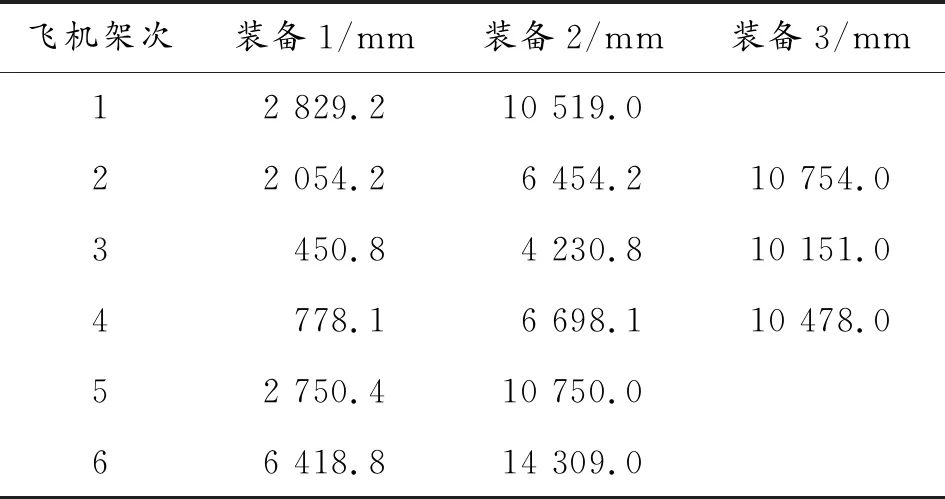
表3 待运装备相对于货舱前部X坐标

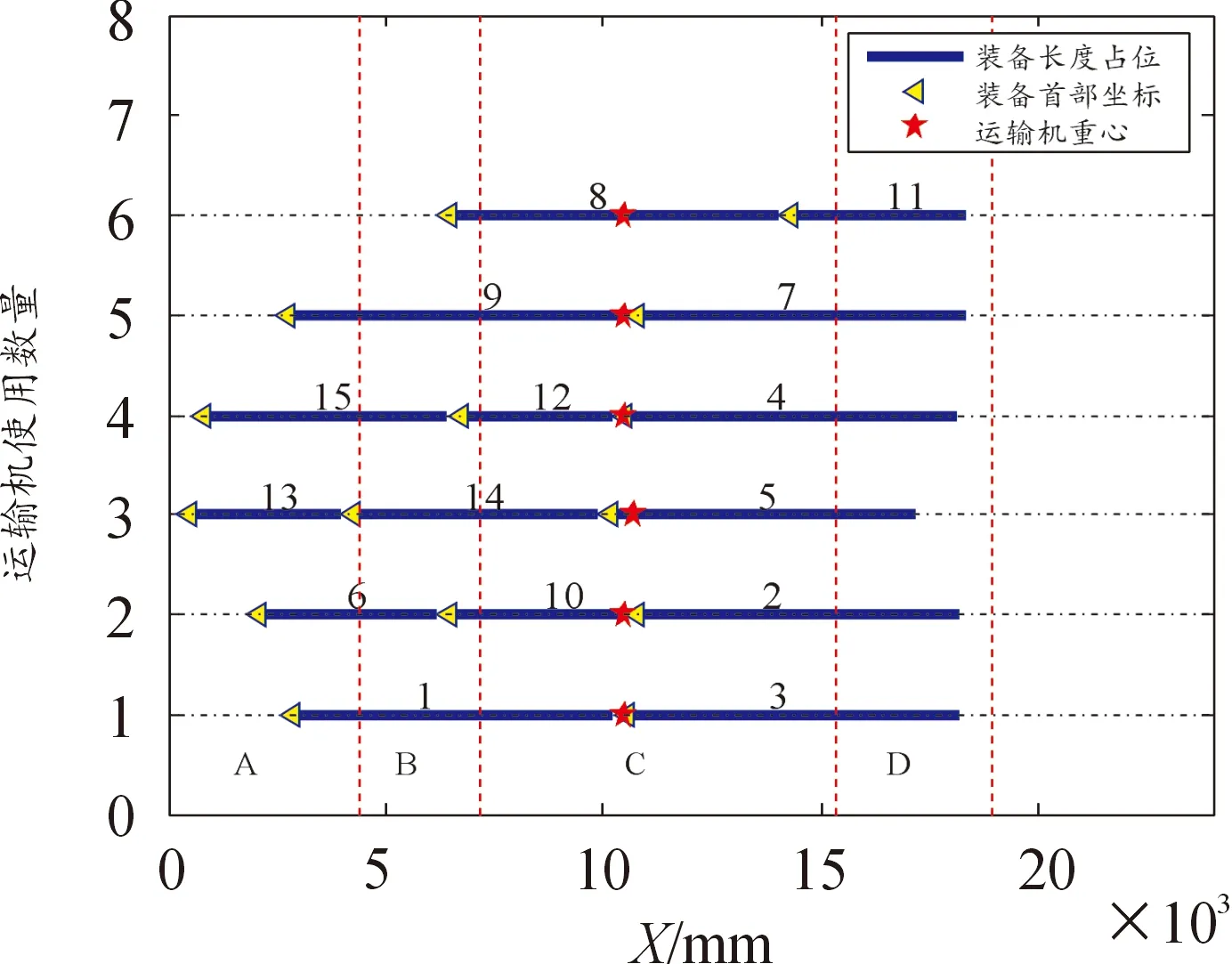
图4 待运装备的装载方案图

图4横坐标为运输机货舱中轴线X轴坐标,单位(1 000 mm),纵坐标为运输机使用数量。竖直虚线代表运输机货舱分区界线,横向点划线代表某一架次运输机货舱。粗实线代表某一台装备,线上编号代表装备编号,“△”代表装备的首部坐标,“★”表示在本架次运输机上所装载装备组成的装备序列的重心坐标(相对于货舱前部)。如第1架运输机,装载了编号为1和3的装备,首坐标分别为2 829.2、10 519 mm,由编号为1和3的2台装备组成的紧密装备序列的重心坐标为10 500.0 mm。从图4中可以看出优化后装载方案,装备居运输机中部装载,符合一般装载规律,空间利用合理。各架次运输机装备子序列重心可移动范围如图5所示。

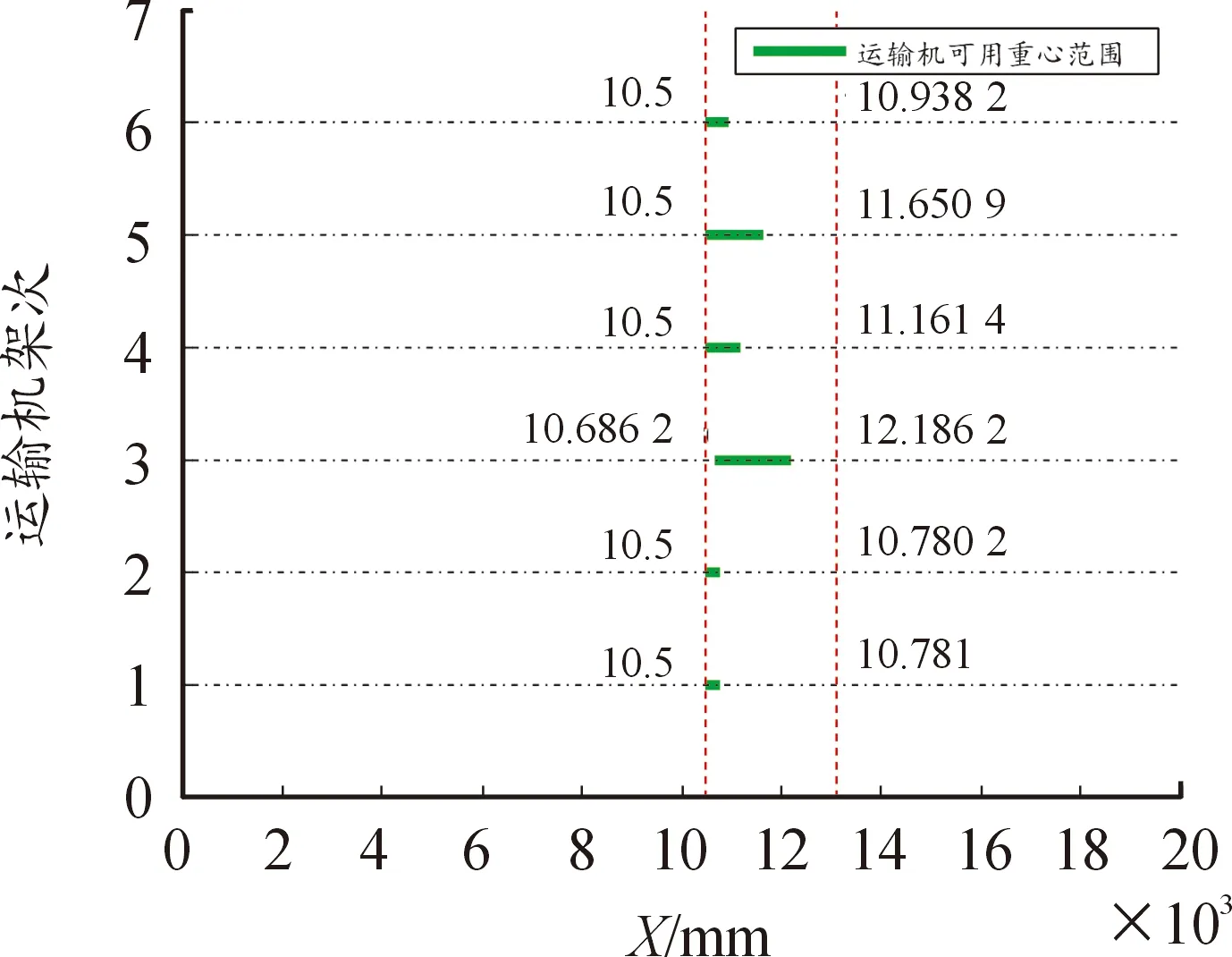
图5 各架次运输机装备子序列重心可移动范围

图5中运输机可用重心范围表示某架次运输机装载的装备序列重心还有一定的可调整范围。如第1架次运输机装载了编号为1和3的2台装备组成的装备序列,这个装备序列的重心可用范围为10 500～10 781 mm,实际上运输机X轴方向装载重心允许范围在10 500～13 500 mm。因此这3台装备组成的装备序列首坐标、装备间的最小间距均可在小范围内调整,只要重心仍在可用范围10 500～10 781 mm内即可。

图6为各运输机分区载重利用率。图7为各运输机空间与总载重量利用率,运输机总体空间与载重利用率较高。运输机的空间平均利用率83.8%,而运输机的载重平均利用率66.8%。因此,大型装备的长度是制约装载方案优化的主要因素。

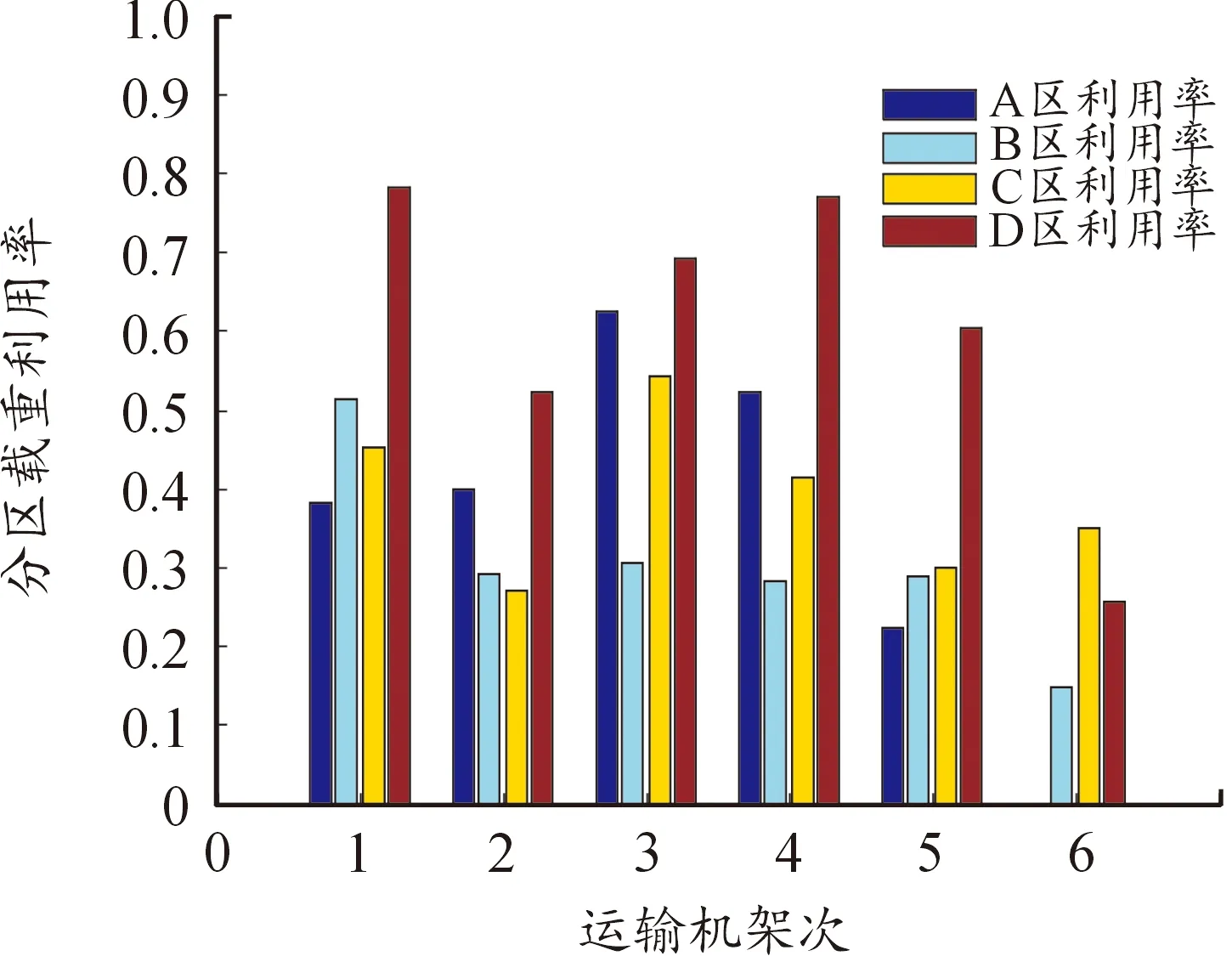
图6 各架次运输机分区载重利用率

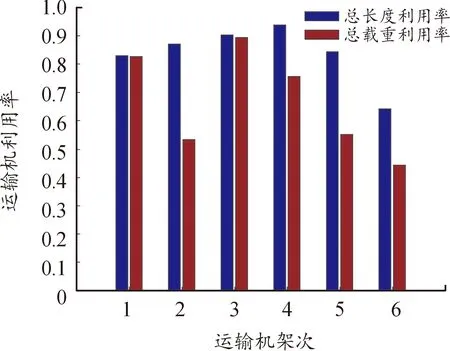
图7 各架次运输机空间与载重利用率

多台大型装备跨分区装载优化问题的算法,不仅可以适用于只使用某一个相同型号运输机多架次装载,通过输入不同型号运输机的参数,也同样适用于采用不同型号运输机装载优化问题,实现不同型号运输机同时混编运输的装载方案规划。

4 结论

1) 考虑了运输机的货舱总载重量、分区载重量限制、总长度限制条件,以最少架次运输机完成航空装载为目标,首先运用随机搜索算法获得初始解,然后利用禁忌搜索算法求解大型装备航空运输装载问题,可生成针对投送任务的装备装载优化方案,有助于实际装载方案拟制。

2) 采用运输机货舱总长度与总载重量约束作为分割装备序列的依据,符合大型装备普遍较长、线重比(重量与长度的比值)较大的特点。计算结果同样表明,长度是制约大型装备装载的主要因素。

3) 为了便于计算,将大型装备视为质量均匀分布的长方体,后续研究可考虑装备底盘型式、载重分布的实际情况,按照轮式、履带式装备分别校核运输机货舱分区载荷要求,使模型更加贴合装备实际特征。

4) 为了使装备重心范围严格约束,采用了运输机满载时的重心可用范围,然而在实际装载中如果运输机未满载,重心可用范围较满载时更宽,因此,下一步研究中,可结合运输机载重,限制重心可用范围。