基于发射药序列装填的火炮内弹道性能优化

李彦君,李全俊,韩智鹏,郭进勇,杨治林

(中国兵器装备集团 自动化研究所有限公司, 四川 绵阳 621000)

0 引言

模块装药目前广泛应用于大口径火炮,具有模块化结构特征,便于根据发射要求调节模块数量,为自动化装填和提高射速创造条件。然而目前模块装药在实际生产过程中均采用自由装填模式,可燃药盒内存在较大未利用空间,导致装填密度不高,极大地限制了火炮性能的提升,而目前通过发射药配方提升火炮性能已达到瓶颈,因此研究模块装药装填方式对火炮性能的影响具有重要意义。

近年来关于模块装药内弹道性能、热安全分析等方面的内容,国内外已有大量的研究。文献[1-2]中主要研究了模块装药的烤燃特性,建立了膛内模块装药二维非稳态烤燃模型,对烤燃过程进行了数值模拟,分析模块装药在火炮连发射击装填留膛的热安全性。文献[3-4]中研究了在外界不同热工况下,建立模块装药的二维非稳态烤燃模型,分析了模块装药的烤燃特性。文献[5-6]中设计模块装药可视化点传火模拟实验装置,分别针对单模块、双模块装药的点传火过程进行试验,建立了模块装药药盒破裂及药粒飞散三维非稳态气固两相流模型,分析了模块不同初始装填位置对模块装药点传火过程中药粒散布特性的影响。文献[7-9]中基于两相流内弹道燃烧理论模型,对模块装药进行膛内发射模拟,揭示了不同场景下弹道性能、模块着火燃烧现象、压力波动等情况。文献[10]为描述大粒子高密度装药的运动特性以及燃烧室内流场和火焰蔓延的发展过程,基于欧拉-拉格朗日方法,建立了一种新的改进简化的粒子元模型,研究了不同点火和装药条件对火焰传播性能的影响。文献[11]中根据模块装药的特点对现有模型进行改进和细化,使其更接近模块装药的内弹道实际过程。文献[12]中通过分析和计算建立了基于全膛烧蚀的内弹道模型,并导出求解算法。文献[13-15]中通过神经网络、切比雪夫建立动力学替代模型,分别使用博弈论和进化算法对内弹道计算的参数和弹道性能进行了优化。

综上所述,现有的国内外模块装药各类研究大都基于自由装填方式下进行,目前通过研究发射药配方的方式提升火炮初速性能已很难超过15%,忽视了模块装药装填方式本身对火炮性能的影响,本文针对序列装填模式下的模块装药技术展开研究。序列装填主要指发射药在可燃药盒的装填方式,目的在于通过某种装填策略提升有限空间里发射药装填密度,从而提升火炮发射性能。本研究中巧妙地将模块装药的序列装填方式转化为不等圆Packing问题(UCPP)[16-19],对比了序列装填与自由装填模式下火炮内弹道性能,验证了本研究中提出的序列装填方式的优越性,并通过改进的进化算法优化发射药序列装填布局方式,进一步提升火炮的内弹道性能。

1 基于模块装药序列混合装填的内弹道建模

1.1 发射药序列混合装填方式建模

目前传统的模块装药采用自由装填方式,如图1所示。自由装填主要存在的问题是装填方式随意,装药质量一致性差;可燃药盒装填空间未被充分利用,装填密度不高,发射性能尚有提升空间。

图1 模块装药自由装填方式

为解决上述问题,本文从序列装填方式出发,针对传统装填方式不足,采用新型分层装填模式,充分利用可燃药盒有限空间,装填方式如图2所示。从图2可以看出分层装填模式下,填充方式由若干层发射药粒堆叠而成,因此只需解决某一层的最大化装药问题就解决了整个装药方式问题(每一层装填方式相同)。

图2 模块装药序列装填方式

由于可燃药筒、发射药颗粒大小尺寸固定(排除生产误差),因此在可燃药筒(圆柱形)高度和发射药颗粒(圆柱形)高度确定的情况下(不同颗粒大小的发射药高度相同),发射药的序列装填方式问题可以转化为不等圆Packing问题(UCPP)。

对于本文的不等圆Packing问题,相应的问题描述如下:给定N个半径分别为Ri(i=1,2,…,N)的小圆,将这些小圆互不重叠、尽可能多地放入大的圆环里。如果将大的圆环形容器的圆心坐标固定为原点,外环半径为R,内环半径为r,将第i个小圆的圆心坐标记为(xi,yi),则不等圆Packing问题转换为寻找布局X=[(x1,y1,R1),(x2,y2,R2),…,(xN,yN,RN)],以满足以下目标函数

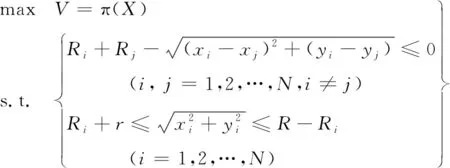
(1)

式中:V=π(X)表示序列装填方式X与弹丸初速V之间的映射关系;s.t.表示发射药截面圆在可燃药筒截面圆环内,且发射药截面圆之间互不相交的约束条件。

1.2 模块装药内弹道模型

本文采用基于多孔火药的经典内弹道模型,其模型方程组为:

几何燃烧定律

(2)

式中:Z为火药已燃相对厚度;ψ为火药已燃百分数;χ、χs、λ、λs、μ为火药形状特征量。

燃速定律

(3)

式中:e1为药粒弧厚;u1为燃速系数;p为火炮膛压;n为燃速指数。

弹丸运动方程

Spdt=φmdv

(4)

内弹道基本方程

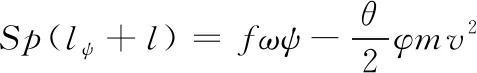
(5)

式(3)、式(4)中一些参数的计算方式为:

(6)

由于考虑发射药装填过程中至少存在2种以上不同半径的发射药,假设某一层中第i个装填的发射药长度为hi,发射药密度为δi。根据1.1节中序列装填的建模内容,得出式(5)中装药质量ω可以表示为

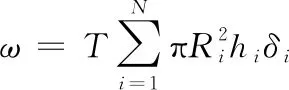
(7)

式中:T为发射药装填层数,表示一个可燃药盒装有T层发射药堆叠而成;N为一层发射药装填的总个数。

内弹道方程的求解目前主要采用计算精度高、运算速度快的四阶龙格-库塔法[11-12],求解方法如下:

根据一阶微分方程组

(8)

式中:gj为k的第j个因变量;gj0为z=z0时的初值。

式(8)方程的解为

(9)

式中:步长h=ki+1-ki;i为自变量离散点个数;

2 基于改进遗传算法的序列混合装填内弹道性能优化

本文针对目前模块装药自由装填方式下,发射装药密度低,发射性能未充分释放的问题,采用不同颗粒大小的发射药序列装填分层混合装填模式进行装药,并通过进化算法求解序列装填的最佳布局方式,实现内弹道性能的优化。布局方式指不同发射药粒在可燃药盒里的排列方式。

由前文1.1节序列装填建模内容可知,布局方式问题可以转化为圆环内不等圆的Packing问题,Packing问题主要研究如何在有限的空间内最大化放置物品时的容器利用率,容器利用率越高,可燃药盒装填发射药的质量就越多。Packing问题是具有NP难度的组合优化问题,目前求解这类问题多数采用启发式算法[16-19]。

2.1 一种改进的遗传算法

遗传算法具有很强的全局搜索能力,但也存在容易陷入早熟、依赖初始种群、局部搜索能力薄弱的缺陷,针对以上问题和本文研究内容,提出一种改进的遗传算法。

1) 染色体编码

本文采用实数编码,故由基因变量构成的染色体个体可以表示为

Xu=[(x1,y1,R1);(x2,y2,R2);…;(xN,yN,RN)]

(10)

式中:x表示发射药颗粒截面圆圆心横坐标;y表示发射药颗粒截面圆圆心纵坐标;R表示发射药颗粒截面圆半径;N表示可燃药盒装填的第N个发射药,由于装填过程发射药颗粒大小随机选择,导致不同装填布局方式下可燃容器里发射药个数不同,但尽可能保证可燃容器装满,充分利用容器空间;Xu为种群中第u个染色体,表示可燃药盒装填的发射药坐标和颗粒大小信息集合。

2) 适应度函数及约束条件

由于本文目标在于优化枪炮的内弹道性能,涉及膛压和弹丸初速,则适应度函数设计为

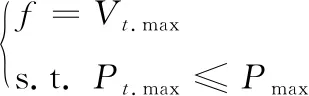
(11)

式中:Vt.max表示内弹道v-t曲线速度的最大值;s.t.表示约束条件;Pt.max表示内弹道p-t曲线膛压的最大值;Pmax表示膛压的极限值,本文中取580 MPa。

3) 选择算子

初始种群采用随机地方式产生,并满足式(1)中的约束条件s.t.,初始种群可以表示为

H=[X1,X2,…,Xgn]

(12)

式中:gn表示种群染色体个数;H表示初始种群集合。

本研究中用轮盘赌方式选择父代,并采取最优保留策略,轮盘赌概率计算可以表示为

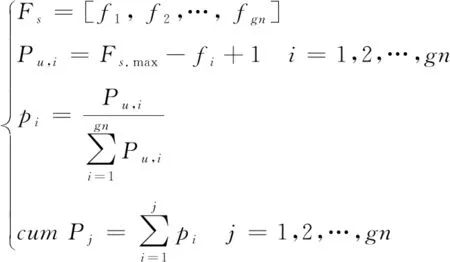
(13)

式中:Fs表示种群适应度值集合;Fs.max为种群适应度值集合中最大值;fi表示第i个染色体适应度值;Pi为选择第i个父代时轮盘赌被选中的概率;cumPj表示前j个染色体被选中为父代的概率值。

父代选择过程可表示为

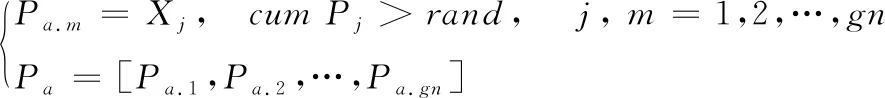
(14)

式中:Pa.m表示被选中的第m个父代染色体;rand为0～1的随机数;Pa为选中的父代染色体集合。

4) 交叉算子

交叉过程中,交叉概率越大产生的新子代个体就越多,但同时种群中优秀个体被替换掉的概率就越大;交叉概率过小,产生新子代的个体就越少,导致搜索进程过于缓慢。因此,本文采用一种自适应的交叉策略,在避免优秀个体被替换和搜索进程较慢之间动态平衡。

(15)

式中:f、fmean、fmax分别表示迭代过程中交叉操作前个体适应度值、种群平均适应度值、种群最大适应度值;pe1、pe2为2种不同的交叉概率,其中pe1>pe2,本文pe1取0.9,pe2取0.4。

交叉操作步骤:

a) 选出2个父代染色体,分别进行染色体分裂,分裂过程如图3所示,染色体沿虚线分成2个相同的半圆环,半圆环内部的小圆保留,与虚线相交于两点的小圆将会被剔除,形成2条半圆环形染色体。

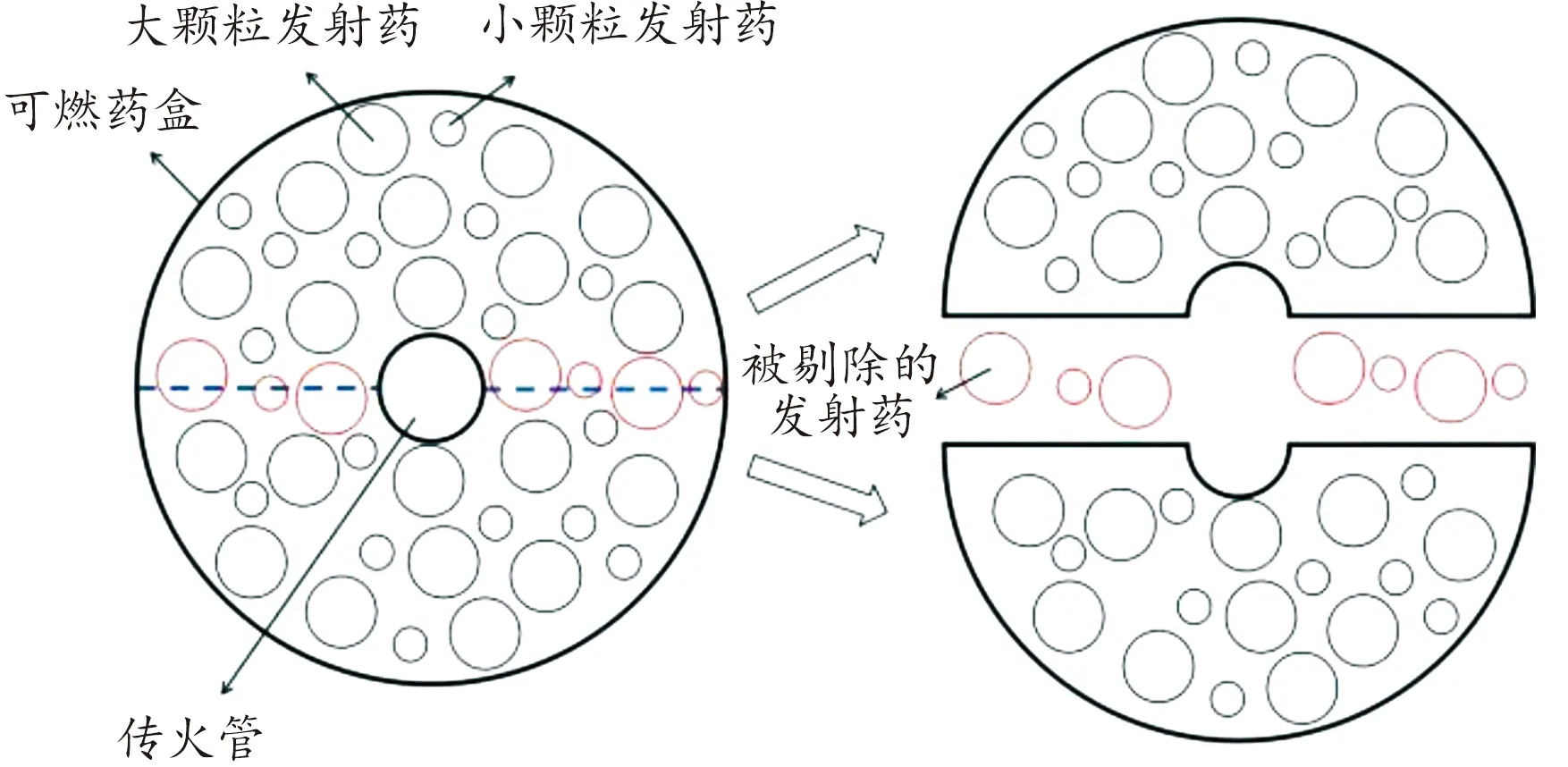
图3 父代染色体分裂方式

b) 将2个父代的2条半圆环形染色体,两两结合,形成新的2个子代染色体,2个子代染色体由于a)步骤剔除部分装填的小圆存在一定未利用空间。因此,在空间里随机补充2种不同大小的小圆,直到圆环装满不能装更多为止,结合过程如图4所示。

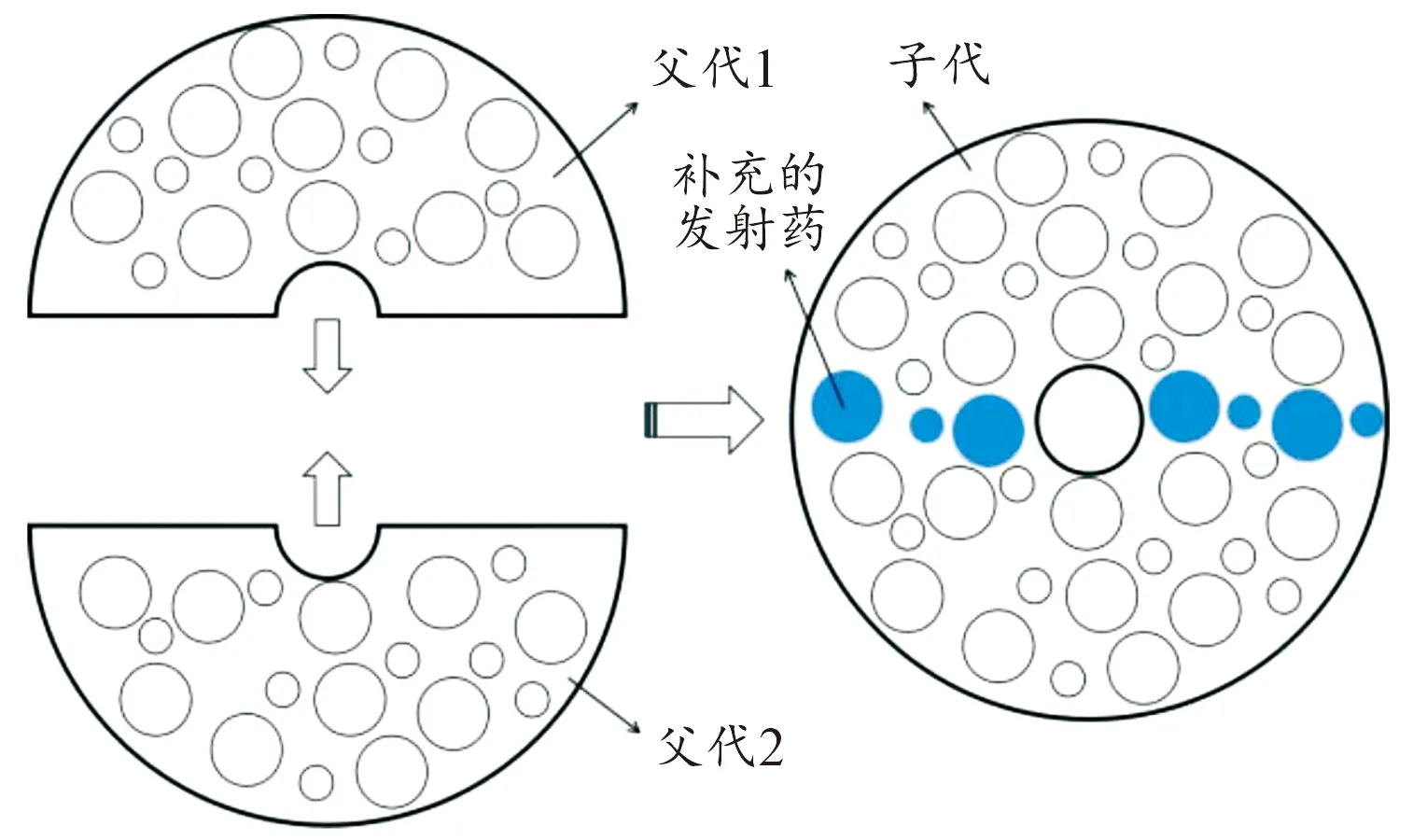
图4 子代染色体结合方式

5) 变异算子

同理,变异概率过小,容易陷入近亲繁殖,不易产生出新的优秀个体;变异概率过大,则退化为随机搜索。因此,变异操作概率也采用自适应调整策略。

(16)

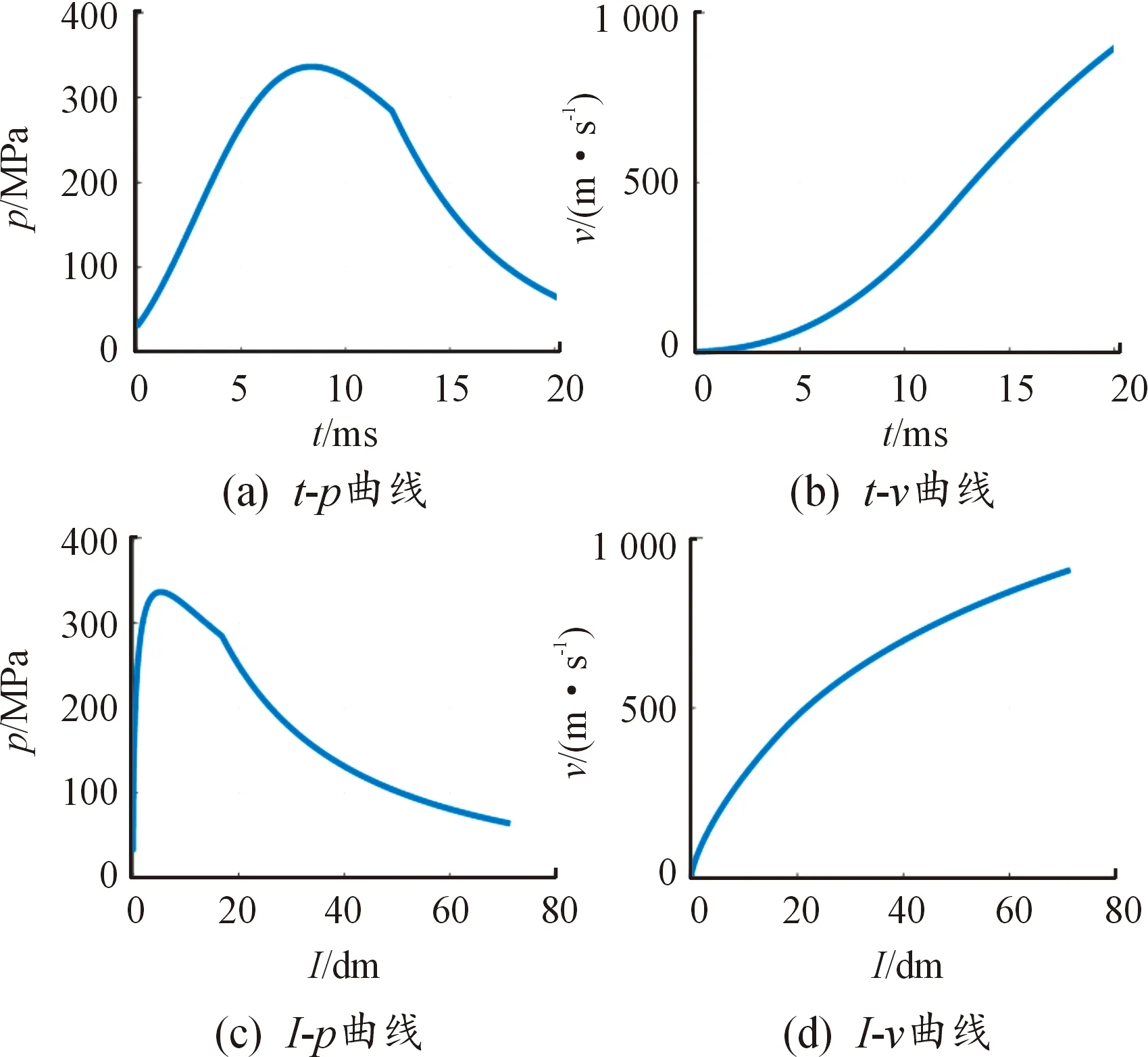
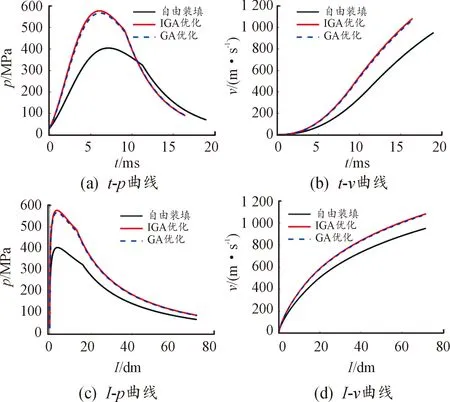
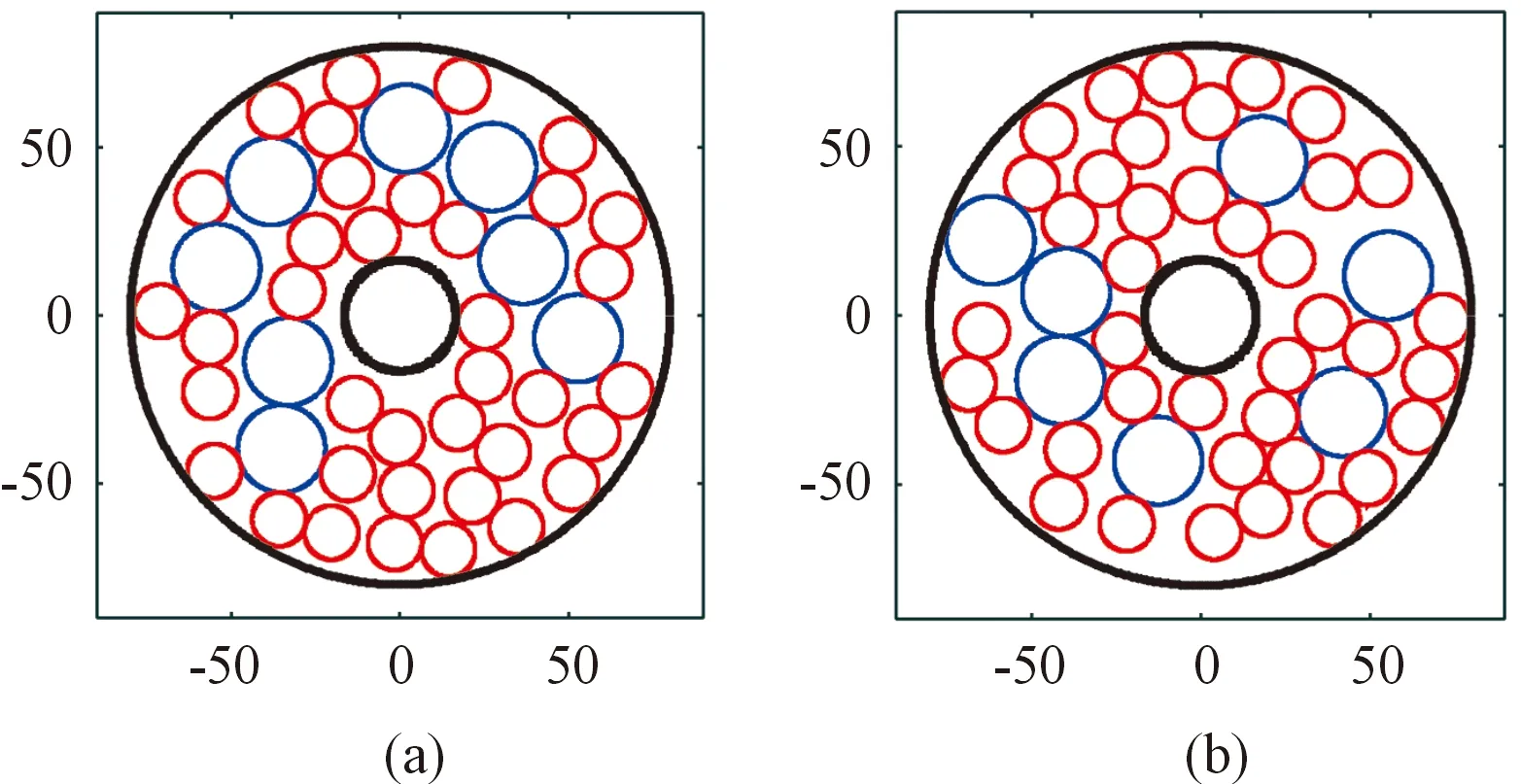
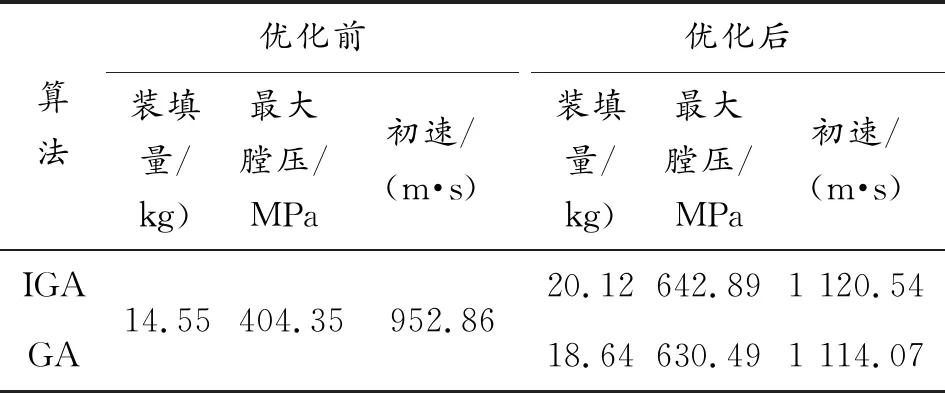
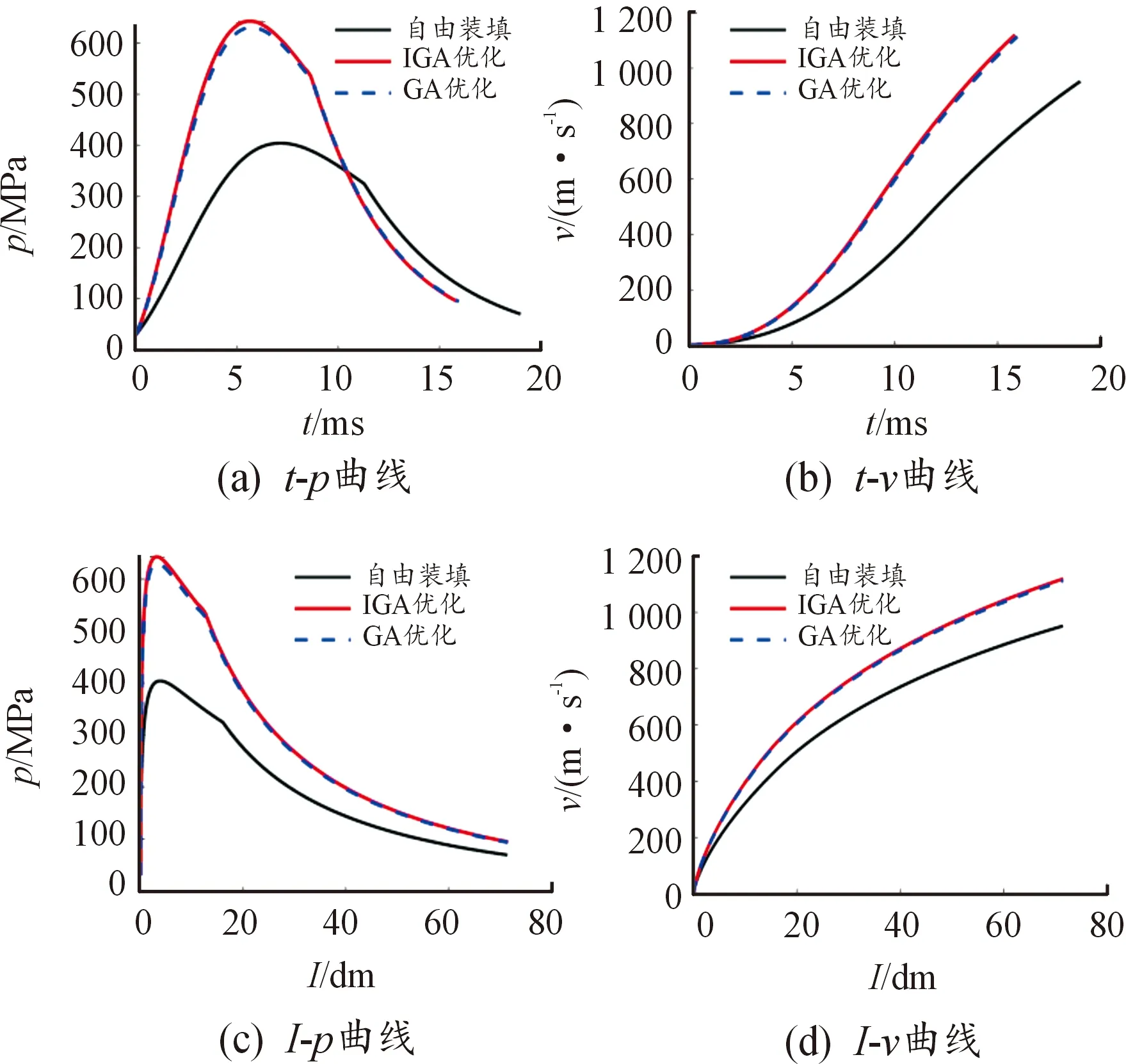
式中:fmin.o表示迭代过程中交叉操作后子代种群最小适应度值;fmean.o表示迭代过程中交叉操作后子代种群平均适应度值;fmax.o表示迭代过程中交叉操作后子代种群最大适应度值;pm1、pm2为2种不同的变异概率,其中pm1

变异操作步骤:

a) 随机剔除交叉后圆环内若干个小圆,剔除个数控制在小圆总数的50%以内。

b) 由于a)步骤剔除小圆导致圆环空间未被填满,重新随机补充2种不同大小的小圆,直到圆环装满不能再装填为止。

2.2 基于改进遗传算法内弹道性能优化的布局方式求解

根据前文介绍的序列装填方式模型、模块装药内弹道模型嵌入改进的遗传算法,对序列装填方式下内弹道性能进行优化求解,具体求解流程如图5所示。

图5 序列装填布局方式求解流程

求解流程描述:

1) 根据发射药序列装填模型,依次随机在圆环(可燃药盒)内放置不同半径小圆(不同颗粒发射药),放置时需满足式(1)中约束条件s.t.,尽可能多地放置小圆,直到圆环内不能放置更多小圆为止,形成一个染色体X。

2) 重复步骤1)gn次,形成包含gn个染色体的初始种群H。

3) 根据式(13)轮盘赌策略筛选出种群H的父代Pa。

4) 根据种群父代染色体Pa参数信息,结合式(7)计算发射药装填质量。

5) 根据内弹道方程组及求解式(2)—式(6)、式(8)、式(9),求解出内弹道p-t曲线、v-t曲线,找到父代最大膛压Pt.max和最大初速Vt.max。

6) 根据式(11)进行父代适应度值计算,并找出父代最佳个体。

7) 根据交叉算子相关方式对父代进行交叉操作。

8) 根据变异算子相关方式对父代进行变异操作。

9) 经过交叉、变异操作后形成子代,套用步骤4)、步骤5)内弹道方程组及求解式(2)—式(9),找到子代最大膛压Pt.max和最大初速Vt.max。

10) 根据式(11)进行子代适应度值计算,找出子代最佳个体和最差个体,并将子代最佳个体作为该轮迭代的最优个体。

11) 将父代最佳个体替换子代最差个体。

12) 判断是否满足停止条件,为否,则进入下一轮迭代的父代选择,重复步骤3)—步骤11),迭代更新子代最优个体;为是,则输出该轮子代最优个体,作为全局最优解,并停止搜索。

3 算例

为验证发射药序列装填对内弹道性能的影响以及优化后内弹道性能的提升情况,本文以45倍口径155 mm火炮为算例进行数值模拟分析。

该口径火炮装填与结构原始参数如表1所示。

表1 45倍口径155 mm火炮装填与结构参数

根据表1参数进行数值仿真,输出内弹道性能数据表及曲线,如表2、图6所示。由表2数据可知,该口径火炮挤进压力为30 MPa,发射药点火8.37 ms左右膛压达到最大336.54 MPa,经过20.21 ms后,达到初速906.69 m/s。最大膛压与初速值与参考文献[20]中45倍口径155 mm火炮内弹道实测性能基本一致,相对误差均小于1%,表1的内弹道结构参数较为准确。

表2 155 mm火炮内弹道性能数据

图6 155 mm火炮内弹道性能曲线

本文采用发射药序列装填方式,充分考虑可燃容器尺寸约束,真实模拟装填过程,通过改进遗传算法求解最佳装填布局方式,从而优化内弹道性能。

根据中国兵器工业集团375厂(后文简称:375厂)发射药生产数据,可知可燃药盒的内径为160 mm,传火管外径为37 mm,可燃药盒高度173 mm,传火管与可燃药盒之间的区域为发射药粒装填空间,如图7所示。目前375厂所生产的可燃药盒由2种粒状发射药混合装填而成,发射药粒尺寸分别为:高度28 mm,直径26 mm以及高度18 mm,直径16 mm,发射药密度为1.6 g/cm3,自由装填方式下一个可燃药盒能装填2.3～2.55 kg发射药,且装药量的概率在装药量区间内满足N～(2.425,0.041 7)的正态分布。

图7 可燃药盒有关尺寸

为方便序列装填在工程上的实现,本文采用相同高度的发射药粒分层装填进行模拟,尺寸为:高度28 mm,直径分别为26 mm和16 mm,保证每一层的发射药装填平整,一个可燃药盒可以铺设6层发射药,由于发射药长径比分别为:1.08、1.75,两者相差不大,故忽略不同粒径对发射药燃烧性能、药粒强度等差异的影响。

根据上述尺寸数据和式(1)转换成不等圆装填约束条件,结合内弹道模型、前文结构参数与改进的遗传算法,对适应度函数进行优化,求解出相应的最佳序列装填方式。在优化求解过程中,不同的序列装填方式对应不同的发射药装填量,也就对应不同的内弹道性能、不同的适应度函数值,优化结果如表3、图8、图9所示。

表3 膛压约束下的优化结果对比

图8 膛压约束优化前、后内弹道性能对比

图9 膛压约束序列装填布局方式优化对比

其中优化前,每个可燃药盒装填量按375厂自由装填模式下的装填量均值2.425 kg计算,采用6盒装药的装药量为14.55 kg,对应的初速为952.86 m/s。本文对比了标准遗传算法与改进遗传算法优化效果,标准算法优化后装填量为18.64 kg,初速为1078.62 m/s,改进算法优化后的装填量为18.85 kg,初速为1084.61 m/s。结合表3和图8可以看出,序列装填模式下的内弹道性能无论采用哪种方式优化,优化后的内弹道性能都比自由装填模式下更好,在最大膛压580 MPa的约束条件下,初速分别提升了13.20%、13.83%,装药量分别提升28.11%、29.55%,改进算法的优化效果比标准算法更好。图9展示了膛压约束下2种算法求解的某一层最佳序列装填布局方式对比,图9(a)、图9 (b)两图分别为IGA、GA算法求解的序列装填布局方式,红色和蓝色圆圈分别代表小颗粒和大颗粒发射药俯视面,黑色圆环内部表示有效装填区间,内环为传火管俯视面,外环为发射药盒俯视面。

本文还研究了无膛压约束下序列装填火炮的内弹道性能。表4可以看出在,无膛压约束下,可燃药盒序列装填量、膛压、初速进一步升高,标准算法优化后装药量为19.89 kg,最大膛压为630.49 MPa,初速为1 114.07 m/s;改进算法优化后装药量为20.12 kg,最大膛压为642.89 MPa,初速为1 120.54 m/s。相比于自由装填方式,装药量分别提升36.70%、38.28%,初速分别提升了16.92%、17.60%;与膛压约束优化相比,装药量分别提升了6.71%、6.74%,膛压分别上升了8.71%、10.84%,初速却分别只提升3.29%、3.31%。图10展示了无膛压约束优化下,序列装填与自由装填内弹道性能的对比;图11为图10优化内弹道性能后对应序列装填布局方式的解,图11 (a)、图11 (b)两图分别为无膛压约束下IGA、GA算法求解的序列装填布局方式。

表4 无膛压约束的优化结果对比

图10 无膛压约束优化前、后内弹道性能对比

4 结论

针对目前模块装药自由装填模式下可燃药筒内存在较大未利用空间,装填密度不高,内弹道性能未充分得到释放的问题,采用一种新的装填模式-序列装填来提升优化火炮内弹道性能。序列装填考虑了可燃药盒的尺寸约束,巧妙地将发射药装填问题与不等圆装填问题结合,并用改进的优化算法对内弹道性能进行优化求解。结合算例分析,得出以下结论:

1) 模块装药采用序列装填模式装药量有显著提升,以国内目前155 mm火炮广泛采用的可燃药盒为例,在无膛压约束下装药量相比自由装填方式提升超过35%,火炮初速提升超过16%,而目前通过配方研究提升初速已很难超过15%。

2) 序列装填确定了药粒的大小与装填位置,不像自由装填那样装药量存在较大的波动,确保了火炮内弹道性能的可靠性与稳定性。

3) 随着发射药装填量的增加,火炮膛压的增幅明显快于初速增幅。

4) 相比于标准GA算法改进后的遗传算法在全局优化方面的效果得以提升。