舰载机无杆式牵引车行驶稳定性分析

2023-09-03戚基艳许浩洋

兵器装备工程学报 2023年8期

戚基艳,许浩洋,苏明

(1.沈阳理工大学汽车与交通学院, 沈阳 110159;2.辽宁省安全科学研究院, 沈阳 110004)

0 引言

航空母舰是海上作战的重要机动平台,象征着一个国家的综合国力。舰载机是航母的核心攻防力量,随着航母工程的发展,舰载机性能的不断提升,如何提高其出动强度[1]受到越来越多人的关注[2-5]。舰载机无论是起飞前、降落后的移动还是进出机库,都需要依靠牵引车的顶推或者牵引来完成,因此舰载机牵引车逐渐进入人们的视野[6-7]。舰载机牵引车分为有杆式和无杆式2种。随着智能制造业的快速发展,无杆式牵引车能够更好地应用智能制造技术,结构布置紧凑,牵引能力更强,机动性和灵活性更好,将逐步取代有杆式,成为舰载机牵引车发展的趋势[8-9]。牵引车是舰载航空领域装备数量最大、使用频率最高的保障车辆[9],其行驶的稳定性直接影响舰载机的出动效率和调运安全。舰基作业面狭窄,作业环境复杂,牵引的舰载机体积和质量庞大,加之航母航空甲板复杂不规则的运动影响,因此,舰面行驶的牵引车行驶特性比岸基牵引车更复杂[10]。牵引系统行驶不稳定问题的加剧,直接影响舰载机的调运安全,甚至造成甲板事故,从而影响舰船整体的战斗力发挥。

受海浪、海风等海洋环境的影响,舰船在海上航行时会产生多个自由度的复杂不规则运动。舰船作为研究舰载机牵引车的运动参考系,是非惯性参考系[10]。舰船运动给舰载机牵引车的运动施加了多方向的惯性力矩和惯性力,增加了其运动状态的复杂性,导致行驶不稳定因素增加。目前国内外对于牵引车运动的研究,多数是以岸基作业环境为背景[11-12],建立的运动学和动力学模型及其相关分析不需要考虑舰船运动的影响,不能应用于描述舰面行驶的牵引车运动特性。舰载背景相关的牵引车运动学研究大多也没有考虑舰船的运动影响[13-15]。文献[16]建立了运动甲板上牵引车—舰载机系统动力学模型,仿真分析了牵引车的重要使用因素对牵引车和舰载机行驶状况的影响,为本文的研究提供了思路,但是没有对行驶特性进行深入的理论研究。本文考虑舰船运动的影响,建立舰载机无杆式牵引车的动力学数学模型,深入研究其在舰船甲板面上的操纵特性,为提高其行驶稳定性提供理论支持,从而为提高航母机动性和战斗力提供可靠的保障。

1 舰载机无杆式牵引车系统动力学模型

1.1 舰船运动模型

图1 舰载机无杆式牵引车系统模型

假设船体为刚体,相对于质心运动。船体的姿态可以通过从惯性坐标系做2次旋转来实现[17]。旋转方案由于旋转轴和旋转次数不同可以有多个选择[18],为了后续研究的准确性,本文选择转角物理意义明确且在比较简单情形下即可描述其性质的方案,该方案也是获得广泛应用的旋转变换关系[19]。

在On-xnynzn中船舶的运动可用矢量表示为

(1)

式(1)中:xn,yn,zn是矢量Rn的3个分量,代表船舶的3个空间位置;φ、θ、ψ代表舰船的3个姿态角:横倾角、纵倾角、方位角。同样,在Oj-xjyjzj中,舰船的6自由度运动可以描述为:跟随舰船3个附体坐标轴的移动以及绕3个附体坐标轴的转动,用矢量表示为

(2)

式(2)中:uj、vj、wj是船舶的重心在附体坐标系的速度分量,分别是纵荡速度、横荡速度和垂荡速度;pj、qj、rj为xj、yj、zj轴的瞬时角速度,分别是横摇角速度、纵摇角速度、以及艏摇角速度。

综合以上分析,舰船的相对运动学方程可以表示为

(3)

(4)

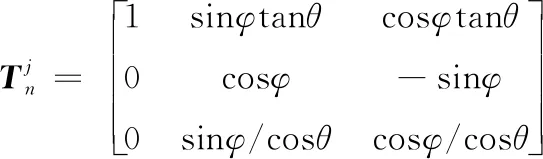
(5)

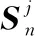
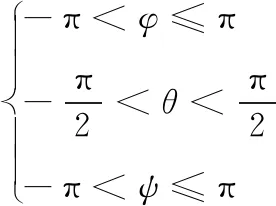
(6)

舰船在航行时,在海浪作用下或者其他特定情况下,可认为舰船运动是带有一定周期性的运动,其中纵摇、横摇和垂荡3种运动的幅度较大,对舰船上设备的影响最明显[21],是本文研究的舰载机牵引车系统运动主要考虑的因素。从工程应用的角度,认为舰船不同状态的运动是彼此不耦合的[2],通常采用简化模型来表示船体的纵摇、横摇和垂荡运动规律。在On-xnynzn中,舰船的运动规律可以表示为

(7)

式(7)中:φ0、θ0、z0为船体运动的幅值;ωφ、ωθ、ωz为船体运动的遭遇频率;ηφ、ηθ、ηz为船体运动的初始相位角。

根据以上分析,舰船的速度、加速度、角速度和角加速度在舰船坐标系Oj-xjyjzj中的表达式为:

(8)

1.2 系统运动学模型

牵引车(舰载机)在惯性坐标系On-xnynzn中的绝对运动描述为:牵引车连体坐标系Oi-xiyizi(i=1,2)在舰船坐标系Oj-xjyjzj中的相对运动和舰船坐标系Oj-xjyjzj自身的牵连运动之和。

牵引车(舰载机)在惯性坐标系On-xnynzn中的绝对速度和加速度为:

(9)

牵引车和舰载机的转动角速度和角加速度可以表示为

(10)

(11)

1.3 系统动力学模型

舰载机无杆式牵引车在舰面行驶速度较低[9],侧向力可以通过线性轮胎模型表示为

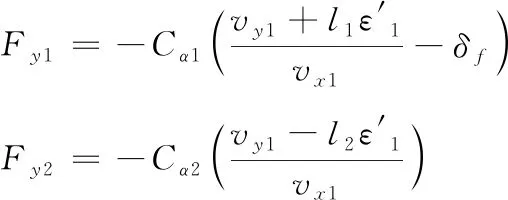
(12)

式(12)中:Cα1、Cα2为正,这里指整个车轴的侧偏刚度;vx1、vy1是牵引车在坐标系O1-x1y1z1内沿坐标轴的行驶速度。根据式(11)可知:

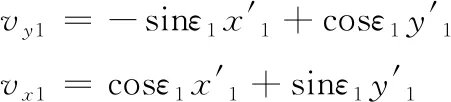
(13)

综合以上分析,以∑Fxi、 ∑Fyi(i=1,2)分别表示牵引车(舰载机)在Oi-xiyizi坐标系内沿横坐标轴xi和纵坐标轴yi方向的合力,以∑Mzi表示绕zi轴的合外力矩,借鉴汽车基本操纵模型假设,牵引车(舰载机)的运动方程可以表达为

(14)

式(14)中:mi(i=1,2)是牵引车(舰载机)的等效质量[8];Izi是牵引车(舰载机)的转动惯量。假设牵引车牵引舰载机匀速行驶于舰船甲板面,此时∑Fxi=0,式(14)简化并展开得

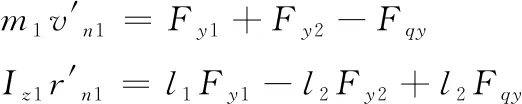
(15)

2 系统横向稳定性分析

2.1 系统稳定性判断

AX″(t)+BX′(t)+HX(t)=F(t)

(16)

其中:

根据式(16)可知如下关系成立:A=AT,B=BT,H=HT,A、B、H均是对称矩阵,只有当牵引车处于纯滚动的理想状态时,其稳定裕度才为零,即l1Cα1=l2Cα2时,式(16)中的2个自变量才是非耦合,除此之外,其他情况2个自变量均耦合。下面从这2种情况分别分析牵引车系统的稳定性。

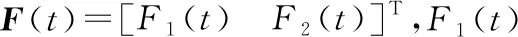
其次分析一般状态,即l1Cα1≠l2Cα2时,式(16)可以看作是2自由度自激振动系统,为了能够研究系统的稳定性,假定系统解的形式为:

xζ(t)=Cζestζ=1,2

(17)

式(17)中:s为待定的复数;Cζ为xζ(t)的幅值。s的实部决定了系统的阻尼,虚部表示系统的固有频率,将解代入系统的自由振动方程中(令F(t) =0),可得:

([A]s2+[B]s+H)Cest=0

(18)

为求Cζ的非零解,令Cζ的系数行列式等于0,则可推出式(18)特征方程为:

D(s)=|[A]s2+[B]s+H|=0

(19)

式(19)展开得到一个关于s的4阶多项式方程,其形式为:

D(s)=a0s4+a1s3+a2s2+a3s+a4=0

(20)

用代数稳定判据-劳斯判据对高阶系统的稳定性进行判断,通过对特征方程列出劳斯表可得式(20)所涉及的4阶系统稳定的充分必要条件为:

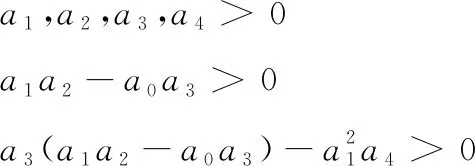
(21)

结合特征方程(20)和特征多项式(21)以及运动方程(16)可知:由于a4=0恒成立,因此系统一定不稳定。综合以上2种情况分析可知,舰船上,无杆式牵引车牵引舰载机在舰船甲板面匀速行驶时,系统一定是不稳定的。

进一步分析不稳定的表现形式。设λ1,2=m±jn为系统的一对共轭特征根,则系统的阻尼比可表达为[23]:

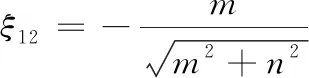
(22)

系统稳定的充分必要条件是根应该有非正实部,但是因为系统不稳定,可知式(22)中m>0恒成立,当n=0时,阻尼比ξ=-1,舰载机无杆式牵引车系统将发生“折叠”现象,即状态是按指数变化规律的单调分歧失稳;当n≠0时,阻尼比-1<ξ<0,将发生“横向摆振”现象,即幅值渐增的动态振荡失稳。因此,可以通过计算舰载机无杆式牵引车系统的阻尼比判断系统的失稳形式。

2.2 系统的稳态响应

在汽车系统动力学中,稳态响应特性代表了车辆的基本操纵性能,用来衡量输入为定值时系统的响应。借鉴这个思路,对目标舰载机无杆式牵引车进行稳态响应分析。由于考虑了舰船运动的影响,所建立的系统方程是一个二阶方程,系统的输入项F(t)不仅包括了转向盘角输入参数δf,还包括了与牵引车运动和舰船运动等有关的参数,因此不能借鉴单一输入为转向角的汽车系统动力学分析的思路,拟从受迫振动的角度分析牵引车的稳态响应。把外部激励F(t)简化为

Fζ(t)=Fζosinωt,ζ=1,2

(23)

式(23)中:ω为外部激励的频率;Fζo为简谐力对应的静态力。则可知对应的微分方程的稳态解为:

xζ(t)=Xζsinωt,ζ=1,2

(24)

将式(23)和式(24)代入式(16)可得:

(25)

根据克莱姆法则,可求得式(25)的稳态运动振幅为:

(26)

把式(26)代入式(24)可以得到系统稳态解的完整形式。根据式(26)可知,舰载机无杆式牵引车的稳态运动振幅与舰船运动参数息息相关,因此在研究其相关运动学问题时,不能忽略舰船运动的影响,否则大大降低研究结果的可信度。其次,从机械振动学角度考虑,为了保持系统的稳定状态,不仅要减小系统的固有振幅,还要防止系统自身2种运动(侧向运动和横摆运动)叠加发生共振。为了减小振幅,假设X1(ω)=0,得到此时激励力之间的关系为:

(27)

将式(27)代入X2(ω)=0中,可得关系式为:

或

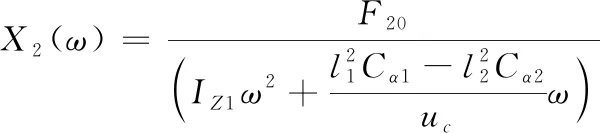
(28)

在外激励频率不为0的情况下,激励力始终存在,振幅始终不为0,因此2个变量相对应的振幅不能同时为0,目标牵引系统不能被精确的控制在理想的共振频率为0的状态。

2.3 系统频率响应分析

在正弦输入信号作用下,系统输出的稳态分量称为频率响应,频率响应与正弦输入信号之间的关系称为频率特性[24]。频率响应函数为系统提供了对各种不同频率成分响应的完整描述,最后的输出实际上就是这些响应的线性叠加,因此将外部激励简化为简谐力,输出相当于响应的一种分量,具有一定的可参考性。频率响应函数间接的为牵引系统对任何形式的输入响应提供了一个完整的描述。下面继续讨论如何对考虑舰船运动的舰载机无杆式牵引车系统的频率响应进行分析。

假设系统输入为正弦波,外部激励F(t)表示为:

Fζ(t)=Fζoeiωt,ζ=1,2

(29)

式(29)中:ω为外部激励的频率;Fζo为对应的静态力。则可知对应的微分方程的稳态解为:

xζ(t)=Xζeiωt,ζ=1,2

(30)

一般情况下,式(30)中Xζ是复数,取决于激励频率ω和系统参数,代表了xζ(t)对输入响应的幅值和相位变化,且遵循x′=iωx的关系,将xζ(t)代入式(16),再约掉eiωt,重新整理得到:

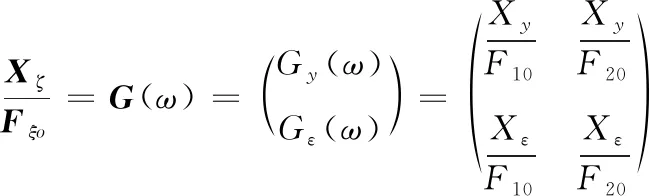
(31)

式(31)中:G为方程的“传递函数”,代表了系统输出与输入的关系。系统输出、输入的幅值比是频率的函数,即为幅频特性

G(ω)=KD(ω)

(32)

式(32)中:

根据式(31)和式(32)就可以分析不同的输出对不同的输入的响应。进一步对式(32)进行整理,式(31)每一项输出与输入的比值均可以表示成如下的形式,即

Lζξ(ω)+Qζξ(ω)i

(33)

式(33)中:ζ、ξ分别代表式(31)中的行和列。根据式(33)的整理,能够得出系统的幅频特性和相频特性分别为:

(34)

(35)

基于稳定性分析、稳态响应分析以及频率响应分析,能够完整地描述舰载机无杆式牵引车系统的操纵特性,从而为分析不同行驶工况下目标系统的行驶稳定性提供了理论支撑和判定依据。

3 质心位置对牵引车行驶稳定性的影响

质心位置是影响汽车横摆稳定性的重要指标[25]。根据式(16),通过建立舰载机无杆式牵引车动力学仿真模型,分析牵引车质心位置对稳定性的影响。牵引车质心位置包括质心高度和质心纵向位置,相关参数的取值不仅直接影响牵引车系统的行驶稳定性[17],同时也影响垂向载荷和侧偏刚度的变化,进一步影响了侧偏附着极限。拟采用单一控制变量法,以牵引车横摆角速度和侧向速度为参考变量,分析在不同海况下,随着质心位置的变化,参考变量的变化规律,通过敏感度分析,量化影响程度。为了实现舰载机出动强度的最大化,考虑舰载机在舰船甲板面能够成功开展战斗勤务活动和正常起降的极限范围,仿真实验的海况等级取5～7级[26],探讨在不同的海况下质心位置的变化对行驶稳定性的影响。相关牵引车的参数选取与文献[17]相同。

3.1 质心高度

牵引车质心高度h1分别从标准值0.3 m上移和下移0.2 m,即取值0.1、0.3、0.5 m。如图2和图3所示,分别代表4、5、6级海况下,牵引车系统的侧向速度和横摆角速度的整体变化及其局部放大图(图2、图3中括号前面数值代表海况等级、括号内的数值代表质心高度的取值)。

图2 质心高度变化的侧向速度对比

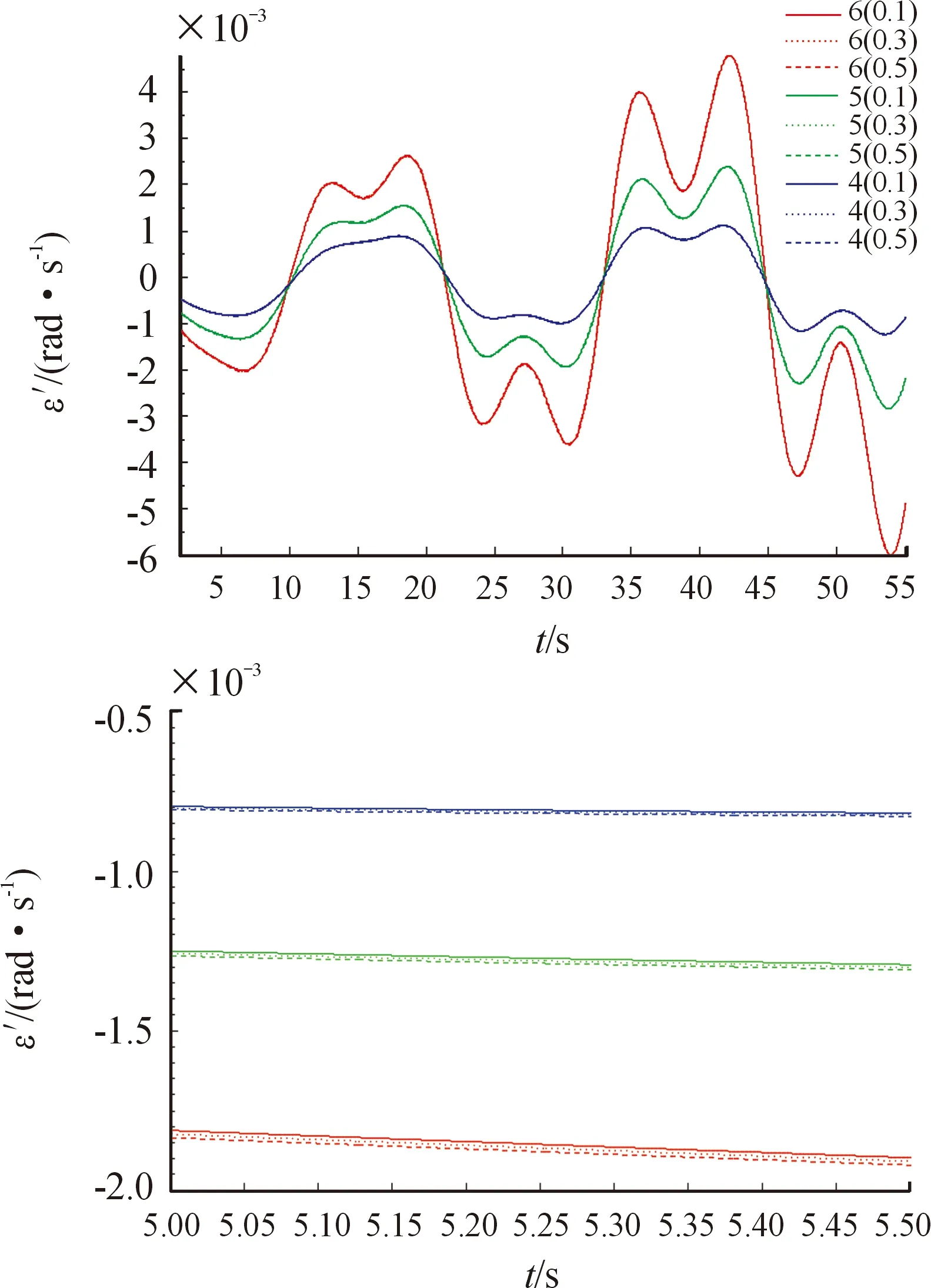
图3 质心高度变化的横摆速度对比

图2和图3表明,同一海况等级,当考虑侧向速度和横摆角速度为矢量时,随着质心高度的变化分2种情况:当速度为正时,随着质心高度的增加,侧向速度和横摆角速度均减小,当速度为负时,随着质心高度增加,侧向速度和横摆角速度均增加。考虑速度为标量时,速度与质心高度负相关。侧向速度和横摆角速度变化的趋势始终一致。当质心取值变化,随着海况等级的增加,侧向速度和横摆角速度产生波动程度随之增加。侧向速度对质心高度的变化更敏感。

3.2 质心纵向位置

质心纵向位置的变化,直接影响l1、l2的取值,分别将质心在标准值的基础上,前移和后移0.1 m,牵引车系统在不同海况下的侧向速度和横摆角速度变化如图4和图5所示(图4、图5中括号前面的数字代表海况等级,括号内数字1、2、3分别代表质心前移0.1 m、标准值、质心后移0.1 m)。

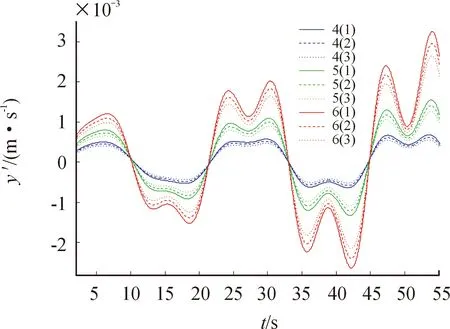
图4 质心纵向位置变化的侧向速度对比

图5 质心纵向位置变化的横摆角速度对比

图4和图5表明,同一海况等级,当考虑侧向速度和横摆角速度为矢量,随着质心纵向位置的前移,侧向速度和横摆角速度均呈增大的趋势。随着海况等级的增加,质心位置变化,侧向速度和横摆角速度产生波动程度随之增加。同样,侧向速度和横摆角速度变化的趋势始终一致,侧向速度对质心位置的变化更敏感。

为了能够找出影响程度的差异性,通过敏感度分析方法[27],以6级海况为例,计算侧向速度和横摆角速度对质心位置的敏感度。速度取仿真时间内的平均值,质心位置的变量均按照标准的数据正向增加取值,对比结果如表1所示。

表1 敏感度

根据表1可知,质心位置的变化与侧向运动参数的平均值呈反向变化,侧向速度对质心位置的变化更敏感,与仿真结果显示一致。侧向速度和横摆角速度对质心纵向位置的变化敏感度更高。根据敏感度分析可知:在进行牵引车结构设计和操纵稳定性优化时,如果对质心位置进行调整,需要以侧向速度为输出参考变量,优先考虑改变质心的纵向位置来达到优化的目的。