Asteroseismology of 16 Kepler Solar-like Stars: Stellar Parameters and the Effects of Element Diffusion

Shuai Wang and Qian-Sheng Zhang,3,4,5

1 Yunnan Observatories,Chinese Academy of Sciences,396 Yangfangwang,Guandu District,Kunming 650216,China;wangshuai@ynao.ac.cn,zqs@ynao.ac.cn

2 University of Chinese Academy of Sciences,Beijing 100049,China

3 Center for Astronomical Mega-Science,Chinese Academy of Sciences,Beijing 100101,China

4 Key Laboratory for the Structure and Evolution of Celestial Objects,Chinese Academy of Sciences,Kunming 650216,China

5 International Centre of Supernovae,Yunnan Key Laboratory,Kunming 650216,China

Abstract Element diffusion has small but significant effects on the structure of the stellar interior.It is interesting to investigate the effects of element diffusion using asteroseismology.We have constructed two grids of stellar models,one with diffusion and one without,for solar-like stars with masses between 0.9 and 1.4 solar masses,and varied initial helium abundance and metallicity.The oscillation frequencies of all stellar models have also been calculated.Piecewise Hermite cubic polynomials are adopted to interpolate stellar p-mode frequencies at an arbitrary age on a stellar evolutionary track.We have investigated 16 Kepler solar-like stars by comparing the model frequencies with observations.The suggested ranges of stellar parameters and some global variables are obtained.For all stars,the best model reproduces the observational frequencies with a χ2 of the order of unity.It has been found that element diffusion is important in modeling solar-like stars.Without diffusion,the best value of the initial helium abundance is below the primordial helium abundance from Big Bang nucleosynthesis.When diffusion is taken into account,the required initial helium abundance increases to be higher than the primordial abundance.Diffusion also generally improves the frequency fitting results by reducing the minimum of χ2.Investigation of the second difference of the oscillation frequencies on KIC 8694723 and KIC 10454113 indicates that the current model of element diffusion may underestimate the strength of settling.

Key words: asteroseismology–diffusion–stars: interiors–stars: abundances

1.Introduction

Asteroseismology is a powerful tool for probing physical processes in the stellar interior because the oscillation frequencies of stars are determined by the structure of the entire interior.As a result,asteroseismology is a reliable method for determining stellar parameters,such as mass,initial abundances,age,and global variables,including effective temperature,radius,depth of the convection zone,and rotation within the star (Chaplin &Miglio 2013).In this paper,we use the term stellar parameters only for the input parameters of the calculations of stellar models,and the term global variables for other stellar global variables.The period spacing ofg-modes can distinguish between hydrogen-and helium-burning red giant stars (Bedding et al.2011).The ratios of small to large frequency separations ofp-modes are sensitive to the stellar core and can be used to probe core overshoot mixing (e.g.,Deheuvels et al.2016;Zhang et al.2022).Solarp-mode frequencies have been used to constrain the properties of overshoot near the base of the convection zone because the oscillatory component in thep-mode frequencies is sensitive to the variation of the temperature gradient (Basu &Antia 1994;Christensen-Dalsgaard et al.1995,2011).The analysis of solarp-mode frequencies has revealed differential rotation in the solar envelope (Schou et al.1998).Investigation of mixed modes has shown fast core rotation in red giant stars (Beck et al.2012).

Element diffusion has been found to have small but significant effects on the structure of the interior of solar-like stars(Gai et al.2009;Deal et al.2020).This diffusion is driven by molecular diffusion,which causes hydrogen to concentrate toward the region of low pressure and low temperature(i.e.,the stellar surface),while helium and heavier elements concentrate toward the region of high pressure and high temperature (i.e.,the stellar core).In the solar interior,element diffusion leads to a settling of helium and a metallicity of approximately 10%,which improves the sound speed and density profile(Christensen-Dalsgaard et al.1991,1996).Another example is the depletion of Li abundance in solar-mass stars in open clusters,which occurs near the effective temperature of 6500 K(e.g.,Balachandran 1995;Jeffries 1997;Sestito et al.2004).This depletion is thought to be caused by element diffusion(Michaud 1986;Michaud &Charbonneau 1991).

On the other hand,it is common knowledge that molecular diffusion causes significant settling of helium and metallicity in stars with thin convective envelopes,such as those with a mass greater than 1.2 solar masses.However,the excessive settling of these elements does not align with observations of element abundances in A-and F-type stars (e.g.,Varenne &Monier 1999;Verma et al.2017,2019).To account for this,there are likely additional physical processes,such as radiative levitation (e.g.,Turcotte et al.1998;Dotter et al.2017;Deal et al.2018,2020) or dynamical mixing (Verma et al.2017,2019;Verma &Silva Aguirre 2019;Deal et al.2020),that compensate for the rapid settling of helium and metallicity in the stellar envelope.Combining molecular diffusion,radiative levitation,and rotational mixing has been shown to produce reasonable results for surface abundance and stellar parameters (Deal et al.2020).Investigating element diffusion using asteroseismology would be intriguing.Gai et al.(2009)explored the effects of element diffusion on the properties of oscillation frequencies in stellar models and discovered that diffusion causes the stellar models to evolve to lower large and small frequency separations in the asteroseismic diagram.

In this study,our focus is on 16 solar-mass stars observed by Kepler,where we investigate their stellar parameters and explore element diffusion using asteroseismology.Section 2 provides an introduction to the basic information on these stars.Section 3 outlines our study method,including the stellar modeling and calculations of the oscillation frequencies.The comparison of the model frequencies with observations is presented in Section 4,followed by discussions in Section 5.Finally,we summarize our main results in Section 6.

2.Target Solar-type Stars

To investigate element diffusion,we prefer to select mainsequence stars with many oscillation modes and low frequency uncertainties as our target stars.Red giants are not suitable for this study because their convective envelopes erase the effects of diffusion.We do not need to extract oscillation frequencies from the original Kepler database,so we select solar-like stars from published works.We estimate the mass of stars using the scaling relation (Kjeldsen &Bedding 1995) with the given large frequency separation Δν,frequency of maximum oscillation powerνmax,and effective temperatureTeff,and then select 16 stars with masses between 0.9 and 1.4 solar masses as our target stars.The oscillation frequencies of these stars have been obtained with high accuracy and published by Appourchaux et al.(2012) and Davies et al.(2016).These stars are all simple stars with only solar-likep-type oscillation modes and no mixed modes,which is convenient for interpolating model frequencies with stellar age.These stars have been investigated in asteroseismology by Metcalfe et al.(2014) and Silva Aguirre et al.(2015) (excluding KIC 8379927),and Martins et al.(2017) (for KIC 8379927).The asteroseismic fitting results of basic stellar parameters (mass,radius,abundances,and ages) are listed in Table 1.The effective temperatures for the stars in Appourchaux et al.(2012)are taken from Pinsonneault et al.(2012).In the study of Kepler solar-type stars by Metcalfe et al.(2014),helium diffusion and settling were taken into account,and the old GN93 solar mixture (Grevesse &Noels 1993) was adopted.The resulting initial helium abundances of some stars are close to the Big Bang nucleosynthesis (BBN) helium abundance.In the study of KIC 8379927 in Martins et al.(2017),a similarly low value of helium abundance was found,indicating that inappropriate properties exist in the stellar models.

Table 1Properties of the Target Solar-type Stars

3.Methods

3.1.Input Physics

The YNEV code (Zhang 2015) was used to calculate the stellar models and oscillation frequencies.The AGSS09 solar mixture (Asplund et al.2009) was adopted,with a～40%enhancement in Ne abundance (Young 2018),which is consistent with the most recent solar composition by Asplund et al.(2021).To interpolate the opacity in the high-temperature range,we used the OPAL opacity tables (Iglesias &Rogers 1996) based on the adopted mixture.For the lowtemperature range,we used the opacity tables by Ferguson et al.(2005).The OPAL equation-of-state tables (Rogers &Nayfonov 2002) were used to calculate the thermodynamic functions for given density,temperature,and abundances.The nuclear reaction rates were calculated using the NACRE fitting formulas (Angulo et al.1999) with a weak screening model(Salpeter 1954).Element diffusion driven by molecular diffusion with resistance coefficients based on screened Coulomb potential (Zhang 2017) was taken into account.The mixing length theory (MLT,Böhm-Vitense 1958) was used in the convection zones.Convective core overshoot was not considered in this work.

To compensate for the fast settling of helium and heavy elements in stellar models,we set an artificial efficient mixing in the envelope withlog(T/K) ≤ 5.9.This simulated extra mechanisms,such as turbulent mixing and radiative acceleration,that would compensate for the fast settling.This set led to a mixed envelope with about 5×10-4stellar mass for stars of 1.3 solar masses,consistent with the requirement for reproducing the helium glitch signature found in F stars by Verma &Silva Aguirre (2019).We set the base of the mixed envelope with a fixed temperature rather than a fixed mass fraction because radiative levitation,a major mechanism to compensate for the fast settling,is sensitive to temperature.This artificial mixing in the envelope withlog(T/K) ≤ 5.9did not affect the stellar models with masses lower than about 1.2 solar masses(depending on metallicity) because their convective envelopes were deeper thanlog(T/K) ≤ 5.9.

3.2.Stellar Models and Oscillations

We have computed two sets of model grids,one with molecular diffusion and one without.Each grid consists of approximately 10,000 stellar evolutionary tracks,with stellar parameters and steps outlined in Table 2.The parameter ranges cover the possible values for solar-mass stars,with the mixing length parameter αMLTranging around the solar calibration value of 1.8.The stellar models are evolved from the pre-mainsequence stage withTC=105K to the end of the mainsequence stage.Each evolutionary track,determined by a set of fixed stellar parameters,contains around 200 models in the main sequence,with typically 2000 mesh points.For all mainsequence stellar models on the grids,we have calculated the oscillation frequencies forl=0,1,2 in the range Max (Δν,νmax-15Δν)≤ν≤νmax+15Δν,whereνmaxis the frequency of maximum power and Δν is the large frequency separation,approximated as described in Kjeldsen&Bedding (1995):

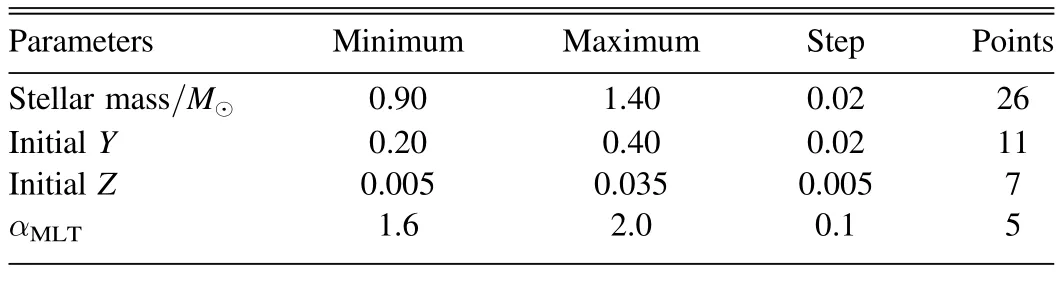
Table 2Stellar Parameters of the Grids

and

Stellar models are assessed by using the least χ2test.Here χ2is defined as

whereIi,modis the mode inertia and parametersc1andc3are determined by letting Equation (3) as a function ofc1andc3reach its minimum (Ball &Gizon 2014).

We use piecewise Hermite cubic polynomials to interpolate the oscillation frequencies νnlon each evolutionary track at an arbitrary induced stellar age τ=t/tms,wheretis the stellar age andtmsis the lifetime of the main-sequence stage of the stellar model.The involved derivativesdνnl/dτ are calculated using the Taylor expansion at five points of τ.This interpolation scheme allows us to avoid the issue of time resolution on stellar evolutionary tracks (see,e.g.,Wu &Li 2016).Similarly,the cubic spline interpolation scheme on stellar age has been adopted in Li et al.(2020).The Hermite interpolation has two advantages over the cubic spline.First,it is local,meaning that the interpolated value is determined only by the adjacent mesh points,while the cubic spline is nonlocal and the interpolated value is affected by the variation of all mesh points and a supplement of mesh points.Second,the accuracy of the Hermite interpolation can be improved theoretically by using higher-order polynomials.The interpolation scheme works well forp-mode oscillations.However,near the end of the main sequence,mixed modes may appear,and the interpolation scheme may lead to intermediate errors for the frequencies of the mixed modes,especially for avoided-crossing mixed modes.This is not a fault of the interpolation scheme,but rather due to the time resolution of the stellar model not being sufficient to trace avoided crossing well.If the time step of the stellar model were shorter,the interpolation scheme would work well on the mixed modes.However,this is not necessary in this work because the target stars are all simple,meaning that no mixed modes appear.For a set of given values of the stellar parameters and given observational frequencies,we use χ2on the evolutionary track to assess the stellar parameters.The minimum of χ2can be searched for by iterations on τ.

To interpolate frequencies for stellar models on an evolutionary track,we can use the frequencies of models with even/odd model numbers to estimate the frequencies of models with odd/even model numbers.By comparing these estimated frequencies to the original model frequencies,we can determine the interpolation errors.Figure 1 shows the distribution of errors for all models.We found that the typical relative rms error for all stellar models is about 0.01%,and the maximum error is less than 0.03% in cases without mixed modes.Since the resulting errors already include random errors in the model frequencies,we set the final relative error(including both random and interpolation errors) of the model frequencies in Equation (3) to 0.01%.

Figure 1.Distribution of errors of the Hermite interpolation on oscillation frequencies without mixed modes.

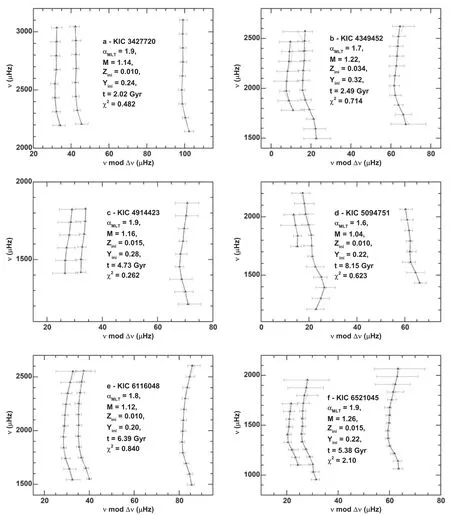
Figure 2.Échelle diagrams for six stars:KIC 3427720,KIC 4349452,KIC 4914423,KIC 5094751,KIC 6116048,and KIC 6521045.The observational modes are represented by gray circles,and the error bars have been enlarged by a factor of five for visibility.The black triangles represent oscillation modes with frequencies(adjusted for surface correction)from the best stellar model with element diffusion.The stellar parameters and χ2 of the best models are also shown.Each panel links modes with the same l by a line,with the leftmost line corresponding to l=2,followed by l=0 and l=1.

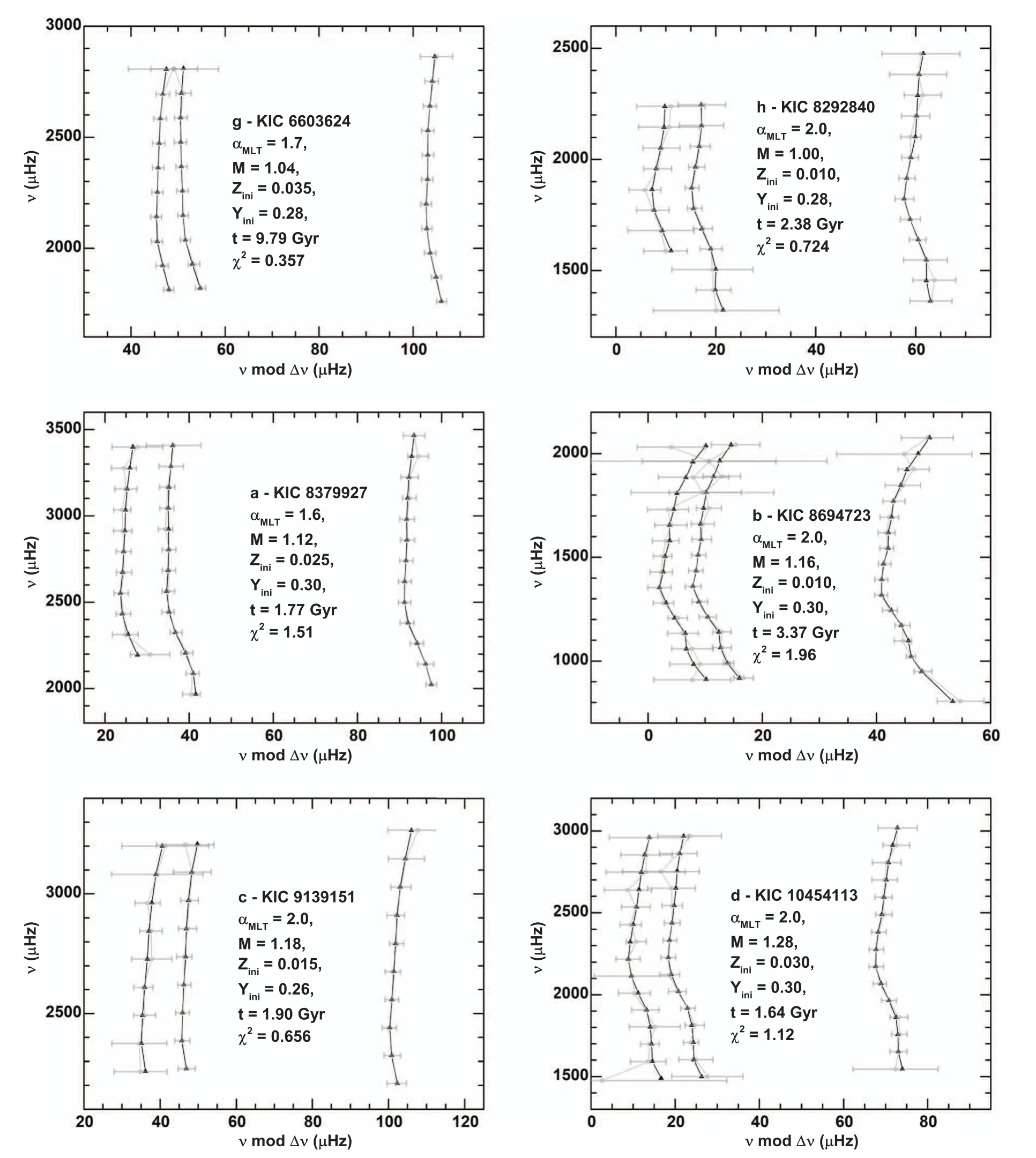
Figure 3.Similar to Figure 2,but for KIC 6603624,KIC 8292840,KIC 8379927,KIC 8694723,KIC 9139151,and KIC 10454113.

Figure 4.Similar to Figure 2,but for KIC 10963065,KIC 11133306,KIC 11295426,and KIC 12009504.

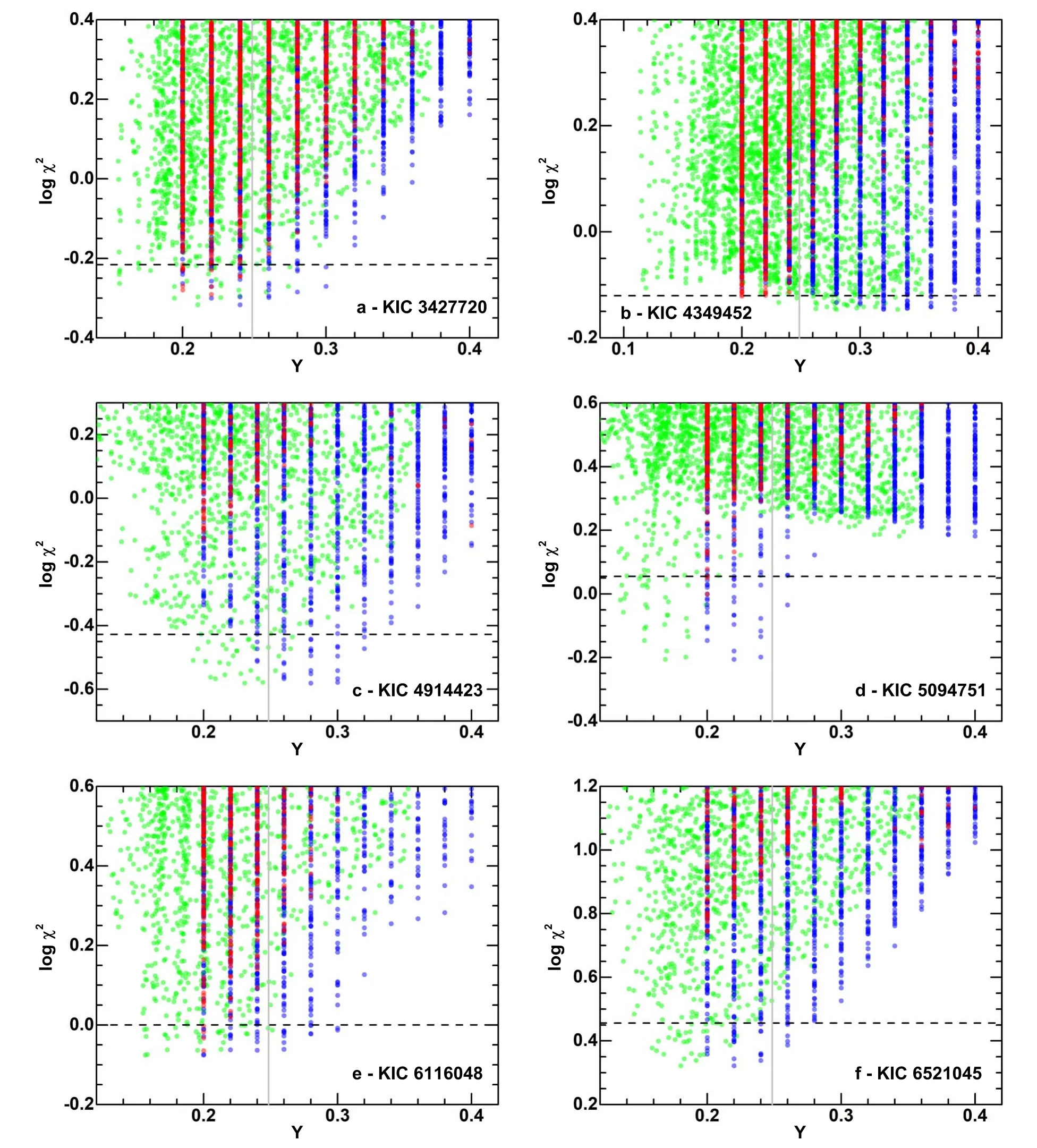
Figure 5.Helium abundances versus log χ 2 for KIC 3427720,KIC 4349452,KIC 4914423,KIC 5094751,KIC 6116048,and KIC 6521045.The red dots represent Yini=Ys of the stellarmodels w ithoutmolecular diffusion,while the blue dots represent Yini of the stellar modelswithmolecular diffusion.Thegreen dots represent Ys of the stellarmodelsw ith molecular diffusion.Each circle on the graph corresponds to the best model w ith aminimum of χ2 on a stellar evolutionary track in the model grids.The vertical gray lines show the BBN primordial helium abundance,which is Yp=0.2485 according to Cyburt et al.(2008).The horizontal lines indicate the suggested ranges for the models with diffusion,which is the range covered by the dots below the horizontal line.

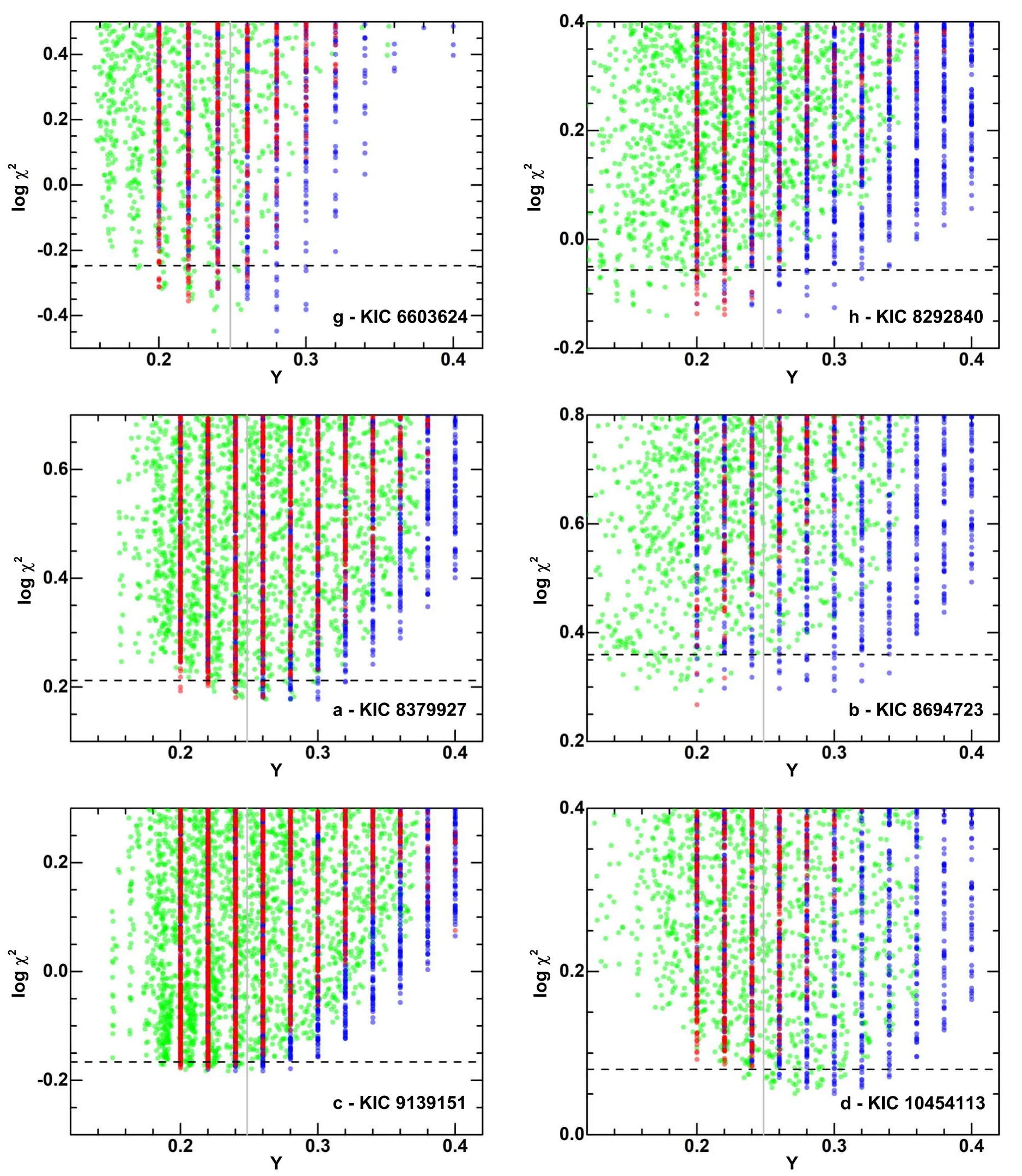
Figure 6.Similar to Figure 5,but for KIC 6603624,KIC 8292840,KIC 8379927,KIC 8694723,KIC 9139151,and KIC 10454113.

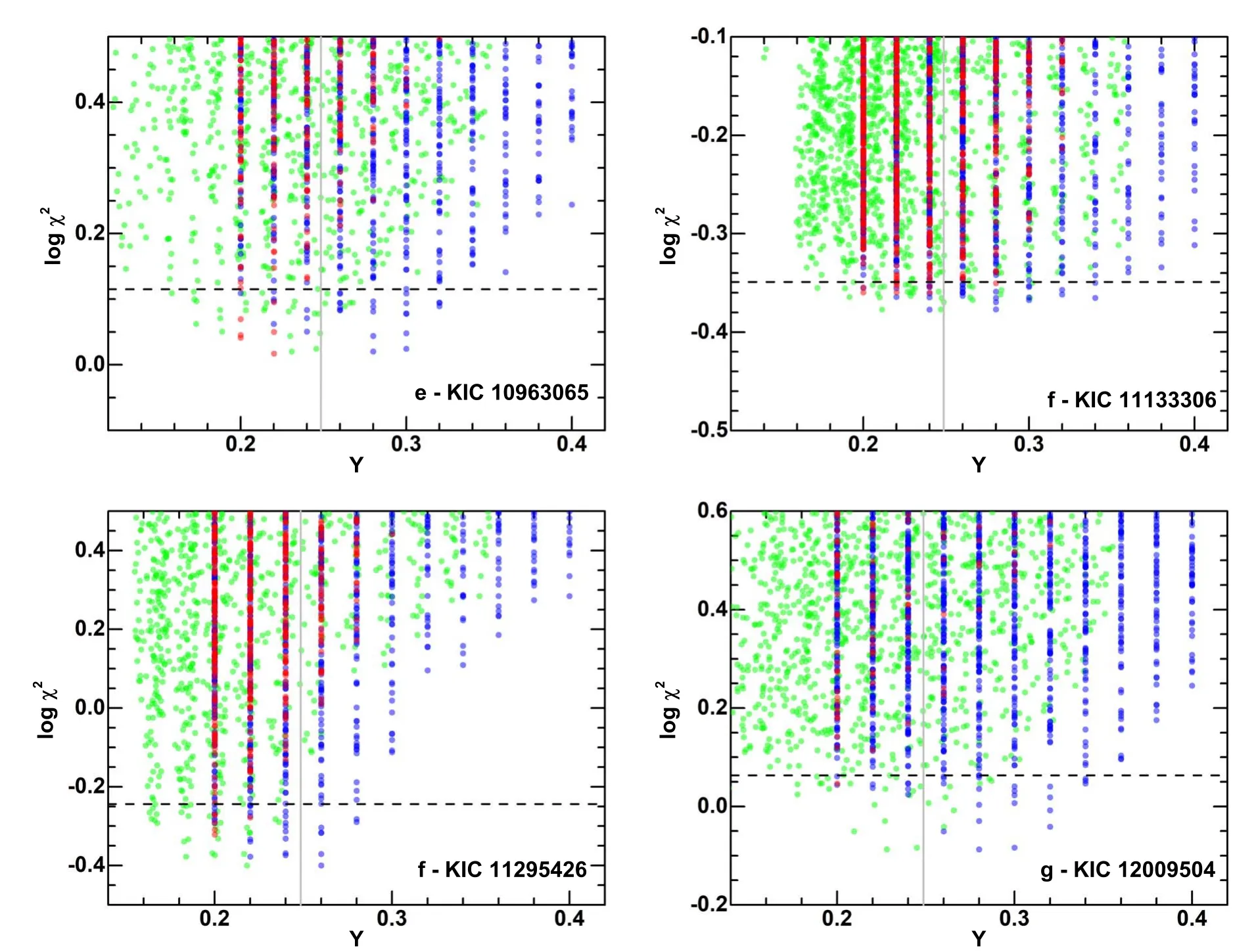
Figure 7.Similar to Figure 5,but for KIC 10963065,KIC 11133306,KIC 11295426,and KIC 12009504.

The database of stellar models can be considered as an asteroseismic database for solar-like stars.By comparing the observational frequencies of a solar-like star with the frequencies of all stellar models in the database,we can quickly determine χ2and analyze the stellar parameters.In the traditional method,many stellar models have to be calculated to model a single target star.Our approach significantly improves the efficiency of basic asteroseismic studies of solarlike stars because the asteroseismic database can be directly used to compare the model frequencies with the observational frequencies of a new target star without any calculation of stellar models.

4.Result

4.1.Global Variables of Target Stars

We can calculate χ2for each star using all the evolutionary tracks on the grids.The best overall stellar model is the one with the lowest χ2.Figures 2–4 show the échelle diagrams of the best model in the diffusion grid for all target stars,taking into account surface correction.It is evident from these figures that the best models accurately reproduce the observedp-mode oscillation frequencies,as the χ2values for all best models are around unity.

To estimate the parameter ranges,statistical methods such as singular value decomposition (Brown et al.1994;Metcalfe et al.2009) or likelihood functions based on χ2(Giammichele et al.2016) are commonly used.However,these methods require variables to be independent,which is not the case for stellar oscillation frequencies.Although the measurements of oscillation frequencies are independent,theoretically they are determined by the complex structure of the star and are correlated with each other due to the asymptotic approximation.Therefore,we use an empirical method in this study to estimate the parameter ranges.We select the 30 best models with the lowest χ2for each star as candidate models.The suggested ranges for the effective temperatureTeffin kelvin,radiusRin solar radius,massMin solar masses,agetin gigayears,central hydrogen abundanceXc,and radius fraction of the base of the convective envelopeRbc/Rare determined by these candidate models.We tested a larger sample of 50 candidate models and found that the resulting parameter ranges were enlarged by 10%–20%.The suggested ranges for each star are listed in Table 3,with two rows for each star: the upper row represents the stellar model with element diffusion,while the lower row represents the stellar model without element diffusion.

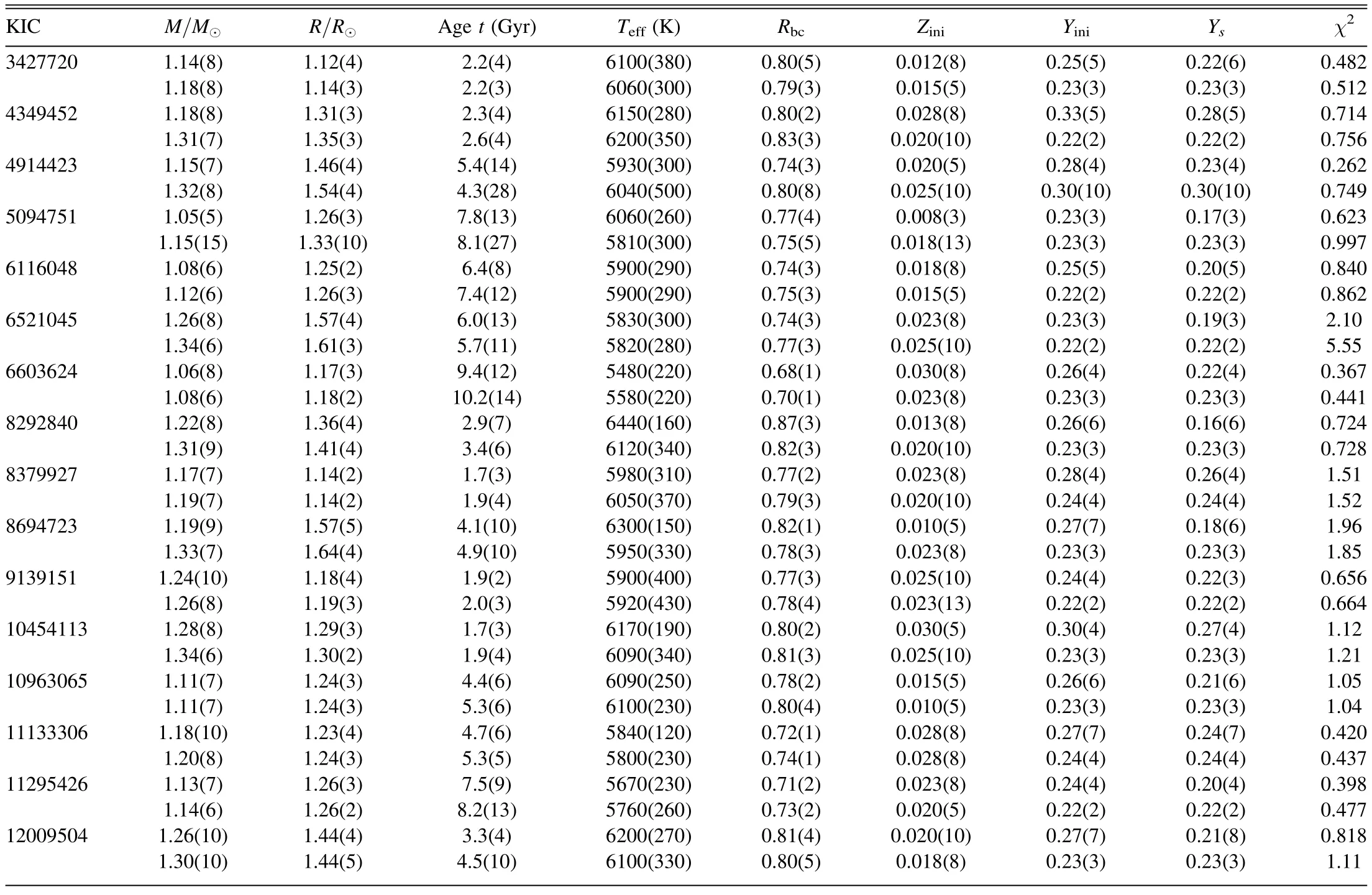
Table 3Global Variables of the Target Solar-like Stars

When comparing Table 3 to Table 1,we can see that our results for global variables are consistent with those of Metcalfe et al.(2014)and Silva Aguirre et al.(2015).However,there are significant differences in the masses of KIC 6521045,KIC 8694732,and KIC 12009504.Our results show higher stellar masses for these stars than Metcalfe et al.(2014) and Silva Aguirre et al.(2015).This could be due to the fact that the range of stellar mass in Silva Aguirre et al.(2015)is limited to 0.7–1.2 solar masses.The suggested masses for KIC 8292840 and KIC 12009504 in our results are consistent with Deheuvels et al.(2016),who found stellar masses of 1.17(5)solar masses for KIC 8694732 and 1.30(7)solar masses for KIC 12009504.This comparison confirms the validity of the asteroseismic model database we constructed in this study.Our database can be used to quickly obtain stellar parameters for new mainsequence solar-mass stars with asteroseismic observations.

4.2.Helium Abundances with and without the Molecular Diffusion

The most intriguing analysis involves comparing the results of the stellar models that incorporate element diffusion with those that do not.Our primary focus is on the abundances,as they are directly influenced by diffusion.The initial helium abundance is constrained by the BBN primordial helium abundance,which serves as a benchmark for evaluating the stellar models.

Figures 5–7 illustrate the relationship between χ2and the initial helium abundanceYiniand surface helium abundanceYs.Notably,in the absence of diffusion,the bestYinivalues for all stars are lower than the BBN primordial helium abundance ofYp=0.2485 (Cyburt et al.2008),as indicated by the vertical lines.Conversely,Yinivalues in the presence of diffusion are consistently higher than those without diffusion for all stars.All suggested ranges ofYiniwith diffusion encompass the rangeYini＞Yp.Another significant finding,as shown in Table 3 and Figures 5–7,is that the overall minimum of χ2is generally reduced when diffusion is considered,except for KIC 8694723 and KIC 10963065.Those results clearly show the necessity of element diffusion in modeling solar-mass stars.

The reason why the best values ofYiniincrease when element diffusion is taken into account needs to be investigated.Solar-likep-mode oscillations propagate in the form of sound waves with the adiabatic sound speedwhereTis the temperature and μ is the mean molecular weight.SinceTis much higher in the stellar core than in the envelope,the propagation time of sound waves is mainly determined by the structure of the envelope.Thus,the structure of the envelope,especially μ determined byYs,should be correlated with thep-mode frequencies.This analysis is supported by the numerical results shown in Figures 5–7,where for all target stars except KIC 4349452 and KIC 10454113,the distribution ofYs=Yiniin the case without element diffusion is basically the same asYsin the case with element diffusion because the best values ofYsin the two cases are close to each other.Since diffusion leads to helium settling,Yini＞Ys,andYiniin the case with diffusion increases to produce the requiredYsto match the observational frequencies.

In this work,molecular diffusion has been partially compensated by artificial mixing in the envelope with log (T/K) ≤ 5.9.However,we have checked the best models of all target stars and found that in every case from the zero-age main sequence to the age of the best model,the bottom of the convection zone is always hotter than 105.9K,except for several stars with masses larger than 1.2 solar masses.The minima of the temperature at the base of the convective envelope in those stars are higher than 105.8K,which is slightly lower than 105.9K.Therefore,the results are minimally affected by the artificial mixing.

5.Discussions

5.1.The Second Differences of Frequencies as a Probe of Element Diffusion

Based on the theory of stellar oscillation developed by Tassoul (1980) and the variational method (see,e.g., Montgomery et al.2003),changes in the sound speed profile of a star model can affect its oscillation frequencies.Gough(1990) discovered that an acoustic glitch,caused by helium ionization,a convective boundary,or element diffusion,can create an oscillatory component in thep-mode frequencies.This component has a period of 2τc,g,where τc,gis the acoustic depth of the glitch and τcis defined as

This knowledge has been used to detect helium ionizations(Houdek &Gough 2007),determine the depth of the convection zone(Christensen-Dalsgaard et al.1991),and study convective overshoot(Christensen-Dalsgaard et al.2011)in the Sun.The oscillatory component of thep-mode frequencies caused by an acoustic glitch can be described using the second differences of frequencies,δ2νn,l=νn-1,l-2νn,l+νn+1,l(Gough 1990).

The lower boundary of the convective envelope in solarlike stars is affected by an acoustic glitch due to the variation in temperature gradient.When considering element diffusion,this creates an abundance gradient below the base of the convective envelope,which can enhance the glitch due to the relationship between sound speed and temperature.This can strengthen the oscillatory component ofp-mode frequencies,as demonstrated in Gai et al.(2009) using the Fourier transform of δ2νn,l.In this study,we examine the impact of element diffusion on the observed frequencies of KIC 8694723 and KIC 10454113,which have the most observation frequencies.Figure 8 shows the second differences of models and observations for both stars.For KIC 8694723,the model with diffusion exhibits clear oscillatory components in the second differences,while the model without diffusion does not.Although there are significant uncertainties,the observational second differences also show clear oscillatory components for ν ＞1700 μHz.For KIC 10454113,the two models with and without element diffusion have similar strengths of oscillatory components in the second differences.However,the observational second differences show stronger oscillatory components,particularly forl=2 modes.As demonstrated by Gai et al.(2009),Fourier analysis of the second differences can aid in understanding the oscillatory component.We calculated the Fourier spectrum of the amplitudes of the second differences of the stellar models and observations using the formula

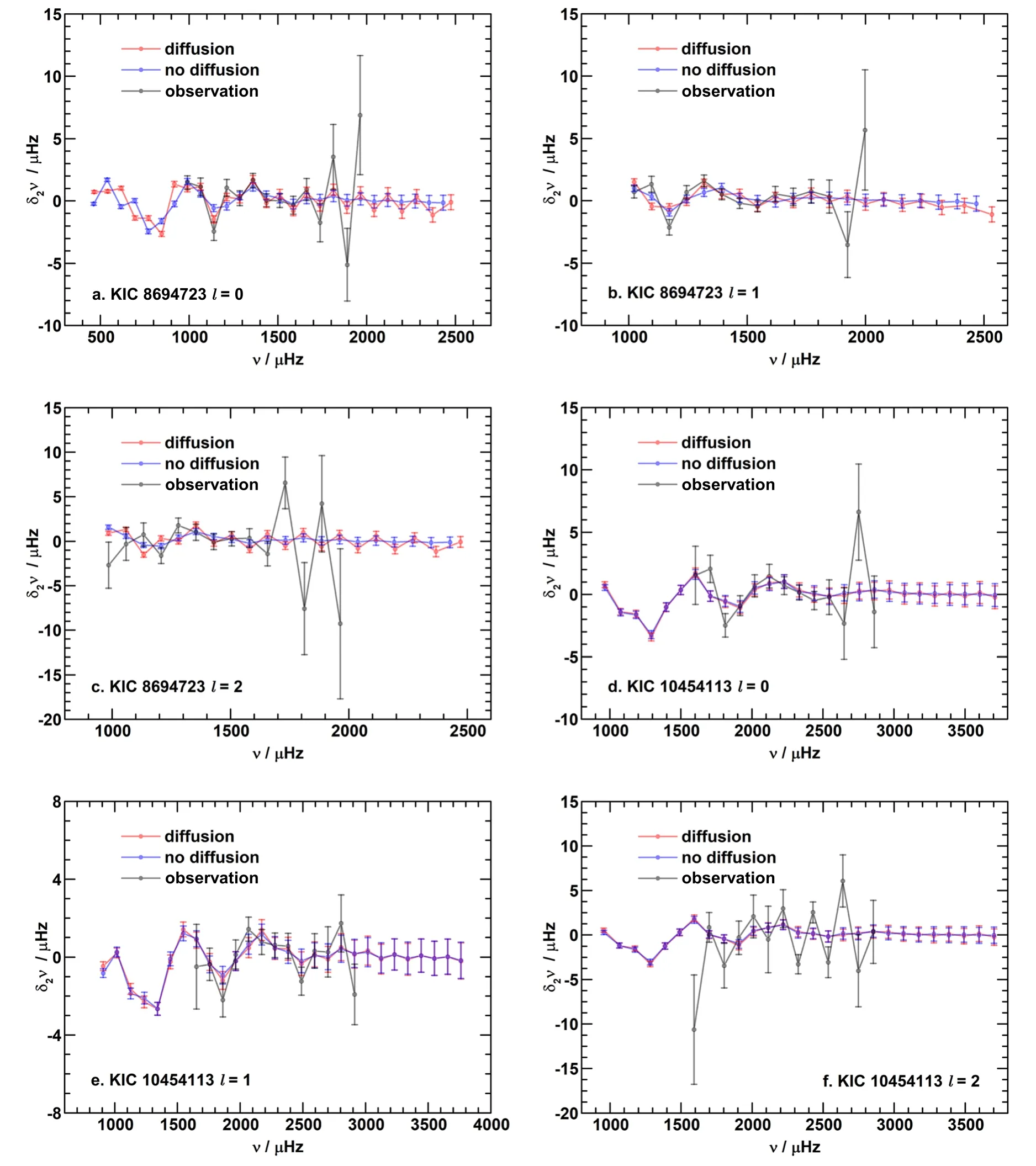
Figure 8.Second differences of the p-mode frequencies.For KIC 8694723,the parameters of the stellar model with diffusion are same as those of Figure 3(b),and the parameters of the stellar model without diffusion are as follows: αMLT=1.6, M=1.32 M⊙, Yini=0.20, Zini=0.015,and t=4.91 Gyr.For KIC 10454113,the parameters of the stellar model with diffusion are same as those of Figure 3(d),and the parameters of the stellar model without diffusion are as follows:αMLT=1.7,M=1.32 M⊙, Yini=0.24, Zini=0.025,and t=1.76 Gyr.

whereNis the number of data points and the samples are τk=100ks,and shown in Figure 9.The side lobes of the Fourier spectrum are significant due to the small sample size of the second differences,especially for the observations.For KIC 8694723,the peaks of the spectrum for the stellar models are located at around 2500 s and 7000 s,while for KIC 10454113,they are located at around 1600 s and 5000 s.In both cases,the peak at low τ is caused by He ionizations,and the peak at high τ is caused by the convective boundary,which is enhanced by element diffusion.The acoustic depth of the glitches of He ionizations and the convective boundary is shown in Figure 10,and it can be observed that the peak of the spectrum is located at twice the acoustic depth of the glitch.The difference between KIC 8694723 and KIC 10454113 is that diffusion leads to a much stronger glitch in KIC 8694723 but has little effect in KIC 10454113.This explains why the second differences or their spectrum for the two KIC 10454113 models,with and without element diffusion,are basically identical,as shown in Figures 8 and 9.The reason for the difference between KIC 8694723 and KIC 10454113 is that KIC 8694723 is older than KIC 10454113,so diffusion leads to stronger settling of helium and heavy elements,as shown in Figure 11.

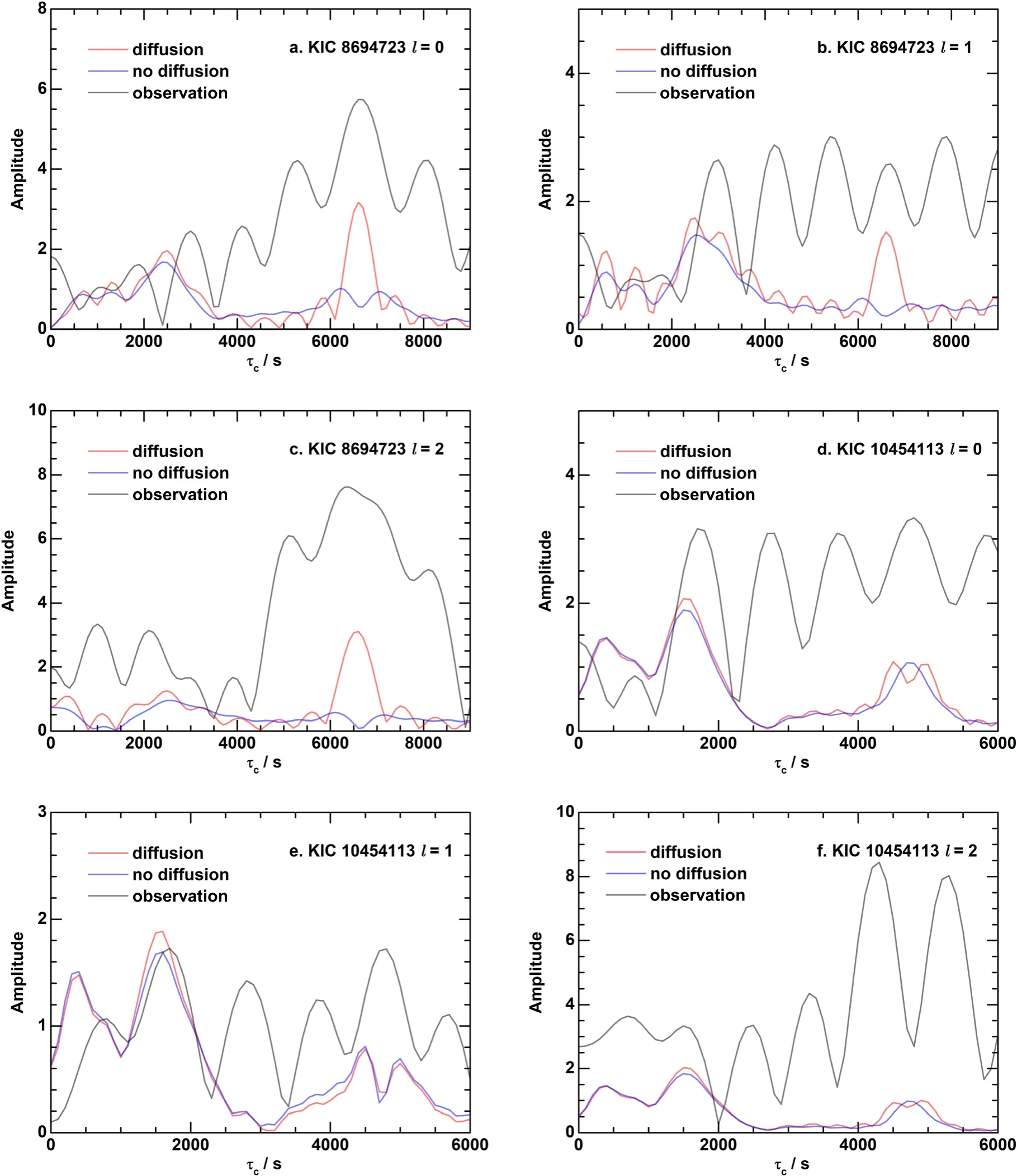
Figure 9.Fourier spectrum of the second differences of the p-mode frequencies shown in Figure 8.

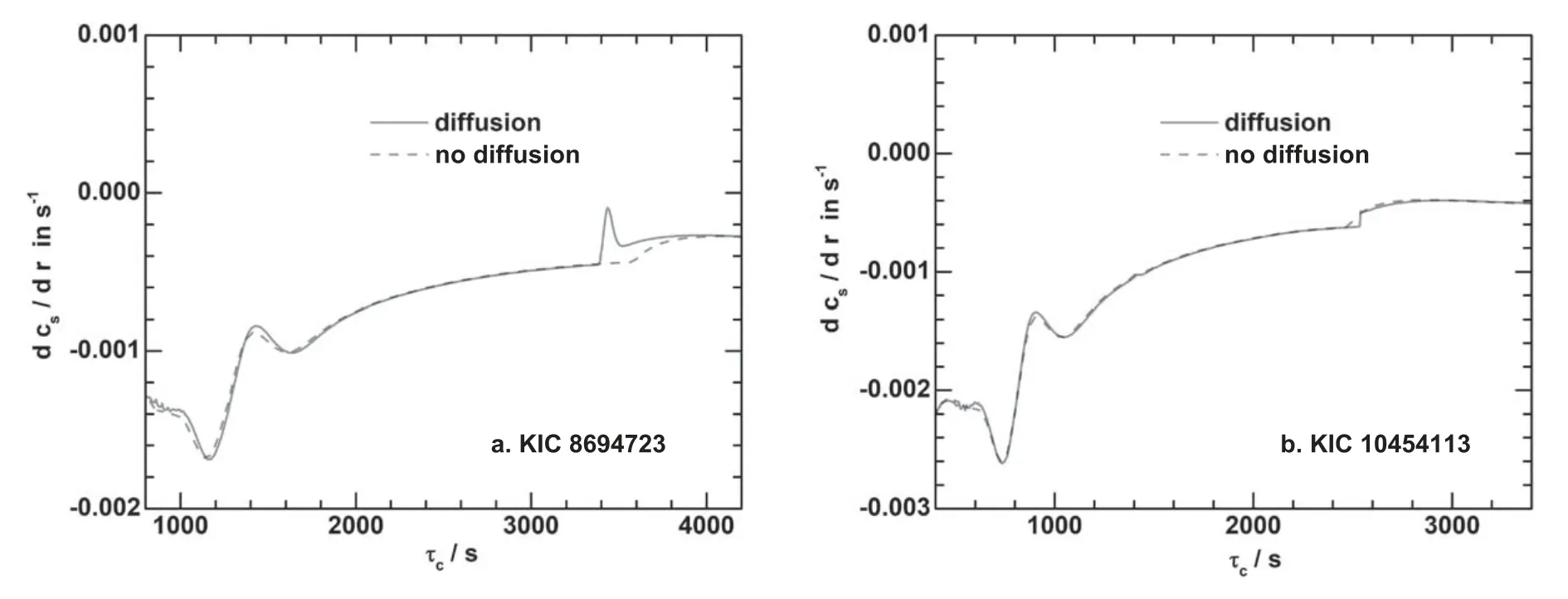
Figure 10.The derivatives of sound speed in the stellar envelope of the stellar models mentioned in Figure 8.The bumps at 1000 s ＜τ ＜2000 s in the left panel and at 800 s ＜τ ＜1100 s in the right panel are caused by He II and He I ionization.The glitches at τ=3600 s in the left panel and at τ=2600 s in the right panel are caused by the convective boundary and element diffusion.

Figure 11.The hydrogen abundance profiles near the base of the convective envelopes of the stellar models.The abscissa is the acoustic depth.

The most interesting result shown in Figure 9 is that the spectrum of the observational second differences also shows peaks at twice the acoustic depth of the convective boundary.However,the amplitudes are several times larger than the model amplitudes.Similarly,it is also directly shown in Figure 8 that the observational second differences show stronger oscillatory components than the stellar models.These indicate that the current theoretical model of element diffusion may underestimate the effect of settling.However,it should be emphasized that more observational data are required to confirm this indication.

Enhancing the strength of element diffusion in the solar model has been adequately discussed.Although modified element diffusion cannot solely solve the “solar model problem”(Zhang 2014),it is shown that enhanced element diffusion could alleviate the inconsistency of the sound speed profile between the standard solar model and the helioseismic inversions (Guzik et al.2005;Yang &Bi 2007;Yang 2016,2019,2022).On the other hand,the asteroseismic investigation on a pulsating extremely low-mass white dwarf has constrained the abundance profile(Su&Li 2023),and it is different from the profile predicted by the current theoretical model of element diffusion.Therefore,it would be interesting to investigate more asteroseismic data of solar-like stars to better understand element diffusion in stellar interiors.

5.2.Limitations

One limitation of our stellar models is the absence of convective core overshoot,which could result in systematic errors in our results.As Roxburgh &Vorontsov (2003) found,the ratios of small to large frequency separations are sensitive to the structure of the stellar core,and convective core overshoot can be analyzed by examining these ratios(see,e.g.,Deheuvels et al.2016;Zhang et al.2022,and references therein).However,in this study,we focus on the oscillation frequencies themselves.The sound wave spends most of its time in the stellar envelope,where the sound speed is low,making the oscillation frequencies more sensitive to the envelope’s structure.Therefore,the presence of convective core overshoot should not significantly affect our results.In future work,we plan to investigate overshoot by modeling more target stars in an extended stellar model grid with varied overshoot parameters.

6.Summary

In this paper,we calculated the oscillation frequencies and stellar models for a mass range of 0.9 to 1.4 solar masses,both with and without molecular diffusion.However,for stars with a mass greater than 1.2 solar masses,molecular diffusion causes helium and metallicity to settle too quickly,which is inconsistent with observations.To compensate for this,we introduced a mixed envelope withlog(T/K) ≤ 5.9to simulate radiative levitation and dynamical mixing.The oscillation frequencies are interpolated on the stellar age using piecewise Hermite cubic polynomials,allowing for the determination of frequencies at any age.The models are then used to investigate the effects of diffusion on 16 Kepler mainsequence solar-like stars,all of which are simple and do not exhibit mixed modes,allowing for accurate frequency interpolation.

We created a small asteroseismic database for mainsequence solar-mass stars,which includes the oscillation frequencies near the empirical frequency of maximum power for all models.This database can be used to obtain stellar parameters for a new target star without having to calculate stellar models and oscillation frequencies,making it more efficient than traditional asteroseismic study schemes.The database and source code have been uploaded to https://github.com/Swhonghong/model-grid-and-data.git.

Based on a comparison of model frequencies with observationalp-mode frequencies of target stars,it has been found that the models fit well within suggested ranges of stellar parameters.The best model for each star shows a low value of χ2with an order of magnitude of unity,as seen in the échelle diagrams of Figures 2–4.Table 1 lists suggested ranges for stellar parameters (M,Zini,Yini) and important global variables(Teff,R,t,Xc,Rbc/R).

The effects of molecular diffusion were analyzed by examining the dependence of χ2onYiniandYs.When diffusion is absent,the requiredYinifor the best fit is lower than the BBN primordial helium abundanceYpfor all target stars.However,when diffusion is taken into account,the requiredYinisignificantly increases to higher thanYp,while the overall minimum of χ2is generally reduced.Therefore,it is concluded that molecular diffusion is necessary in modeling solar-like stars to avoid too low aYinithat conflicts with the BBN primordial helium abundance.

The second differences of oscillation frequencies for KIC 8496724 and KIC 10454113 were also discussed.Observational second differences show stronger amplitudes on the Fourier spectrum than the stellar models at the base of the convective envelope,indicating that the current model of element diffusion may underestimate the strength of settling.However,more asteroseismic data of main-sequence solar-like stars with high precision are required to support this.

Acknowledgments

Many thanks to the anonymous referee for providing valuable comments which improved the original version.Funding for Yunnan Observatories is co-sponsored by the National Key R&D Program of China (Grant No.2021YFA1600400/2021YFA1600402),the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB 41000000),the National Natural Science Foundation of China(Grant Nos.1177064 and 12133011),the Foundation of the Chinese Academy of Sciences (Light of West China Program and Youth Innovation Promotion Association),the Yunnan Ten Thousand Talents Plan Young and Elite Talents Project,and International Centre of Supernovae,Yunnan Key Laboratory (No.202302AN360001).