中国区域大气加权平均温度的多因子精化模型

刘费帆,张露露,黄玲,黄良珂,刘立龙

(1.桂林理工大学 测绘地理信息学院,广西 桂林 541006;2.桂林理工大学 旅游与风景园林学院,广西 桂林 541006)

0 引言

近年来,在大气科学与气象学领域应用全球导航卫星系统(global navigation satellite system,GNSS)来进行反演大气可降水量(precipitable water vapor,PWV)得到了快速的发展,与传统大气探测相比,GNSS反演具有全天候、成本低、时空分辨率高和分布范围广等优势,广泛应用于各种天气和灾害的检测与预报[1-3]。水汽是地球大气层中最活跃的元素,与降水关系紧密,GNSS通过对流层天顶湿延迟(zenith wet delay,ZWD)乘以水汽转换系数(∏)来反演PWV[4],其中大气加权平均温度(Tm)是水汽转换的一个重要参量,其计算的精度直接决定PWV的精确程度[5]。因此构建更精确的Tm模型成为了许多学者的研究热门。

Tm计算模型主要分为两类。第一类是基于实测的气象参数采用回归分析等方法建立的;第二类是用局部地区或全球数年的Tm数据直接拟合成不需要气象参数的经验模型。目前较为经典和常用的是使用Bevis公式来计算Tm,Bevis等[6]利用北美地区(27°N～65°N)探空站的8 718个资料建立了Tm与地表温度Ts之间的线性关系模型(Tm=0.72Ts+70.2)。该模型只有两个参数,使用简单且精度较好,但因系数具有季节和地理的限制,所以应用在其他地区误差会增大,需要重新拟合系数,对此众多学者展开了相关研究[7-8]。莫智翔等[9]利用回归分析方法建立了中国西部地区的Tm模型,模型对西部地区有着更好的适用性和稳定性。朱海等[10]根据陕西的气候类型并顾及纬度和周期建立了分区域的Tm模型,解决了回归模型在不同气候区的适应性问题,并与Bevis模型比较,精度提升了44.9%。王晓英等[11]对中国分气候区研究发现,地基GPS数据拟合的Tm-Ts模型系数与气候关系明显并具有集群性。

由于Bevis模型系数具有较强的地域性,在整个中国区域精度表现较差,无法满足高精度GNSS PWV反演的迫切需求。本文先根据2015—2017年的探空数据拟合计算出了适合中国地区的Bevis系数。在Tm与Ts具有较强的相关性的基础上,进一步分析发现Tm与水汽压具有较强的相关性且表现出随季节变化的周期性,同时相关研究表明Tm具有明显的地理分布特性,由于我国地域辽阔,地形复杂多样,因此模型构建时又顾及了经纬度和高度的影响。为进一步提高模型的适用性,按照地理分区将中国地区分为北方地区、南方地区、西北地区和青藏地区,分别建立了4种不同地理分区的Tm模型,并用2018年的探空数据对区域模型的精度进行分析验证。Landskron等[12]提出了一种全球对流层延迟格网经验模型(GPT3模型),该模型不仅提供气压、水汽压、Tm等气象参数,还提供东西和南北方向的对流层水平梯度信息,是目前全球最先进的对流层延迟格网经验模型。该模型使用简单,只需要用户输入相应测站的坐标和年积日,即可获得该测站的各类气象参数,故可以用作参考模型来进行对比分析。

1 数据来源及Tm计算方法

1.1 数据来源

本文采用的是美国怀俄明大学网站(http://weather.uwyo.edu/upperair/sounding.html)所提供的2015—2018年中国区域81个探空站的实测数据,时间分辨率为12 h。使用2015—2017年的数据来建模,2018年的数据作为参考值来验证。中国区域81个探空站的分布情况如图1所示,不同的地理分区如图例所示。

图1 中国地区81个探空站的位置分布

1.2 Tm计算方法

利用数值积分法对每个测站上空的水汽压和气温进行积分,表达如式(1)所示[13]。

(1)

式中:es为该测站上空的水汽压,单位为hPa;T为绝对气温,单位为K;h为测站高度,单位为m;z为测站上空的垂直高度,单位为m。

该计算方法获得的Tm值精度高且气象误差影响较小[14-15]。由于水汽压不能通过实测手段获得,可利用式(2)计算。

(2)

式中:q为比湿;P为气压,单位为hPa。

2 中国区域Tm多因子精化模型建立

2.1 影响因子的相关性分析

在GNSS反演PWV的研究中,许多学者已经得出Tm与Ts、水汽压es的自然对数、高度都具有较好的线性相关性。利用2015—2017年探空站数据分析的结果也表明,Tm与其都具有良好的线性相关关系,如图2(a)、图2(b)、图2(c)所示。Tm与地理位置有一定的关系(由于太阳高度角θ的大小)[16],故本文又加入了经度和纬度影响因素,使新模型更符合中国的实际情况,经纬度的相关性如图2(d)、图2(e)所示。

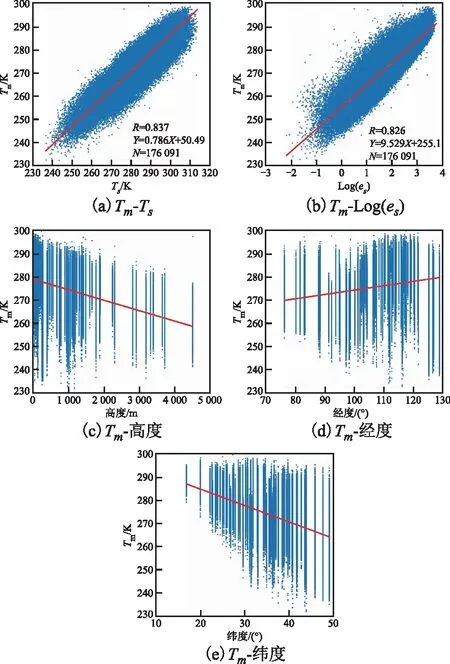
图2 Tm与Ts、es、高度、经纬度的相关性分析

由图2可知Tm与Ts、es的自然对数和经度都呈现正相关关系,其中Ts和es的自然对数相关性较强,相关系数都大于0.8,所以在建模时需要考虑这3个因子。由图2可知,Tm与高度和纬度表现为负相关关系,因此,建模也需要考虑这两个因子的影响。

2.2 Tm多因子精化模型的建立

Bevis公式的系数具有明显的地域性,需要重新对系数进行拟合。本文根据中国地区2015—2017年的探空站数据,计算出中国区域精化后的Bevis模型(Tm-B模型),如式(3)所示,求取的α1、α2系数值分别为0.79和50.5。

Tm=α1×Ts+α2

(3)

由文献[13]可知,Tm随季节表现为周期性的变化。为了探讨Tm随季节的变化情况,以桂林探空站(57957)为例,绘制了2015—2018年的Tm变化曲线,如图3所示。

图3 桂林探空站Tm时间序列

由图3可知,Tm存在明显的季节周期性,而线性函数的拟合会平滑掉大部分周期,从而导致误差。本文参考Yao等[17]的研究可知,Tm的残差序列存有明显的周期性,为研究其季节的变化情况,选取桂林探空站(57957),首先,建立Tm与Ts的一次关系式,然后,将其计算的Tm值与桂林探空站实测的Tm值相减获得残差值,结果如图4所示。

图4 桂林探空站Tm残差时间序列

由图4可知,Tm残差也具有一定的周期性,所以需要对原模型进行补偿来改善计算结果的准确性,本文采用具有年周期和半年周期的三角函数来建模,以此来提高模型的精确度。结合上述的影响因子,建立了一种新的Tm模型关系式,如式(4)所示。

Tm=β1cos(2π×doy/365.25)+β2sin(2π×doy/365.25)+β3cos(4π×doy/365.25)+β4sin(4π×doy/365.25)+β5Ts+β6×h+β7×φ+β8×λ+β9×loges+β10

(4)

式中:h为测站高度;φ、λ为经纬度;doy为年积日;β1～β10为模型系数。

本文利用中国地区的81个探空站2015—2017共3年观测数据中的大气加权平均温度、地面温度、水汽压、测站高度和经纬度来确定新模型的各个系数。首先,利用数值积分的方法计算出中国地区每个探空站的Tm值,然后带入相应的Ts、es、高度和测站经纬度数据,利用最小二乘原理拟合计算出Tm-C模型的各个系数值,结果如表1所示。

表1 使用中国地区2015—2017年的探空数据计算的Tm-C模型的系数

为验证Tm-C模型对Tm残差周期性的补偿,将Tm-C模型与桂林探空站Tm-Ts模型计算的Tm值与其探空站的实测值做差进行对比,如图5所示。可以看出,Tm-C模型的残差值相对于Tm-Ts模型误差较小且较为集中,对Tm的计算结果的准确性具有一定的改善作用。

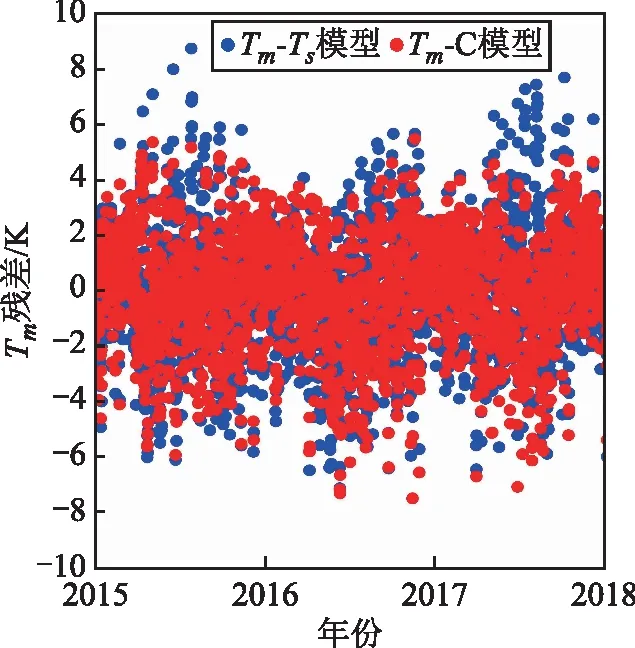
图5 桂林探空站不同模型的Tm残差序列对比

由于中国地域辽阔,地形复杂多样,按照整个中国地区建模影响因子可能会被平滑掉,为进一步提升Tm-C模型的精度,将中国区域按照图1地理分区分为4个部分,每个区域各自建模,依次得到Tm-N、Tm-S、Tm-W和Tm-Q模型,使用的是式(4)的模型。对处于不同区域的探空站进行归类,利用2015—2017年的探空资料得到不同地理分区的区域模型,模型系数如表2所示。

表2 使用中国地区2015—2017年的探空数据计算的4个地理分区模型的系数

3 Tm精化模型精度验证

使用2018年中国区域探空资料计算的Tm值作为参考值,来检验模型精度,采用偏差(bias)和均方根误差(root mean squared error,RMS)来衡量新模型精度的标准。

3.1 多因子Tm模型精度验证

为评定Tm-C模型的精度,以2018年全国81个探空站资料计算得到的Tm值作为参考值,来检验Tm-C模型的精度,并与Bevis模型、Tm-B模型和GPT3模型进行对比。将不同模型计算出的Tm值与对应的参考值进行比较,统计出不同模型的年均bias和RMS值,结果分别如表3、图6和图7所示。

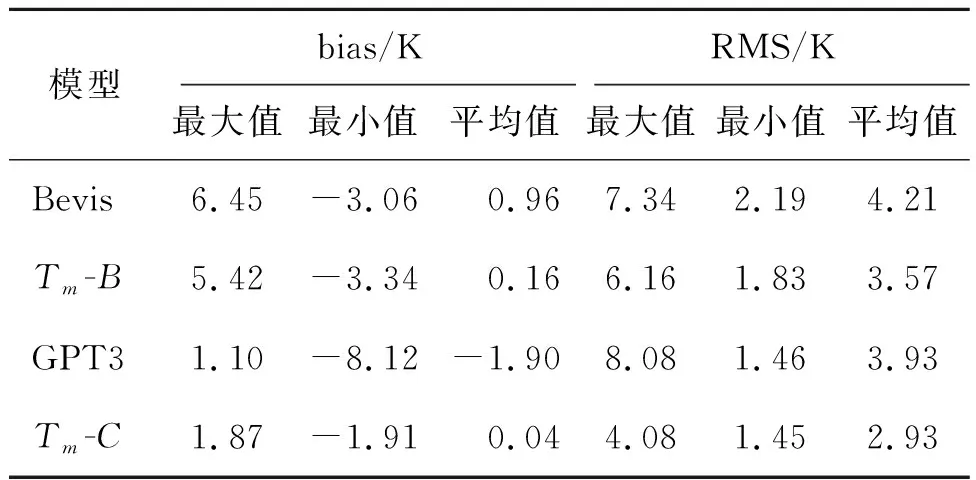
表3 利用2018年探空站资料检验不同Tm模型的精度对比

图6 利用2018年探空站资料验证不同模型的年均bias分布

图7 利用2018年探空站资料验证不同模型的年均RMS分布

由表3可知,在中国区域内,Bevis模型的正偏差值最大,GPT3模型的负偏差最大,二者的变化范围相差为9 K。对于年均偏差值,除了GPT3模型为负偏差值,其余3个模型均为正偏差值,其值依次为0.96 K、0.16 K、-1.9 K和0.04 K。其中,Tm-C模型的年均偏差值和变化范围最小,且偏差的最大值和最小值的绝对值基本相等,说明顾及多因素的Tm-C模型的稳定性最好。对于RMS值,Bevis模型的RMS值最大,为4.21 K,而Tm-C模型的RMS值最小,为2.9 K,说明Tm-C模型精度优于其余3个模型。而由中国区域探空站数据拟合的Tm-B模型相对于原Bevis模型则有较大的提升,提升了0.64 K(15.2%),表明基于本地数据建立的Bevis模型比北美地区的Bevis模型可靠性更高。GPT3模型RMS平均值为3.93 K,相对于Bevis模型精度较高,但比中国区域精化的Tm-B模型精度小。Tm-C模型精度最优,相对于Bevis、Tm-B和GPT3模型,精度分别提高了1.28 K(30.4%)、0.64 K(17.9%)和1 K(25.4%),说明Tm-C模型计算出的Tm值具有较好的精度。由图6发现,Bevis模型在西北地区和青藏地区具有较大的正偏差,而基于中国地区数据建立的Tm-B模型较Bevis模型则有一定程度地降低,二者在中国南部区域均显示出较小的偏差,在-3～0 K之间,GPT3模型总体上表现为负偏差,而Tm-C模型在整个中国区域内显示出较小的偏差和稳定性。根据图7显示,Bevis模型在青藏地区的RMS值为6 K左右,在北方和西北地区RMS值在3～6 K之间,而在南方地区的RMS值为3 K左右。Tm-B模型有一定程度的降低,但变化幅度仍然较大,其原因主要是因为中国地区的纬度跨越大及高程起伏大和没有考虑Tm残差周期变化所导致的。GPT3模型RMS值整体在2～5 K之间变化,但在高海拔地区RMS值较大(6 K以上),原因在于GPT3是经验模型和未考虑Tm高程归算。Tm-C模型在北方和西北地区RMS值为3 K左右,在南方和青藏地区RMS值在3 K以下,部分地区则为1 K左右,Tm-C模型总体RMS误差较小,说明对整个中国地区有较好的适应性。

为进一步提高Tm-C模型的精度,本文将整个中国区域按照地理分区分为4个部分,每个区域各自建模,依次得到Tm-N、Tm-S、Tm-W和Tm-Q模型,以2018年的探空资料计算值作为参考,与Bevis和Tm-C模型进行对比分析,得到各模型的bias和RMS值,如表4和图8所示。

表4 利用2018年探空站数据来验证4个地理分区模型的精度

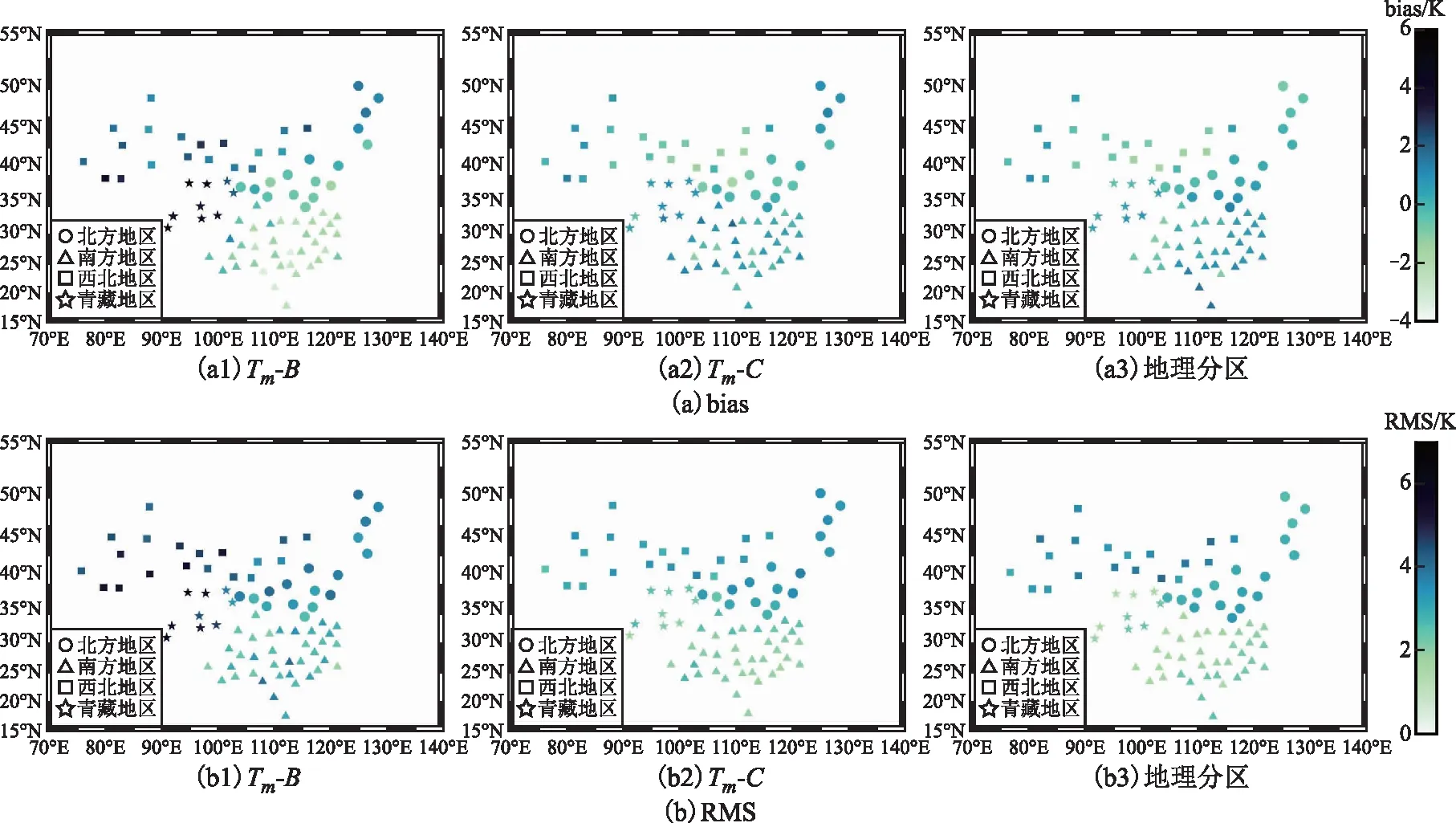
图8 使用2018 年探空站资料验证不同模型地理分区的bias和RMS分布

由表4可知,4个地区Bevis模型均表现出最大的偏差值,其最大偏差在青藏地区,为6.45 K,且变化的范围也较大。Tm-C和4个地理分区模型的偏差值较小,且偏差的正负值基本相等,表明模型计算的数值与参考值基本接近,精度较高。RMS值方面,Bevis模型依旧表现为最大的误差,中国区域的Tm-C模型应用到各个地理分区RMS值有一定范围的上下浮动,其最大RMS值为3.63 K。而按照地理分区的Tm-N、Tm-S、Tm-W和Tm-Q模型则表现为更小的RMS值,相比于Tm-C模型分别提高了0.67 K(18.5%)、0.53 K(21.4%)、0.59 K(16.5%)和0.64 K(24.6%),表明地理分区的模型能进一步提高中国地区的Tm精度。为进一步分析分区域建模的优越性能,因以上分析已证明Tm-B与Tm-C模型相较于Bevis与GPT3模型精度显著提高,故将Tm-B与Tm-C模型与分区域建模进行对比分析,如图8所示。

由图8(a)可以看出,Tm-B模型的bias精度最低,地理区域的模型只有南方和西北地区的部分点的偏差的绝对值在1～2 K左右,大部分中国地区的偏差的绝对值在0～1 K,表明分地理区域的模型相比于全国Tm-B和Tm-C模型具有更好的稳定性。由图8(b)可知,Tm-B模型在青藏和西北地区的RMS值为4～6 K,Tm-C模型较Tm-B模型精度有一定的改善,地理分区的模型则进一步提升,在西北地区的RMS值为3.5 K左右,北方地区RMS值为3 K左右,南方和青藏地区的RMS值为2 K左右,与Tm-B和Tm-C模型相比每个地理分区的精度都有一定程度的提升,表明按地理分区的Tm模型较Tm-B和Tm-C模型适应性和稳定性更好。

3.2 Tm对GNSS-PWV计算的影响

因大多数GNSS基准站与探空站不并置,且大部分GNSS基准站并未安装大气气象传感器,导致PWV反演较为困难。故建立中国区域和地理分区的Tm模型可增加GNSS反演PWV的精度。本文使用文献[13]提出的GNSS-PWV计算方法,表达如式(5)所示。

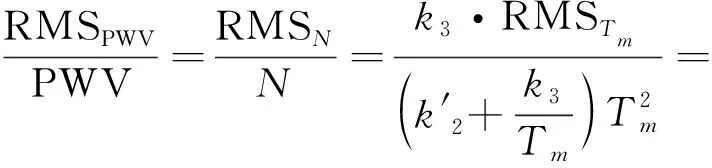
(5)

表5 2018年中国地区不同模型计算PWV的理论RMS和相对误差的精度对比

4 结束语

1)本文利用2015—2017共3年81个探空站数据,在分析Tm与各个影响因子的相关性基础上,建立了顾及温度、水汽模型,并与2018年的探空资料对比,具有较好的精度,Tm-C模型的bias和RMS值分别为0.04 K和2.93 K。

2)将Tm-C模型与Bevis模型、使用中国区域数据拟合的Tm-B模型以及GPT3模型对比,bias值和RMS值分别提升了95.8%、75%、97.9%和30.4%、17.9%、25.4%,表明在中国区域内顾及多因子的Tm-C模型精度更高、稳定性更强。为进一步得到高精度的Tm信息,按照地理分区将中国地区划分为北方、南方、西北和青藏4个地区,与Tm-C模型相比,RMS值分别提升了18.5%、21.4%、16.5%和24.6%。