基于GAUNet的深度学习相位解缠方法

李东旭,谢先明

(1.广西科技大学 自动化学院,广西 柳州 545006;2.广西科技大学 电子工程学院,广西 柳州 545006)

0 引言

相位解缠(phase unwrapping,PU)作为众多干涉测量技术的核心步骤,广泛应用于干涉合成孔径雷达、光学干涉测量、核磁共振成像等领域[1]。从干涉测量技术中得到的相位主值会被限制在(-π,π]区间内,通过对相位主值加上整数倍的相位周期来恢复原始相位的处理过程称为相位解缠。目前传统相位解缠算法主要分为路径跟踪类算法[2-5]、最小范数类算法[6-9]、非线性滤波类算法[10-11]3类。路径跟踪类算法的代表性方法包括质量引导法、枝切法、网络流法等,这类方法通过设置合适的积分路径来阻止误差沿全局蔓延,在高信噪比区域可达到较好的解缠精度,然而在低信噪比区域易造成噪声误差沿路径传递的现象,且该类方法受积分路径的影响往往会比较耗时。最小范数类算法的代表性方法包括无权最小二乘法和加权最小二乘法等,与路径跟踪法理念不同,该类方法通过建立恰当的代价函数,使解缠相位梯度与缠绕相位梯度之间差异最小化来估算解缠相位,当干涉图中的噪声较小时,能够具有较强的稳健性和较快的运算速度,而当干涉图噪声较大时则会平滑解缠结果,容易丢失相位细节信息和降低解缠相位的动态范围。非线性滤波类算法的代表性方法包括卡尔曼滤波方法、粒子滤波方法等,这些方法通过建立干涉相位的贝叶斯递推估计程序来解缠,与上述两类方法相比,非线性滤波类算法具有较好的噪声抑制能力,能够获得较高的解缠精度,但这类方法存在耗时较长的问题。传统相位解缠方法均可在一定程度上取得较好的解缠效果,但其在解缠效率方面仍有待提升。因此,如何高效地从缠绕相位中提取出真实相位仍是当下所需解决的关键问题。

深度学习(deep learning,DL)被广泛应用于语音识别、图像识别、自然语言处理等领域,并在目标识别、图像分类、图像分割和自然语言处理等不同领域的许多问题中都展现出显著优势。近年来,DL技术已开始应用于干涉图相位解缠领域,各种基于DL的相位解缠算法[12-20]相继被提出,这些方法大致可分为3类。第一类是两步PU法,首先将干涉图相位解缠问题转化为语义分割问题,利用语义分割来预测干涉图缠绕相位的模糊数,随后将预测模糊数与缠绕相位相结合,并通过适当的后处理程序来获取无模糊的解缠相位,如PhaseNet、Segnet、DeeplabV3+等。第二类是一步PU法。这类方法采用神经网络直接从缠绕相位中提取解缠相位,无需任何后处理步骤。如DLPU、PU-M-Net、U-Net、U-Net3+等。第三类是把深度学习神经网络与传统算法相结合来提高干涉图相位解缠精度,如PGNet、BCNet等。与传统相位解缠方法相比,上述基于DL的PU方法具有解缠效率较高的特点,但其噪声鲁棒性以及解缠相位的准确性仍需进一步提高。

本文提出了一种基于全局注意力上采样(GAU)的相位解缠算法(简称为“GAUPU”),该算法将PU-M-Net网络和注意力机制进行了有效融合,通过建立缠绕相位与解缠相位的非线性映射关系来达到一步相位解缠的目的。首先,在编码-解码路径之间采用了一种注意力模块,即全局注意力上采样模块,将低级特征层和其对应的高级特征层进行连接,GAU模块可以有效利用多尺度特征映射,并利用高级特征为低级特征提供加权指导,从而进一步增强干涉图条纹特征信息;其次,PU-M-Net所采用的跳跃连接操作促进了相位细节信息与语义条纹信息的有效融合,提高了相位解缠中初始特征的利用率;最后,根据干涉图噪声量级评估系统对噪声干涉图划分为4个噪声量级,构建4个噪声量级的数据集对网络模型进行训练,完成训练后的网络能直接从不同量级下的缠绕相位中获得解缠相位。实验结果表明本文网络具有较高的解缠效率以及鲁棒性。

1 基于深度学习的神经网络相位解缠模型

GAUPU大致实现途径如下:Ⅰ)搭建适合干涉图缠绕相位解缠的网络架构,利用文献[18]提出的干涉图噪声量级评估系统对干涉图的噪声量级进行划分,并构建多组不同噪声量级的训练集,对同一深度学习网络架构进行训练得到适用不同噪声量级干涉图解缠的解缠网络,如图1(a)所示;Ⅱ)对待解缠的干涉图进行噪声量级判定,随后将其匹配至对应噪声量级的预测网络进行解缠,如图1(b)所示。

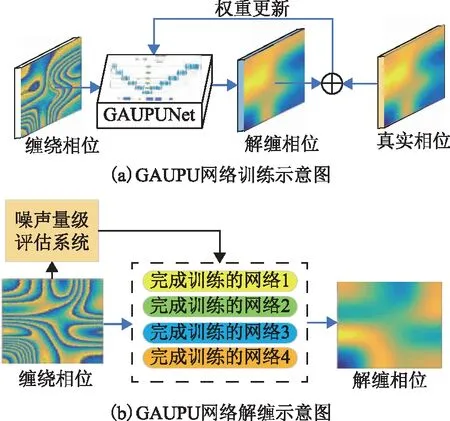
图1 GAUPU流程示意图

1.1 GAUPU网络模型

GAUPU网络由文献[16]所述PU-M-Net网络以及GAU模块组成,该网络结构如图2所示,其中网络上方的数字为通道数。首先,左侧编码路径利用6个基本模块由上至下逐层提取输入的缠绕相位图的特征信息,每层模块的输入部分由不同分辨率的原始输入特征图与上一层基本模块的输出特征通过跳跃连接①相结合得到初始特征,并将该特征通过跳跃连接②与依次经过卷积层(如图中白色[C],Conv3×3层+批量归一化BN+激活函数Relu)和残差网络层(如图中橙色[R])所得到的特征图进行融合,融合后的特征图通过卷积层进行卷积操作得到基本模块的输出特征,而后使用2×2最大池化将得到的输出特征压缩到下一个尺度,所使用的卷积填充操作采用相同(same)模式,利用这种模式使得卷积前与卷积后的特征尺度保持不变,编码路径最终输出的特征图用于解码路径的输入,右侧解码路径的网络架构与编码路径对称,其基本模块与编码路径中的模块相同,每个模块的输入由GAU模块(如图中绿色GAU)生成的特征图以及经过2×2上采样的下一层的输出特征通过跳跃连接③连接构成,该路径亦利用6个基本模块由下至上逐渐恢复到原始输入特征图大小。最后,通过跳跃连接④将解码路径中每层模块的输出进行合并,并利用卷积核为1×1的卷积层调整特征图通道数以此获取最终的输出结果。

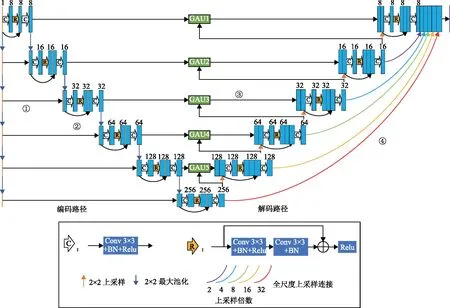
图2 GAUPU网络框架

由于低级特征在空间分布与物理意义上存在差异,很难有效利用低级特征,为了提升低级特征的利用率,在编码-解码跳跃连接中采用了注意力机制GAU的连接方式,即将高级特征的全局注意力嵌入到低级特征中。采用这种方式具有如下优势:低级特征在保留相位信息的同时融入了高级特征的上下文信息,弥补了高级特征与低级特征之间的差距,有利于更好地提升性能;不会显著增加网络参数;能够高效地适应不同尺度下的特征映射;本文注意力机制先进行全局池化,后进行压缩感知进而稀疏表达,在保留语义信息的同时可较好地减少计算和储存成本。

GAU的结构如图3所示,其中:C1、H1、W1分别代表低级特征的通道数、高和宽;C、H、W分别代表高级特征的通道数、高和宽;r为衰减因子(本文取r=8)。以图2中GAU3为例,首先对解码路径输出得到的分辨率为64×64的特征图执行全局平均池化操作得到全局上下文信息,并采用瓶颈门控设计的方法[21]进一步提取解码路径高级特征的上下文信息,得到包含高级特征全局上下文信息的注意力特征,即先采用卷积核为1×1的卷积层对特征图的通道数进行降维为64/r,再用卷积核为1×1的卷积层对上述得到的特征图进行升维操作,其输出的通道数与编码路径的低级特征通道数保持一致。其次,将注意力特征与编码路径得到的低级特征相乘,得到加权后的低级特征。最后,采用残差设计的方法将经过上采样的高级特征与加权后的低级特征进行融合。

图3 GAU结构示意图

在深度学习框架keras2.4.3的基础上训练网络,计算机主要配置参数为Inter Xeon W-2245(3.9 GHZ)+128 GB RAM,NVIDIA Geforce RTX 3080 GPU。网络训练采用自适应矩估计优化器、均方误差损失函数,初始学习速率为0.001,训练轮数为160,最小训练批次为6,训练时间约为32 h。值得注意的是,虽然网络训练较为耗时,然而完成训练后的DL网络执行干涉图相位解缠的时间耗费几乎是可以忽略不计的。

1.2 噪声量级评估系统

利用文献[18]提出的干涉图噪声量级评估系统对干涉图的噪声量级进行划分,并构建多组不同噪声量级的训练集,对同一深度学习网络架构进行训练得到适用不同噪声量级干涉图解缠的解缠网络。

根据干涉图噪声估计值把干涉图相位噪声划分为4等级,如表1所示。

表1 噪声等级划标准

噪声估计值Ne计算方法如式(1)所示。

(1)

式中:M和N分别为干涉图的行数和列数;Res(x,y)为取模运算后的残差图;l为噪声加权系数(本文取值l为100);W(x,y)为利用伪相干系数法获得的干涉图质量图。

对待解缠的干涉图进行噪声量级判定,随后将其匹配至对应噪声量级的预测网络进行解缠,有利于提高干涉图相位解缠精度。

1.3 网络数据集

构建4组不同噪声量级的训练集,对同一深度学习网络架构进行训练得到适用不同噪声量级干涉图解缠的解缠网络。各噪声量级的数据集均包含35 000组数据,按如下4种方式生成。

方式1:按文献[14]所述的数据集构建方法产生3 000组数据,其图像尺寸为256×256,标签图像相位范围为0～60 rad。

方式2:按文献[15]所述的数据集构建方法产生4 000组数据,其图像尺寸为256×256,标签图像相位范围为0～60 rad。

方式3:由山西省大同市、安徽省黄山市、浙江省金华市等地区DEM数据转化InSAR干涉相位图数据24 000组,即先把DEM数据根据InSAR理论转换为真实干涉相位,随后产生添加不同噪声的缠绕相位图,共产生24 000组InSAR干涉图数据,其图像尺寸为256×256,标签图像相位范围为0～60 rad。

方式4:由传统相位解缠方法所获得的InSAR干涉相位图数据3 000组,即利用传统相位解缠方法对实测InSAR干涉图解缠获得其解缠相位,随后产生添加不同噪声的缠绕相位图,共产生3 000组准实测InSAR干涉图数据,其图像尺寸为256×256,标签图像相位范围为0～60 rad。

2 干涉图相位解缠实验分析

2.1 模拟干涉图相位解缠实验

为了验证GAUPU网络架构的性能,利用该网络算法解缠不同类型的模拟干涉图,并与质量引导算法(QGPU)、枝切法(BUTPU)、迭代最小二乘法(ILS)等传统相位解缠算法作比较。模拟干涉图如图4所示,图4(a)、图4(b)分别为多峰地形、金字塔真实相位,分辨率均为256×256,图4(c)、图4(d)分别为图4(a)、图4(b)真实相位所对应的噪声缠绕图,其信噪比依次为4.94 dB、-1.07 dB,所对应的噪声等级依次为1、3。

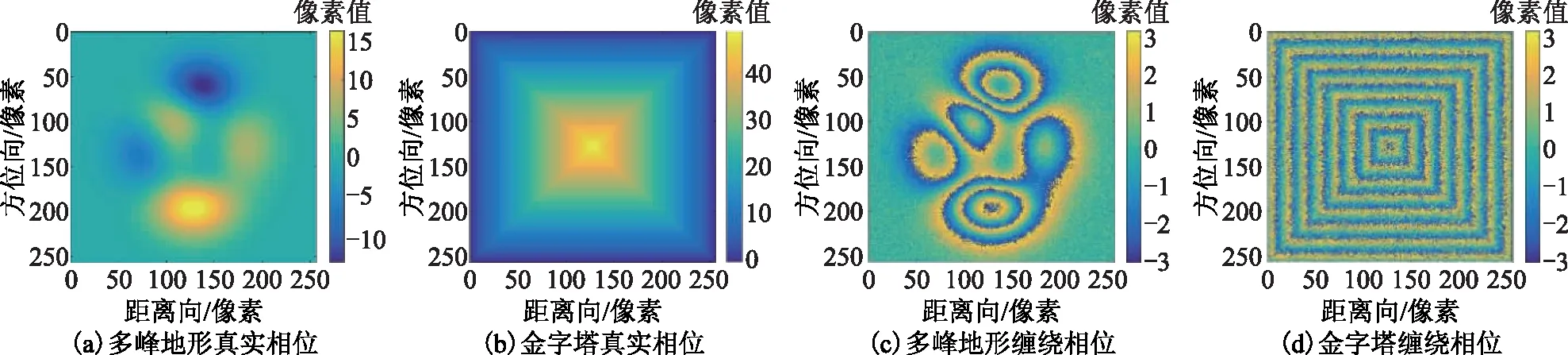
图4 模拟干涉图

利用QGPU、BUTPU、ILS、GAUPU分别对图4(c)、图4(d)进行解缠,其解缠结果依次对应图5、图6,图5、图6分别为上述算法对应图4(c)、图4(d)的解缠相位图、解缠相位误差图以及解缠相位误差直方图。从图5可看出,QGPU、BUTPU、ILS 3类传统算法在干涉图信噪比较高时均可取得较好的解缠结果。从图6可观察到在低信噪比情况下,QGPU在解缠过程中出现噪声误差沿质量引导路径蔓延,造成解缠相位不一致,甚至解缠失败的情形;BUTPU解缠时易造成“孤岛”现象;ILS解缠相位大致连续,但其误差范围较大。与此同时,GAUPU算法能够取得较为理想的解缠结果,且误差范围较小,特别是当干涉图所含噪声较大时,其误差范围要远远小于上述3类方法,表明该方法具有较好噪声鲁棒性的同时能够较为完整地还原干涉图相位信息。表2列出了上述方法解缠不同信噪比干涉图的均方根误差(30次实验平均),可以看出随着信噪比的降低,GAUPU解缠精度要远优于QGPU、BUTPU、ILS 3种算法。表3列出了上述算法解缠图4(c)、图4(d)所示干涉图的平均时间耗费。可以看出,GAUPU时间耗费要远远小于上述其他3种算法。故与QGPU、BUTPU、ILS算法相比,GAUPU不仅取得了较为稳健的解缠效果,而且在时间消耗方面亦具有明显优势。其中,QGPU、BUTPU、ILS的运行环境均为MATLAB R2016b,GAUPU的运行环境为python 3.8。

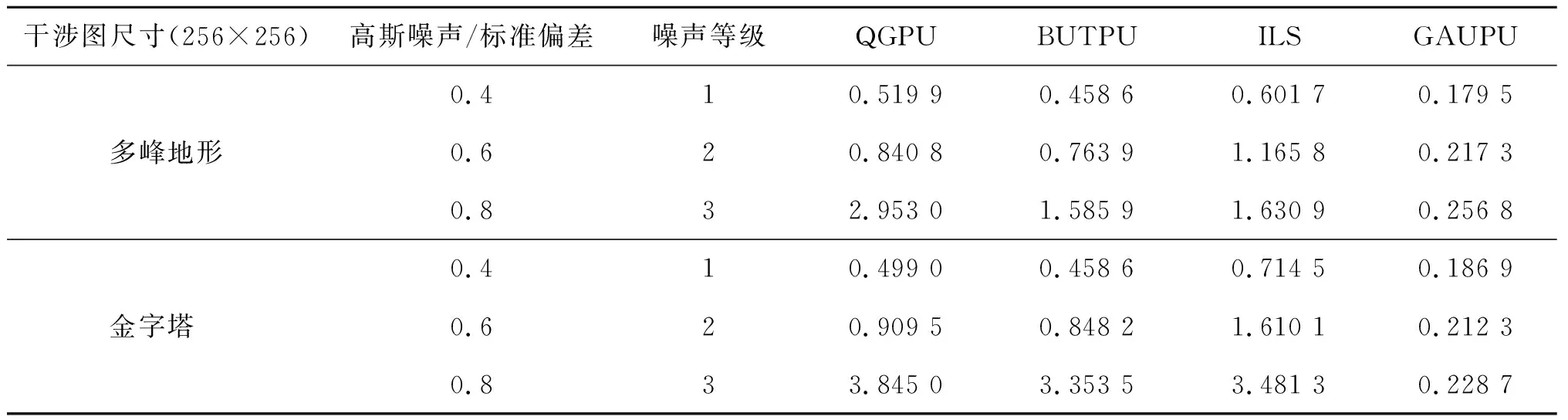
表2 不同噪声下的均方根误差对比

表3 各类算法运行时间 s

图5 不同相位解缠方法对图4(c)解缠结果

图6 不同相位解缠方法对图4(d)解缠结果

2.2 实测干涉图相位解缠实验

实测干涉图如图7所示,其中图7(a)为2021年5月21日21时48分在云南大理州漾濞县Sentinel1A卫星采集的局部云南干涉图,图7(b)为Rahul 干涉图[22]。

图7 实测干涉图

表4为图7(a)、图7(b)所示干涉图的噪声等级,图8、图9为QGPU、BUTPU、ILS、GAUPU方法分别对图7(a)、图7(b)解缠结果,其中图8、图9每行分别为QGPU、BUTPU、ILS、GAUPU方法解缠相位及对应的重缠绕图。从图9第1列,可观察到QGPU方法解缠相位图中存在明显相位不连续区域,尽管其解缠相位重缠绕图与实测干涉图条纹大致一致,但其仍存在大量噪声,易造成噪声误差沿质量引导路径蔓延,易导致相位解缠精度下降或其解缠结果不可靠。从图9第2列可看出,BUTPU方法解缠相位在残差点分布较为密集的地方形成了大量无法解缠的封闭区域,造成了孤岛现象的产生,导致解缠失败。图8第3列中ILS方法所得到的解缠相位较为平滑连续,但解缠相位重缠绕图与实测干涉图相比存在明显不一致条纹,造成条纹细节信息的丢失,导致其解缠相位可靠性降低。与上述3类算法相比,本文算法解缠相位连续光滑,其解缠相位重缠绕图条纹与实测干涉图条纹基本一致,且在重缠绕图中几乎没有噪声,表明该算法有效抑制噪声影响的同时具有较好的解缠结果。

表4 实测干涉图噪声等级

图8 不同解缠方法对图7(a)解缠结果

图9 不同解缠方法对图7(b)解缠结果

3 结束语

GAUPU算法把注意力上采样GAU和PU-M-Net结合起来,通过构建缠绕相位与真实相位之间的映射关系来实现干涉图解缠,完成训练后的网络可解缠不同噪声量级的干涉图。模拟干涉图与实测干涉图相位解缠实验证明了本文算法的有效性,且与QGPU、BUTPU、ILS等传统算法相比,在获得较为稳健的相位解缠结果的同时,其时间消耗亦远小于上述两种算法。