计及需求侧响应的蜂巢状有源配电网优化调度方法
2023-09-02王胜昔
王胜昔
(国网湖北省电力有限公司恩施市供电公司,湖北 恩施 445000)
0 引 言
蜂巢状有源配电网发电安排通常需要根据电网负荷的变化作出实时调整和改变,即需要根据实际情况作出合理的优化调度,以此消除运行负荷,保证蜂巢状有源配电网的稳定和安全运行。然而,与普通配电网相比,蜂巢状有源配电网内部结构更加复杂,对需求侧响应的依赖性更高,因此其优化调度具有一定难度。
然而,目前的调度方法未充分考虑蜂巢状有源配电网的需求侧响应,导致在实际应用中难以达到预期的效果,不仅使蜂巢状有源配电网出现负荷率偏低的情况,还增加了线路容量越限率。针对该问题,提出计及需求侧响应的蜂巢状有源配电网优化调度方法。
1 用户需求预测
蜂巢状有源配电网优化调度前,需要预测用户需求和综合用电成本[1]。用户综合用电成本主要包括用户负荷转移成本、用户购电费用、用户配电线路损耗成本3 部分。蜂巢状有源配电网中的有源电力电子设备可以控制电能流动和电压大小,有效降低线损,因此暂不考虑用户配电线路损耗成本,仅针对用户负荷转移成本和用户购电费用2 部分展开分析。
假设蜂巢状有源配电网在i时刻到j时刻的总转移负荷为P,则用户负荷转移成本计算公式为
式中:Fu(i-j)表示蜂巢状有源配电网在i时刻到j时刻的电量总转移成本;FP表示i时刻到j时刻的总转移负荷成本;Fg表示i时刻到j时刻时间间隔的电量转移成本;Fa(i-j)表示蜂巢状有源配电网在i时刻到j时刻与转移电量有关的成本;e表示变动成本系数;m表示固定成本系数;Fq(i-j)表示蜂巢状有源配电网在i时刻到j时刻与时间间隔有关的成本[2]。
电力用户购电费用包括用户响应分时电价前的购电总费用和响应分时电价后的购电总费用。假设未参与分时电价时的购电价格为k,则用户响应分时电价前购电总费用的计算公式为
式中:Ca表示用户响应分时电价前的购电总费用;G表示未参与分时电价时的购电量[3]。
假设蜂巢状有源配电网“峰、平、谷”3 个时段的购电价格分别为b1、b2、b3,则用户响应分时电价后的购电总费用计算公式为
式中:Cb表示用户响应分时电价后的购电总费用;t表示用户响应分时电价的时间;T1、T2、T3分别表示蜂巢状有源配电网“峰、平、谷”的时间;W1、W2、W3分别表示蜂巢状有源配电网“峰、平、谷”3 个时段的用户购电量[4]。
2 计及需求侧响应的目标函数建立
结合对用户需求的预测分析,以用户购电费用最小、用户满足度最大、蜂巢状有源配电网运行成本最小为目标,建立目标函数。其中,用户购电费用最小目标函数的公式为
式中:f1表示用户购电费用最小值[5]。
用户满意度主要与蜂巢状有源配电网负荷量有关,用户满意度最大目标函数公式为
式中:f2表示用户满意度最大值;D表示蜂巢状有源配电网中断负荷量;K表示蜂巢状有源配电网重要负荷量;S表示蜂巢状有源配电网最大可中断负荷量。
综合考虑中断负荷补偿成本和可平移负荷补偿成本等需求侧管理费用,建立蜂巢状有源配电网运行费用最小目标函数,其公式为
式中:f3表示蜂巢状有源配电网运行费用最小值;N表示蜂巢状有源配电网可控机组台数;t表示电网调度时段;Jsd.t和Psg.t分别表示蜂巢状有源配电网可控机组在调度时间段t的单位发电成本系数与有功功率;Jed.t和Peg.t分别表示蜂巢状有源配电网风机的运行维护成本系数与有功功率;Jer.t和Per.t分别表示蜂巢状有源配电网光伏列阵的运行维护成本系数与有功功率;Jrt.t和Prt.t分别表示蜂巢状有源配电网储能装置的运行维护成本系数与有功功率。
将式(4)~式(6)3 个目标函数整合为一个综合目标函数,其公式为
式中:f表示蜂巢状有源配电网优化调度目标函数。
3 设定约束条件
结合式(4)~式(7),根据配电网运行特征和需求,约束电网优化调度,对配电网负荷转移时段的约束条件公式为
式中:φ1表示约束条件1;tyu表示配电网负荷转入时刻;Tyt表示配电网负荷响应周期;tuy表示配电网负荷转出时刻。
分时电价实施后,考虑用户电能消耗会受到约束,其约束条件公式为
式中:φ2表示约束条件2;μrt表示配电网负荷转移前用户用电量;μtu表示配电网负荷转移后用户用电量。
4 蜂巢状有源配电网最优调度策略生成
以约束条件为依据,利用粒子群算法求解目标函数,根据配电网实际情况设定粒子群算法参数,包括粒子群数量和迭代次数等。假设每一个目标函数解为一个粒子个体,粒子群体通过迭代交叉操作,更新粒子位置,交叉操作后的粒子群得出的计算公式为。
式中:N表示蜂窝结构中交叉后的粒子数;S表示蜂窝交叉操作后的边长。
对变异操作后的粒子生成新的群体,再利用适应度函数计算出新的群体中粒子的适应度值,按照适应度值大小对粒子进行排序,输出适应度值最大的粒子,该粒子对应的解就是最优调度策略。执行该最优调度策略,从而实现计及需求侧响应的蜂巢状有源配电网优化调度。
5 实验论证
5.1 实验准备与设计
实验中,将蜂巢状有源配电网优化起始时间设定为10:00,结束时间为次日10:00。
在应用本文方法进行优化调度前,需要先对粒子群算法的参数进行如下设定:粒子种群数量为100,粒子种群迭代次数为200,粒子权重设定为0.45,学习因子设定为0.1。在求解目标函数的基础上,执行优化策略。
为使实验结果与实验数据更具说明性,选择2种传统方法作为对比,分别对蜂巢状有源配电网实施优化调度。2 种传统方法分别为基于消费者心理的调度方法和基于供需互动的调度方法,分别用传统方法A 与传统方法B 表示。
5.2 实验结果与讨论
实验首先以蜂巢状有源配电网负荷率为评价指标,验证3 种方法的应用效果。通常配电网负荷率的最佳范围在80%~90%,此时既能保证电网安全又能提高电力生产效益。实验以调度时间为变量,使用电子表格记录调度时间内各个时间点配电网负荷率的数值,根据记录结果,应用不同方法后配电网负荷率对比如图1 所示。
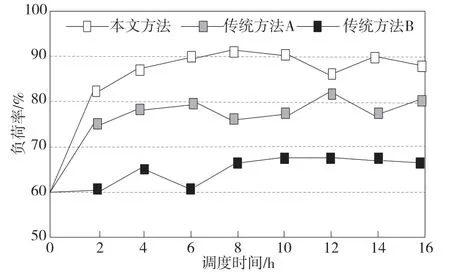
图1 应用不同方法后配电网负荷率对比
分析图1 可以看出,在应用本文方法后,蜂巢状有源配电网的负荷率基本保持在80%~90%,变化较为稳定。而应用2 种传统方法后,配电网的负荷率始终低于应用本文方法的负荷率,且应用传统方法B 后,配电网的负荷率甚至低于70%。由此可以说明,本文方法可以有效优化配电网负荷率,在保证配电网安全的同时,有效提高电力生产效益。
为进一步验证设计方法的适用性,对比分别应用3 种方法的蜂巢状有源配电网线路容量越限率。线路容量越限率可以反映配电网优化调度的合理性,线路容量越限率越低,配电网优化调度越合理。实验以配电网优化调度周期为变量,使用电子表格记录不同调度周期下蜂巢状有源配电网线路容量越限率,应用不同方法后配电网线路容量越限率对比的具体数据如表1 所示。

表1 应用不同方法后配电网线路容量越限率对比
由表2 中的数据可知:应用3 种方法后,蜂巢状有源配电网线路容量越限率均呈现出不断增加的态势;在应用本文方法后,线路容量越限率相对较低,线路容量越限率保持在0.02%~0.38%;而应用传统方法A 和传统方法B 后,线路容量越限率的最大值分别达到了25.11%和28.11%,明显高于本文方法。
6 结 论
此次从需求侧响应角度出发,设计了一套新的蜂巢状有源配电网优化调度方案,有效降低了蜂巢状有源配电网负荷和蜂巢状有源配电网线路容量越限率,实现了对现有配电网优化调度理论的补充与完善以及对传统方法的优化与创新,为计及需求侧响应的蜂巢状有源配电网优化调度提供了参考依据,具有一定的研究价值。但是,本文设计方法尚未在实际中得到大量的实践与应用,在某些方面可能存在一些不足之处,今后会在方法优化设计方面展开进一步研究,为蜂巢状有源配电网优化调度提供有力的理论支撑。
