理解概念本质 构建数学模型——《路程，时间和速度》教学实录

文|项荣花 孙 慧

【教学内容】

人教版四年级上册第53 页。

【教学过程】

一、回忆生活，唤醒经验

师：大家在生活中遇到过比快慢的情况吗？你们是怎样比的？

生：跑步比赛，先到终点的人跑得快。

生：1 分钟口算，谁算对的题目多，谁快。

二、结合情境，初建模型

师：四（1）班组织游学活动，想预约一辆开得快一些的车。你有办法帮助他们吗？

根据学生建议，课件依次演示：

两辆汽车在同一起点出发，看哪一辆率先到达终点。

小结：路程相同，比时间，时间越短，车开得越快。

两辆汽车同时出发，半小时后，看谁行得较远。

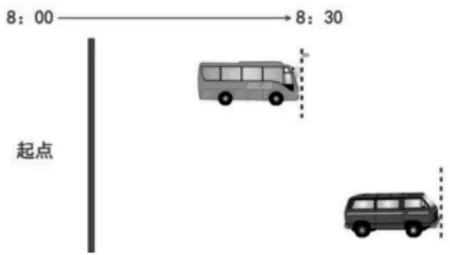
小结：时间相同，比路程，行驶的路程越长，车开得越快。

师：但是旅游公司不打算让这两辆车特意比赛一场，他们提供了一份过去的行驶记录。

车型时间路程大巴车6:30～9:30150 千米中巴车8:00～10:00120 千米

师：你能从表中得到哪些数学信息？根据这些信息能判断哪辆车开得快吗？

生：我看到大巴车3 小时行驶了150 千米。中巴车2 小时行驶了120 千米。

生：大巴车开的时间长，行得也远。

生：行的时间和路程都不一样，要算一算才能知道快慢。

师：好的，那大家算一算，把自己的想法记录在《学习单》上。

师：老师这里收到一个方案，大家看看，觉得怎么样？

方法一：

生：这位同学的想法和我一样，中巴车2 小时行120 千米。照这样计算，乘以3，中巴车6 小时可以行360 千米；同样道理，大巴车3 小时行150 千米，乘以2，6小时行300 千米。大家都行6 小时，中巴车行驶的路程多，所以中巴车行得快。

师：这位同学将题目转化成——时间相同比路程。

师：那我们可以把路程变得相同吗？

方法二：

生：我们可以假设路程都是600 千米，600÷150=4（个），600 千米里面有4 个150 千米，需要4个3 小时，也就是大巴车行600千米需要12 小时；同样道理，600÷120=5（个），2×5=10（小时），中巴车行600 千米只要10 小时。中巴车行得快。

师：还有不同的想法吗？

生：我不需要转化，可以直接计算。

师：能看懂他的方法吗？

生：他是用路程÷时间。

生：我知道路程÷时间的结果叫“速度”。

生：大巴车3 小时行150 千米，150÷3=50，大巴车每小时行50千米；120÷2 就是中巴车每小时行60 千米。这样也可以比出中巴车开得更快一些。

根据学生回答，边演示课件线段图，边引导分析：

师：已知条件是大巴车3 小时行150 千米，中巴车2 小时行120 千米——

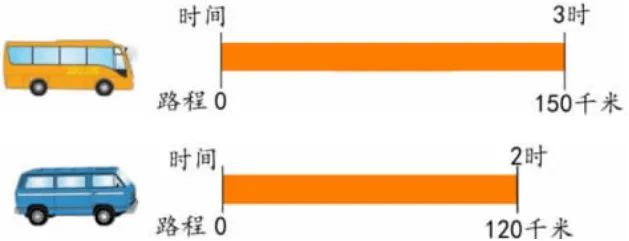
师：我们可以把150 千米按3小时平均分，把120 千米按2 小时平均分——

师：大巴车的情况，平均每小时对应的路程是——50 千米，平均每时行50 千米，2 小时行100千米，3 小时行150 千米。

师：“中巴车的情况——”谁能像老师这样说一说？

生：按2 小时平均分成2 份，平均每小时行60 千米，2 小时行120 千米。

师：说得真好。我们把时间和路程同步平均分，求出了车的——“速度”！能说说你现在对速度的理解吗？

生：速度就是路程÷时间算出来的。

生：我们把路程和时间对应地平均分，分出来看每小时行多少路程就是速度是多少。

小结：像这样，根据已知的时间和路程，算出平均每小时行驶多少千米，就是我们经常说的“速度”。（板书：路程÷时间=速度）

三、细化模型，深化理解

师：同学们真了不起，在时间和路程都不同的情况下，创造了计算“速度”来比快慢的方法。“速度”就是一个专门用来刻画快慢的数学概念。试着在练习纸上算一算我们身边常见的速度。

（学生自主作业，集体反馈）

师：和他一样的同学请举手。不算不知道，原来他们的速度都是8 米，他们都一样快啊！

生：老师，尽管他们的速度都是8 米，但他们的速度不一样。

生：孙老师的8 米是平均每秒跑8 米；蜗牛的8 米是平均每时爬8 米；海龟是平均每分爬了8米。都是8 米，但用的时间不一样。

师：有什么办法“改造”一下？让别人一眼就能看出他们的速度是不一样的。

生：我们都按照1 小时来算。蜗牛1 小时行8 米，孙老师每秒跑8 米，就是1 分钟跑480 米，就是1 小时跑……

生：我还有一个想法，把孙老师的速度算成每小时的话，我觉得不太合理，因为孙老师短时间可以跑到这个速度，长时间可能会越跑越慢。

生：我觉得可以在答案后面添省略号。8 米……每秒；8 米……每时；8 米……每分。

师：你们怎么看？这样写能表达出各自的速度信息吗？看得出谁快谁慢吗？

强调：速度里面包含着两个信息，一个是路程，一个是时间，我们看速度，要兼顾时间和路程。所以，在数学上，速度单位可以这样写：8 米/秒、8 米/时、8 米/分。

师：（指8 米/秒）这个读作8米每秒，表示平均每秒跑了8 米。

师：第二个、第三个谁来读一读、说一说？

生：8 米/时读作8 米每时，表示平均每时爬了8 米。

生：8 米/分读作8 米每分，表示平均每分爬了8 米。

师：解决了这个问题，你对速度有什么新的认识吗？

生：路程÷时间=速度，速度不是简单的一个数，这个数里面既有路程又有时间。

生：速度的单位和我们以前学的应用题里的单位不一样，既要显示路程，又要显示时间。

小结：平均每时、每分、每秒行驶的路程，也就是“单位时间”所行“路程”的情况，称作“速度”。“速度”这个数量不简单，它表示着路程和时间之间的关系，所以它的单位是：长度单位/时间单位。

四、融入生活，感受速度

师：我们知道了人、蜗牛和海龟的行进速度，你们还知道其他事物的速度信息吗？

生：我们家里的网速现在可以达到18 兆/秒。

生：水从食道到胃速度大约是6～8 厘米/秒。喝一口水，5 秒钟就可以到胃部。

师：大家真是见多识广呀。老师也收集了一些信息。

师：看了这些数据，你有什么想说的吗？

生：高铁运行的最高速度大约为350 千米/时，表示高铁平均每小时行驶350 千米。那从上海到丽水，大约需要2 个半小时。上海到龙泉的铁路距离有875 千米。

生：高铁运行的最高速度是350 千米/时，一般不会达到这个最高速度。我坐高铁的时候看到电子屏上经常显示的是200 千米/时、180 千米/时。

生：飞机飞行的速度大约是12千米/分，那也就是720 千米/时，飞机的速度大约是高铁的2 倍。

生：光传播的速度大约为30万千米/秒，声音的传播速度大约为340 米/秒。光速比音速快很多，所以我们先看到闪电，再听到雷声。

生：唾沫传播的最快速度大约是50 米/秒，表示唾沫平均每秒就能传播50 米。一眨眼的功夫，唾沫就横穿了5、6 个教室。

五、自主作业，反思拓展

1.布置书面作业，学生独立完成，教师巡回批改。

（1）兔子和乌龟哪个速度快？他们的速度分别是多少？

兔子3 分钟跑了240 米；乌龟2 小时爬了160 米。

（2）这段路总长180 千米，老师想用2 小时开完这一段路。会超速吗？

2.集体反馈。

师：第（1）题大家做得都很好，我们重点看看第（2）题。图中的“60”是什么意思？

生：速度不能超过60 千米/时。

生：最快只能开到60 千米/时。

师：老师收集到三份方案，你们看看，能看懂这几位同学分别是怎么想的吗？

生：第一种，是比速度。2 小时行完180 千米，意味着速度要达到90 千米/时，超过了60 千米/时。

师：他的速度是怎么计算的？

生：路程÷时间=速度。

生：我是第二种，比路程。按60 千米/时的速度，2 小时最多只能行使120 千米，实际路程有180千米，不超速不能走完。

师：你们的路程是怎样算出来的？

生：路程=速度×时间。

（板书：速度×时间=路程）

生：第三种，比时间。180÷60=3（时），正常需要3 小时行完。只有超速才能2 小时行完。

师：时间又可以怎么计算？

生：路程÷速度=时间。

（板书：路程÷速度=时间）

小结：路程、时间、速度三个量，只要知道其中两个量，就可以求出第三个量。同一个问题，可以从不同角度，计算不同的数量，进行比较、解决。

六、全课总结

师：通过今天的学习，你有什么收获？

生：通过今天的学习，我知道了路程÷时间=速度，算出速度的大小，可以代表行车的快慢。

生：路程、时间与速度三个量，我们只要知道其中的两个量，就能求出第三个量。

生：速度很特别，一个数里藏着两个数量，既有路程又有时间，它的单位是双重的。

生：光速、网速、飞沫传播的速度都很快。