Rough Heston Models with Variable Vol-of-Vol and Option Pricing

Hui Liang ,Jingtang Ma and Zhengguang Shi

1 School of Science,Harbin Institute of Technology,Shenzhen,Guangdong 518055,China

2 School of Mathematics,Southwestern University of Finance and Economics,Chengdu,Sichuan 611130,China

3 School of Mathematical Sciences,Sichuan Normal University,Chengdu,Sichuan 610066,China

Abstract. In this paper,a rough Heston model with variable volatility of volatility (vol-of-vol) is derived by modifying the generalized nonlinear Hawkes process and extending the scaling techniques.Then the nonlinear fractional Riccati equation for the characteristic function of the asset log-price is derived.The existence,uniqueness and regularity of the solution to the nonlinear fractional Riccati equation are proved and the equation is solved by the Adams methods.Finally the Fourier-cosine methods are combined with the Adams methods to price the options.

Key words:Rough Heston model,option pricing,Hawkes process,fractional differential equations,Fourier-cosine methods.

1 Introduction

The classical Heston model invented by Heston [27] has been received large popularity in the financial market due to that it generates very reasonable shapes of the implied volatility surface and there is analytic formula for the characteristic function of the asset log-price.In a recent paper by Gatheral,Jaisson and Rosenbaum [24],it is empirically shown that the financial time series of the realized volatility exhibit much rougher than that of the Brownian motion for the volatility in the classical Heston model.The dynamics of the log-volatility behave essentially as a fractional Brownian motion with Hurst parameterHless than 1/2.Therefore,many researchers have focused their studies on fractional Brownian motion and use it to express the squared volatility process in the financial models.The fractional Brownian motion can be expressed by the Mandelbrot-Van Ness representation(see e.g.,[40]) which contains an integral process.Since the integral process has H¨older regularityH−∊for any∊>0,in the rough Heston model,the kernel of the form (t−s)H−1/2is often introduced in the squared volatility process.For example,in [17] it gives a rough Heston model on a filtered probability space(Ω,F,F,P) of the form

where the parametersγ,θ,ν,V0,S0are positive constants,α:=H+1/2∈(1/2,1),andWandBare two Brownian motions with correlation coefficientρ ∈[−1,1].Ifα=1,then the rough Heston model (1.1a)-(1.1b) coincides with the classical Heston model.Therefore,the rough volatility model (1.1a)-(1.1b) can be viewed as the rough extension of the classical Heston model.However,the rough squared volatility model (1.1b) is not Markovian and the variance process is not anymore a semi-martingale.Therefore,the use of the Monte-Carlo methods for the option pricing under the rough Heston model becomes quite intricate (see [9]) and the analytic method in [27] is also hard to adapt to the rough Heston model.

Jaisson and Rosenbaum[31]investigate the nearly unstable Hawkes process and show that it asymptotically behaves like an integrated Cox-Ingersoll-Ross model(see [11]),i.e.,the squared volatility process of the classical Heston model.The Hawkes process is a kind of self-exciting and mutually exciting point processes introduced by[28,29].The essential property of Hawkes process is that the occurrence of any event increases the probability of further events occurring.Over that last decades,the probabilistic and statistical analysis of Hawkes processes has known several interesting developments,driven by the growing use of Hawkes processes in finance,see e.g.,[1,2,4–7,10,14,15,37],and the recent review paper by [30] and the reference therein.

Based on the framework by Jaisson and Rosenbaum [31],Jaisson and Rosenbaum [32] investigate the asymptotic behavior as time goes to infinity of Hawkes process whose regression kernel hasL1norm close to one and power law tail of the formt−(1+α),withα∈(0,1)and prove that whenα∈(1/2,1),after properly re-scaling,the law of a nearly unstable heavy tailed Hawkes process converges to a fractional version of the Cox-Ingersoll-Ross model,i.e.,squared volatility process of the rough Heston model.Enlightened by Jaisson and Rosenbaum[32],El Euch,Fukasawa and Rosenbaum [18] bridge the connection between market microstructure and rough volatility by proposing a microscopic price model and by indicating that it converges to a rough Heston setting in the long term and show that typical behaviors of market participants at the high frequency scale generate leverage effect by means of the properties of nearly unstable heavy tailed Hawkes process.Considering its paramount to the practice when models have a nonzero initial volatility,El Euch and Rosenbaum [17] resort modified sequence of Hawkes-type processes to obtain a non-degenerate initial rough volatility and derive the characteristic function of the asset log-price.It is worth noting that the other definitions of rough Heston model maybe make sense,see in [26] for an alternative definition and some asymptotic results.

El Euch and Rosenbaum [19] provide that the mean-reversion levelθin (1.1b)is replaced by a time-dependent one in order to be consistent with the market forward variance curve,and lead to perfect hedging.Jaber and El Euch [33] resort to a sequence of exponentially decaying kernels approximated the fractional kernel (t−s)α−1in (1.1b),yielding a sequence of conventional multi-factor stochastic volatility models that is shown to converge to the rough Heston model in a specified region.Inspired by the approximation results of Jaber and El Euch [33],Jaber [35]provides a good parametrization of the multi-factor parameters in terms of one single Hurst parameterH,which is nothing else but the Hurst index of a limiting rough Heston model,obtained after sending the numbers of factors to infinity.Jaber and El Euch[34]study the Markovian and affine structure of (1.1b)in terms of an infinitedimensional adjusted forward process and specify its state space.More precisely,they show that it satisfies a stochastic partial differential equation and displays an exponentially-affine characteristic functional.Gatheral and Keller-Ressel [25] introduce a class of affine forward variance models of which the rough Heston model is a special case and show that the affine forward variance models can be characterized by the affine form of their cumulant generating function,which can be obtained as solution of a convolution Riccati equation.

As shown by the empirical studies the prices from the stochastic volatility model with constant vol-of-vol are not supported by market prices.As a result financial engineers have to recalibrate model parameters every day to new market data.For this reason,Benhamou,Gobet and Miri[8],Forde and Jacquier[21]construct timedependent vol-of-vol to make it consistent with a pre-specified term structure for the variance of the integrated variance.Nevertheless,to the extent of our knowledge,published papers on rough Heston model with variable vol-of-vol,namelyνis(1.1b)that is not a constant but a function of time,are very rare.Hence,stimulated by [17,18,32],and with suitable modification of the generalized nonlinear Hawkes process,we derive the rough Heston model with variable vol-of-vol as follows:

where the parameterδis a positive constant andσ(s)a given differentiable function,and the remaining parameters are as the same as that in(1.1a)-(1.1b).Without the kernel(t−s)α−1,the above processes become the time-inhomogeneous affine diffusion in [23].Analogously to [36] for deriving the characteristic function using the timehomogeneous affine processes of [13],we deduce the characteristic function of the log-price in rough Heston model with variable vol-of-vol (1.2a)-(1.2b),i.e.,

whereh(t) is a solution of the following fractional Riccati equation:

with initial conditionI1−αh(0)=0,where the fractional integral operatorI1−αand fractional differential operatorDαare given by(3.9)in the next section,respectively.Thirdly,we prove the existence and uniqueness of the solution to the nonlinear fractional Riccati equation (1.3) by Picard iteration,and study its regularity.Since there is no closed-form solution to the nonlinear Riccati equation (1.3),numerical methods need to be developed to solve the equation.Therefore the studies on the existence,uniqueness and regularity of the solution to the nonlinear fractional Riccati equation (1.3) play an important role to ensure the accuracy of a numerical scheme for solving it.We use the predictor-corrector schemes in line with Adams method(see[12])to compute the fractional nonlinear Riccati equation(1.3).Adapting with the predictor-corrector schemes,we use the Fourier-cosine methods (see [20] in details) to price the European option under the rough Heston models with variable vol-of-vol (1.2a)-(1.2b).

The rest of the paper is organized as follows.In Section 2,we modify the nearly unstable heavy tailed Hawkes processes and give preliminary results.In Section 3,we build a sequence of Hawkes-type processes and prove that it converges to the rough Heston model with variable vol-of-vol (1.2b).Moreover,we derive the nonlinear fractional Riccati equation for the characteristic function of the asset log-price.In Section 4,we give the existence,uniqueness and regularity of the solution to the nonlinear fractional Riccati equation (1.3),propose the numerical schemes to solve it,and use the Fourier-cosine methods to compute the option prices.Numerical examples are given in Section 5 and conclusions in Section 6.

2 Generalization of Hawkes process and preliminary results

The Mittag-Leffler functionEζ,ηis defined by

Forα∈(1/2,1) andγ∈R+,we also define

We can get the following properties offα,γandFα,γ(see [16,41] and references therein)

and

Using (2.2),we derive that

Define

whereϕT:=(1−γT −α)fα,1andβ≥0.

Definition 2.1.Consider {Nt≥0} a counting process,with associated history {Ht:t≥0},that satisfies

where the components satisfy(2.4)and suppose the process conditional intensity function is of the form

with µ,ξ,γ>0,α∈(1/2,1),T >1/γ−1/α and σ(t)is a given differentiable function on[0,1].This is called generalized nonlinear nearly unstable heavy tail Hawkes process.

Using (2.3),we derive that

From (2.4),we get that

Let

where

Using methods of induction,we derive that

Lemma 2.1.We have the following identity

where fα,γ and ψT are defined by(2.1)and(2.8),respectively.

Proof.Forα∈(1/2,1),fα,γ(t)is square-integrable and its Laplace transform is given by,forz>0,

Using (2.8) and methods of induction,we derive that

where

Consequently,

Using the Laplace inversion to both sides of identity (2.10)completes the proof.

3 Rough Heston model with variable vol-of-vol

Define the re-normalized Hawkes process

and its associated integrated intensity

We also introduce the compensated process

The proofs of Lemmas 3.1 and 3.2 are analogous to that in [17] for the convergence of a microscopic price model to a rough Heston models with constant vol-of-vol and the main difference is that the vol-of-vol is time-dependent.

Proof.Using(2.5)and(2.9)together with stochastic Fubini’s theorem[44,Theorem 2.2],and

we get

Therefore it follows from (2.7) that

The remaining of the proof follows [17] in a straightforward manner.

where(B1,B2)is a bi-dimensional Brownian motion and Yt is the unique solution of

where β≥0,µ,ξ,γ and σ(t)are given by(2.6b),and

Proof.The proof is given by Appendix A.

Now we build up the microscopic connection of the stock log-price process with the Hawkes process and derive the rough Heston model with variable vol-of-vol.To this end,we define

Then we derive the following rough Heston model with variable vol-of-vol.

Theorem 3.1.The rough Heston model with variable vol-of-vol is given by

where

W and B are two Brownian motions with correlation coefficient

Then the proof is completed.

Jaber,Larsson and Pulido [36] derive the characteristic function for a class of time-independent affine Volterra processes,that is,vol-of-volσis a constant and they provide explicit exponential-affine representations of the Fourier-Laplace functional in terms of the solution of an associated system of deterministic integral equations.In this section,we extend the results to the time-dependent affine processes,that is,we consider the vol-of-volσis not a constant but a function of timeσ=σ(t).We derive that the characteristic function for the affine Volterra process (3.6) is expressed by the solution of a nonlinear fractional Riccati equation.

Theorem 3.2.For the affine Volterra process(3.6)and fix some T<∞,u∈Cand h∈L2([0,T],C).The characteristic function of(3.6)is

where S and V represent the values of stock and volatility at t=0,respectively,and h(t)satisfies a fractional Riccati equation

where I1−α and Dα are fractional Riemann-Liouville integral operator and derivative operator,which are defined respectively by

Proof.The proof is given by Appendix B.

4 Solution of the nonlinear fractional Riccati equation and the option pricing

The fractional Riccati equation(3.8)can be written as the following Volterra integral equation

where

Theorem 4.1.Let Q>0,define the set

and suppose that the function L:Ω→Ris continuous and bounded inΩand that it fulfils a Lipschitz condition with respect to the second variable,i.e.,there exists a constant A>0such that,for all(t,y1)and(t,y2)∈Ω,we have

Then the integral equation(4.1)has a unique solution h∈C[0,δ0],where

Proof.The proof can be obtained using the following Picard iteration

withh0(t):=0.Since the derivation is very standard (see,e.g.,[3],we omit the details).

Theorem 4.2.Assume that the given functions in the(4.1)satisfy

Then Dαh(t)∈C2(0,T],1/2<α<1,where Dα is defined by(3.9).

Proof.We first use the methods of induction to prove that the solutions of Picard iteration (4.2) are

where

and forn≥1

Forn=0,using (4.2),we have

Assume that (4.3) is true for alln=1,2,···,k.Then we need to prove that (4.3)holds true also forn=k+1.Substituting (4.3) into (4.2),we can get

Using the fact that the third term on the right-hand side of (4.5) can be written as

Hence,we derive that

Applying fractional differential operatorDαto the both sides of (4.7),we have

which gives thatDαh(t)∈C2(0,T],1/2<α<1.

Now we use the two-step fractional Adams scheme on graded meshes to solve the Volterra integral equation (4.1).Define graded meshes on [0,T] as

On the graded meshes,we estimate

where

It then leads to

where

Moreover using product rectangle rules,we derive that

where

Combining (4.8) and (4.10),we give the two-step fractional Adams scheme,which is an explicit scheme,as

We now present the convergence rates of the scheme (4.11).

Theorem 4.3.Under the same condition as Theorem4.2,the error of the two-step fractional Adams scheme(4.11)for solving(4.1)is estimated by

Proof.This is just a corollary of [38,Theorem 1.5].

Now we derive the numerical formula for the characteristic function(3.7).Using the Richardson extrapolation technique of trapezoidal formula and scheme (4.11)for approximatingh,we derive that

whereKis strike price,Nis an even number,

and

The Fourier-cosine methods in [20] (see appendix for the details) are very efficient to compute the option price under the condition that the characteristic functions can be fast computed.Since the characteristic functions Θ can be calculated byin (4.12),the Fourier-cosine methods are the good choices to compute the prices of options under the rough Heston model with variable vol-of-vol (3.6).

5 Numerical examples

In this section,we carry out two numerical examples to verify the convergence rates of the two-step fractional Adams scheme (4.11) for solving the Volterra integral equation (4.1) which is equivalent to the factional Riccati equation (3.8) and calculate the option prices under the time-dependent vol-of-vol Heston models.Since the exact solution of the problem is not known,we shall use the following formula

to calculate the convergence rates (see [39]).The codes for the examples are run in MATLAB R2017a on a PC with the configuration:Intel(R)Core(TM) i7-8550UCPU@1.80GHz 1.99GHz and 8.0GB RAM.

Example 5.1.The aim of this example is to verify the the two-step fractional Adams scheme(4.11)for solving the Volterra integral equation(4.1)and calculating the characteristic function (4.12).The values of parameters are given as follows.

(i) We use the calibrated parameters in [17]:

and the time horizon is taken asT=5.

(ii) We use the calibrated parameters in [33]:

and the time horizon is taken asT=1.

The complex numberuis taken asu=iand the graded mesh parameter is set byp=2.Moreover,the vol-and-vol functions are takenσ(t)=from [22] andσ(t)=0.2−0.05tfrom [21].

From Tables 1 and 2,we see that the convergence rate isN−(1+α),which agrees well with the convergence results in Theorem 4.3.

Example 5.2.In this example,under risk-neutral measure Q,we calculate the prices of the European put options for the rough Heston model,

where Et,S,Vis a conditional expectation operator given thatSt=S,Vt=V.The strike priceK=80,100,120,the initial stock priceS=100 and the other parameters are the same as Example 5.1.

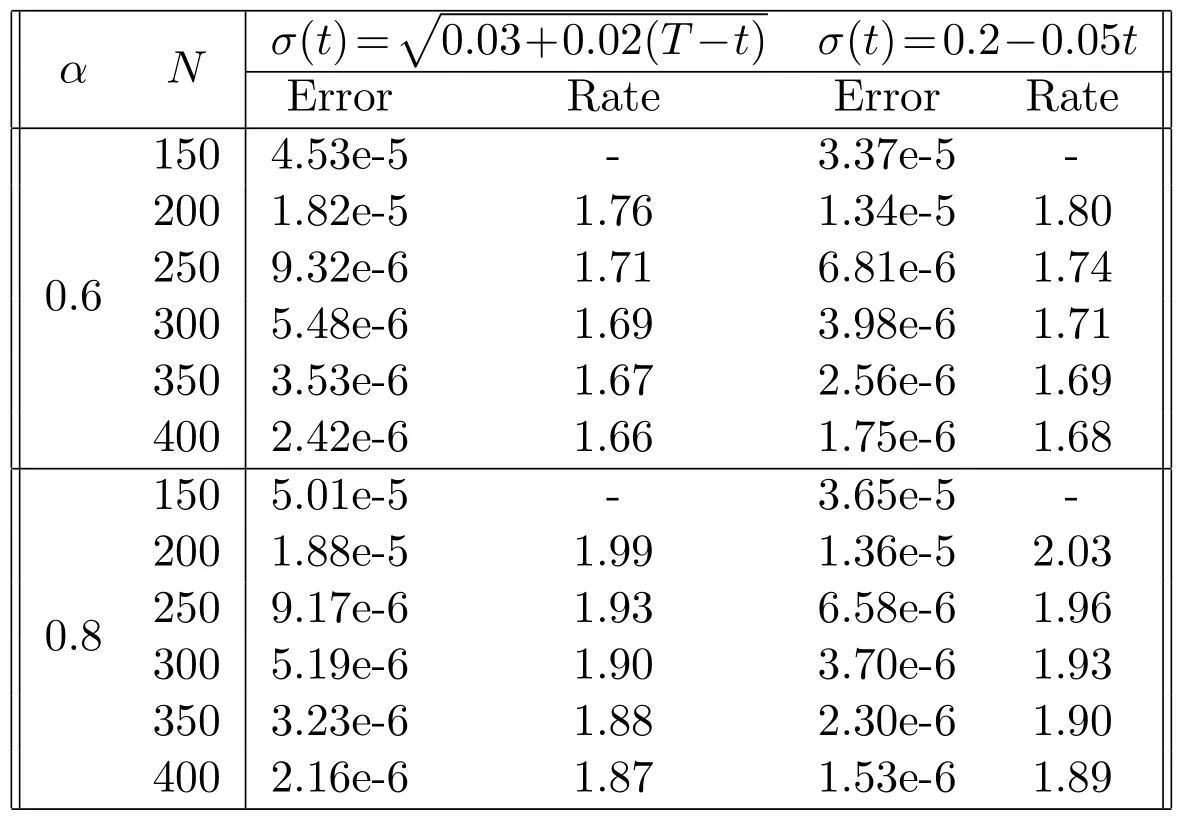
Table 1:Convergence rates of the two-step fractional Adams scheme (4.11) for Example 5.1 with the values of parameters in (i).

Letx:=ln(S/K) andy:=ln(ST/K).Then

Figure 1:The errors of Fourier-cosine methods for pricing European put options under the rough Heston model with σ(t)=,and the other parameters are the same as (i) of Example 5.1.We choose N=800, M=35,45,···,105 and the reference values are obtained by the Fourier-cosine method with N=1000 and M=115.

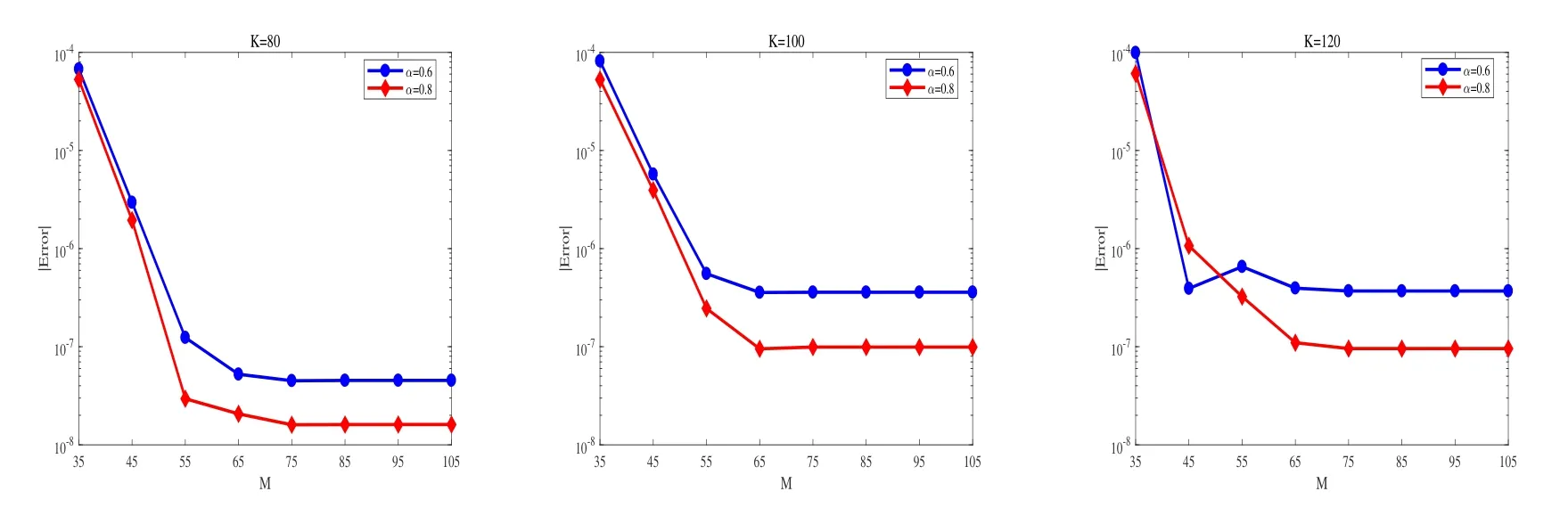
Figure 2:The errors of Fourier-cosine methods for pricing European put options under the Rough Heston model with σ(t)=,and the other parameters are the same as (ii) of Example 5.1.We choose N=800, M=35,45,···,105 and the reference values are obtained by the Fourier-cosine method with N=1000 and M=115.

and the Fourier-cosine method (see Appendix C) can be applied to compute the option prices.Tables 3 and 4 give the values of options,the computational time,the errors,and convergence rates of the computation.From the numerics in Tables 3 and 4,we see that the convergence rates with respect toNareN−(1+α)which are the same as the convergence results in Theorem 4.3 for the Adams schemes.As for the Fourier-cosine methods with respect to the number of Fourier nodesM,Figs.1 and 2 exhibit the exponential convergence rates.

Example 5.3.In this example,we calibrate the rough Heston model with variable vol-of-vol (3.6) using the real market data and compare it with constant vol-of-vol.To facilitate correction and optimization,we setδidentical toγin(3.6)and compare the performance of the rough Heston (RH),rough Heston with linear vol-of-vol(RHlv)and rough Heston with square root vol-of-vol(RHsv),which correspondingly,σ(t)=a,a+bt,,respectively.

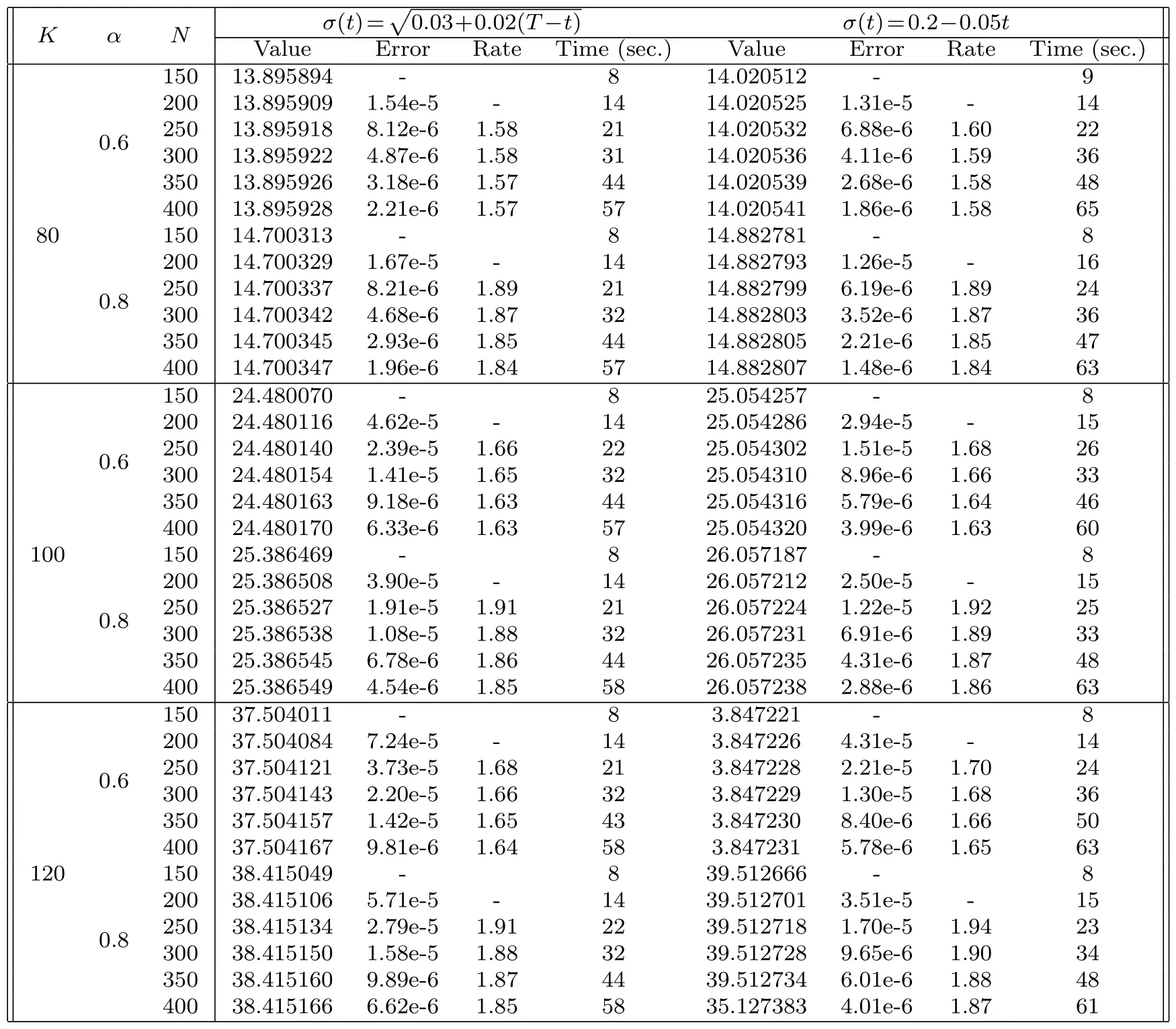
Table 3:Computational results for European put option pricing for Example 5.2.The number of Fourier nodes is taken as M=115 and the other parameters are the same as (i) of Example 5.1.

These models are calibrated on the S&P index option panel data on January 3,2017,which is composed of 306 S&P index options types of in-the-money,atthe-money and out-of-the money with the maturity containing 1 week,1 month,3 months,6 months,9 months,12 months,18 months,and 24 months.The calibration results are given as Table 5.

Table 4:Computational results for European put option pricing for Example 5.2.The number of Fourier nodes is taken as M=115,and the other parameters are the same as (ii) of Example 5.1.

whereNTrepresents the number of options at timeT.From Table 6,we see that error of the implied volatility for the rough Heston model with time-dependent volof-vol is smaller than the rough Heston model with constant vol-of-vol.

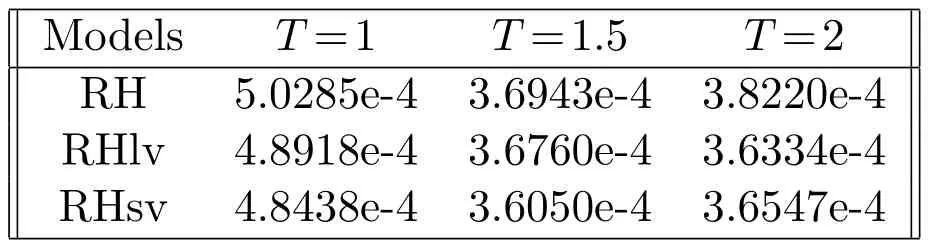
Table 6:Errors of the implied volatility.

6 Conclusions

In this paper,the time-dependent vol-of-vol rough Heston model is built by modifying the generalized nonlinear Hawkes process.The nonlinear fractional Riccati equation for the characteristic function of model is derived and the existence,uniqueness and regularities of the solutions are rigorously proved.The two-step fractional Adams scheme on graded meshes is used to solve the nonlinear fractional Riccati equation,and the European options are calculated by the Fourier-cosine methods.Numerical examples are provided to verify the efficiency and accuracy of the computations.

Appendix

A Proof of Lemma 3.2

Further using the Fubini’s theorem,we derive that

Therefore,recalling the definition (3.1),i.e.,

Noting that

From Lemma 3.1 we know that Λt=Xt.So substituting (A.2)and(A.3)into(A.1),we obtain that

with

By Lemma 3.1 and (A.4),we have

In the light of [42,Theorem IV-3.8],there exists a bi-dimensional Brownian motion(B1,B2) such that

Define a new Brownian motion

Then substituting (A.6) and (A.7) into (A.5),we obtain

Finally,by virtue of the technique in [18,Proposition 4.9],we derive that (A.8) is identical to (3.4).The proof is thus completed. □

B Proof of Theorem 3.2

andu,υ∈C.Write

with

and

for all 0≤t≤T.

Applying (B.1),the following identities are derived from (3.6),

Using (B.5b),Fubini’s theorem and then (B.1),we have

Moreover,we derive that

Substituting (B.7) and (B.8) into (B.6),we get

From (B.12) and (B.13),we obtain that

Then substituting (B.10) and (B.11) into (B.3) and using (B.13),(B.14) and the stochastic Fubini’s theorem,we obtain that

Since (B.1) can be re-written as [36,see Lemma 4.4]

Then using that exp(Y) is a martingale,we obtain that

We further taket=0 andυ=0 in (B.17),we obtain (3.7) and (3.8). □

C Fourier-cosine methods for option pricing

In this section,we briefly introduce the main idea of Fourier-cosine methods in [20]and use the method for computing the European option.

Following the main idea of Fourier-cosine method in [20],we explain how to derive the formula of European-style put options for rough Heston model.For an option pricing problem expressed in (5.1),define:=K(1−ey)+,we rewrite it into the following form

wheref(y|{x,V}) is the probability density ofygivenxandV.

Since the density rapidly decays to zero asy→±∞in (C.1),we truncate the infinite integration range without losing significant accuracy to[η1,η2]∈R,and obtain approximation

In the second step,sincef(y|{x,V}) is usually unknown whereas the characteristic function is,we replace the density by its cosine expansion iny,that is,

with

Due to the rapid decay rate of these coefficients,we further truncate the series summation of (C.3) to obtain approximation:

Suppose [η1,η2]∈R is chosen such that the truncated integral approximates the infinite counterpart very well,i.e.,

where Re{·}denotes taking the real part of the argument.ReplacingAk(x,V) in(C.4) byFk(x,V),we obtain

Finally,according to [20],we can choose the boundary of the integral as

where

andLis a positive constant which is a large enough to guaranteeη1<0<η2.

Acknowledgements

H.Liang was supported by National Natural Science Foundation of China(No.12171 122),Shenzhen Science and Technology Program (No.RCJC20210609103755110)and Fundamental Research Project of Shenzhen (No.JCYJ20190806143201649).J.Ma was supported by National Natural Science Foundation of China (Grant No.12071373).