An Arbitrary Order Reconstructed Discontinuous Approximation to Biharmonic Interface Problem

Yan Chen,Ruo Li and Qicheng Liu,

1 School of Mathematical Sciences,Peking University,Beijing 100871,China

2 CAPT,LMAM and School of Mathematical Sciences,Peking University,Beijing 100871,China

Abstract. We present an arbitrary order discontinuous Galerkin finite element method for solving the biharmonic interface problem on the unfitted mesh.The approximation space is constructed by a patch reconstruction process with at most one degrees of freedom per element.The discrete problem is based on the symmetric interior penalty method and the jump conditions are weakly imposed by the Nitsche’s technique.The C2-smooth interface is allowed to intersect elements in a very general fashion and the stability near the interface is naturally ensured by the patch reconstruction.We prove the optimal a priori error estimate under the energy norm and the L2 norm.Numerical results are provided to verify the theoretical analysis.

Key words:Biharmonic interface problem,patch reconstruction,discontinuous Galerkin method.

1 Introduction

We are concerned in this paper with the biharmonic interface problem.The biharmonic operator is a fourth-order elliptic operator which is frequently seen in the thin plate bending problem and the ions transport and distribution problem [19,33,40].Recently,there are many successful finite element methods proposed and applied to solve biharmonic problems,see e.g.,[7,11,17,25,35].The biharmonic interface problem arises in the context of composite materials where the physical domain is separated by an interface and the coefficient is discontinuous across this interface.Some efforts have been made to address this kind of problem [7,9,10,31,36].

The finite element methods for interface problems can be classified into two categories:body-fitted methods and unfitted methods.Body-fitted methods are constructed on a mesh aligned with the interface.This type of methods are naturally suited to deal with the discontinuity on the interface.However,generating a highquality body-fitted mesh can be a nontrivial and time-consuming task [29,32,37].In unfitted methods,the mesh is independent of the interface,and the interface can intersect elements in a very general way.As a result,unfitted methods have gained more attention for solving the interface problem.

In 2002,A.Hansbo and P.Hansbo proposed a Nitsche extended finite element method (XFEM) for solving the second-order elliptic interface problem.The idea of this method involves constructing two separated finite element spaces on both sides of the interface and using Nitsche’s types of penalty to weakly impose the jump conditions.Unfitted finite element methods based on this idea are sometimes referred to as cut finite element methods (CutFEMs).Since then,these methods have been further developed and applied to a range of interface problems,including Stokes interface problems,H(div)-and H(curl)-elliptic interface problems,elasticity interface problems,and so on.We refer to [6,14,15,18,20,24,32] and the references therein for recent advances.

For the biharmonic interface problem,Y.Cai and et al.proposed two Nitsche-XFEMs in [9] and [10].In [9],the authors used the so-called modified Morley finite element to approximate the solution near the interface and proved an optimal a priori error estimate under the energy norm.In [10],they derived a mixed method based on the Ciarlet–Raviart formulation with (P2,P2) finite element.Due to the high order of the biharmonic operator,it is hard to implement a high-order conforming space.Therefore,we aim to use the discontinuous Galerkin (DG) method to obtain the numerical solution to the biharmonic interface problem.

In this paper,we propose an arbitrary order discontinuous Galerkin CutFEM for solving the biharmonic problem with aC2-smooth interface.The method is based on a reconstructed approximation space that is constructed by a patch reconstruction procedure.This approach creates an element patch for each element and solves a local least squares fitting problem to obtain a local high-order polynomial[26,28–30].Using this new space,we design the discrete scheme for the biharmonic problem under the symmetric interior penalty discontinuous Galerkin (IPDG) framework.

In penalty methods based on unfitted meshes,the small cuts around the interface may adversely affect the stability of the discrete system and hamper the convergence.Some stabilized strategies have to be applied to cure the effects,such as the ghost penalty method and the extended method,see [4,5,8,21,23,38] for some examples.Benefiting from the reconstruction,we can achieve arbitrary approximation accuracy with only one degree of freedom per interior element.Besides,we allow the interface to intersect the element in a very general way,and the stability in the cut element is ensured naturally by selecting a proper element patch for it without any extra stabilized method.

We prove the optimal convergence rates under the energy norm theL2norm,respectively.Numerical experiments are conducted to verify the theoretical analysis and show that our algorithm is simple to implement and can reach high-order accuracy.

The rest of this paper is organized as follows.In Section 2,we introduce the biharmonic interface problem and give the basic notations about the Sobolev spaces and the partition.We also recall two commonly used inequalities in this section.In Section 3,we establish the reconstruction operator and the corresponding approximation space.Some basic properties of the reconstruction are also proven in this section.In Section 4,we define the discrete variational form for the interface problem and analyse the error under the energy norm and theL2norm.In Section 5,we carried out some numerical examples to validate our theoretical results and show high-order accuracy of our method.Finally,a brief conclusion is given in Section 6.

2 Preliminaries

Let Ω⊂Rd,(d=2,3) be a bounded polygonal (polyhedral) domain with a Lipschitz boundary∂Ω.Let Γ be aC2-smooth interface that divides the domain Ω into two subdomains Ω0and Ω1,Γ=∂Ω0∩∂Ω1,see Fig.1 for an illustration.In this paper,we consider the following biharmonic interface problem

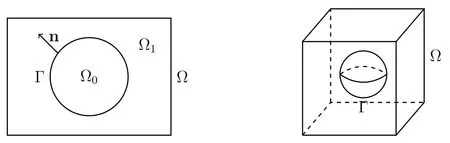
Figure 1:The sample domain for d=2 (left) and d=3 (right).

whereβis a positive constant function on Ω which may be discontinuous across the interface Γ.[[·]] denotes the jump operator,which is defined as

wheren0andn1denotes the unit normal on Γ orienting from Ω0towards Ω1andΩ1towards Ω0,respectively.

Given a bounded domainD⊂Ω,we follow the standard definitions to the spaceL2(D),L2(D)d,the spacesHq(D),Hq(D)dwith the regular exponentq ≥0.ForD0,D1⊂Rd,we define the Sobolev spaceHq(D0∪D1) as functions inD0∪D1such that,i=0,1,with the norm and seminorm

respectively.We assume that under some regular conditions of the dataf,g1,g2,a1,a2,a3anda4,the interface problem (2.1) admits an unique solution inH4(Ω0∪Ω1).We refer to [2] for detailed regularity results.

We denote byTha regular and quasi-uniform partition Ω into disjoint open triangles (tetrahedra).The grid is not required to be fitted to the interface.LetEhdenote the set of alld−1 dimensional faces ofTh,and we decomposeEhinto,whereare the sets of interior faces and boundary faces,respectively.We let

and defineh:=.The quasi-uniformity of the meshThis in the sense that there exists a constantν>0 such that,whereρKis the diameter of the largest ball inscribed inK.One can get the inverse inequality and the trace inequality from the regularity of the mesh,which are commonly used in the analysis.

Lemma 2.1.There exists a constant C independent of the mesh size h,such that

Lemma 2.2.There exists a constant C independent of the mesh size h,such that

wherePl(K)is the space of polynomial on K with the degree no more than l.

We refer to [3] for more details of these inequalities.

Further,we give the notations related to the interface.For any facee∈Ehand any elementK∈Th,we define

We make some geometrical assumptions about the mesh to ensure the interface is well-resolved by the mesh,which is commonly used in numerically solving interface problems [10,16].

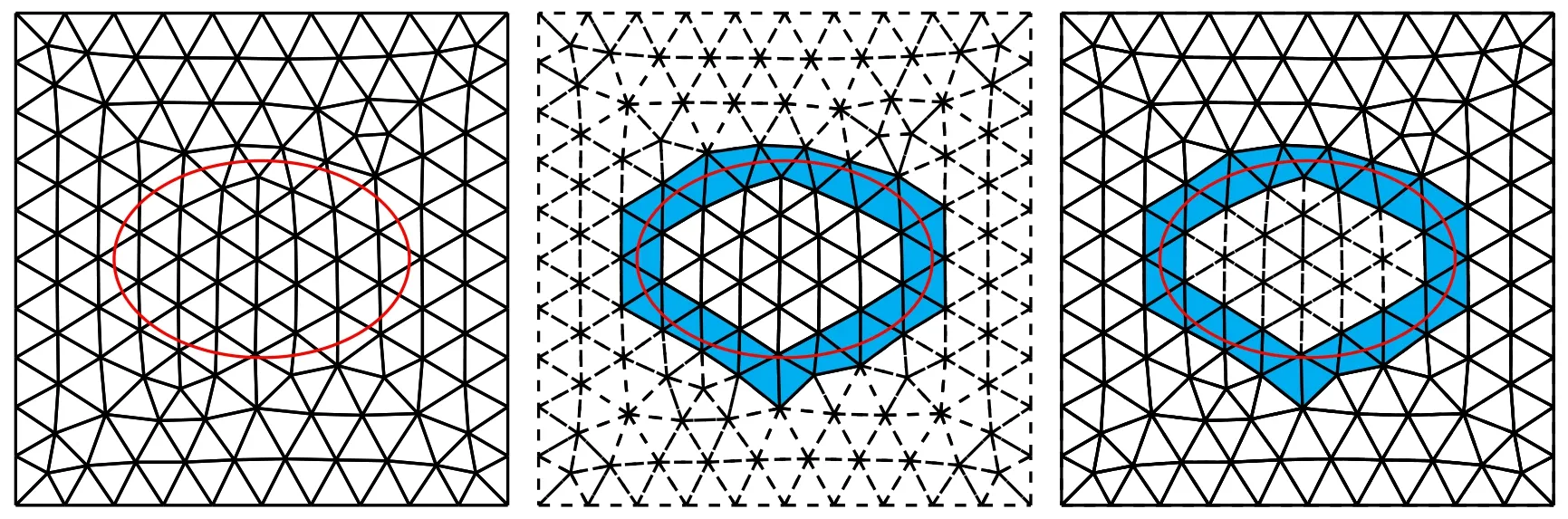
Figure 2:The mesh Th (left), (middle) and (right),the elements in (blue).

Such assumptions can always holds true when the mesh is fine enough.The Assumption 2.2 allows us to define two mapsM0(·) andM1(·) such that for any elementK∈Th,

whereis any chosen element that are in the Moore neighbours ofKand are included in Ωi.These maps will be used in the construction of the reconstruction operator.

Next,we introduce the trace operators that will be used in our numerical schemes.For,we denote byK+andK−the two neighbouring elements that share the boundarye,andn+,n−the unit out normal vector one,respectively.We define the jump operator [[·]] and the average operator{·}as

Fore∈,we letK∈Thsuch thate∈∂Kandnis the unit out normal vector.We define

ForK∈,we have already defined the jump operators in (2.2),the average operators are defined as follows.

Throughout this paper,CandCwith subscripts denote the generic constants that may differ between lines but are independent of the mesh size and how the interface intersects the mesh.

3 Reconstructed discontinuous space

In this section,we aim to construct the reconstructed discontinuous space for approximating the problem(2.1)by using a global reconstruction operator.The global operator which we denote byRhas two componentsR0andR1with respect to the sets.To obtain these operators,we employ a reconstruction process for each,i=0,1 that consists of three steps.First,we mark the barycenterxKfor every interior elementK∈as a collocation point,i=0,1,see Fig.3.

Figure 3:The collocation points in (left) and (right).

The final step is to solve a local constrained least squares fitting problem.The least squares problem resolves a polynomial of degreemfrom a piecewise constant function in,where

The constraint in(3.1)is crucial for proving the linear independence result in Lemma 3.1.We make the following geometrical assumption on the location of collocation points [26,27]:

Based on the local operators,we can further define two reconstruction operators piecewise as follows

Figure 4:Two basis functions inside the interface (left) and outside the interface (right).

Next,we will prove some approximation properties of the operatorRi(i=0,1).We first define a constant Λ(m,Si(K)) for every element patch [26],

Assumption 3.1 actually ensures Λ(m,Si(K))<∞,and we set

Proof.We define a polynomial space

Becauseεis arbitrary,the above inequality implies

From (3.6) and the constant Λ(m,Si(K)),it can be seen that

Combining all above inequalities,we conclude that

From the stability result (3.5),we can prove the following approximation property.

Lemma 3.3.For any K∈(i=0,1)and g∈Hm+1(Ω),there exists a constant C such that

Proof.By Lemma 3.2,we have

The caseq>0 will be proved by using the inverse inequality(2.4).Take a polynomial,we can obtain that

which completes the proof.

Remark 3.1.In the proof of Lemma 3.3,we have used the fact that for anyg∈Hm+1(Si(K)),there exists a polynomialp∈Pm(Si(K)) such that

These hold in condition thatSi(K) is star-shaped.We refer to [12] for the details.

From (3.7),it can be seen that the operatorRihas an approximation error of degreeO(hm+1−q) provided that Λmadmits an upper bound independent of the mesh sizeh.Under some mild assumptions about the element patch,we can prove that the constant Λ(m,Si(K)) has a uniform upper bound.

Assumption 3.2.For every element patchSi(K) (K∈Th,i=0 or 1),there exist constantsRandrwhich are independent ofKsuch thatBr⊂Si(K)⊂BR,andSi(K) is star-shaped with respect toBr,whereBρis a disk with the radiusρ.

Under the geometrical Assumption 3.2,we have the following result.

Lemma 3.4.For any ε>0,if

Proof.For the proof of this lemma the reader is referred to [24].

According to Lemma 3.4,to ensure the stability of the reconstruction operator,we are required to construct a large element patch to make the radiusras large as possible.The geometrical conditions can be fulfilled if the threshold #Sis larger than a certain constant which only depends on the mesh andm.We refer to [26,Lemma 6] and [27,Lemma 3.4] for the details of this statement.We list the value of #Sin our numerical experiments in Section 5.

Finally,we define a global reconstruction operatorRby combining two operatorsR0andR1.We choose two extension operators which extend the functions inHq(Ωi)toHq(Ω),q≥1.From [1,Chapter 5],we know that for anyw∈Hq(Ω0∪Ω1),there exist two operatorsEi:Hq(Ωi)→Hq(Ω) such that

For anyw∈Hq(Ω0∪Ω1),we defineRwas

whereχiis the characteristic function with respect to the domain Ωi.For the operatorR,we have the following local approximation error estimates:

Theorem 3.1.For any K∈,there exists a constant C such that

for any g∈Hm+1(Ω0∪Ω1).

Proof.The result directly follows from Lemma 3.3 and the definition of the extension operatorEi.

Remark 3.2.In this section,we have constructed a discontinuous polynomial spacebased on the global reconstruction operatorR.Since each element has at most one unknown,we can construct an arbitrary order space without increasing the degrees of freedom.This is in contrast to the normal DG space,which requires a large number of degrees of freedom on a single element for achieving high-order accuracy[22].From Theorem 3.1,the spacehas almost the same approximation property as the normal DG space of the same order as long as the constant Λmis uniformly bounded.Therefore,we can acquire high-order approximation with fewer degrees of freedom.

4 Approximation to biharmonic interface problem

We define the approximation problem to solve the biharmonic interface problem(2.1) based on the spaceconstructed in the previous section:Seekuh∈(m≥2) such that

The parameterµ1andµ2are positive penalties which are set by

The linear formlh(·) is defined forv∈Uh,

We introduce two energy norms for the spaceUh,

Before we start the error analysis,we first prove some trace inequalities,which play a crucial role in the following analysis.

Lemma 4.1.For any element K ∈,there exists constant C such that

Proof.The proof of this result is quite similar to that in [29,Lemma 2] and so is omitted.

Lemma 4.2.For any element K ∈,there exists a positive constant h0independent of h and the location of the interface such that ∀h≤h0,

See the proof of this lemma in [16,37].

We claim that the two energy norms are equivalent over the space.

Lemma 4.3.For any,there exists a constant C,such that

Proof.We only need to prove|||uh|||≤C‖uh‖DG.Fore ∈,we denote the two neighbor elements ofebyK+andK−.We have

By the trace inequalities (2.3) and (4.2),and the inverse inequality (2.4),we obtain that

which can immediately leads us to (4.4) and completes the proof.

Now we are ready to prove the coercivity and the continuity of the bilinear formBh(·,·).

Theorem 4.1.Let Bh(·,·)be the bilinear form with sufficiently large penalty η.Then there exists a positive constant C such that

Proof.From Lemma 4.3,we only need to establish the coercivity over the norm‖·‖DG.For the facee∈,letebe shared by the neighbor elementsK−andK+.We apply the Cauchy-Schwarz inequality to get that

for any∊>0.From the trace inequalities(2.3),(4.2)and the inverse inequality(2.4),we deduce that

Thus,we have

For the elementK∈,we apply the Cauchy-Schwarz inequality,the trace estimate(4.2) and the inverse inequality (2.4) to get that

which implies that

Combining the inequalities (4.6),(4.7),(4.9),(4.8) and (4.10),we conclude that there exists a constantCsuch that

for any∊>0,whereβmin>0 is the minimum value ofβ.We can let∊=βmin/(2C)and select a sufficiently largeηto ensure

which completes the proof.

Theorem 4.2.There exists a positive constant C such that

Proof.The continuity can be proved by directly using the Cauchy-Schwarz inequality,

which completes the proof.

Now we verify the Galerkin orthogonality to the bilinear formBh(·,·).

Lemma 4.4.Suppose u∈H4(Ω0∪Ω1)is the exact solution to the problem(2.1),and uh ∈is the numerical solution to the discrete problem(4.1),then

Proof.Sinceu∈H4(Ω0∪Ω1),we have that

Taking the exact solution intoBh(·,·),we have that

We multiply the test functionvhat both side of equation (2.1),and apply the integration by parts to get that

Thus,by simply calculating,we obtain that

which completes the proof.

Then we establish the interpolation error estimate toRunder the norm|||·|||.

Lemma 4.5.For0≤h≤h0and m≥2,there exists a constant C such that

Proof.From the definition of the extension operatorEiand Theorem 3.1,we can show that

fori=0,1.By the trace estimate (4.3),

The other trace terms in|||v−Rv|||can be bounded by the trace estimates(4.3)and(2.3) similarly,which completes the proof.

Now we are ready to present the a priori error estimate under|||·|||within the standard Lax-Milgram framework.

Theorem 4.3.Suppose the biharmonic interface problem(2.1)has a solution u∈Hs(Ω0∪Ω1),where s=max(4,m+1),m ≥2andΛm has a uniform upper bound independent of h.Let the bilinear form Bh(·,·)be defined with a sufficiently large η andbe the numerical solution to the problem(4.1).Then for h≤h0there exists a constant C such that

Proof.From (4.5),(4.11) and (4.12),we have that for anyvh ∈,

By the triangle inequality,there holds

Letvh=Ru,by the inequality (4.13),we arrive at

which completes the proof.

Ultimately,we prove theL2error estimate by the duality argument.Letφ ∈H4(Ω0∪Ω1) be the solution of the problem

and satisfies

We refer to [34] for the details of the regularity assumption.

From the Galerkin orthogonality (4.12) and the Theorem 4.3,we deduce that

We summarize what we have proved as the following theorem:

Theorem 4.4.Suppose the conditions in Theorem4.3hold true and the solution of the auxiliary problem(4.15)satisfies the condition(4.16),then we have

5 Numerical results

In this section,we conduct a series numerical experiments to test the performance of our method.For the accuracy 2≤m≤6,the penalty parameter and the threshold#Swe used in Examples 5.1,5.2,5.4 and 5.5 are listed in Table 1.For all examples,the jump conditionsa1,a2,a3,a4,the boundaryg1,g2and the right hand sidefin Eq.(2.1) are chosen according to the exact solution.The integrals on the interface and the curved domains like

in the numerical scheme are implemented by the PHG package [39].

Table 1:The η and #S used in 2D (left) and 3D (right) examples.

Example 5.1.We first consider a problem defined on the squared domain Ω=(−1,1)2with a circular interface inside it.The interface is described by the level function

see Fig.5.The exact solution is chosen by

with the coefficient to be

We solve the interface problem on a sequence of meshes with the sizeh=1/10,1/20,1/40,1/80.The convergence histories under the|||·|||andare shown in Fig.6.The error under the energy norm is decreasing at the speedO(hm−1)for fixedm.ForL2error,the speed isO(h2) whenm=2 andO(hm+1) whenm≥3.This results are coincide with the theoretical analysis in Theorem 4.3 and Theorem 4.4.

Figure 5:The interface and the mesh in Example 5.1.

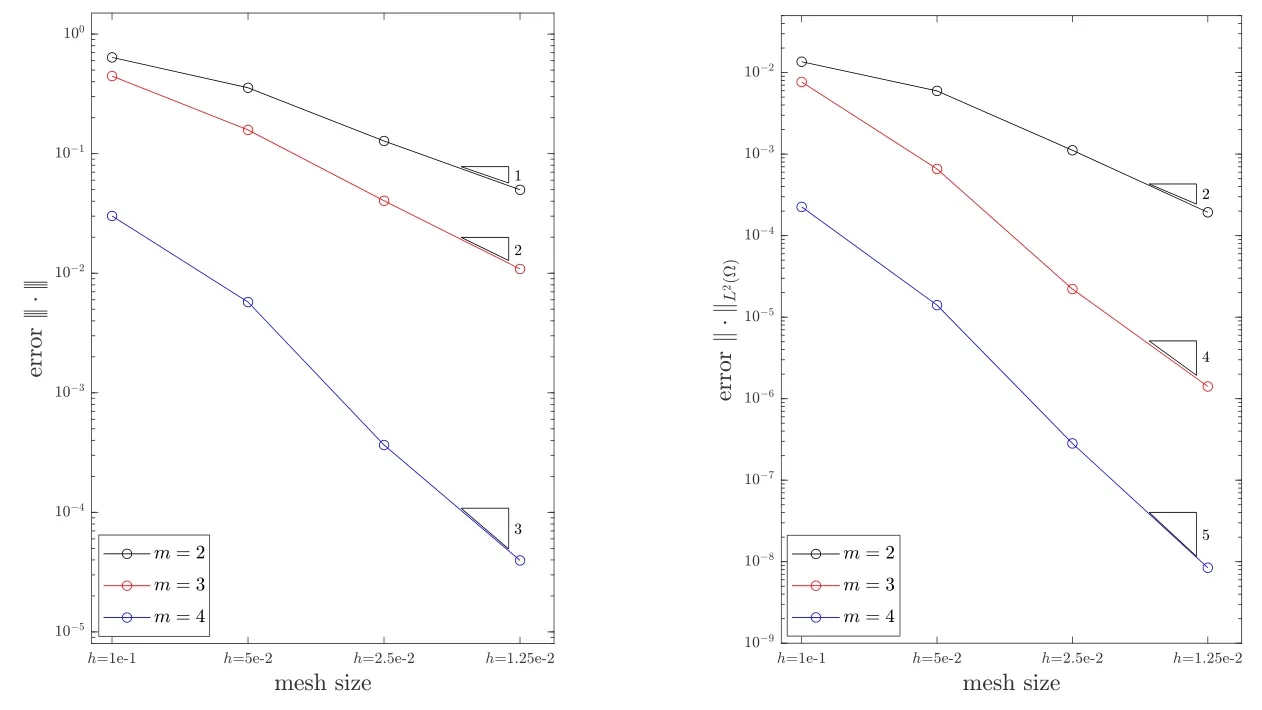
Figure 6:The convergence histories under the |||·||| (left) and the (right) in Example 5.1.

Example 5.2.We test the high-order approximation property in this example by solving a biharmonic interface problem on the squared domain Ω=(−1,1)2.The interface is still given by (5.1).The exact solution is taken as

The reconstruction ordermranges from 2 to 6.And the Ω is partitioned into triangle mesh with sizeh=0.15,0.075,0.0375,0.01875.We display the numerical results in Fig.7.It can be seen that all the convergence rates are consistent with our theoretical results and our method can achieve high-order accuracy by applying high-order reconstruction.

Example 5.3.In this example,we solve problem with a strong discontinuous coefficientβ.The problem is defined on the domain Ω=(−1,1)2with an ellipse interface(see Fig.8),

The exact solutionu(x,y) and the coefficientβis selected by

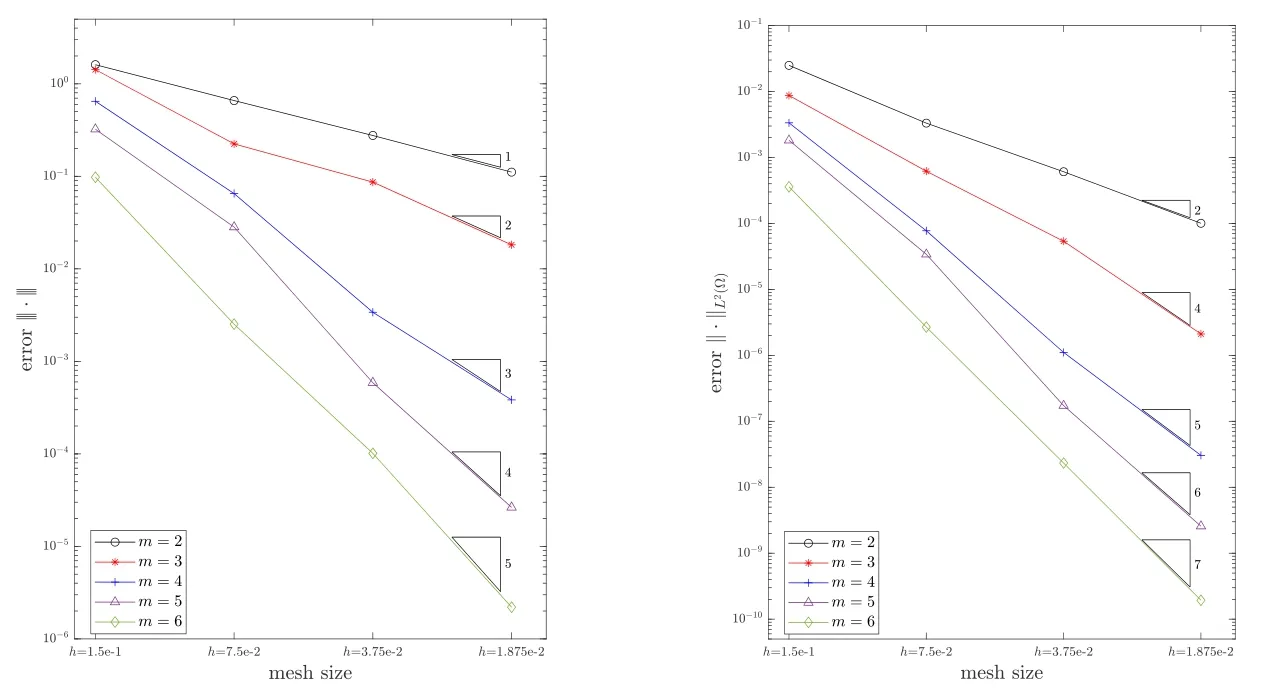
Figure 7:The convergence histories under the |||·||| (left) and the (right) in Example 5.2.

Figure 8:The interface and the mesh in Example 5.3.

We have to use large penaltyηto handle the large jump inβ,see Table 2.The numerical results presented in Fig.9 demonstrates that the error|||u−uh|||andare still tends to zero with the rates we predicted in Theorem 4.3 and 4.4.This example shows the robustness of the proposed method.

Table 2:The η and #S used in Example 5.3.

Example 5.4.In this example,we solve a problem on the domain Ω=(−1,1)2with a five-pointed star shaped interface.The interface is given by the polar coordinates(see Fig.10),

We choose the same analytical solution as Example 5.3 and the coefficient as

We use the initial mesh sizeh=1/10 and we successively refine the mesh three times for numerical tests.The convergence rates under the energy norm and theL2norm are plotted in Fig.9.We can observe from Fig.11 that the convergence rates under the|||·|||and theism−1 andm+1(except for the casem=2),respectively,which is still consistent with the theoretical results.

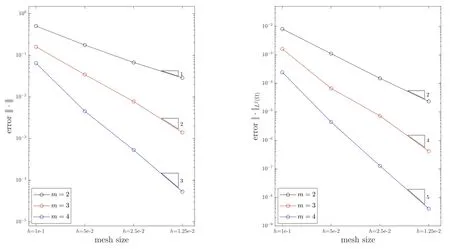
Figure 11:The convergence histories under the |||·||| (left) and the (right) in Example 5.4.

Example 5.5.We solve a three-dimensional biharmonic interface problem in this case.The computation domain is an unit cube Ω=(0,1)3containing a spherical interface in its interior (see Fig.12),

We select the coefficient and the exact solution as

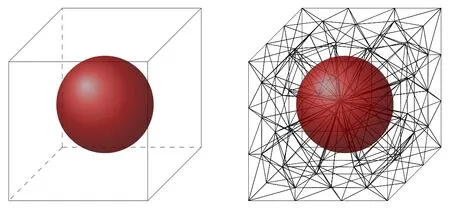
Figure 12:The interface and the mesh in Example 5.5.

We use the tetrahedra meshes generated by the Gmsh software [13].We solve the problem on five different meshes with the reconstruction orderm=2,3.The relationship between the cubic root of degrees of freedom and errors is shown in Fig.13,which is also clearly consistent with our theoretical predictions.

Figure 13:The convergence histories under the |||·||| (left) and the (right) in Example 5.5.

6 Conclusions

In this paper,we propose an arbitrary order discontinuous Galerkin extended finite element method for solving the biharmonic interface problem.The discrete formulation is obtained by a symmetric interior penalty method and the jump condition is enforced by Nitsche’s trick in a weak sense.The approximation space is constructed by a patch reconstruction operator and the number of degrees of freedom is independent of the approximation order.Our method is easily implemented and can achieve high-order accuracy.It is shown the optimal convergence rates for the numerical errors under the energy norm and theL2norm.We present a series of numerical experiments to verify the theoretical results and the efficiency of the proposed method.

Acknowledgements

The authors would like to thank the anonymous referees sincerely for their constructive comments that improve the quality of this paper.This research was supported by High-Performance Computing Platform of Peking University and National Science Foundation in China (No.11971041).