火电机组一次调频和二次调频响应功率数据剥离方法

刘子琦，刘 洋，李卫东，岳 涵，苏懿轩

（1.大连理工大学电气工程学院,辽宁省大连市 116024；2.国家电网有限公司东北分部,辽宁省沈阳市 110180）

0 引言

大规模新能源和高压直流输电接入挤压传统机组上网和调频空间,导致电力系统频率稳定问题愈发严峻［1-2］。保持充足的频率控制能力对安全稳定运行至关重要。

一次调频和二次调频是电网有功功率平衡实时控制的重要手段,两者控制目标和效果各异,其控制原理不同导致控制成本差异较大。在调频辅助服务市场中,两者一般分开竞价,并制定不同的补偿价格［3-4］。作为调频辅助服务供应商,获得收益的前提是所约定服务数量和质量的完成,而判断供应商是否保质保量地完成调频服务,需要机组调频控制性能评价作为依据［5-6］。显然,机组一次和二次调频控制效果需要分开评价［7］。目前,电网中传统火电机组容量占比最高,仍然是电网频率控制的主要资源。因此,对其调频控制性能做出准确评价十分必要。

机组一次和二次调频控制性能评价的本质是各自应发功率和实发功率的对比。火电机组一次和二次调频同时进行时,二者的调节效果均体现为机端输出功率变化,导致一次和二次调频功率彼此交织,难以区分。因此,要分别进行机组一次和二次调频控制性能评价,首先要分离一次和二次调频响应功率。

以往电网中,火电和水电等优质调频资源充足,机组调频控制性能评价需求尚不突出,因此,机组一次和二次调频响应功率的剥离方法比较粗略。文献［8-9］利用二次调频指令确定二次调频功率调整量,再从总调节功率中减去二次调频功率得到一次调频功率,其存在两个问题:1）认为二次调频是依据控制指令的瞬时响应,这种简化会造成评价标准的不合理；2）新型电力系统快速频率响应资源紧张,一次调频价值应高于二次调频,这种二次调频调节功率优先做法的不合理会导致评价结果的不准确。

从控制原理角度,火电机组一次和二次调频控制指令和响应环节不同,导致两者响应功率具有不同的时频特性,这为一次和二次调频响应功率剥离提供了一种途径。基于此,本文通过火电机组一次和二次调频响应控制过程差异性的解析分析,揭示了两者响应功率突出的二阶导数差异,据此进行功率剥离可解决已有算法在调频指令突变点附近剥离结果误差较大的问题。为进一步提升数据剥离精度,利用惯性环节参数拟合手段处理一次调频响应功率剥离问题,与原有基于线性思想的拟合策略相比,所提方法更符合一次调频控制实质,剥离结果更为合理。

1 火电机组一次和二次调频差异性分析

一次调频根据本地频差信号进行调速器自发响应,目的是限制系统频率的快速变化；二次调频根据上级调频控制指令调整机组发电功率运行点,目的是实现系统频率的无差调节。目前,大多数火电机组都接入自动发电控制（automatic generation control,AGC）回路,通过AGC 实现二次调频功能。火电机组一次和二次调频控制指令不同,执行环节各异,造成其响应功率具有不同的时频特性。然而,实际系统中无法分别测量机组一次和二次调频响应功率,不能直接进行数据分析。因此,需要分别建立描述机组一次和二次调频过程的响应模型,得到机组一次和二次调频响应功率数据,分析二者各自的数据特征。

需要注意的是,本章二次调频响应特性分析仅针对调频而言,不包含经济调度,突出机组对频差信号的动态响应特性。因此,在建模分析过程中,忽略最小出力约束和经济调度设定的基准运行功率点,仅对二次调频功率波动量进行数据分析。

1.1 一次调频与二次调频响应特性

火电机组一次调频由锅炉、汽轮机、调速器等多个环节协同完成,分析一次调频机理需包含上述关键模块。准确描述上述环节协同作用的模型通常为高阶复杂模型,难以解析求解。考虑到一次调频时间尺度一般为秒级至分钟级,故可忽略电磁过程的快动态和锅炉调节过程的慢动态,建立系统频率响应（system frequency response,SFR）模型［10］。基于SFR 模型描述一次调频响应功率的低阶开环模型如图1（a）所示。图中:Δfs为系统频差；Ppfr为一次调频响应功率；R为机组调差系数；FH为高压缸功率系数；TR为汽轮机再热时间常数。

图1 机组低阶开环调频模型Fig.1 Low-order open-loop frequency regulation model of unit

一次调频响应功率由系统频差和响应特性共同决定,其频域特性表示为:

式中:G1(s)为一次调频响应特性传递函数。

基于卷积定理,将式（1）的频域乘积计算形式转换为式（3）的时域卷积计算形式:

式中:“*”为卷积计算符号；t为时域连续时间；g1(t)为火电机组一次调频响应特性时域表达式。

由于机端测得的系统频差或功率序列为等间隔采样,故将式（3）表示为离散时间卷积计算形式:

式中:tz为时域离散时间；T为采样间隔；k为时间序列中采样点序号；[tz/T]表示不大于tz/T的最大整数。

对式（2）进行拉普拉斯逆变换,得到g1(t)为:

式中:δ(t)为单位冲激信号。

火电机组二次调频响应环节与一次调频相比,增加了制粉系统、锅炉汽水系统及机炉协调控制系统等,这些系统响应时间长、控制环节复杂［11］。为解析机组的二次调频响应特性,日常小扰动负荷情况下可以忽略锅炉蓄热变化,并将上述慢速动态过程简化为大时间常数惯性响应环节。不论系统二次调频控制模式如何复杂,其控制本质仍可以简化为对控制区域内频差信号的比例-积分控制［12］。综上所述,建立描述火电机组二次调频响应功率的低阶开环模型如图1（b）所示。图中:Kp和Ki分别为计算二次调频控制指令的比例和积分常数；Pagc为二次调频控制指令；TW为锅炉等效惯性时延常数；Psfr为二次调频响应功率,其频域特性如式（6）所示。

式中:G2(s)为二次调频响应特性传递函数。

由于TW远大于TR,以s=-1/TW为极点的瞬态响应分量衰减最慢,对系统动态响应性能影响最大。因此,可以进一步忽略TR,将式（7）简化为:

同理,可得二次调频响应功率的离散时间卷积计算形式:

对式（8）进行拉普拉斯逆变换,得到二次调频响应特性时域表达式g2(t)为:

式中:ε(t)为单位阶跃信号。

1.2 一次和二次调频响应功率时频分析

对比式（5）和式（10）,一次和二次调频响应特性相同点是都具有惯性环节,不同点是一次调频响应特性包含冲激信号项,而二次调频响应特性包含阶跃信号项。惯性环节对响应功率的影响体现在频域低通滤波特性,冲激信号和阶跃信号对响应功率的影响体现在时域比例和积分特性。因此,应该分别从频域和时域角度分析一次和二次调频响应功率数据特征。

1）频域特性

由于机组二次调频调节速度慢于一次调频,二次调频等效惯性时间常数TW大于一次调频等效惯性时间常数TR,导致二次调频响应特性的截止频率小于一次调频,即二次调频响应功率相比一次调频响应功率具有更强的低频特性。利用式（4）和式（9）计算得到单一火电机组1 h 内一次和二次调频响应功率时序图与频谱图,如图2（a）所示,可以明显看出一次和二次调频响应功率突出的频域差异性。

图2 系统频差及一次和二次调频功率时频分析Fig.2 System frequency difference and time-frequency analysis of primary and secondary frequency regulation power

但是,一次调频功率信号频谱分布过广,且一次和二次调频功率低频成分均占比很高,无法为一次和二次调频响应功率划分特定的频域区间范围。如果利用低频滤波器剥离二次调频响应功率,会带走实际属于一次调频功率的低频信号成分,导致一次调频调节功率剥离值偏小。因此,从频域角度无法准确区分一次和二次调频响应功率。

2）时域特性

由卷积计算特点可知:

式中:Δf-1s(t)为Δfs(t)的一阶积分。

由式（5）和式（10）可知,一次调频响应环节表现出比例特性,二次调频响应环节表现出积分特性。此外,分析图2（a）所示频差和功率时序图可知,一次调频响应功率随频差变化而快速变化,而二次调频响应功率则相对频差变化表现出滞后特性且变化较慢；在频率突变点处,一次调频响应功率能更快做出改变,而二次调频响应功率的变化则更为平缓。因此,可以从时域角度计算一次和二次调频响应功率各阶导数,分析两者差异性。利用式（4）和式（9）计算得到一次和二次调频响应功率一阶至四阶差分计算结果（标幺值）,如图2（b）、（c）所示。

图2（b）中,一次调频响应功率差分均值Ppfr,ave比二次调频功率差分均值Psfr,ave全部高出10 倍以上,一次调频响应功率差分方差Ppfr,var比二次调频功率差分方差Psfr,var全部高出100 倍以上,说明一次调频比二次调频响应功率的多阶导数变化速度更快,变化幅度更大,即一次调频响应功率并不包含特定的n阶趋势项。但对于二次调频响应功率,二阶以上差分数据的变化幅度明显下降,平均值更小且集中在零值附近；同时,二阶以上各阶差分数据统计结果区别并不显著。因此,以二阶差分作为二次调频响应功率时域特征做进一步分析。

图2（c）中,一次调频和二次调频响应功率二阶差分数据特征差异显著,其中二次调频响应功率二阶差分数值变化速度更慢,变化幅度更小且在零值附近,揭示了二次调频响应功率突出的时域二阶数据平滑性。因此,可以使用二阶趋势特征提取方法剥离二次调频响应功率。

综上所述,在对比一次和二次调频响应功率的频域和时域特性后,从频域角度无法为一次或二次调频响应功率各自划分确定的频域范围,而从时域角度,一次和二次调频响应功率具有突出的二阶差分变化差异。因此,最终选取二阶趋势特征提取方法区分一次和二次调频响应功率。

2 数据剥离算法设计

2.1 迭代优化模型的建立

为了便于后续说明,对本文常用信号量进行命名,如表1 所示。

表1 本文常用信号命名Table 1 Common signal naming in this paper

本文认为机端有功功率由一次调频和二次调频响应功率组成:

式中:w(t)为噪声数据,其组成以白噪声为主。

由于机组发电功率量纲通常在兆瓦级,机端功率数据的信噪比很大,在后续的功率数据处理过程中直接忽略了噪声数据的影响。

为分离一次和二次调频响应功率,现有方法多是通过建模准确表示一次和二次调频响应特性。然而,实际火电机组调频响应环节复杂,现有模型多根据研究问题进行不同程度的简化,导致模型响应功率与真实一次和二次调频响应功率间存在误差,但基于简化模型的响应功率仍可以作为实际功率的参考。对于一次调频功率,可以选取一次调频响应模型的响应功率Ppfr,m作为一次调频响应功率实际值Ppfr,a的参考。一次调频表现为惯性响应特性,因此,可以用惯性环节拟合弥补Ppfr,m和Ppfr,a之间的误差,上述关系可以表示为:

式中:g(t)为一次调频响应模型响应功率对实际响应功率的惯性环节冲激响应拟合函数；Ke和Te分别为惯性拟合比例和时间常数；g*(t)表示最优拟合函数；ΔPpfr,a(t)为拟合功率与实际功率间的实际差异。

当(Ke,Te)为最优拟合值(K*e,T*e)时认为一次调频功率剥离误差最小:

二次调频是根据二次调频指令的动态响应,因此,可以选取二次调频指令作为二次调频响应功率的参考,则二次调频响应信号实际值Psfr,a和模型值Psfr,m（即二次调频指令）之间的关系可表示为:

式中:ΔPsfr,a(t)为模型值与实际值之间的实际差异。

考虑到SCADA 采集到的功率数据均为等间隔采样信号,当采样间隔取1 s 时,得到一次和二次调频响应功率离散信号的3 个等式约束条件为:

式中:ΔPsfr,e和ΔPpfr,e分别为二次调频响应功率误差的剥离值和一次调频响应功率误差的剥离值。

2.2 数据剥离算法整体架构

基于前述模型,建立如表2 所示的数据剥离算法整体架构。表中:ΔPsfr,e[n]和(Ke,Te)均为迭代优化对象；ε1和ε2为收敛误差；i为迭代次数。先计算(Ke,Te)再计算ΔPsfr,e[n],ΔPsfr,e[n]和(Ke,Te)的变化使Psfr,e[n]和Ppfr,e[n]随迭代不断变化,不断逼近Psfr,a[n]和Ppfr,a[n]。

表2 数据剥离算法流程Table 2 Process of data separation algorithm

hp_filter 表示二阶趋势剥离器Hodrick-Prescott filter 函数,其定义如下:

该算法特点是可以通过改变α来分段剥离出二阶趋势项,α越小则分段越多,具体算法细则参考文献［13］。文献［14］指出,Hodrick-Prescott filter 算法具有单次特征提取结果精度不高的问题。为消除这一弊端,本文设计了如表2 所示的迭代分离算法结构,以提高二次调频响应功率剥离精度,与惯性环节参量拟合方法结合,达到进一步提高一次和二次调频响应功率剥离精度的目的。

2.3 数据剥离算法误差分析

为了评估一次和二次调频响应功率数据剥离算法效果,定义如下指标:

式中:epfr为一次调频响应功率剥离误差指标；esfr为二次调频响应功率剥离误差指标。

然而,epfr和esfr包含未知数据Ppfr,a和Psfr,a,无法直接使用。为评估数据剥离算法效果,需要将上述指标等效转化为可计算指标。为此,将式（18）代入式（22）得到:

由式（19）可知,二次调频响应功率剥离值由不变量Psfr,m和变化量ΔPsfr,e构成,将式（19）代入式（24）得到:

由式（25）可知,一次和二次调频响应功率剥离误差等价于二次调频响应功率残差量的剥离误差,即

将式（26）代入式（25）,得到esfr的另一种表示形式为:

由式（27）可知,esfr由整体误差中二阶趋势项的剥离精度决定,即当趋势特征提取函数收敛时,认为数据剥离算法收敛。因此,一次和二次调频响应功率剥离误差最小时需满足:

由式（24）可知,本文算法中一次和二次调频响应功率剥离误差相等,即一次和二次调频响应功率剥离结果同时收敛。分析优化过程发现,一次调频响应功率拟合参数(Ke,Te) 的逐次优化,令Ppfr,m[n]*g[n]逐渐逼近Ppfr,a,ΔPpfr,e随迭代次数不断减小,导致一次和二次功率剥离整体误差ΔPsfr,e[n]+ΔPpfr,e[n]中ΔPsfr,e[n]的比重不断增加,使二阶趋势项剥离结果更加准确,Psfr,m[n]+ΔPsfr,e[n]也更逼近Psfr,a[n]。因此,为便于收敛判断,本文算法选择(Ke,Te) 作为收敛判据,当(Ke,Te)逼近(K*e,T*e)时,ΔPsfr,e[n]逼近ΔPsfr,a[n],即得到了最接近真实值的一次和二调频响应功率剥离结果。

2.4 算法的通用性与适用性

对于火电机组一次调频和二次调频功率剥离算法的通用性问题,一方面,尽管不同类型火电机组的调频响应特性存在差异,对应的模型及参数也有不同,但本文是从火电机组一次调频和二次调频的核心差异,即二者的控制原理入手进行数据剥离,机组间的差异可以通过改变算法输入功率初始值的参考模型及其参数体现；另一方面,尽管算法输入功率初始值的参考模型为简化模型,但由于参考模型简化所带来的误差可通过数据剥离算法中惯性参数拟合和hp_filter 算法来弥补,这一简化使本文算法更专注于二者响应特性的差异,从而提高剥离精度。因此,所提方法可以通过改变输入功率初始值的参考模型与相关参数,而应用于不同类型的火电机组。

同一类型火电机组无论采用哪种调频响应控制策略（如机炉协调控制等）,电网调控中心对机组调频控制性能的评价均依据“两个细则”或其衍生管理规则进行,即基于统一标准考察机组有功出力的变化是否符合一次调频和二次调频指令的动作要求。上述标准不会随着机组机炉协调控制系统控制策略的不同而改变。因此,机组参与一次调频和二次调频的情况也只能以其输出功率变化作为评价依据,并不需要考虑其机炉协调控制模式。因此,所提方法可适用于不同调频响应控制策略的火电机组。

对于火电机组一次和二次调频功率剥离算法的适用性问题,在小扰动情况下,机组一次调频快速动作阻止系统频率下降,二次调频跟上恢复频率稳定,两者响应功率叠加交织,区分较为困难；在大扰动情况下,由于一次调频响应速度更快,其调节效果与二次调频之间的差异更为显著,更有利于二者响应功率数据剥离。对比大扰动和小扰动下的机组调频响应配合情况可知,两者并无本质区别,且小扰动情况下功率波动频繁,功率数据分离更加困难。因此,尽管本文是以小扰动情况为背景开展研究,但所提方法在大扰动情况下依然适用。

在实际应用时,本文算法仅在机组一次调频和二次调频同时动作时使用,需要根据SCADA 中对系统频差和AGC 指令（此处指二次调频指令）的记录,判断机组一次调频和二次调频的动作时刻,进而判断功率剥离时段。一般而言,相较于二次调频,一次调频的动作更为频繁。当机组未接收二次调频指令时,可以认为其功率的改变均为一次调频,故不需要功率剥离。否则,由于一次调频和二次调频同时发生,需要进行功率剥离。因此,可依据二次调频指令发布时刻进行功率剥离时段筛选与划分,每个时段的初始时刻为二次调频指令发布时刻,终止时刻二次调频指令不再变化。这样就可以保证机端功率数据中一次调频和二次调频动作的同时性。

3 算例分析

3.1 仿真数据源生成

日常扰动情况下,负荷波动形态符合奥恩斯坦-乌伦贝尔过程（Ornstein-Uhlenbeck process,OUP）［15-16］,其随机微分方程描述为:

式中:ΔP(t)为t时刻负荷波动的标幺值；τP为负荷波动平均反向时间；b为噪声值,可由扩散系数推导计算得到；ξ～N(0,1)。

为充分验证上述算法有效性,本文设计了如下2 个算例。

算例1:建立低阶火电机组调频模型并将一次和二次调频响应环节并联仿真,利用该模型能够测量一次和二次调频响应功率实际值,仿真模型如附录A 图A1 所 示。

算例2:建立单元火电机组调频模型［17-18］,模拟真实火电机组一次和二次调频过程,仿真模型如附录A 图A2 所示。为更贴近实际机组二次调频过程,上述模型均考虑二次调频指令间隔（4～8 s）和爬坡率约束。

一般而言,由于系统频率由一次调频和二次调频共同决定,因此,对机组一次调频和二次调频问题的研究需要考虑电网内各机组间的相互影响。数据剥离是面向机组的频率调节控制性能评价,属于事后分析范畴,此时系统内各机组的一次调频与二次调频控制指令和相应的响应过程均已明确,需要分析机组依照调频控制指令的执行情况,与机组间的相互影响无关。因此,采用单机模型进行算例仿真,即可验证所提方法的有效性与可行性。

基于上述机组调频模型和波动负荷模型进行算例验证。算例1 不设置机组基准运行点,算例2 设置单元火电机组基准运行点为0.8 p.u.,验证4 000 s 内一次和二次调频响应功率数据剥离效果。

3.2 一次和二次调频响应功率剥离算例

上述理论分析表明,以二阶趋势特征提取算法进行机端一次和二次调频响应功率分离会得到更好的效果,并给出了一次和二次调频响应功率剥离误差的近似解。为验证上述结论,算例1 设计了如下两个对比方案。

1）不同数据剥离算法效果对比

文献［8］提出利用二次调频指令直接作为二次调频响应功率,文献［9］利用分段线性拟合方法剥离二次调频响应功率信号。然而,本文依据二次调频响应功率解析表达式得出了二次调频响应功率信号具有二阶数据平滑性的结论。为验证本文方法的优势,在相同发电机组有功功率数据、相同一次和二次调频功率模型值条件下,对比上述3 种数据剥离方法效果。

2）实际误差与近似误差计算结果对比

文献［9］提出的功率剥离误差指标如式（22）所示,然而在实际系统中,无法得到一次和二次调频响应功率实际值,为此本文在2.3 节给出了剥离误差的近似解表达式。为说明本文所提近似误差的合理性,在相同发电机组有功功率数据、相同一次和二次调频功率模型值条件下,分析近似误差与实际误差的相关程度。

算例1 仿真结果如图3 所示,图3（a）使用一阶数据剥离算法l1_trend filter,图3（b）使用二阶数据剥离算法Hodrick-Prescott filter。从仿真结果可以看出,二次调频指令与Psfr,a[n]差异很大,因此文献［8］提出的分离方法并不合理；在其他求解条件相同的情况下,二阶数据剥离算法的剥离误差仅为一阶数据剥离算法的22.2%,同时在二次调频指令突变点附近,二阶数据剥离算法的剥离结果Psfr,e[n]与Psfr,a[n]波形更接近。因此,本文所提算法相比文献［9］提出的EPSCon 算法能更好地解决数据剥离问题。图3也给出了实际误差和近似误差随迭代次数的变化情况,可以看出,二者的变化趋势基本一致,当实际误差逼近最小值时,近似误差也逐渐收敛,因此以式（29）作为式（23）的近似解是合理的。

图3 低阶模型一次和二次调频响应功率数据剥离结果Fig.3 Data separation results of primary and secondary frequency regulation response power of loworder model

进一步验证算法有效性,设计算例2 基于单元火电机组调频模型,模拟真实火电机组一次和二次调频过程,本算例无法直接测量一次和二次调频响应功率实际值。由于二次调频指令与实际二次调频响应功率数据间差异较大,算例2 对比有二次调频指令和无二次调频指令作为二次调频模型值的数据剥离结果,得到仿真结果如图4所示。

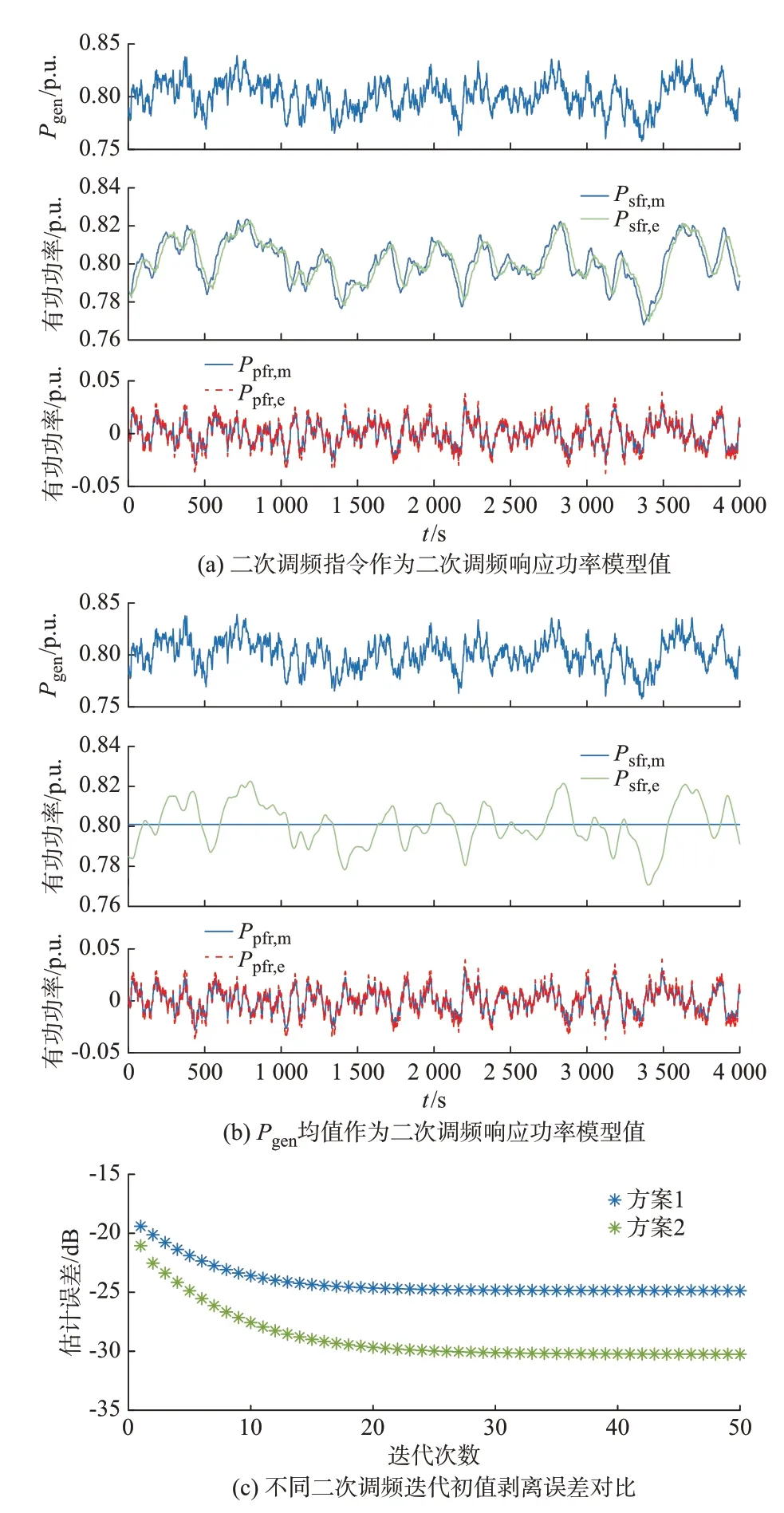
图4 高阶模型一次和二次调频响应功率数据剥离结果Fig.4 Data separation results of primary and secondary frequency regulation response power of high-order model

图4（a）使用二次调频指令作为二次调频响应功率模型值（方案1）,图4（b）使用Pgen均值作为二次调频响应功率模型值（方案2）,图4（c）为两种方案下的近似误差。从图4（a）可以看出,经过Hodrick-Prescott filter 的二次调频响应功率剥离结果与二次调频指令相比更为平滑,且有明显滞后,更贴近二次调频响应功率实际变化特点；一次调频响应信号相较SFR 模型值的幅值和相位发生细微变化。从图4（c）可以看出,使用Pgen均值作为二次调频响应功率模型值仿真计算速度明显提高,剥离结果误差下降。算例结果表明,若二次调频功率模型值与实际值间存在较大差异,会影响一次和二次调频响应功率的准确分离。

3.3 n阶多项式拟合算法效果对比

为进一步说明Hodrick-Prescott filter 算法对于解决一次调频和二次调频响应功率剥离问题的优势,增加n阶多项式拟合对比算例。将Hodrick-Prescott filter 替换为多项式拟合滤波器Savitzky-Golay filter［19］,对比分析多阶多项式拟合算法的一次和二次调频响应功率数据剥离效果。因为二次调频对应调节的是变化周期在分钟级的负荷,所以Savitzky-Golay filter选择的移动拟合数据段长度为61,仿真结果如图5 所示。从图5（b）可见,二阶拟合兼顾计算速度和拟合精度,在选取合适的拟合数据段长度时,二阶拟合能够达到很好的数据剥离效果。

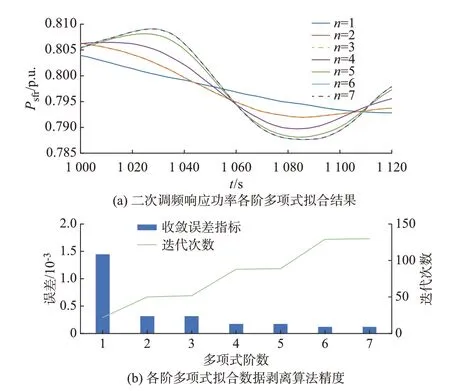
图5 多阶多项式拟合方式下的数据剥离结果Fig.5 Data separation results under multi-order polynomial fitting

4 结语

基于一次和二次调频的控制原理以及二者功率时间序列的时频特性,提出了一种从发电机输出功率中分离出一次和二次调频功率的方法。通过理论推导与仿真分析得出结论如下:

1）一次和二次调频响应功率时间序列各阶差分的分析表明,两者二阶差分的数值差异较大,使用二阶趋势特征提取算法Hodrick-Prescott filter,可更好地剥离出二次调频响应功率；同时,采用SFR 模型响应功率结合惯性环节冲激响应拟合方法剥离一次调频功率,与特征提取算法结合,可以进一步提升数据剥离算法的剥离精度。

2）与已有直接使用二次调频指令或一阶趋势特征提取算法l1_trend filter 相比,所提算法剥离均方误差指标分别下降98.9% 和77.9%；同采用Savitzky-Golay filter 进行三阶及以上分段多项式拟合相比,所提算法具有更快的计算速度。

3）理论分析表明,一次和二次调频响应功率剥离真实误差与趋势特征提取结果同时收敛,因此,可以利用相邻两次数据特征提取结果的差值作为近似误差评估数据剥离效果,以解决由于无法获取一次和二次调频真实功率值所导致的无法评估数据剥离算法效果的问题。

随着新型电力系统建设的不断深入,新能源发电比例将持续增加,传统火力发电机组将从发电主力变为电网辅助服务的重要提供者。为促进新能源消纳,火电机组将通过灵活性改造扩大稳定运行区间范围,与高负荷情况相比机组调频特性将发生显著变化。灵活性运行情况下的火电机组一次和二次调频功率如何准确剥离,是下一步的研究内容。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。