电动汽车应急充电设施布局规划方法

郭 栋，李娇娇，郑春燕，马鹏程，张同庆，李超超

（1.山东理工大学交通与车辆工程学院,山东省淄博市 255000；2.山东理工大学管理学院,山东省淄博市 255000）

0 引言

电动汽车以其清洁高效的突出优势与关键技术的快速发展完备,同时在国家战略的推进和政策的大力支持下［1］,实现了快速发展和广泛应用。但当前电动汽车续驶里程不足、充电设施发展不完善、充电形式单一等问题严重影响着电动汽车出行范围和用户的使用体验。此外,近40%的驾驶员经历过道路抛锚、充电不便以及需紧急充电的情形［2］。因此,在加强基础设施建设的同时,还应丰富充电形式以满足用户多样化的充电需求与充电情景,加快应急充电与便捷充电的发展,进一步促进充电设施与电动汽车的协调快速发展。

充电需求预测的研究是设施布局规划的重要前提,研究人员基于数学模型建立电动汽车出行的概率模型,蒙特卡洛法［3］、出行链理论［4］、累积前景理论［5-6］、灰色预测模型［7］、滚动预测［8］等都应用于充电需求预测。已有许多研究考虑用户充电行为选择［9］、城市功能区划分［10］、动态交通流［11］等普通场景下的多样充电需求预测,缺少缺电抛锚时应急充电需求、短时补电需求、偏远地区零散充电需求等特殊充电场景的单独研究。移动充电作为新的充电形式,以其灵活方便、占用资源少等独特优势弥补充电范围及便捷性,现有Mobi Charger、Spark Charge、大众移动充电机器人等成熟产品。针对移动充电的研究有:基于光伏-储能-充电供应链,结合物流网络,提出考虑配送时间与综合成本的移动充电配送路径优化模型［12］；考虑服务效率与服务成本,引入时间窗与多模式服务的移动充电服务模型［13］；基于静态车辆路径规划和调度的移动充电研究［14］。目前,针对移动充电的研究基本为充电速率或路径规划方面的研究,而对于移动充电相关设施点的布局研究较少,成为规模化应用新的阻碍点。充电设施布局作为电动汽车补能的核心基础设施［15］,基本目标是尽可能满足多样化充电需求,主要研究有:基于电动汽车出行特征与需求响应的多目标充电站布局模型［16］；基于充电站成本及用户充电行驶成本和充电时间成本最小的充电站选址定容模型［17］；多目标下充电站容量的优化配置［18-19］。综上所述,目前缺少针对应急充电需求的独立分析预测研究,以及基于应急充电需求时空分布特性、考虑多种影响因素的应急充电设施优化布局研究。

为满足电动汽车应急充电需求、偏远零散充电需求以及短时便捷补电需求,本文提出一种基于车、桩、路信息交互,应急电源配送与设施优化布局相结合的新型应急充电模式。首先,通过出行链理论及蒙特卡洛法对应急充电需求时空分布进行分析预测；然后,考虑应急充电需求时空特性与现有充电站分布特征,结合配送服务特点,利用遗传算法优化的Voronoi 图建立应急充电设施布局模型；最后,通过算例分析验证了应急充电需求的满足率及模型的有效性,实现了覆盖全面可靠、服务快速及时、充电便捷经济的应急充电。

1 电动汽车应急充电需求分析及预测

1.1 应急充电需求场景

应急充电需求主要指电动汽车因电量不足而具有较高道路抛锚风险或短时间内急需补电情景下的充电需求,主要由于驾驶员对充电时刻的误判或对未来行程中电量不足的担忧而产生,属于特定条件下的充电需求,主要针对场景为:1）车辆面临抛锚场景,即电动汽车因剩余电量不足无法到达充电目的地；2）碎片化时间充电场景,即利用短暂停留时间满足便捷补电需求。

考虑电动汽车剩余行驶里程、距离充电站距离等影响因素,应急充电需求条件为:

式中:Saim为电动汽车与最近充电站的距离；Sremain为电动汽车剩余行驶里程,根据汽车的单位里程内耗计算；SD为电动汽车与当前行程目的地的距离；Sremain,k-1为电动汽车在目的地k-1 时的剩余行驶里程；Sk为目的地k-1 与目的地k的距离；Tw,k为目的地k的停留时间；tmax和tmin分别为停留时间上下限阈值。

1.2 应急充电需求预测模型的建立

电动汽车应急充电需求的主要影响因素包括电动汽车出行规律、行驶规律和驾驶员充电决策。

1.2.1 电动汽车出行规律模型

电动汽车出行规律可用出行时刻、出行目的地、出行距离及目的地停留时长进行描述［20］。基于出行链理论分析出行者在时间和空间上的活动规律。

电动汽车首次出行时刻t0服从正态分布,其首次出行时刻概率密度函数为:

式中:μT、σT分别为电动汽车首次出行时刻均值、标准差,具体参数取值可参考文献［20］。

电动汽车出行距离近似为对数正态分布:

式中:fD（d）为出行距离的概率密度；d为出行距离；μD为平均出行距离；σD为出行距离标准差,参数取值可参考文献［21］。

出行目的地分为工作商务、日常生活和休闲娱乐3 类,不同类型区域停车时长满足广义极值分布［22］,式（5）、式（6）分别为工作区域、其他区域停留时长概率密度函数:

式中:f(∙)表示概率密度函数；x1为工作区域电动汽车停留时长；x2为其他区域电动汽车停留时长；z1、z2为相应区域停留时长标准化后的值。

1.2.2 电动汽车行驶规律模型

电动汽车行驶规律主要考虑电池容量、初始电池荷电状态（state of charge,SOC）、单位里程能耗的影响。

不同类型的电动汽车电池容量满足伽玛分布:

式中:Cp（l）为l类电动汽车的电池容量,由于本文研究对象是电动私家车,因此l=1；Γ(∙)表示伽玛函数；伽玛分布参数αl、βl具体取值可参考文献［23］。

电动汽车首次出行时刻的SOC 服从正态分布N（0.8,0.1）［24］。

电动汽车单位里程能耗基于平均车速的不同道路等级能耗因子模型进行计算,采用文献［25］提供的基于平均车速的不同道路等级能耗因子模型作为电动汽车单位里程能耗模型,如式（8）—式（11）所示。

式中:Ea、Eb、Ec、Ed分别为快速路、主干路、次干路和支路的能耗因子,单位为（kW·h）/km；v为路段平均速度,单位为km/h。

1.2.3 驾驶员充电决策

驾驶员充电决策主要表现为对充电起始时刻和充电结束时刻的选择［26］,充电起始SOC 和充电终止SOC 分别服从式（12）、式（13）所示的概率分布:

式中:x3为充电起始SOC；x4为充电终止SOC；μC、σC分别为电动汽车充电起始SOC 的均值、标准差,具体数值参考文献［27］。

1.2.4 基于蒙特卡洛法的应急充电需求模拟

一般充电需求预测模型为无差别的充电需求预测,没有针对充电需求类型进行细致研究,而电动汽车应急充电需求针对紧急缺电情形所产生的需求进行研究。两者虽大多采用蒙特卡洛进行模拟,但应急充电需求不具有普适性,此需求的产生是由于驾驶员对充电时刻的误判或对接下来行程电量不足的担忧,应急充电需求是在充电需求的基础上产生,是充电需求中的一部分特殊情况。

运用蒙特卡洛方法模拟电动汽车用户出行,获得电动汽车应急充电需求的时空分布,具体流程如图1 所示。假设城市日均电动汽车出行数量为N,且电动汽车用户日出行目的地不超过3 个（最终目的地为家）,并将家设为用户出行起始点与最终目的地。模型适用说明:模拟出行规律的数据来源为电动私家车数据,因此模型仅适用于电动私家车,不适用电动公交车、电动出租车和电动公务车等的出行类型。

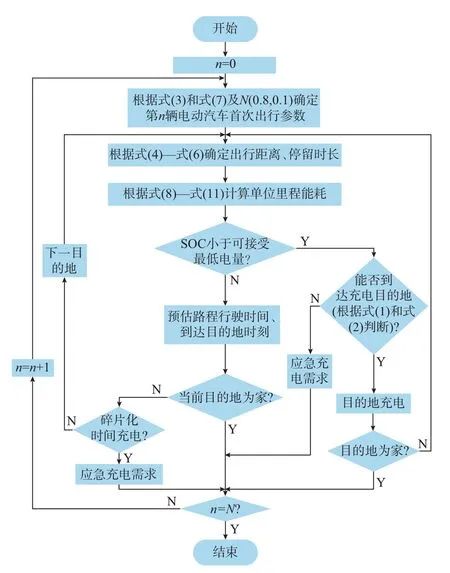
图1 蒙特卡洛法模拟应急充电需求流程图Fig.1 Flow chart of simulation of emergency charging demand based on Monte Carlo method

图1 所涉及的预估路程行驶时间ttravel和到达目的地时间tarrival计算如下:

式中:Stravel,f为出行距离,取决于式（4）；f取值为1 至4,分别代表快速路、主干路、次干路和支路；vf为对应道路的行驶速度；tfirst-travel为首次出行时间,取决于式（3）；tstay为停留时长,取决于式（5）和式（6）。

2 电动汽车应急充电设施布局规划模型

考虑应急充电需求时空分布特点、现有充电站分布、服务质量及综合成本,提出精准配送网络与应急充电设施布局网络优化结合的充电方案。

2.1 应急充电服务流程

近年来,城市配送行业运用线上线下结合、点对点配送模式迅速崛起,即用户线上下单、配送员线下点对点配送,具有便捷、灵活、高效等突出优势,且业务具备良好的可拓展性。本文提出了一种采用专员配送应急电源的应急充电服务模式,服务流程如图2 所示,电动汽车产生应急充电需求后,用户线上发起订单,系统依据需求点位置选取最合适的应急充电设施,并由服务专员将应急电源配送至需求点以提供充电服务,充电完成后由专员将应急电源送回原设施处,结束全部流程。

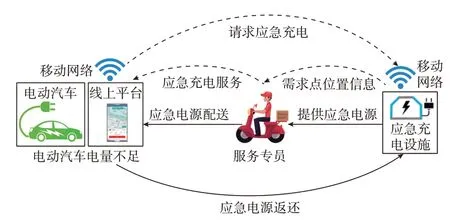
图2 电动汽车应急充电服务流程Fig.2 Process of emergency charging service for electric vehicles

应急充电设施主要由应急电源、光伏发电系统及监控管理系统组成,其中供电系统采用分布式并网光伏发电系统。应急充电设施通过光伏发电与储能为应急电源供电,实现光储充一体化,体现“新能源车充新能源电”。相较于传统充电站,应急充电设施具有成本低、建设难度小、占地面积小等突出优势,可与充电站配合以充分发挥其独特功能。

2.2 应急充电设施布局规划模型的建立

电动汽车应急充电设施布局主要考虑选址及定容问题。选址主要满足可靠性、及时性、经济性,突出与现有公共充电站的协调关系；定容主要考虑应急电源工作周期与需求数量的关系。

2.2.1 目标函数的建立

建立结合配送模式的应急充电设施布局规划模型,首先做出以下假设:1）不考虑路网中道路坡度和交叉口的影响；2）服务专员对路网及充电需求点位置完全了解且选取耗时最短的配送路径；3）各应急充电设施中应急电源数量保持相对恒定,即应急电源使用后归还至原设施或各设施间相互交换数相同。

应急充电设施布局规划目标为以尽可能高的服务水平满足应急充电需求,服务水平以用户等待时间成本表示,并同时兼顾设施的建设运行成本。因此,以用户等待时间成本和应急充电设施建设运行成本作为目标函数:

式中:F为应急充电设施综合成本；C1为用户等待时间成本；C2为应急充电设施建设运行成本；α1、α2为权重系数,根据经济性与服务水平综合选取。本文主要考虑服务水平,取α1=1.2,α2=0.8。

1）用户等待时间成本

用户等待时间包括应急电源的配送时间和充电时间,其成本为:

式中:dij为应急充电设施j到其服务范围内充电需求点i的行驶距离；vD为平均行驶速度；Tec为应急充电平均服务时间,主要受用户主观选择和应急电源电池容量影响；ω为城市出行单位时间成本；ny为使用年数,主要受应急电源使用寿命影响；J为备选应急充电设施集合,j∈J；δj为应急充电设施j服务范围内的充电需求点集合。

2）应急充电设施建设运行成本

应急充电设施建设成本包括应急电源成本和设施成本,其中设施成本主要为光伏系统成本,运行成本主要包括设备维护和人工成本。年运行成本通常为建设成本的20%。因此,应急充电设施建设运行成本为:

式中:fp为工商业分布式光伏电站造价,单位为万元/kW；qj为单个设施内应急电源数量；Pw为单个应急电源所需的光伏发电功率；fe为单个应急电源价格。

2.2.2 选址及定容约束

应急充电设施的布局约束主要考虑选址约束与定容约束。选址约束主要包括与充电站等基础充电设施的相对位置约束、各应急充电设施间的距离约束、应急充电需求点与最近应急充电设施的最大距离约束。定容约束主要考虑每个应急充电设施服务范围内的最大应急充电需求数与应急电源工作周期关系约束。

1）应急充电设施与充电站相对位置约束

应急充电设施应与充电站相配合,需对应急充电设施与充电站的相对位置关系进行约束,确保电动汽车在完成应急充电服务后,剩余电量能够到达附近充电站或目的地进行电量补给,且应保证两者具有一定距离,以充分发挥设施功能。充电站、应急充电设施和应急充电需求点满足如下关系式,示意图见附录A 图A1。

式中:r为应急充电设施服务半径；R为应急充电设施与最近充电站的最大距离；dstr为电动汽车与应急充电设施的直线距离；L为电动汽车与充电站的直线距离；m为充电站与应急充电设施间的直线距离；ζ为城市道路非直线系数,路网的平均非直线系数一般为1.15～1.2［28］。

当应急充电需求点与充电站的距离最远,即m=R、L=R+r时,满足车辆应急充电后可到达充电站,则满足所有应急充电需求。从而,有:

2）各应急充电设施间的距离约束

为保证布局的可靠性,需满足应急充电需求全覆盖,即任意应急充电需求i都存在应急充电设施j为其服务:

为满足布局的可靠性与经济性,相邻应急充电设施间距应具有如下约束:

式中:r1、r2为相邻两个设施的服务半径；D为两个相邻设施间的距离。

3）应急充电需求点与最近应急充电设施的最大距离约束

为保证布局的及时性,需对每个应急充电需求点与最近应急充电设施的最大距离进行约束,本文采用服务专员按一定平均速度配送,可转化为最大配送时间约束:

式中:Tij为服务专员从应急充电设施j到其范围内的应急充电需求点i的时间；Tmax为最大配送时间。

4）应急充电设施定容约束

应急电源的服务能力受应急电源工作周期Tp（接受订单至充电结束为一个周期）的限制。为保证任意时刻应急电源数量都不少于该时刻发生的应急充电需求数量,根据应急充电需求的时空分布获得在Tp内应急充电需求最大数量GT,应急电源的配置数量Nm应满足Nm≥GT。

应急电源工作周期包括配送响应及路程耗时TD、充电服务时间Tsc、送回响应及返程耗时Tr和应急电源自身充电时间Tc,其中,配送耗时和返程耗时可视作相同,即TD=Tr。因此,有

若某个应急充电设施服务范围内,GT=3,则其最少需配置3 个应急电源。例如,恰有3 次应急充电需求发生时,其使用关系见附录A 图A2。

此外,考虑设备故障等特殊原因,在最大需求数量上额外增加10%,单个应急充电设施内应急电源配置数量qj为:

2.2.3 基于Voronoi 图和遗传算法的求解策略

应急充电设施布局关键是确定应急充电设施服务范围内的应急充电需求数量。本文以应急充电设施位置为生长点生成Voronoi 图,得到各应急充电设施服务范围,同时将Voronoi 图与遗传算法结合以提高全局搜索能力。具体流程如图3 所示。

图3 基于Voronoi 图和遗传算法的求解流程图Fig.3 Flow chart of solving based on Voronoi diagram and genetic algorithm

在使用Voronoi 图和遗传算法进行求解时,遗传算法初始参数设置为:种群规模P=2 000,遗传迭代数Gmax=200,交叉概率CCP=0.9,变异概率MP=0.01,适应度值为年综合成本的倒数（1/F）。将每种应急充电设施布局方案作为个体,应急充电设施的位置和数量作为个体的基因。

应急充电设施数量Ne预估:

式中:Nmax、Nmin分别为应急充电设施的最大和最小数量；| |I为规划区域一天内应急充电需求数量；Qmax、Qmin分别为应急电源最大和最小配置数；μ为平均服务速率,即每个应急电源单位时间完成服务的车辆数；Ts为应急电源平均每天有效充电服务时间；表示向上取整。

3 算例分析

本文以中国山东省淄博市张店区为例进行仿真分析,验证模型的有效性并为其他城市未来应急充电需求的研究及设施建设布局提供参考。

3.1 应急充电需求分析

3.1.1 电动汽车出行仿真

对电动汽车出行进行模拟仿真,获取始发地、目的地及行驶速度等信息。通过Python 获取各居民小区信息（具体见附录B 表B1）,作为出行始发地和最终目的地；通过百度地图应用程序编程接口（application programming interface,API）获取各类型兴趣点（points of interest,POI）数据及其位置,POI 数据点类型主要包括:充电站、工作商务、日常生活、休闲娱乐,数据点空间分布见附录A 图A3；通过百度地图API 实时路况获取各路段拥堵信息,得到不同拥堵程度下各等级道路平均车速,具体见附录B 表B2。

3.1.2 出行仿真结果及分析

根据张店区电动汽车发展趋势预测,设置5 年后电动汽车样本数量为8 万辆［29］。运用蒙特卡洛法依据上述流程对全部电动汽车进行一天的出行仿真,共产生1 851 条应急充电需求（如附录A 图A4所示）,应急充电需求主要出现在各类POI 点的集中区域、商业经济中心和车流密集区。充电需求时间分布图如图4 所示,应急充电需求数量为先升再降、再升再降过程,出现“双高峰”现象,与用户出行高峰期相吻合。

图4 应急充电需求时间分布Fig.4 Time distribution of emergency charging demand

应急充电需求数据中,多数为用户碎片化时间场景充电,占69.5%；23.4%的应急充电需求为道路应急场景产生,主要是由于用户最低充电SOC 值偏好过低。因此,最低充电SOC 值偏好是产生应急充电的重要影响因素,当最低SOC 值偏好为5%～10%时最易产生应急充电需求,其具体关系见附录A 图A5。剩余应急充电需求的产生主要与用户的长距离出行和偏远充电需求有关,但本次仿真区域较小,用户产生长距离出行的可能性较低或无充电站覆盖的偏远点较少。因此,此类应急充电需求比较低,仅占7%。

3.2 应急充电设施布局规划分析

3.2.1 模型参数设置

首先,对张店区路网拓扑化,具体拓扑图见附录A 图A6。应急充电需求位置分布见附录A 图A7。

设工商业分布式光伏电站造价fp为6 元/W；应急电源单价为0.2 万元/个；服务专员平均行驶速度vD为30 km/h；最大配送时间为0.167 h；应急电源平均服务速率μ为1 辆/h；应急充电单次服务时间Tec为0.16 h；应急电源平均每天有效充电服务时间Ts为1 h；城市道路非直线系数ζ为1.2；城市出行时间成本为0.003 万元/h；单个应急电源充电所需的光伏发电功率Pw为7.2 kW/个；应急电源的电池容量为3.5 kW·h,放电功率为18 kW,充电功率为7 kW。

3.2.2 应急充电设施数量优化

由上述仿真可知,单位时间内应急充电需求数量为19～250 个,则应急充电设施数量满足Nmin=3,Nmax=15。使用年数n主要考虑应急电源电池的使用寿命,因此计算前5 年综合成本。不同应急充电设施规划数量的5 年内各成本见附录B 表B3。

图5 为不同应急充电设施规划数量的5 年综合成本曲线,随着应急充电设施数量的增加,5 年综合成本先减后增,当设施数量为10 座时5 年综合成本最低,为4 625.90 万元。其中,随着设施数量的增加,建设运行成本不断升高,而用户等待时间成本呈下降趋势,主要是由于建设运行成本随设施数量的增加而增高,而每个设施对应的服务范围减少,配送路程缩短,用户等待时间成本降低。

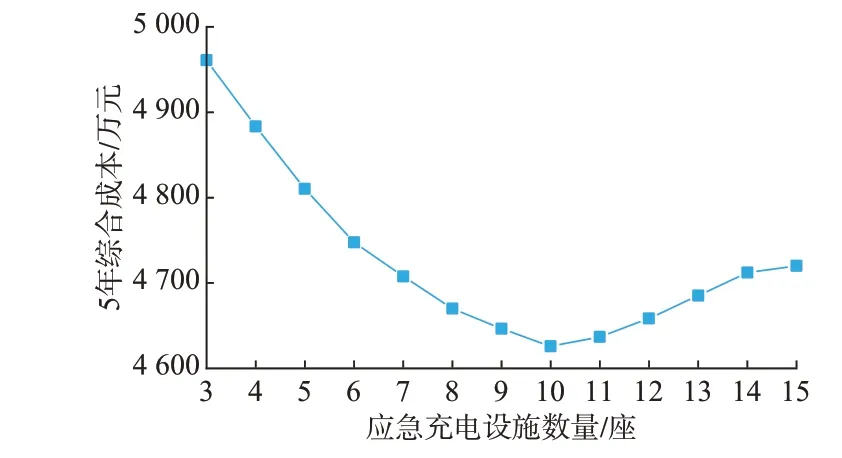
图5 应急充电设施5 年综合成本曲线Fig.5 Comprehensive cost curve of emergency charging facilities for 5 years

3.2.3 应急充电设施最优位置和容量

以S1～S10表示10 座应急充电设施,求解得到各设施选址位置和服务范围,如附录A 图A8 所示。图6 为Voronoi 图多边形等效圆范围,其中:红色圆点表示充电设施位置,以红点为圆心,蓝色圆表示服务范围；绿色三角表示较为紧凑充电站的等效集中位置；黑色数字表示路段节点。由图6 可知,应急充电设施位置布局均匀合理,高度契合应急充电需求的时空分布特性,与现有充电站相辅相成,实现应急充电需求的全面覆盖,满足可靠性原则。

图6 Voronoi 图多边形等效圆范围Fig.6 Polygon equivalent circle range of Voronoi chart

表1 为应急充电设施最终布局规划结果,其中,应急电源平均配送时间为6.6 min,用户平均等待时间为16.6 min,应急充电服务时间小于30 min,满足及时性原则。特别的,应急充电设施S2、S9和S10处的应急电源数量较多,主要是由于其处于商业经济中心,车流量密集,且周围充电站服务范围有限,因此,易在出行高峰期产生大量应急充电需求,此外,用户在该区域目的地短时停留较为频繁,易产生较多的短时便捷补电需求。

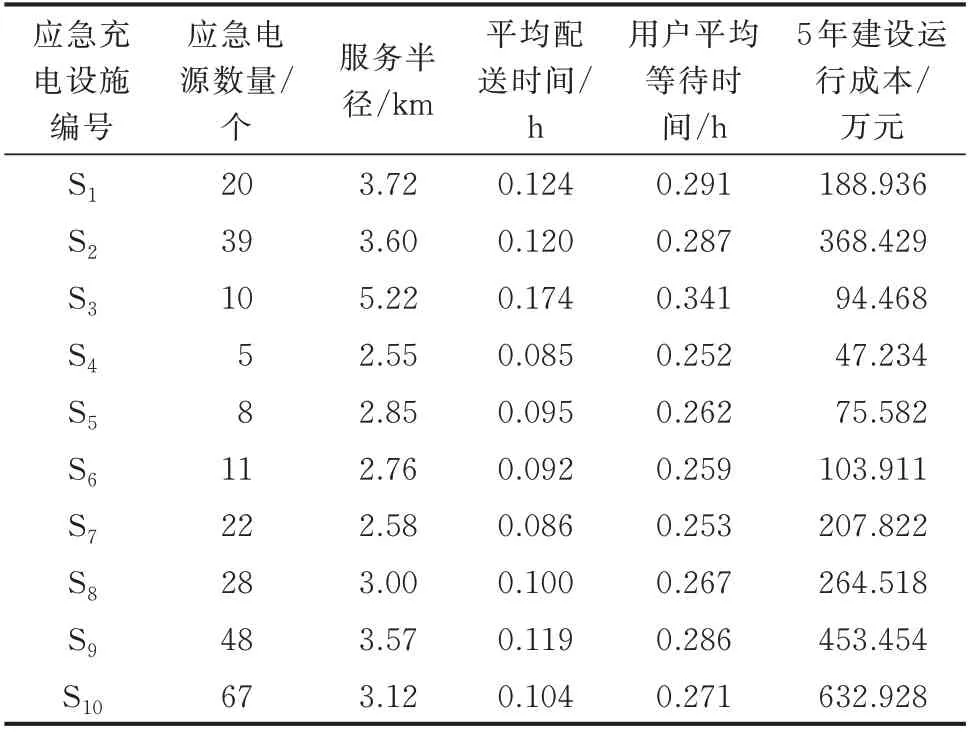
表1 应急充电设施最优布局规划结果Table 1 Optimal layout planning results of emergency charging facilities

3.2.4 结果验证

加入应急充电设施布局建立新的充电网络,以相同仿真条件再次对电动汽车出行进行仿真,以进一步验证模型的有效性和结果的合理性。仿真共产生了1 675 个应急充电需求,其中31 个未满足,在保证服务水平的基础上,应急充电需求满足率为98.15%,验证结果如表2 所示,未满足的应急充电需求分布见附录A 图A9。应急充电设施布局可有效满足应急充电需求,应急充电设施布局模型具有一定的有效性和合理性。

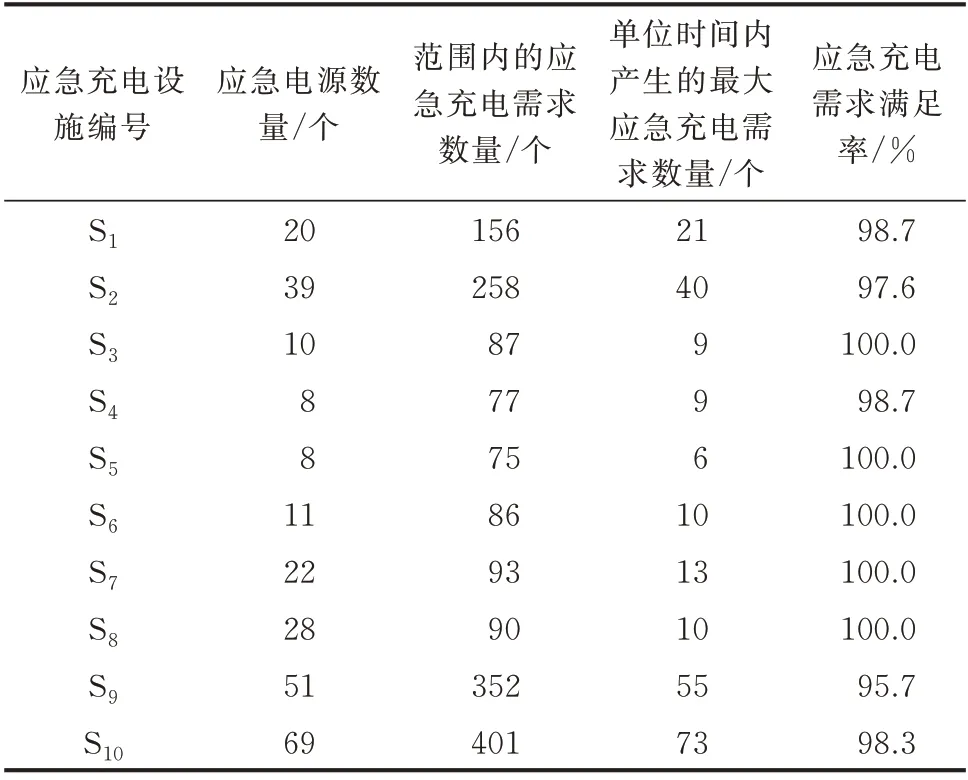
表2 应急充电设施规划模型仿真验证结果Table 2 Simulation verification results of emergency charging facility planning model

表2 中部分设施存在应急充电需求率非100%,导致少量未满足应急充电需求的主要原因是:应急充电设施布局优化中是以满足绝大多数区域应急充电需求而建立,针对区域边缘的零散应急充电需求再建立应急充电设施是不合理的；从应急电源数量与单位时间最大需求数来看,部分时段出现了应急充电设施服务范围内单位时间产生的应急充电需求超过了配置的应急电源数量,导致无移动电源可进行配送服务,如S1、S2、S4、S9和S10。

4 结语

当前电动汽车充电设施发展不完善,有关电动汽车充电研究较少考虑紧急、短时、便捷等特殊充电需求,无法满足电动汽车应急充电需求、偏远地区零散充电需求以及短时便捷补电场景。为解决以上问题,本文开展了以下工作:

1）提出了基于出行链理论和蒙特卡洛法的应急充电需求时空分布预测方法。考虑电动汽车行驶规律、出行规律和驾驶员充电决策,对应急充电需求时空分布进行分析预测。研究发现,应急充电需求的空间分布高度契合POI 数据点分布,时间分布吻合用户出行时间规律,曲线亦呈现“双高峰”。

2）采用应急电源精准配送与设施布局优化相结合的新型充电模式。利用应急电源独立供电和可移动性的优点,并充分发挥现有精准配送服务模式点对点的优势,将应急电源精准配送与设施布局优化相结合,提出了一种具有便捷、经济、灵活等特点的应急补电模式,可与充电站相协调形成更加优化的电动汽车补电网络。

3）兼顾应急充电设施服务水平和建设运行成本,建立以设定综合成本最少的应急充电设施布局模型,提出精准配送网络与应急充电设施布局网络优化结合的充电方案。本文建立的优化布局模型能够有效覆盖区域内产生的应急充电需求,提出的配送服务模式可有效缓解应急充电问题,且能实现短时到达要求,弥补应急场景下的碎片化补电需求。

本文主要考虑私家车的出行过程,未考虑出租车、网约车和公共用车的出行特征,电动汽车的出行过程还会受到出行日期的影响。今后研究工作中可扩展研究对象以及其他出行场景,更好地为新能源汽车提供应急充电服务。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。