发电企业参与容量市场的纳什-主从博弈模型
2023-08-31卢治霖杨鑫和
卢治霖,尚 楠,张 妍,陈 政,杨鑫和,李 沛
(南方电网能源发展研究院有限责任公司,广东省广州市 510663)
0 引言
伴随新一轮电力体制改革的稳步推进,中国电力市场化改革取得显著成效[1]。中国南方区域电力市场于2022 年8 月23 日启动试运行,电力现货交易覆盖南方五省区,标志着中国统一电力市场体系进入新阶段[2]。当前,中国各省区电力市场中普遍存在寡头市场主体[3],即某个或多个发电企业集团在省内装机占据绝大多数市场份额,例如,广东省、浙江省最大的发电企业集团在省内的装机占比分别约为30%[4]、50%[5],次位发电企业集团的市场份额远低于最大发电企业。寡头市场主体的存在,将对各市场主体的竞价行为、市场的出清结果造成显著影响。容量市场作为一个远期市场,其出清结果将为各类型电源投资提供价格信号。然而,寡头主体的存在将扭曲容量市场价格信号,影响市场正常健康发展[6]。因此,有必要对发电企业参与容量市场的博弈竞价问题开展研究,分析寡头发电企业主体对容量市场出清结果的影响。
研究发电企业参与容量市场博弈竞价的难点在于对发电企业之间的博弈关系与发电企业和容量市场的交互机理进行建模。文献[5]针对容量市场的投资决策问题建立双层均衡模型,对寡头容量市场主体的策略行为进行了深入分析。文献[7]构建了面向容量机制与古诺寡头竞争的三阶段电力市场均衡模型框架,进一步研究了能量市场及容量机制中发电企业的策略性行为对电力交易的影响。文献[8]提出了一个拓展的多视角模型,用以分析包含需求响应用户的零售商在批发市场与容量市场的策略性报价行为。文献[9]分别采用两主体离散博弈模型与扩展的连续博弈模型来分析发电主体的竞争行为,验证了简单的容量市场设计存在鼓励发电企业提供虚假报价的风险。文献[10]以新爱尔兰电力市场为例,分析了市场主体策略性竞价对市场出清结果的影响。文献[11]基于双寡头案例,采用纳什-古诺均衡模型分析了电力市场与天然气市场的交互机理。然而,发电企业参与容量市场的博弈竞价问题是典型的双层优化问题,即各发电企业在模型上层相互竞价,并与下层容量市场出清问题进行交互。各发电企业的投标决策不仅相互影响,还会受到容量市场模拟出清结果的影响。上述文献所提出的模型均难以在描述市场主体相互竞争的同时理清市场主体与容量市场运作的交互关系。因此,本文构建了多领导者纳什-主从博弈模型来描述发电企业参与容量市场的策略性竞价问题。
研究发电企业参与容量市场博弈竞价的另外一个难点在于对所提多领导者纳什-主从博弈模型的求解。由于主从博弈模型在数学上具有较强的非线性和非凸性,故其均衡点的存在性和唯一性很难得到证明[12],难以通过多项式的方法直接获得问题的解析解[13]。文献[14]基于非线性高斯-赛德尔方法,利用对角化技术解决了虚拟电厂与配电公司间的多领导者博弈问题。类似地,文献[15]利用对角化算法求解能源市场中虚拟电厂的策略性竞价问题。但文献[14-15]需要反复迭代计算,仿真耗费时间过长,容易出现不收敛的情况。因此,本文提出采用共享约束法[16]对所提多领导者纳什-主从博弈模型进行修改,并基于KKT(Karush-Kuhn-Tucker)最优性条件原理[17]将模型转化为广义纳什均衡问题[18],再根据势博弈理论[19]求解模型的全局纳什均衡解。
本文对容量市场运行机理进行了详细介绍,并为发电企业参与容量市场博弈竞价构建了多领导者纳什-主从博弈模型。在模型上层,各发电企业通过模拟其他市场主体的决策与容量市场的运作情况,最大化参与容量市场的净利润。在模型下层,电力交易中心根据各发电企业的报价情况出清容量市场,并将市场出清结果反馈给各发电企业。
1 容量市场运行机理
容量市场机制将机组可用装机容量作为交易标的,通过市场竞争形成容量补偿价格。容量市场中买方为系统运营商,卖方为容量资源提供商,包括存量机组与待建机组。系统运营商根据负荷预测、可靠性要求等形成容量需求曲线,卖方申报容量资源数量和价格,市场运营机构以最小化容量购买成本得到容量市场出清结果,容量购买费用最终由所有用户分摊。目前,美国PJM、纽约及英国、法国等已应用容量市场机制。
通常,容量市场交易会比交付年提前若干年开展,主要流程包括容量定额、资格审查、主市场拍卖、二级市场拍卖、容量交付、容量费用结算[20],如图1所示。在容量定额环节,由英国市场运营商(NGESO)负责对维持系统长期可靠性标准所需的容量开展评估,结合容量评估结果、系统尖峰负荷的预测值,确定容量市场的需求规模。

图1 英国容量市场体系框架Fig.1 Framework of capacity market system in UK
在资格确认和拍卖环节,NGESO 根据市场准入条件启动资格审查,确定允许参与容量市场的容量供应商,获得准入的容量供应商可以参与由NGESO 组织的比交付年提前4 年的主拍卖市场(一级市场)。容量拍卖的中标主体将签订“容量合约”,该合约为容量供应商提供了相对稳定的收益,相应地,容量供应商须承担在交付年内按要求提供电能的义务,未能履约的容量供应商将面临罚款。
在主容量市场拍卖与实际容量履约间,市场参与者可通过二级市场交易追加容量拍卖过程,如容量供应商根据自身发电供应能力追加持有的容量合约以获得更高的收益,或适当售出容量合约以避免因延迟建设或计划外维护而产生的违约罚款。
在容量交付环节,竞标成功的市场主体(存量机组与待建机组)将在交付年获得相应的报酬,同时需要履行在交付年遵照NGESO 调用指令提供电力的义务,承担违约罚款的责任。
在费用支付方面,容量市场的费用通常由售电商承担,并依据其在交付年内电能量市场的售电份额进行分摊。容量费用由售电商经结算机构支付给容量供应商,如果容量提供者受到违约罚款,该罚款也将经过结算机构支付给售电商。
在主拍卖市场中,容量供应商在市场中报量报价,形成容量供给曲线,电力交易中心则根据容量定额情况形成容量需求曲线,两曲线交点则形成容量市场出清结果。以英国容量市场为例,其需求曲线由3 段组成[21],如图2 所示。容量需求曲线由价格上限、净成本、目标容量、容量最小值、容量最大值这5 个关键参数决定。其中,目标容量为预估交付获得可靠性标准的最优容量水平,净成本则表示新容量对应的合理成本。

图2 容量市场需求曲线Fig.2 Curves of capacity market demand
根据上述容量市场的运作机理,本文以英国容量市场模型为基础,进一步构建多领导者纳什-主从博弈模型来分析发电企业参与容量市场的博弈竞价问题。
2 发电企业参与容量市场竞价问题分析
本章将详细分析如何构建多领导者纳什-主从博弈模型来描述发电企业参与容量市场的投标竞价行为。具体而言,各发电企业在多领导者纳什-主从博弈中担任领导者的角色,最大化自身参与容量市场的净利润;而电力交易中心作为跟随者在下层负责出清容量市场。发电企业参与容量市场的多领导纳什-主从博弈模型具体结构如图3 所示。
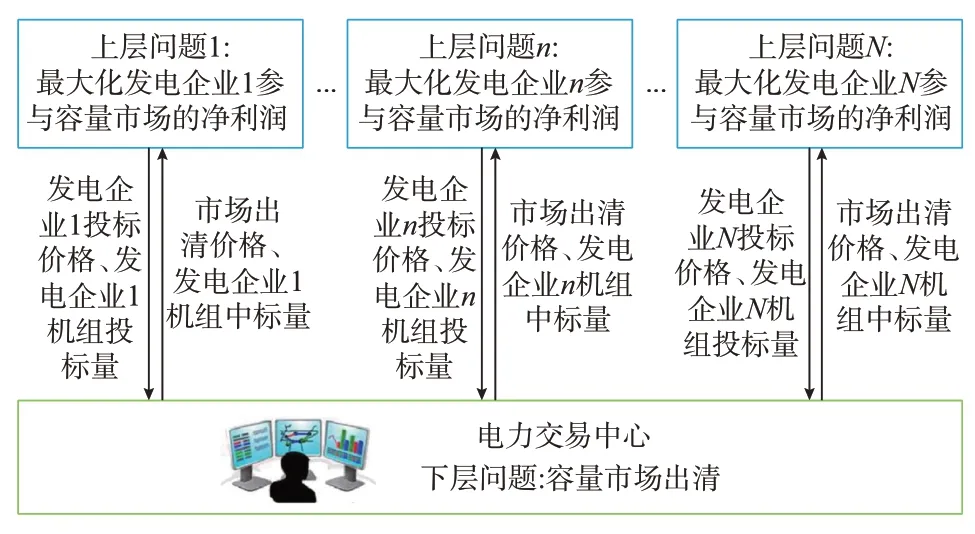
图3 发电企业参与容量市场的纳什-主从博弈模型框架Fig.3 Framework of Nash-Stackelberg game model for power generation enterprises participating in capacity market
根据图3 可知,在本文所构建的纳什-主从博弈模型中,各领导者(即发电企业)在模型的上层通过制定策略性的市场竞价策略来最大化其参与容量市场的净利润。然后,发电企业将投标价格和投标量等信息分别传递给下层问题,即容量市场出清问题。最后,电力交易中心负责对下层容量市场进行出清,并将出清结果进一步反馈给上层的各发电企业。
2.1 上层问题:最大化各发电企业参与容量市场的净利润
2.1.1 上层目标函数
式中:Nn,i为发电企业n存量机组数;λc为容量市场的出清价格;Pen,i为发电企业n存量机组i在容量市场的出清量;Cen,i为发电企业n存量机组i的单位容量成本缺额;Pen,i,max为发电企业n存量机组i的装机容量为发电企业n待建机组数;Pdn,m为发电企业n待建机组m在容量市场的出清量;Cdn,m为发电企业n待建机组m的单位容量成本缺额;Pbn,m为发电企业n待建机组m的投资容量。式(1)中第1 部分表示发电企业n存量机组在容量市场的净利润,第2 部分则表示发电企业n待建机组在容量市场的净利润。
2.1.2 上层约束条件
2.2 下层问题:容量市场出清
2.2.1 下层目标函数
下层问题的目标函数为容量市场总剩余最大,即向用户提供容量收入与机组提供容量成本的差值最大,如式(7)所示。为便于模型处理分析,本文将容量需求曲线按阶梯报价进行近似处理。
式中:Nd为容量需求的报价阶段数为第d段容量需求曲线对应的容量报价;Dcd为第d段容量需求曲线对应的出清容量;Nn为参与容量市场的发电企业数。
2.2.2 下层约束条件
1)容量平衡约束
式(8)表示市场中所有发电企业的存量机组出清容量与待建机组出清容量之和应与总容量需求相等。
2)容量出清约束
式中:Dcd,max为第d段需求容量的出清上限。式(9)表示发电企业n存量机组i的出清容量上下限约束;式(10)表示发电企业n待建机组m的出清容量上下限约束;式(11)为第d段需求容量的出清约束。
2.3 纳什-主从博弈模型的紧凑形式
对于特定的策略性领导者发电企业n(n=1,2,…,Nn)而言,纳什-主从博弈问题也可以看作双层问题,相应的紧凑形式如下:
对于跟随者,w求解如下问题:
式中:xn和x-n分别为领导者发电企业n和其他领导者的决策向量;w为跟随者的决策向量。式(12)和式(13)分别表示领导者发电企业n双层模型的目标函数fn和约束条件gn;式(14)和式(15)分别表示跟随者的目标函数z与约束条件p。
本文将上述多领导者纳什-主从博弈问题表示为δ。在δ中,领导者n在式(13)的约束下,通过调整其决策变量xn来最大化自身目标函数fn。不等式约束式(13)对于各领导者而言独立存在,相互不影响。此外,各领导者优化问题的解xn也必定影响跟随者决策w。因此,跟随者基于领导者的决策,在不等式(15)的约束下最小化其目标函数z。
3 求解方法
由于博弈问题δ具有高度非线性和非凸性[22],均衡点的存在唯一性很难得到证明,甚至无法求解获得该博弈问题的均衡解。多数情况下,多领导者纳什-主从博弈问题δ的双层均衡解不存在。因此,本文采用共享约束法扩展博弈问题δ的可行域,修改后的模型可以求解获得比原模型更多的均衡解[16]。在此基础上,利用势博弈求解问题δ的全局纳什均衡解。
3.1 共享约束法修改纳什-主从博弈模型
本文所提多领导者纳什-主从博弈模型可以通过共享约束法转化为广义纳什均衡模型,如图4 所示。在共享约束法中,各领导者都复制一个下层跟随者问题,并通过下标进行相应的标识化。此时,各领导者都有对应的下层问题。然后,各领导者将自己的下层问题共享给其他领导者,使各领导者都有Nn个下层问题。
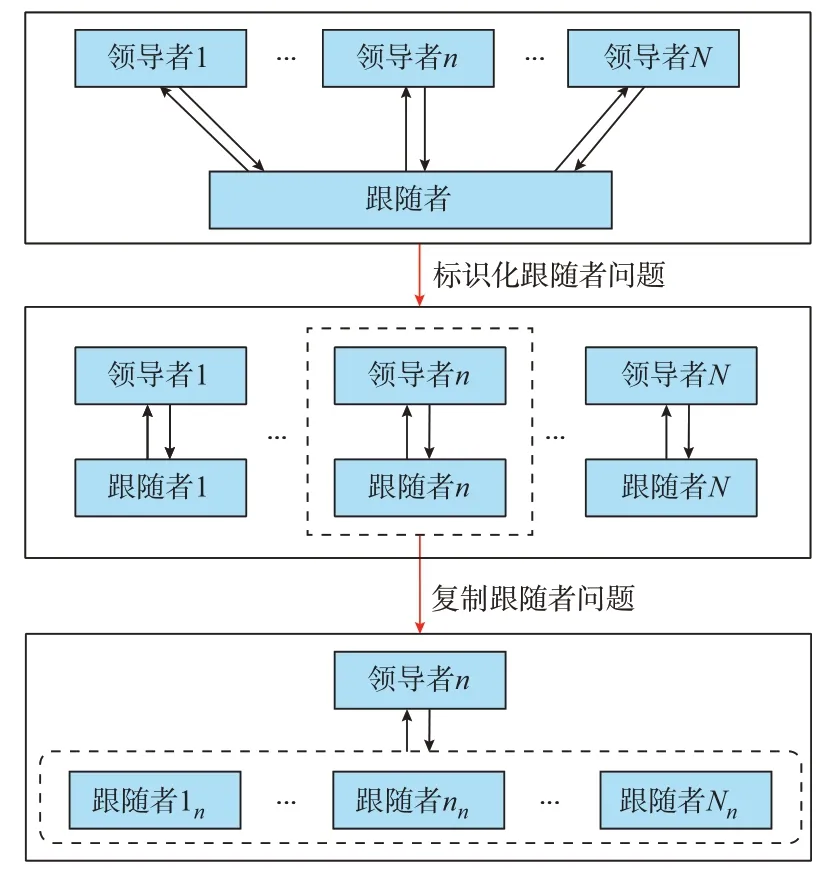
图4 共享约束法修改纳什-主从博弈问题框架Fig.4 Framework of shared-constraint approach for modifying Nash-Stackelberg game problem
采用共享约束法修改后的博弈问题δ如式(16)至式(19)所示。
对于跟随者k,有
式中:k=1,2,…,Nn;wn为领导者n对跟随者决策的猜想;zk为标识化后的跟随者目标函数;pk为标识化后的跟随者约束。跟随者的每个变量对于各领导者n都进行标识并复制,即各领导者都对跟随者的均衡情况做出自己的猜想。因此,领导者n的问题由其余领导者的决策x-n以及它们对于各跟随者均衡决策的猜想wk来进行参数化。本文将领导者n求解式(16)至式(19)所示带有共享约束的博弈问题设定为δae。
在博弈问题δae中,由于跟随者模式是凸问题,可用KKT 条件对式(18)、式(19)表示的跟随者问题进行代替。博弈问题δae转化为式(16)、式(17)和式(20)至式(22)所示的广义纳什均衡模型:
式中:k=1,2,…,Nn;vk为式(19)的对偶变量;∇wk表示对wk进行求导;“⊥”表示两个向量垂直。
3.2 势博弈理论求解δae的全局纳什均衡解
为求解博弈问题δae的全局纳什均衡解,引入了势博弈的概念。对于一个广义纳什均衡博弈问题,存在如式(23)所示的势函数π,使得对于所有n、xn、x-n、wn、w-n和其他任一决策向量、均满足式(24),则该广义纳什均衡博弈问题可转化为势博弈问题。
式中:x为领导者决策向量。
对于如式(16)和式(17)所示的广义纳什均衡模型,本文将其重构成势博弈模型,如式(25)、式(26)所示。
式中:Fae为满足式(17)、式(20)至式(22)的所有约束索引集。
进一步,本文分别运用大M 法[23]和强对偶定理[24]处理KKT 条件互补约束式(22)中的非线性项和目标函数式(25)中两个变量相乘的非线性项。至此,本文将多领导者纳什-主从博弈模型转化为混合整数线性规划问题,该问题可通过常见的商业求解器进行求解。
4 算例分析
4.1 测试数据概况
本文采用中国某省实际数据进行仿真,以验证所提模型的有效性。本文设定容量供给商包含传统燃煤、燃气、核电、水电机组四大类型机组,各类型机组容量占比如图5 所示。其中,存量机组容量为81.8 GW,待建机组容量为57.5 GW,总计为139.3 GW。

图5 各类型机组容量占比Fig.5 Capacity ratio of each type of unit
本文设定容量供给商机组由三大发电企业进行运营管理。各发电企业的待建机组系数αn、βn分别设定为0.7、0.8;容量市场价格上限为55 万元/MW;参考机组成本缺额为40 万元/MW;容量市场的目标容量为128 MW。
4.2 算例结果分析
本文为分析寡头发电企业主体对容量市场出清结果的影响,设计了6 种不同存量机组占比情况的方案进行详细对比,具体情况如下:
方案1:各发电企业存量机组的占比相等,均为33.3%。
方案2:发电企业Ⅰ、Ⅱ和Ⅲ存量机组的占比分别为35%、33%和32%。
方案3:发电企业Ⅰ、Ⅱ和Ⅲ存量机组的占比分别为40%、40%和20%。
方案4:发电企业Ⅰ、Ⅱ和Ⅲ存量机组的占比分别为40%、30%和30%。
方案5:发电企业Ⅰ、Ⅱ和Ⅲ存量机组的占比分别为50%、25%和25%。
方案6:发电企业Ⅰ、Ⅱ和Ⅲ存量机组的占比分别为80%、10%和10%。
4.2.1 充分竞争环境
图6 给出了充分竞争环境下各发电企业在不同方案的容量市场投标情况。可以看到,方案1 与方案2 中各发电企业的存量机组占比较为接近,市场中不存在寡头发电企业主体,各主体难以通过市场力在容量市场中谋取超额利润。因此,各发电企业均以机组单位容量成本缺额进行报价,不同容量区间中各发电企业的报价分布较为均匀。
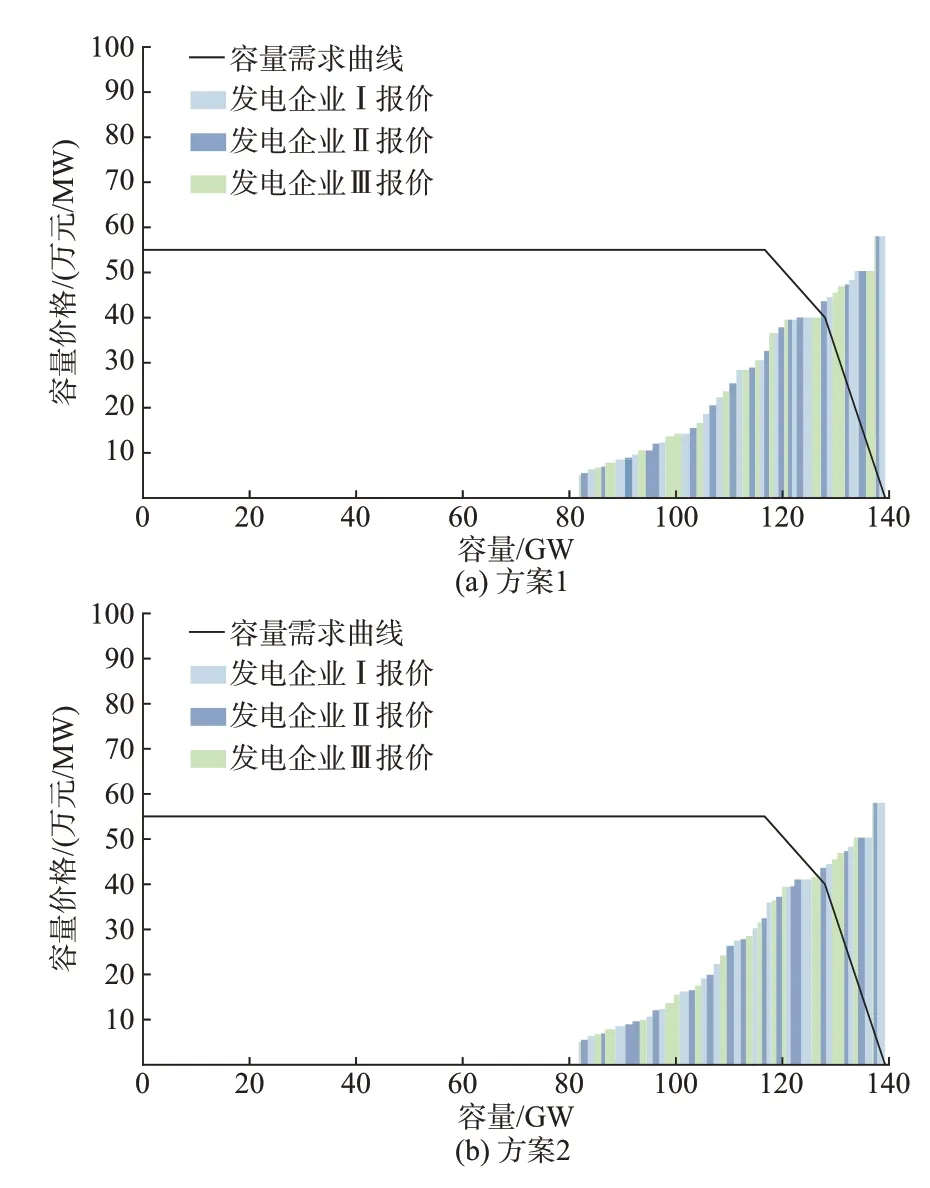
图6 充分竞争环境下不同方案的容量市场报价对比Fig.6 Comparison of capacity market quotations with different schemes under fully competitive environment
表1 则给出了充分竞争环境下不同方案的容量市场出清情况对比。可以看到,由于容量市场处于充分竞争状态,市场出清价格和出清容量均与容量市场预设的目标值较为接近。因此,当市场中不存在寡头主体时,发电企业间不同存量机组的占比变化并不会对容量市场出清结果造成显著影响,社会福利维持在较为理想的水平。
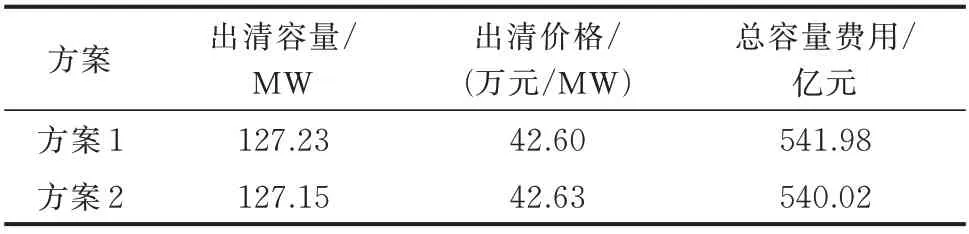
表1 充分竞争环境下不同方案的容量市场出清结果对比Table 1 Comparison of clearing results for capacity market with different schemes under fully competitive environment
4.2.2 垄断竞争环境
图7 给出了垄断竞争环境下各发电企业在不同方案的容量市场投标情况。可以看到,寡头市场主体以较高份额的存量机组占比抢占了市场中绝大部分的可投资待建机组资源。具体表现为寡头市场主体在容量市场中进行策略性报价,通过牺牲中标容量在拍卖中的单价收益来换取更高的市场出清价格,从而实现收益最大化。根据方案4、5、6 的对比可知,伴随寡头市场主体的存量机组份额上升,该主体拥有更强的市场力,对出清价格的抬升效果更加显著。另一方面,通过方案3 与4 的对比可知,寡头市场主体数量的增多在一定程度上制约了主体的策略性报价行为,削弱了寡头主体市场力的影响。

图7 垄断竞争环境下不同方案的容量市场报价情况对比Fig.7 Comparison of capacity market quotations with different schemes under monopolistic competitive environment
表2 给出了垄断竞争环境下不同方案的容量市场出清情况对比。可以看出,寡头市场主体的策略性报价行为极大影响了容量市场出清结果,4 个方案中社会福利均出现不同程度的损失。具体表现为寡头发电企业利用市场力,通过抬高容量报价和牺牲出清容量来控制市场出清价格。伴随着寡头主体的存量占比份额逐步上升,市场出清容量逐步减少,出清价格逐步上涨,总容量费用逐步抬升。当寡头主体的存量机组份额占足够优势后,出清价格被抬升至市场报价上限55 万元/MW,与充分竞争市场环境下的价格相比,上升幅度达29.11%。方案6中,市场终端用户获得出清容量仅为方案1 的91.72%,却需要多支付18.43%的容量费用。显然,寡头发电企业的策略性竞价行为将造成社会福利的损失。

表2 垄断竞争环境下不同方案的容量市场出清情况对比Table 2 Comparison of clearing results for capacity market with different schemes under monopolistic competitive environment
表3 给出了垄断竞争环境下不同方案的各发电企业收益情况。可以看出,寡头主体数量的减少加剧了寡头主体的垄断行为,但当寡头主体的存量机组占比份额未能形成绝对优势时,策略性的报价行为未能带来直接收益,相反,将会造成待建机组成本无法完全回收的情况。与方案3 发电企业收益情况对比,方案4 和5 中寡头主体的待建机组补贴率均少于100%,即待建机组在容量市场中的收益无法覆盖其建设成本。当寡头发电企业存量机组占比高达80%时,其待建机组可以通过容量市场回收建设成本,但待建机组补贴率仍少于方案3 中双寡头的场景。显然,寡头主体的策略性报价行为将严重损害其待建建组的容量收益。

表3 垄断竞争环境下不同方案的各发电企业收益情况对比Table 3 Comparison of power generation enterprise incomes with different schemes under monopolistic competitive environment
另一方面,由于寡头发电企业抬高了市场出清价格,其余发电企业在“搭便车”的情况下均获得较高的市场利润率。市场垄断情况越严重,发电企业“搭便车”收益增幅越大,待建机组补贴率越高。
图8 给出了垄断竞争环境下发电企业在不同方案中的容量市场中标情况。可以看出,寡头发电企业的策略性报价行为导致该主体在容量市场中的出清率大幅减少。以发电企业Ⅰ为例,出清率由方案3 的72.87%逐步下降至方案5 的55.15%。可见,寡头主体通过牺牲其在容量市场的出清率来提升自身的市场垄断地位,即主体垄断效果越明显,该主体市场中标率越低。相反地,非寡头主体由于占有的市场份额较少,在4 个方案中仍按机组缺额成本进行报价,机组出清率变化较少,机组中标率基本维持在80%以上。
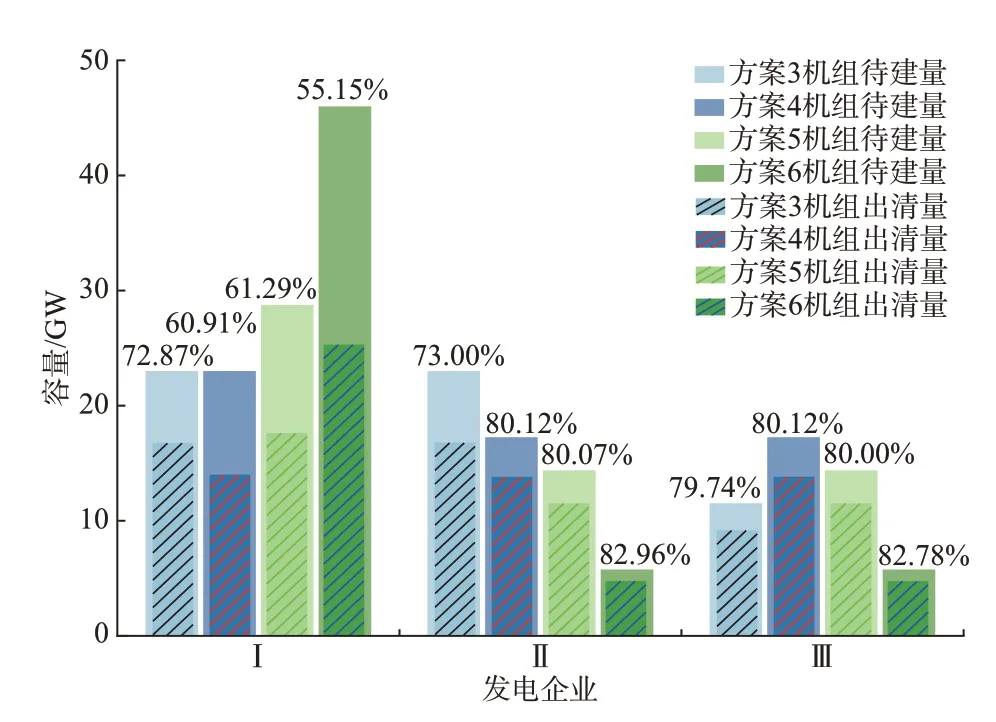
图8 垄断竞争环境下发电企业在不同方案的容量市场中标情况对比Fig.8 Comparison of bidding winning situations of power generation enterprises in capacity market with different schemes under monopolistic competitive environment
5 结语
本文为分析发电企业参与容量市场博弈竞价行为,提出了一个多领导者纳什-主从博弈模型。为拓展所提出博弈模型的求解空间,本文采用共享约束方法对模型进行修改,并利用KKT 最优性原理将模型转化为广义纳什均衡模型,然后通过构造势函数将模型重构成势博弈模型。本文采用中国某省实际数据进行仿真,验证了所提出博弈模型的有效性。算例结果表明,容量市场中发电企业的高额市场存量机组占比将容易增强该市场主体的市场力,导致发电企业采取策略性报价行为,抬高其在市场中的容量报价,造成出清价格上涨,用户容量成本增加,机组补贴容量比例降低。本文为容量市场设计者提供了模拟市场运行结果与评价市场运作效果的工具。容量市场设计者可以模拟发电企业参与容量市场博弈竞价的问题并且获取市场的出清情况,从而分析寡头市场主体的影响程度,进而对容量市场运作规则进行相应修改。
本文下层模型仅考虑容量市场的出清问题,忽略了不同市场间的协同、耦合运行问题。伴随着新型电力系统建设的逐步推进,新能源装机容量占比将持续上升。为充分消纳具有高波动性、随机性的新能源,系统需要大量的灵活性资源。此外,随着中国碳排放权交易市场建设的逐步完善,碳配额的免费发放比例逐步收紧,具有较低碳排放强度的发电机组将具备较大竞争优势。低碳排放强度机组与高灵活性机组将在容量市场中拥有更大的竞争潜力。后续研究将进一步考虑容量市场与碳排放权交易市场、现货市场、绿电交易市场之间的耦合关系,分析发电企业参与多能源市场的博弈竞价行为,探索市场耦合对于不同风险收益偏好发电企业设定待建机组单位容量缺额成本的影响。
