元认知视角下物理习题课的教学追求

朱加沐

［摘 要］习题课教学不仅承载着唤醒学生对知识的记忆、知识体系的重构等认知活动，更是学生对解题思维过程的再认知过程。因此，学生在习题课上不仅要考虑解法的优劣性和过程分析的合理性，还要监控自己的解题过程，调控自己的注意力，评估解法，总结反思等。文章探讨了习题教学中，学生借助元认知对自己的解题过程进行自我调整的方法。

［关键词］元认知；习题课；科学思维

［中图分类号］    G633.7        ［文献标识码］    A        ［文章编号］    1674-6058（2023）14-0053-03

与传统高考相比，新高考的试题更加灵活，这就要求课堂教学要以学生为中心，关注学生的个性发展。长久以来，习题课尤其是高三复习课气氛沉闷，学生缺乏学习的激情和热情，缺少了深度思考的课堂学生缺乏获得感。此外，习题课的教学目的之一是教会学生学习，而学会学习很大部分源自学习策略的获得与调整，包括学生会用什么策略来理解试题的意图，怎样获得有效的证据支持自己的观点，怎样自建理论有效地进行解释，等等。在实际教学中，让学生学会元认知思考，借助元认知策略，可有效提高习题课教学效率。

一、元认知理论要义解读

元认知的研究者弗拉维尔（Flavell）将元认知定义为，个体对自己认知状态和过程的意识和调节，即对认知的认知［1］。元认知是学生对自己认知发展水平的客观认识情况，在内容上多数学者认为可以包括元认知知识、元认知体验和元认知监控三个部分［2］。

习题课元认知教学，包括：（1）习题课元认知知识，是指学生对影响习题认知过程和结果的那些因素的认识，是经过一定量的习题教学之后累积起来的关于认知活动的影响因素及其影响方式的一些知识，对调整、反思起着关键性作用。（2）习题课元认知体验，是指学生对问题的表述而产生的理性和感性的综合体验，主要有问题的难易度、熟悉度、相似度、抽象度、障碍度、达成度、困惑度、成就感等。（3）习题课元认知监控，是学生学习过程中对习题课教学整个过程的计划、控制与调整，包括学生明确题意、回忆相关知识、选择解题策略，确定思路，检查错误，优化思路，小结收获，纠正错误，排除障碍，调整思维等［3］。

二、元认知视角下习题课教学的策略

［引入相似情境，让学生充分表达］

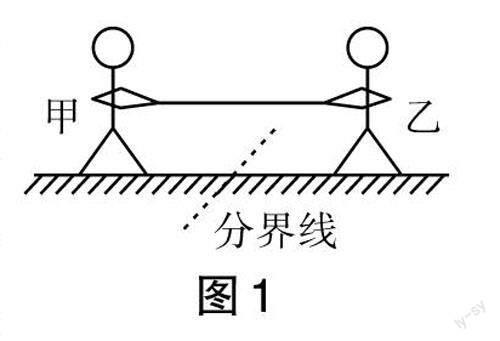
［例1］如图1所示，甲、乙两人在冰面上“拔河”，两人中间位置处有一分界线，约定先使对方过分界线者为赢。若绳子质量不计，冰面光滑，则下列说法正确的是（）。

A.甲对绳的拉力与绳对甲的拉力是一对平衡力

B.甲对绳的拉力与乙对绳的拉力是对作用力与反作用力

C.若甲的质量比乙大，则甲能赢得“拔河”比赛的胜利

D.若乙收绳的速度比甲快，则乙能赢得“拔河”比赛的胜利

在学习牛顿第三定律时解决过拔河问题。对于本题，学生第一直觉就是搜索两种拔河比赛的相似之处——“拔河”，从而进入到自认为“熟悉”的情境中，因此错误地认为与本题相匹配的要素只有作用力与反作用力。可学生还是会想当然地认为：质量大，最大静摩擦力大，拔河容易胜。但殊不知两种拔河情境的差异在于，粗糙地面和光滑的冰面上“拔河”是不同的。为此，教师可以引导学生认知自我，思考：“正常的拔河，靠什么能赢？怎样表明赢了？”“光滑的冰面上拔河没有了摩擦力，是不是也是一方不动，另一方被拉过来？”“约定先使对方过分界线者为赢是什么意思？能否转换成物理量？”“怎么推算运动到中点的时间？”

学生的表达不仅要有科学内涵，还应有社会内涵。科学内涵应当提供论据以支持论点；社会内涵应当把自己作为特定类型的人来对待（如有道德的，诚信的，感性的等），学生易停留在社会内涵的层面上。但平时的感性体验易造成情境的似是而非，因而容易產生混淆。如果物理教师和其他学生总是以科学的内涵对待试题，对不同表述做出反应，能让学生自行找异同、提问题的话，就有助于学生把反应与原来展示科学论点的情境相联系，增加试题情境的识别度，久而久之，学生的思维能力就会得到提升。

［合理设问，谨防思维定式］

［例2］如图2所示，质量为M的木板上表面水平，放在水平桌面上，木板上面有一质量为m的物块，刚开始均静止。物块与木板及木板与桌面间的动摩擦因数均为[μ]，若要以水平外力[F]将木板抽出，则力[F]的大小至少为（设最大静摩擦力与滑动摩擦力大小相等）（）。

A. [μmg]                    B. [μ（M+2m）g]

C. [μ（m+2M）g]    D. [2μ（M+m）g]

学生错误地认为木板所受的外力[F=f1+f2] ，[F]的方向向右，如图3所示。可以引导学生这样认知：“如果真是这样，分析物体受力会发现向左的摩擦力分别为[f1]和[f2]，且[F'1=f1+f2]，[F'1]对物体的作用效果怎样？”“可以看到怎样的现象？”“何谓抽出呢？对应着哪些物理量？”“我们的思路要做怎样的调整？”

现代学习观认为，学生有时会利用已获得的碎片化知识断章取义地理解或解读新知识，但事实上是大部分学生必须通过大量的事实性知识和相应训练，才能有效地向新情境迁移。因此，如果利用物理中的一些二级结论或者熟记一些常见的模型，一方面会影响学生对周围环境的关注，还会影响学生对相关问题素材的组织和解释，在条件不变的情况下有利于学生快速解题；另一方面，也会使学生的学习过程变得僵化，会影响思维量较高问题的正确答题，也不利于学生推理能力以及获取、更新知识能力的提升。习题课教学中，教师应引导学生设置问题，并参与分析、破除思维定式。

［展示学生错误，分析归纳错因］

［例3］如图4所示，质量[m=2 kg]的物体静止在水平地面上，物体与水平面间的滑动摩擦力大小等于它们间弹力的0.25倍，现对物体施加一个大小为[8 N]、与水平方向成[θ=37°]角斜向上的拉力[F]，已知[sin37°=0.6]，[cos37°=0.8]，[g]取10 m/s2。求：

（1）物体在拉力作用下5 s末的速度大小；

（2）若5 s末撤去[F]，求再经过3 s的速度大小。

归类展示学生错误。

解析：（1）[f=μmg=5 N]（错一），

[f=μFN=μ（mg-Fsinθ）=3.8 N]，[ma=Fcosθ-f] ，解得[a=1.3 m/s2] ，[v5=6.5 m/s] 。

（2）撤去[F]后，物体做匀减速直线运动，[v8=v5+at=6.5+（-1.3）×3=2.6 m/s2]（错二），

撤去[F]后，[a2=fm=1.9 m/s2]（错三），

撤去F后的受力分析有[f=μFN=μmg=5 N]，[ma2=f]，[a2=2.5m/s2]。

[v8=v5+at=6.5+（-2.5）×3=-1m/s2]，负号表示运动方向相反。（错四）

刹车问题：[t停=Δv-a2=2.6 s<3 s] ，已停止，再经过3 s的速度为零。

心理学研究表明，具体类型的教学可以使人们有选择地感知输入，进而完成适应性任务［4］。错题归类教学能够功能性地重组人脑中原有的碎片化知识，并有效利用。知识只有在能够被应用或被批评的时候才具有价值，而要改变学生的逻辑错误，需要大量的证据与之进行“对质”，因此，适当安排一些反例、重组问题或者典型错误的再认知过程，能让学生主动地思考自己或同学的解法特征与某些特定概念的关联度，有助于学生关注试题中知识或者能力的新特征。

［分析试题情境，巧用图像辅助］

［例4］将自行车转弯近似看成绕某个定点[O]（图中未画出）做圆周运动。如图5所示为自行车转弯过程中某时刻的俯视图，[A]点、[B]点分别为自行车前、后轮轴中心上的点，虚线表示前、后轮转弯的轨迹，则[A]点和[B]点的（）。

A.线速度相同

B.角速度相同

C.向心加速度相同

D.线速度、角速度和向心加速度都不同

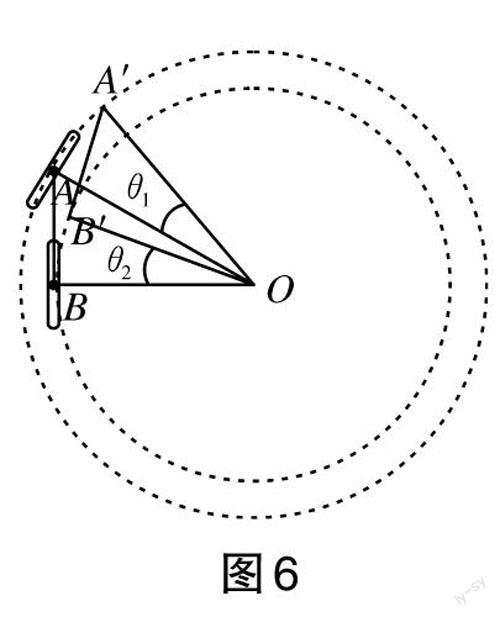
本题是2021届上海宝山区高三二模的一道选择题，改编自2013年上海嘉定区一模的填空题。相对原题而言，本题较为简单，可是学生错误率较高。答案仅仅给出A、B两点同时绕着O点转动，所以具有相同的角速度，故B选项正确，但是学生还是一片茫然。学生的问题在于不能从题设的图像读出完整的物理信息。教学中，教师可以引导学生认知：自行车绕某个定点O（图中未画出）做圆周运动，能不能定出圆心和画出两个轮子的圆轨迹？怎么确定圆心？前后轮的方向能说明什么？如果圆心确定了能否建立了如图6所示的圆周运动的模型，描述圆周运动线速率或者角速度？同轴转动模型中的两点为什么角速度相等呢？本质是什么？本题还可以设置关于两个物体的哪些问题？（如几何方面的，运动方面的）

物理学科核心素养中的科学思维（包括了模型建构），常需要学生自己建构模型，把生活中的复杂情形理想化、进行物理抽象，从而使问题简化，以便分析理解，进而有利于抓住物理现象的本质。模型的建构需要学生不断调整题设信息，有效调动理解过程中的知识关联，而借助图像、图示等工具，可使学生对物理问题的分析与重构更高效、更靠近物理知识的本源，但前提是，学生要知道自己会遇到什么样的困难，因此要注重发展学生的自我提问能力。

三、元认知视角下习题课的教学追求

新知识的建构必须始于已有知识，对这一教学观的合理引申就是需要关注学生的原有知识及可能的问题，如在给定学习主题时，随之而来的可能有对主题的不完整理解、错误观念和对概念的天真解释［5］。在习题课教学前，尤其是高三复习阶段，学生已具备了一定的前概念，但还需要依据这些概念帮助学生对相关物理知识达到更加成熟的理解，从而有效培养学生的思维能力。高中物理习题课中，教师应有意识地引导学生调控自己的解题过程，发展学生的元认知能力，尤其是要发展学生的习题课元认知监控能力，而不应让学生驻留在习题课元认知体验这一层面。

初期，教师可以提问学生“你是如何思考的？”“你是怎么做到的？”等。后期，可以要求學生以自我提问的方式澄清自己的选择，如“我是怎么知道的？我怎么决定？为什么我这么认为？这种做法错误的原因是什么？这种情境怎么建立模型并转变为物理量？”由提问转化成反问，由个人学转变为同伴学，从而解决问题。因为问题解决是一种积极的应对策略，教师引导学生认识到自己的解法问题所在，一方面可以提高学生的学习积极性，另一方面可以提高学生自我检查、评估、修正的能力，并把这种能力运用到新的情境中，发展学生的核心素养，并使之迁移到今后的学习生活中。

借助元认知策略，创设合适的场景，让学生发现自己所面临的问题，反思解法，讨论错误概念，这样更加有利于学生深度思考，激发学生的学习热情。习题课教学的元认知策略，本质上是学生的自我意识和自我调整，但归根结底是以提升学生的科学思维能力，发展学生的物理素养为追求。

［   参   考   文   献   ］

［1］  孙旭炜，肖洋，熊建文，等.物理实验元认知的含义、内部关系模型与作用机制［J］.物理教师，2015（6）：2-7.

［2］  王坤. 网络环境下促进阅读元认知的策略研究［D］.保定：河北大学，2008.

［3］  姜乐，赵景春.物理教学过程中发展学生的元认知技能［J］.网络财富，2009（2）：119-121.

［4］  贾冠杰.认知神经科学与双脑外语教育模式［J］.外语与外语教学，2006（12）：20-22，66.

［5］  贲友林.将学习科学应用于课堂教学实践：读《人是如何学习的：大脑、心理、经验及学校》［J］.江苏教育，2013（Z1）：125-126.

［6］  张英豪，王友，朱光亮.物理试题分类精选、解析及误区警示（上）［J］.试题与研究，2011（22）：50-72.

［7］  徐飞翔.借用板块模型构建变式，培养物理思维能力［J］.高中数理化，2016（16）：28.

（责任编辑 易志毅）