基于磁链观测器的ROV 无传感器推进控制研究*

徐大勇 魏海峰 王浩陈

（1.海军装备部驻南京地区第一军事代表室 210006）（2.江苏科技大学自动化学院 镇江 212100）

1 引言

集成推进是一种新型的电力推进装置，它将电机转子和螺旋桨叶片集成在一起，消除了推进轴系统。它具有结构紧凑、功率密度高、效率高、振动低、噪声小等优点。由于集成度高、结构复杂，给一体化电机推进装置的设计和制造带来了困难。一体化电机推进具有低噪声的特点，适用于水下安静航行器［1～3］。传统的永磁同步电机多采用矢量控制策略，需要准确的转子位置信息来实现速度和电流控制。位置传感器通常是一个旋转变压器或编码器。由于一体化推进电机无轴，传统的机械位置传感器安装困难［4～5］。因此，多采用无位置传感器控制，有利于简化驱动器与螺旋桨之间的布线，提高抗电磁干扰能力，提高系统的整体可靠性［6］。

在文献［7］中提出的非线性永磁同步电机模型的观测器中，使用锁相环方法估计转子角速度。该方法具有估计误差为零的局部收敛性，并且难以显示闭环系统的稳定性。有学者提出带一种补偿校正的改进反电势观测器，保证观测器在零速和低速时的有效性［8～9］。永磁磁链在运行中相比电阻、电感有着更加稳定的特性，以磁链为基础观测器得到研究人员的关注。文献［10］提出一种利用磁链误差的改进滑模观测器，提高无传感器控制的转速位置观测精度及运行抗干扰能力。也有学者利用全阶的磁链观测器作为模型参考对象，实现对控制对象的更优控制［11～12］。

本文提出了一种自适应外部负载的改进观测器，其估计误差在有限时间内全局收敛到零。其分两步构造。在第一步中，设计了一种磁链和位置估计算法。在第二步中，使用位置估计获得转子角速度和负载转矩的观测器。并对改进观测器和传统观测器进行实验对比。

2 永磁同步电机模型

采用经典的αβ两相静止坐标系下的永磁同步电机模型为

其中，λ为磁链；i是αβ轴电流矢量；u是αβ轴的电压矢量；L、R分别为定子绕组的电感和电阻；J为转子转动惯量；θ为转子机械角度；ω为机械角速度，np为极对数，τL为负载转矩；λm为本体永磁磁链；

唯一测量的信号是定子绕组电流和电压。除了极对数、定子绕组电阻和电感之外，电机参数被认为是未知的。假设外部负载是恒定的，且不考虑摩擦。

目标是设计使用电流和电压测量值的观测器，并在有限时间内提供磁通量、角位置、速度和负载扭矩的估计值，例如，当时间t≥t1以下条件成立：

其中，、、和τL(t)分别为估算的磁链、转子角度、负载、转子角度。

3 改进磁链观测器

3.1 磁链和转子位置观测

根据式（1），首先定义一个映射φ(x)：

则有逆映射关系：

对式（3）的求导有：

验证式（3）和（5）的系统的线性回归方程为φT(t，α)χ=c(t，α)。其中，φ(t，α)，c(t，α)均是可计算的：

其中：

根据动态回归扩展和混合方法［4］，采用了两个线性滤波器，其传递函数为，其中=αi＞0，i=1，2。并获得扩展回归模型：

在动态回归扩展和混合方法的下一个“混合”步骤中，分解原始线性回归模型（6）转化为标量方程组：

其中：Yx(t):=adj{Φ(t)}C(t)，Δ(t):=χdet{Φ(t)}

从式（4）、（5）和（7）可获得磁链观测器方程：

其中，γx为自适应增益（γx＞0），为估算的磁链。

应用到文献［6］中，可得到有限时间的磁链估计：

其中，函数wλ计算为且有ρλ∈(0，1)，w1=-γλΔ2。w1是具有初始条件w1(0)=1，的可计算信号。如果以下条件成立，所述改进可确保估计误差在有限时间内全局收敛到零：

使用式（9）的磁链估计，可在有限时间内估算除转子位置：

3.2 角速度和负载转矩观测

通过使用上述式（11）中获得的转子位置估算值，再迭代的方法来设计转子速度和负载转矩的观测器。从式（1）中，可导出方程组：

其中：

对式（13）采用动态回归扩展和混合方法，推导出标量回归和计算出负载扭矩和速度的估计方法：

其中，Z=adj(Q)z，Δq=det(Q)，γm，γτL＞0 是自适应增益，和分别是速度和负载转矩的估计值。

进一步，采用与式（9）类似的修正方法［6］来估计有限时间内的负载转矩：

且有ρτL∈(0，1)和=-γτLΔ2q，w3是可计算的信号，其初始值w3(0)=1。

在最后一步中，结合式（14）、（15）和相同修正方法［6］，得到有限时间的速度估计：

其中：

且有ρw∈(0，1)和=-γwΔ2q，w4是可计算的信号，其初始值w4(0)=1。

可以看出，与式（9）的式（10）类似，存在tτL，tλ之后，在没有测量噪声的情况下，角速度和负载转矩的估计误差等于零。因此∃t1:t1≥tλ，t1≥tτL，t1≥tω，t1≥tθ，且满足所需条件（2）。

4 实验结果与分析

选取参考转速600rpm，是区间中的中间值，两种方法的占比都是50%。仿真参数设定：电机D 轴电感12.2mH，Q 轴电感15.4mH；定子电阻0.035Ω，磁链0.065Wb；阻尼系数取0.009 N·m/(r·min-1)，转动惯量取0.0003 kg·m2。仿真结果如图1、2 所示。

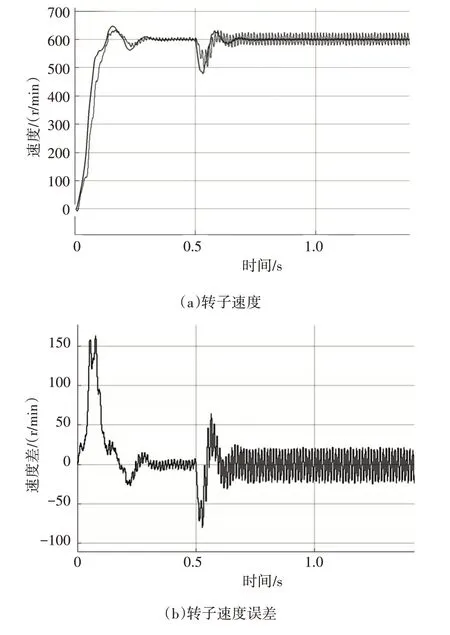
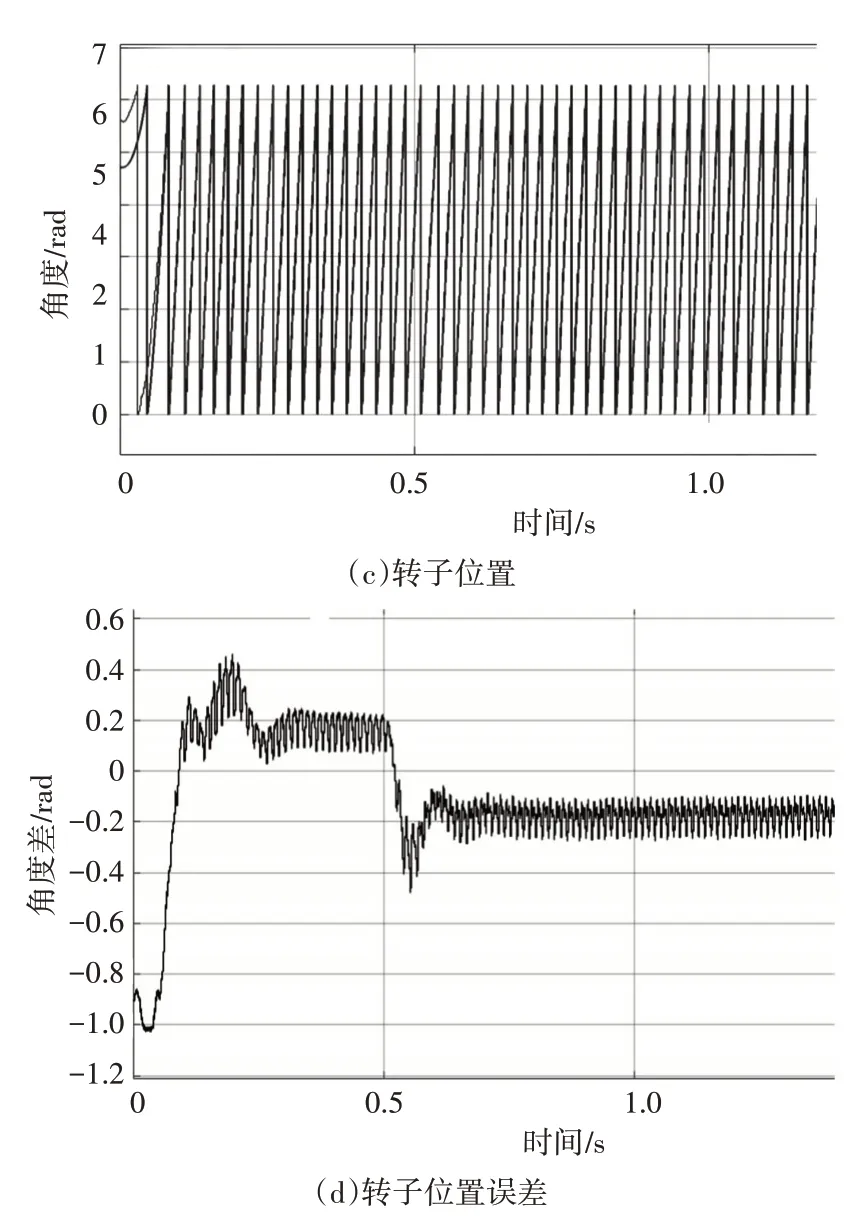
图1 基于传统磁链观测器的仿真结果

对比图1 与图2 结果可知，本文改进磁链观测器的观测精度要优于传统的观测算法。传统磁链观测器估算出的角度误差较大，其误差无法收敛至0，而改进算法能够在有限的时间内将误差收敛至0 附近。尤其在速度跟踪响应上，改进算法要明显优于传统算法，其实际转速和估算转速几乎一致。且在600r/min的低速控制中，有着较好的稳态效果。

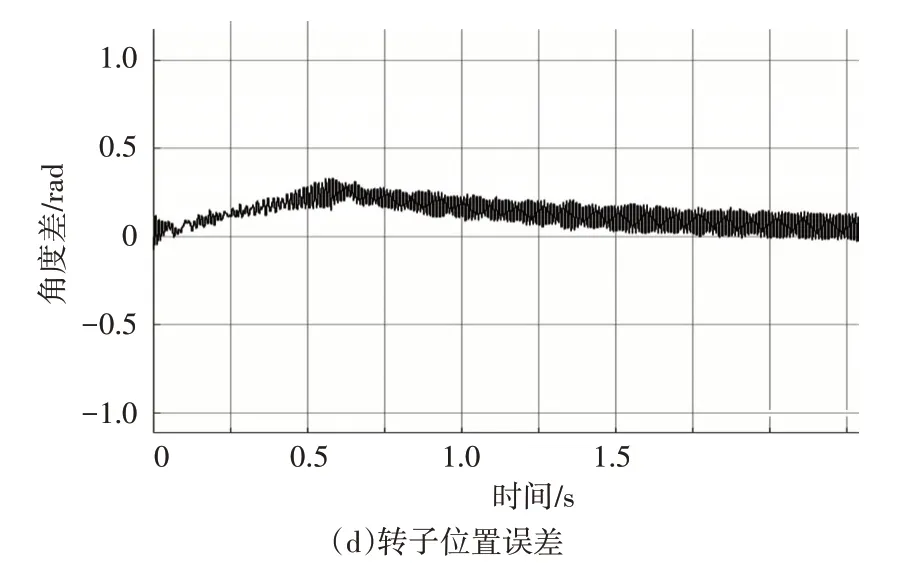
图2 基于本文改进磁链观测器的仿真结果

5 结语

本文构建了永磁同步电机磁链、角位置和速度的自适应观测器。在没有测量噪声的情况下，估计误差在有限时间内收敛到零。通过迭代应用该方法构造观测器。通过实验证明，改进磁链观测器的估算精度要高于传统磁链观测器算法，且响应迅速。