基于SW-DBA-DCNN 的滚动轴承故障诊断方法*
2023-08-30张恒佘博王俊王旋
张 恒 佘 博 王 俊 王 旋
(海军工程大学兵器工程学院 武汉 430033)
1 引言
长期以来,轴承等工业领域核心机械部件普遍经受着载荷冲击复杂、强烈、高转速工况持续时间长、强噪声干扰等问题的考验[1],一旦其不堪重负,这些隐患将严重影响到人员和装备的安全。目前基于数据驱动[1~4]的故障诊断是装备健康管理领域的研究重点,由于深度学习具有深层结构和较强的非线性特征提取能力[5~6],面对复杂工况[7]条件下的故障诊断研究需求也更为贴合,目前的深度学习网络模型有卷积神经网络、深度置信网络、循环神经网络、堆叠自动编码器等。
这些方法目前已经在故障诊断领域得到广泛的应用[8~9],但存在的问题之一是在故障诊断的实际应用中数据样本量差异较大,给正确进行故障诊断带来了困难。Li[10]等提出了7 种数据扩增的方法,有效验证了时间序列扩增的可行性。Kun[11]等在提出5 种数据扩增方法的基础上分析出基于时间序列的信号转换和时间拉伸技术能够取得较好的扩增效果。
为应对上述数据样本量不平衡的问题,通过引入滑动窗口(Sliding Window,SW)、动态时间规整(Dynamic Time Warping,DTW)[12]思想,结合深度神经网络,本文提出一种基于SW-DBA-DCNN 的滚动轴承故障诊断方法。首先,提出一种基于SW-DBA的数据扩增方法,实现非平衡样本的数据扩增[13]。其次,构建一个以深度卷积神经网络(Dynamic Convolution Neural Network,DCNN)为基础的网络模型并确定其模块组成、输入输出和数据结构。最后,通过设置数据扩增前后对比实验,验证所提方法的有效性。
2 传统数据扩增方法
2.1 基于SW的数据扩增方法
Sliding Window(SW)方法是一种在给定窗口大小的数组或字符串上提取子元素问题的方法,可以将提取子元素时的嵌套循环转换为一个循环,大大降低算法的时间复杂度。该方法的工作理念在深度学习的应用中极为广泛,特别是卷积核在卷积层、池化层中的滑动,能够让卷积核遍历所有数据,实现数据量的成倍增加。类似地,在时间序列信号中定义一个固定步长和长度的窗口,该窗口的长度和步长的乘积远大于原始数据量,也可以达到扩增数据量的目的。
如图1,图中设置了一个滑动步长s为80,窗口大小l为200 的滑动窗口,这个窗口可以将一段信号长度L为1200 的数据划分为x段长度为l的数据。
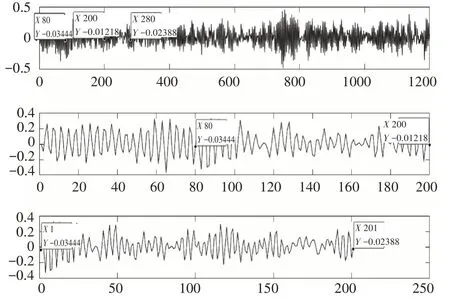
图1 滑动窗口(SW)原理示意

图2 SW-DBA计算流程
2.2 传统DTW的数据扩增方法
Dynamic Time Warping(DWT)所处理的对象的是时间序列数据,其基本原理就是度量两个时间序列Xi,Yj(其中i≠j)的相似性,通过把时间序列信号局部拉伸或者压缩,使其相似点能够尽可能地对齐。
序列之间的相似性是由相似点间的距离来衡量的,而DWT 所使用的方法就是将这些所有相似点[xi],[yi] 之间的距离加和得到总距离(Warp Path Distance),距离越小则相似度越高,以此来衡量两个序列之间的相似性。具体过程如下:
1)定义两个序列A和B,一个距离矩阵C[m*n],矩阵里的元素(i,j)表示Ai和Bj两个相似点间的距离D(Ai,Bj),lk=(i,j)k表示路径L的第k个元素。
L=l1,l2,l3,...,lk-1,lk
(max(m,n)≤k<m+n-1)
2)为了保证这条路径不是随意选择的,每一个路径节点的确定还需要满足单调性和连续性的条件,因此,该路径的当前点是l(i,j)时,那么下一个路径节点就只能是l(i,j+1),l(i+1,j),l(i+1,j+1)中的一种。
3)这样看来,符合上述条件的路径可能有很多个,而现实需要的是变换代价最小的路径DTW(A,B),即:
每次计算的距离都是前面距离的累加,累计距离表示为
4)常规方法在找到最优路径后,对该路径进行线性拟合,在线性拟合时需要设置每个路径节点的置信因子,得到不同置信水平下的多条路径,进而可以获得更多的新增数据。
2.3 基于动态时间规整(DTW)的全局平均Dynamic Time Warping Barycentric Averaging(DBA)方法理念
首先,与DTW 不同的是DBA 的数据扩增方法是一种基于DTW 动态时间规整的全局平均方法,它会初始化定义一个平均序列,通过迭代计算不同时间序列对于平均序列的DTW 全局平均值,反复完善最初的平均序列,以最小化其与平均序列的平方距离(DTW)之和。
实际上平方总和的最小化问题就是平均序列的每个坐标的部分和的最小化问题。由于一个序列集至少含有两个序列,平方总和是一个多序列平方和的总和,通常被称为组内平方和(Within Group Sum of Squares)。这里需要注意的是,平均序列的共同坐标的形成都是由每一个其他序列的一个或者多个相似点的贡献的,那么取这组相似点坐标的重心(Barycenter)就能实现对该平均序列坐标贡献的量化。
具体实践上,DBA的计算分两个步骤:
1)在创建的序列集中,每个属于这个序列集的单独序列都要和正在完善的临时平均序列计算DTW,找到平均序列的坐标和序列集的坐标之间的联系。
2)对平均序列的每个坐标进行迭代更新,每一次迭代更新的值即为第一步中与之相关的其他单独序列坐标的barycenter,直到迭代收敛。
(1)定义S={S1,S2,...,SN}为待平均化处理的序列的集合;T=<T1,T2,...,TK>为迭代第i次的平均序列;为第i+1次迭代的平均序列,即对第i次迭代后平均序列的更新。这些序列的坐标都被定义在一个任意的欧式矢量空间E中。
∀k∈[1,K],Tk∈E
(2)运用函数assoc 将平均序列的每个坐标与S中的一个或者多个序列的坐标联系起来。这个函数是在计算T和S的每个序列的DTW 期间计算的。然后,平均序列T'中的每一个坐标kth就可以被定义为
T'=barycenter(assoc(Tk))
其中:
(3)另外,平均序列T(K)还必须满足以下条件:
(4)再次计算平均序列和的所有序列之间的DTW,进行迭代,直至其收敛。
3 基于SW-DBA-DCNN 的滚动轴承故障诊断模型
本文在SW、DTW 两种传统数据扩增方法基础上,将两种方法相融合,并引入DBA 的计算理念,扩增出新的数据用于深度卷积神经网络的训练,以此来解决输入数据量少、样本不平衡的问题。
3.1 基于SW-DBA的改进数据扩增方法
基于SW-DBA的扩增方法,具体流程如图3。

图3 DBA计算结果
1)假设某工况下轴承损伤实验原始数据样本量较少,需要进行数据扩增,将该数据进行下采样,规整数据长度。
2)设计滑动窗口的步长,窗口宽度,滑动次数,通过对某一信号进行滑动窗口读取,得到固定长度的信号。
3)将生成的信号组分解成每两个信号为一组的信号组。
4)以DTW 相似度作为评判标准,通过调用DBA算法对信号的全局时间序列动态求平均,所求的平均结果即为新信号的时间序列值,将输出后的平均序列看作是新增的信号。
5)依次对信号组中的相邻两段信号求平均,即可实现多段信号的新增。
经过SW 处理后的两组数据作DBA 计算,得到平均序列如图3中第三条曲线所示。
3.2 基于改进数据扩增方法的滚动轴承故障诊断模型
首先,将原始不平衡的数据进行FFT 预处理,这样,样本就由时域转变为频域,每个样本的维度由1024 变为512。其次,长度为1024 的原始数据经由SW-DBA 处理后,产生x(根据达到数据平衡的实际需求调整)个与原始数据长度相同的新增序列,这些新增序列再通过FFT 处理,得到相同数量的具有512 个傅里叶系数的向量。最后,将FFT 变换后的新增序列作为原始数据的补充一起输入到DCNN进行训练。
本文的一维深度卷积神经网络共设置五层卷积、池化,1 个全链接,输出采用SoftMax 分类,具体的网络数据结构和超参数设置见表1。首先分别定义卷积层输入的批次、高度、宽度、通道,以及卷积核的大小、滑动步长、填充方式。另外,选用最大池化层,分别设置最大池化窗口的大小,水平、垂直滑动步长。为了防止训练过程中出现梯度消失或梯度崩塌等情况,通过在卷积层和最大池化层之间设置BN 层。在训练的循环中,每一层的训练都会改变一次权重,待五层网络训练结束后,损失函数经过反向传播又会再一次更新各层的权重,

表1 DCNN数据结构和超参数设置
直到得到损失函数极值或者已经提前达到预先设定的训练次数,具体计算流程见图4。

图4 SW-DBA-DCNN计算流程
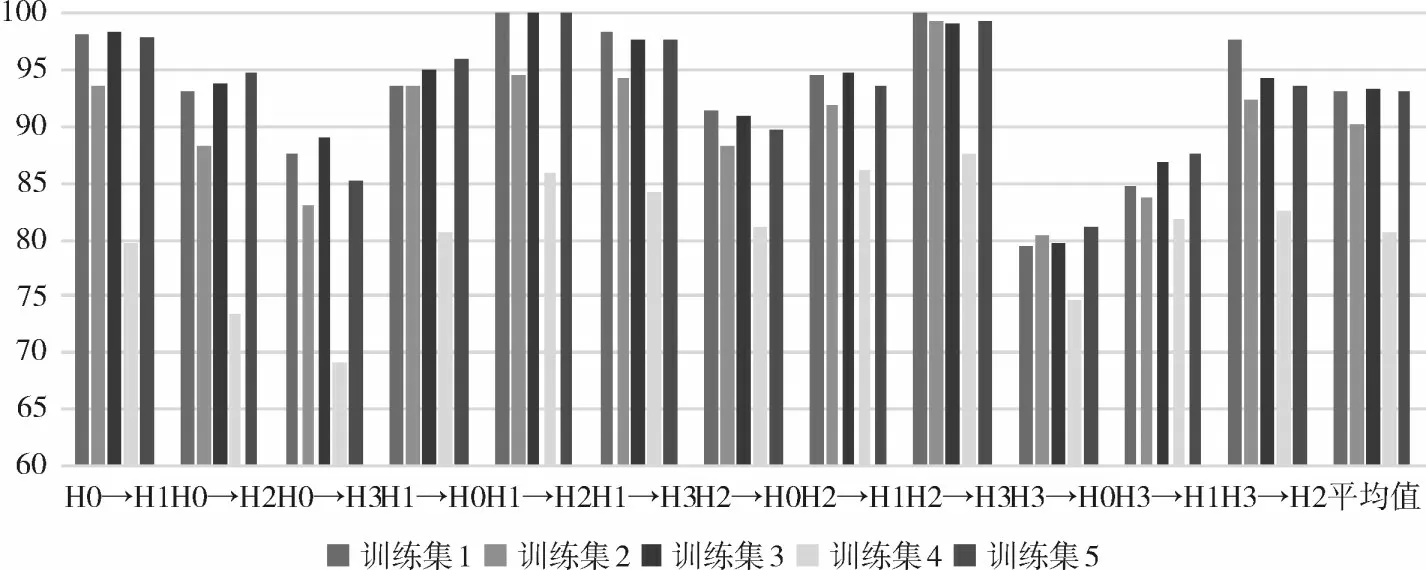
图5 变工况条件下不同数据集数据扩增前后准确率对比
4 滚动轴承故障诊断实验验证及分析
4.1 数据集说明
本实验采用的数据集为凯斯西储大学的公开数据集,该数据集提供了轴承的不同损伤部位,不同损伤程度,不同采样频率等较为完备的实验室条件下的数据。为了模拟样本量不平衡的情况,本次实验在源域数据的选择时采用轴承端10 种故障类型的不同数据,其中外圈故障统一选择6 点钟方向故障。
4.2 实验设置
本实验人为地设置每种故障状态下的数据量,致使十种故障的样本数据量不平衡,具体数据量设置如表2。
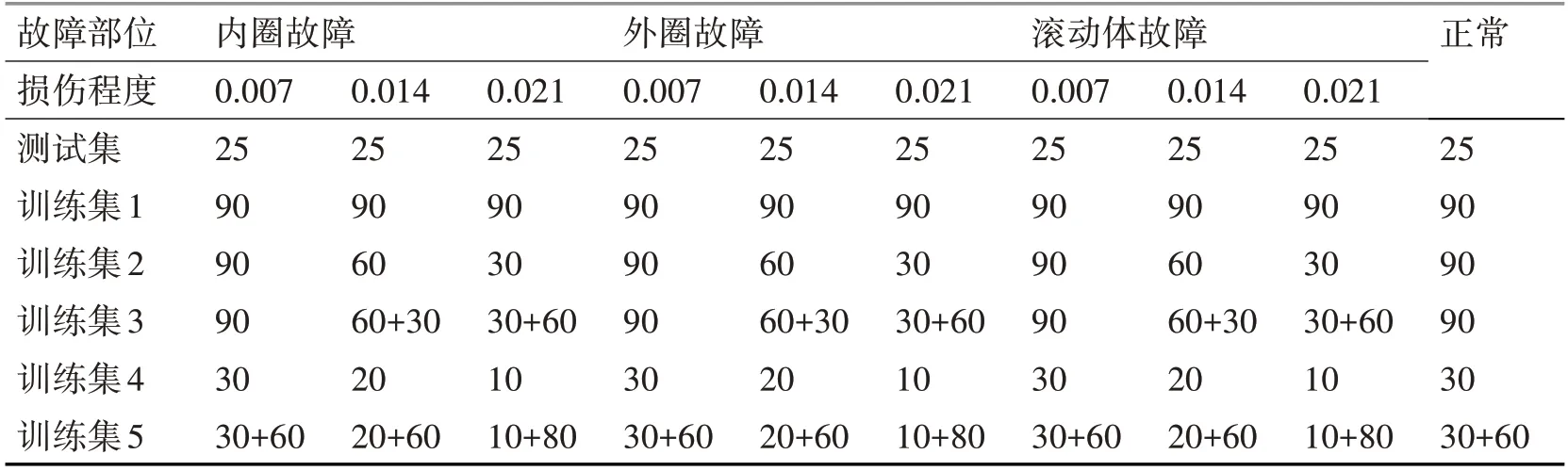
表2 训练样本输入组数设置
其中训练集1 是平衡样本,训练集2 和训练集4 是非平衡样本,训练集3 和训练集5 是采用SW-DBA 算法,分别在训练集2 和训练集4 的基础上将所有非平衡数据样本扩增至90 组,得到的平衡样本数据。需要注意的是,这里设置的扩增后每种故障类型的数据组数为90 组,指的是在原本已有样本的数量基础上补齐90 组数据,而不是直接新增90组数据。
另外,本文设置的对比实验严格控制变量,对比实验使用的是同一个测试集,变工况种类相同,保证了只有源域数据的数据量的差异而不存在其他差异,较为真实地模拟了针对训练样本不足问题实施数据扩增的效果。
4.3 准确率分析
通过对比两次实验变工况条件下故障准确率,可以分析得出:
1)表3展示了0,1,2,3四种负载排列组合产生的12 种变工况条件下不同训练集的故障诊断准确率,可以看到,相较于训练集2,扩增后的训练集3仅在H2-H3、H3-H0 工况下准确率略低于训练集2,其他变工况的准确率均有所提升;训练集5 的准确率则在各种变工况条件下全方面超越了训练集4。

表3 变工况条件下不同数据集数据扩增前后准确率对比
2)在训练样本缺失较少的训练集2和训练集3的对比实验中,使用本文所提方法可有效提升各工况条件下故障诊断准确率水平,将DCNN 模型的平均故障诊断准确率提升了3.02%;
3)在训练样本缺失较大的训练集4和训练集5的对比实验中,扩增后的数据使得故障诊断的平均准确率大幅提高了12.47%。
4)扩增到同样数据组数后的训练集3 和训练集5 的准确率结果也基本持平,能够达到训练集1平衡数据组数条件下的准确率水平。
综上,SW-DBA的数据扩增方法对于非平衡样本的准确率提升效果显著,在很大程度上解决了现实应用中训练样本不平衡的问题。
5 结语
针对数据样本量的不平衡问题,本文首先构建了一个深度卷积神经网络模型,提出一种SW-DBA的数据扩增方法,通过模拟设置两组样本不平衡、一组样本平衡、两组数据扩增后平衡的对比实验,得到结论如下:
1)本文提出的SW-DBA 方法能够对有限的非平衡数据进行扩增,增加样本的输入量,有效解决了数据样本的非平衡输入问题。
2)利用西储大学数据集,本文构建的SWDBA-DCNN 故障诊断模型能都出色地使用新增数据进行故障诊断,对非平衡样本在不同变工况条件下故障准确率都有所提升。验证了该方法的可行性和有效性,可以解决滚动轴承故障诊断领域样本数量不平衡的问题。
