基于应力强度干涉模型的雷达机械设备重要度分析*

王雨辰 权怀炜

（1.导航技术研究所 西安 710068）（2.西安航天天绘数据技术有限公司 西安 710068）

1 引言

20 世纪50 年代，可靠性学科产生，随着该理论的普及，越来越多人关注到可靠性理论在实际工程中发挥的重要作用。而机械设备作为一种基础设备，在多种大型系统中发挥作用，包括基建工程，船舶工程，雷达设备等。雷达系统的许多设备组成都是由各类机械设备组成，如天线座主体，传动部分，驱动部分，方位和俯仰部位的铸件等［1］。

系统可靠性理论从通用质量特性的角度出发，旨在降低系统失效概率并识别出系统中的薄弱环节，从设计之初提高雷达机械设备的可靠性水平，其中，重要度理论在其中发挥着重要作用。因此，针对雷达机械设备的重要度分析，可建立适用于机械设备的可靠性模型，并在这个基础上获取机械设备的重要度模型，从而将雷达机械设备的重要度分析应用于实际工程中，从而提高雷达机械设备的通用质量特性［2］。

2 Birnbaum重要度

Birnbaum 重要度［3］是通过计算单个组件的可靠性变化对整个系统可靠性变化的影响程度来说明组件重要程度的一种计算方法。该重要度由系统可靠性Rs对组件Cj可靠性Rj求偏导来计算：

分析式（1）可知，若IjB值较小，说明即使当组件Cj发生较大的可靠度变化，相对系统可靠性也是较小的变化，那么对该组件进行设计时，就可以综合考虑经济性因素和可靠性因素，允许其可靠性相对低一些，对应的失效率相对大一些。通过这种方式，我们就可以对一个组件的重要程度进行判定，从而在设计中有的放矢。

对于雷达机械设备，系统和组件均只存在工作状态和失效状态，是一个二态系统（组件），因此系统（组件）的失效概率为

从而，可通过在雷达机械设备中常常使用的失效率对Birnbaum重要度进行表示：

将雷达机械设备的可靠状态表示为“1”，失效状态表示为“0”［4］。对于这种二态系统，可以进一步简化，使用全概率公式进行表示：

将式（3）代入式（5），可将二态系统下，组件失效独立时，该组件的Birnbaum重要度写成：

3 基于应力强度干涉模型的系统重要度计算原理

在雷达机械设备中，一个组件的自身强度能够对设备可靠性、失效率产生较大影响，而对一个组件的强度（strength）产生影响的因素很多，其中，最主要的是其所受的环境应力（load）。当组件所受强度大于应力时，组件就可正常工作；当组件所受强度小于应力时，组件则会遭到破坏，从而导致失效。而对于应力和强度，一般可以通过相应的概率密度分布进行表示，在雷达机械设备中，往往会根据实际的使用环境和使用要求对可靠性指标进行约束，在这种条件，允许雷达机械设备零组件的强度在一定概率下小于应力［5］。

图1 中阴影部分组件就是组件为失效组件，但系统可靠性可接受的范围。因此，可以通过以下公式对组件的可靠度进行计算［6］

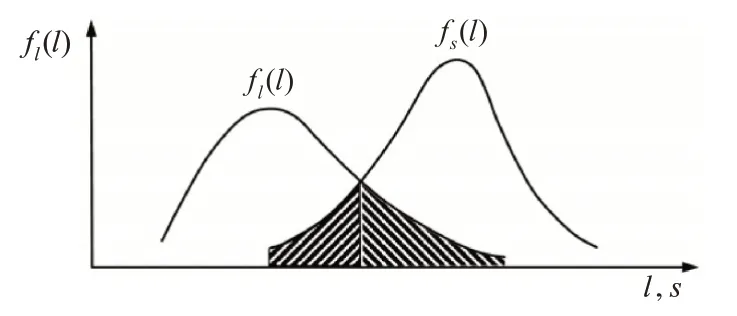
图1 组件强度和所受应力干涉模型图

式中，fl(l)、fs(s)分别为环境应力、强度概率密度函数，具体公式需结合组件和系统的特点决定。

结合系统可靠性和组件可靠性的表达方式，我们假设环境应力保持恒定，则可将重要度公式转换为关于强度变化表示［7］。

我们可用求导的概念将式（8）的Birnbaum 重要度写成极限形式［8］。设组件强度变化前系统和组件Cj的可靠度分别为Rs(sj1)和Rj(sj1)，变化后的分别为Rs(sj2)和Rj(sj2)，如下：

式中，Δsj代表组件可靠性在两个不同强度下的变化量Δsj=Rj(sj1)-Rj(sj2)。

2）生活习性。桃小食心虫在渭北果区每年发生1～2代，以老熟幼虫在土壤内结茧越冬。一般5月下旬至6月上旬越冬幼虫破茧出土，成虫多产卵于果实梗（萼）洼处。幼虫孵化后，蛀入果实，在果实内蛀食20天左右，老熟后咬破果皮，脱果而出；脱果早的在土表作夏茧化蛹发生第2代，脱果晚的入土越冬。6月下旬至7月上中旬出现第1代成虫，8月上中旬出现第2代幼虫，在采果前大部分脱果。

4 串联系统中应力强度干涉重要度的推导

在雷达的机械设备中，各个组件通过各种连接方式紧密相连，一个组件失效，就会导致整个系统的失效，因此雷达机械设备中，组件的连接方式主要为串联连接［9］。

由于雷达机械设备所受的环境应力一般为恒定应力，因此可将系统中组件的失效概率表达为关于组件强度的函数［10］。

图2 是串联系统的可靠性框图，根据串联系统一个组件失效则整个系统失效的特点，可以获得组件失效相互独立时系统的可靠度如下：

图2 串联系统可靠性框图

式中fsi(s)是组件Ci强度所服从分布的概率密度函数。

可将系统可靠度进行表示，即

将式（10）代入式（11）可得：

式中，Fsi(l)为应力l作用下组件Ci的失效概率。

因此，可将串联系统，组件失效情况相互独立情况下的强度应力干涉可靠度模型进行表示

设组件强度的概率密度函数为fsi(l)，i=1，…，j-1，j+1…，n，承受的环境应力概率密度函数为fl(l)，组件Cj强度初始概率密度函数为fsj1(s)，变化后的为fsj2(s)。系统中有且只有组件Cj的强度发生变化，组件变化前后系统可靠度的变化量为Rs(t1)-Rs(t2)，有

同理可得，组件j可靠度的变化量为

将式（14）和式（15）代入式（11）可得串联系统的重要度表达式，有

根据式（8），对上式转化对于式（16）的分子分母同除以强度的变化量［11］，得

将上式转换为导数表示［12］：

根据模型，由于fsj(∞)=0，可得：

若假设各系统中组件失效是相互独立的，按照推导式（19）的思路，利用式（15）的可靠性计算公式，得组件失效独立情况下组件Cj重要度公式为

式中Ri是组件Ci的可靠度。

对比式（19）和式（20）可以看出，一个组件的重要度由其余组件的可靠度情况共同决定，符合串联系统的特点［13］。

5 结语

本文首先提出了一种基于雷达机械设备的应力强度干涉模型，针对雷达机械设备串联系统的重要度计算方法。利用这种方法，可以对雷达机械设备进行综合分析，找出机械设备中的薄弱环节，从设计之初就对重要度较高的组件进行重点关注，通过试验、仿真等多种方式来进行重要部位的设计，从根本上提高雷达机械设备的可靠性。