钢筋混凝土梁桥弹塑性抗震分析方法研究

2023-08-30付发壮

企业科技与发展 2023年5期

摘要：为研究不同方法在分析普通钢筋混凝土梁桥弹塑性抗震性能时的适用性，文章建立了三跨全桥有限元模型，基于增量动力分析法提取集中塑性铰模型、纤维单元模型和等效线弹性分析方法在梁桥弹塑性抗震分析的计算结果，包括墩底弯矩、墩底剪力及墩顶位移指标，经对比分析，得到如下结论：①对于普通钢筋混凝土梁桥的双柱墩，进行静力非线性分析时采用集中塑性铰模型和纤维单元模型均可，两者计算结果相差较小；②采用等效线弹性法计算梁桥结构在弹塑性阶段的抗震性能指标与集中塑性铰模型和纤维单元模型的计算结果基本一致，在工程误差允许范围内；③采用简单的等效线弹性法进行计算可有效提高计算效率。

关键词：钢筋混凝土梁桥；弹塑性；等效线弹性；抗震性能

中图分类号：U442.5 文献标识码：A 文章编号：1674-0688（2023）05-0044-05

0 引言

钢筋混凝土梁桥作为我国桥梁结构中的主要形式，具有耐久性高、可维修性强、结构整体性好等优点，因此应用最为广泛。在地震灾害作用下，相比其上部结构，梁桥工程中的下部结构更易发生破坏且破坏程度更为严重，这些破坏可能会造成桥梁倾斜、梁体位移或弯曲等，难以维修和修复，严重时甚至导致落梁［1-2］。从过去的地震破坏经验中可知，梁桥工程在地震灾害作用下，其下部结构发生破坏时通常已处于弹塑性阶段，因此近年来国内外学者针对梁桥结构的弹塑性开展了大量的研究。张振浩等［3］对钢筋混凝土梁桥结构的弹塑性进行抗震研究，考虑多点非一致激励，结合桥梁结构设计基准期内抗震可靠度的计算结果和指标，对实际工程结构进行数值模拟分析，计算结果表明：采用结构可靠度理论与结构弹塑性分析相结合的方法，可有效获取设计基准期内梁桥结构在多种地震荷载作用下的结构抗震可靠度指标。该研究为钢筋混凝土梁桥结构的抗震分析和研究提供了一定的参考。李喜梅等［4］研究钢筋混凝土梁桥结构材料劣化对其抗震性能的影响规律，通过对比不同材料劣化程度、不同地震荷载作用下的结构应力和位移响应，提取梁桥结构不同时期的受力特性和破坏特性，明确了材料劣化和地震荷载对梁桥结构抗震性能的影响。该研究为钢筋混凝土梁桥的安全设计和管理提供了一定的参考。赵杰等［5］针对城市高架桥的抗震性能，利用OpenSees有限元软件，以某六跨连续梁桥为研究对象进行静力弹塑性和动力弹塑性分析，明确了桥墩的延性系数和承载能力以及地震荷载作用结构的变形和受力特性。

不同于前人的研究角度，本文研究纤维单元模型、集中塑性铰模型和等效线弹性分析方法在梁桥结构弹塑性抗震分析中的差异，通过Midas/Civil有限元分析软件建立全桥模型，基于增量动力分析法对比分析3种不同分析方法的墩底弯矩、墩底剪力及墩顶位移指标等梁桥的抗震性能指标，明确不同分析方法的适用性。

1 工程背景和模型建立

1.1 工程背景

本文以实际工程结构为背景，研究对象为三跨钢筋混凝土梁桥，该桥计算跨径为20 m+20 m+20 m=60 m；桥面净空为7 m+2×0.75 m人行道；桥梁等级为B类；桥梁设计车道数为2车道。

该钢筋混凝土梁桥的主要结构采用C30混凝土材料，包括主梁、桥墩、盖梁、横隔板和横系梁；桥墩截面是直径为1 m的实心圆形，墩柱采用普通钢筋混凝土双柱墩的形式，其结构外侧混凝土的保护层厚度为5 cm，结构主筋采用直径为25 mm的HPB400钢筋，结构箍筋采用直径为12 mm的HPB400钢筋，加密段桥墩的箍筋间距为0.1 m。

1.2 模型建立

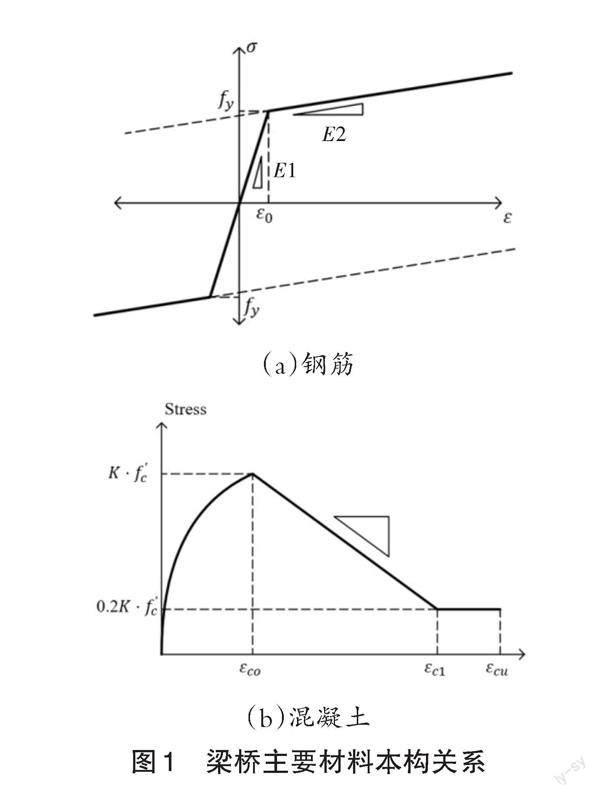
（1）采用Mander本构模型模拟约束混凝土材料，其中无约束混凝土的抗压强度数值为25 500 kN/m2，约束混凝土的强度数值为31 533.17 kN/m2，核心混凝土的有效面积为0.642 5 m2，有效约束面积为0.621 7 m2；采用中心对称的双折线形式模拟钢筋材料，其fy数值为400 000 kN/m2，弹性模量E为200 000 000 kN/m2，E2/E1=0.001。图1为钢筋和混凝土材料的本构关系，其中图1（a）中横坐标表示钢筋的拉应变、纵坐标为钢筋的拉应力；图1（b）中横坐标表示混凝土的压应变，纵坐标表示混凝土的压应力，K为系数，fc为混凝土轴心抗压强度。

（2）采用Midas/Civil有限元分析软件建立普通钢筋混凝土桥墩的全桥模型（如图2所示）。

1.3 模型分析方法

（1）建立普通钢筋混凝土梁桥结构的纤维单元模型和集中塑性铰模型，在此基础上与等效线弹性分析方法的计算结果进行对比。在对3种不同的方法进行对比时，采用通过直接积分得到动力时程的分析方法，并采用Newmark-β隐式积分法分析梁桥结构的地震下弹塑性时程数据。

（2）在对该梁桥结构进行抗震性能分析时，采用增量动力分析法（IDA）。对梁桥结构添加一个地震激励并进行记录，将记录作为基准，对该基准以一定比例的系数不断增加，以此分析不同等级强度地震激励下的结构动力时程响应，得到多条不同地震激励强度下的地震需求参数曲线，对曲线进行数据统计和分析即可得到不同地震強度下该梁桥结构的抗震性能。

（3）本文进行分析时，对该梁桥结构先施加一个加速度峰值为0.1 g的地震激励，并对该地震激励以0.1 g的递增速度增大，增大至1.0 g，选取该时程响应结果和人工地震波计算结果的最大值评估结构的抗震性能。人工地震波参照参考文献［6］选取。

2 Pushover分析

为得到该梁桥结构顺桥向、横桥向的能力谱图，对梁桥双柱墩进行2个方向的静力非线性推倒分析，即Pushover分析。

2.1 顺桥方向

对梁桥结构的集中塑性铰和纤维单元2种模型进行顺桥方向的Pushover分析，结果见表1。

2.2 横桥方向

对梁桥结构的集中塑性铰和纤维单元2种模型进行横桥方向的Pushover分析，结果见表2。

由表1和表2可知，采用集中塑性铰或纤维单元模型对该梁桥结构进行分析，计算结果相差不大，不同模型的计算结果误差较小，吻合度较高。

3 抗震性能分析

3.1 集中塑性铰模型

在对该梁桥结构的集中塑性铰模型进行抗震性能分析时，施加递增的人工模拟地震波和人工地震波，地震PGA值的范围在0.1～1.0 g，选取其结果中的最大值进行分析，同时考虑梁桥结构的顺桥方向和横桥方向2个方向上的动力时程响应。该梁桥结构的集中塑性铰模型计算结果如图3所示。

由图3可知，采用集中塑性铰模型对结构进行计算时，当加速度达到0.4 g，结构开始进入屈服状态；当加速度达到0.9 g，结构开始完全丧失承载能力；二者之间，结构一直处于屈服状态。

3.2 纤维单元模型

在对该梁桥结构的纤维单元模型进行抗震性能分析时，荷载工况与集中塑性铰模型类似，需同时考虑梁桥结构的顺桥方向和横桥方向2个方向上的动力时程响应，进行纤维单元模型计算时可考虑其局部伤损情况，并考虑轴力弯矩或弯矩与弯矩之间的相关关系。该梁桥结构的纤维单元模型计算结果如图4所示。

由图4可知，采用纤维单元模型对结构进行计算时，当加速度达到0.4 g，结构开始进入屈服状态；当加速度达到0.8 g，结构开始完全丧失承载能力；二者之间，结构一直处于屈服状态。

3.3 等效线弹性分析

我国的桥梁结构抗震设计通常分为2个阶段，即E 1地震波阶段和E 2地震波阶段。桥梁结构在E 1地震波的作用下应处于弹性阶段，而在实际的桥梁结构延性设计工作中，允许桥梁结构进入E 2地震波阶段，代表在E 2地震波作用下桥梁结构的位移如果不大于容许位移，即认为不会倒塌，因此按照《公路桥梁抗震设计细则》，该梁桥结构在E2地震波作用下，其墩顶水平位移[?d]的顺桥方向和横桥方向如下：

[?d=cδ] （1）

公式（1）中，[δ]为采用截面有效刚度法得到的E 2地震波作用下的墩顶水平位移；[c]为调整系数，当结构周期T≤0.1 s时，取值1.5，当T≥Tg时取值1.0，其他位置按照线性内插法获得。

在进行等效线弹性分析时，水平设计反应谱与施加的地震作用强度要兼容，并且根据上文的计算结果，当梁桥结构进入屈服阶段即峰值加速度达到0.4 g时，计算墩顶水平位移时使用截面的有效刚度（即建模时屈服阶段的桥墩截面采用折减刚度），经弯矩曲率计算得出顺桥方向和横桥方向的折减系数分别为0.37和0.29。该梁桥结构的集中等效线弹性法计算结果如图5和图6所示。

4 结果对比分析

根据“3.3节”的计算结果，对比分析梁桥结构的纤维单元模型、集中塑性铰模型和等效线弹性分析方法。

4.1 弯矩结果对比

对比分析3种方法的墩底弯矩计算结果，如图7所示。采用等效线弹性法计算的墩底弯矩结果与其他2种方法的结果十分接近，顺桥方向和横桥方向差别最大的位置均为当峰值加速度为0.3 g时，等效线弹性与集中塑性铰之间也只相差12.9%，而纤维单元模型与集中塑性铰模型的计算结果误差很小，在10%内。

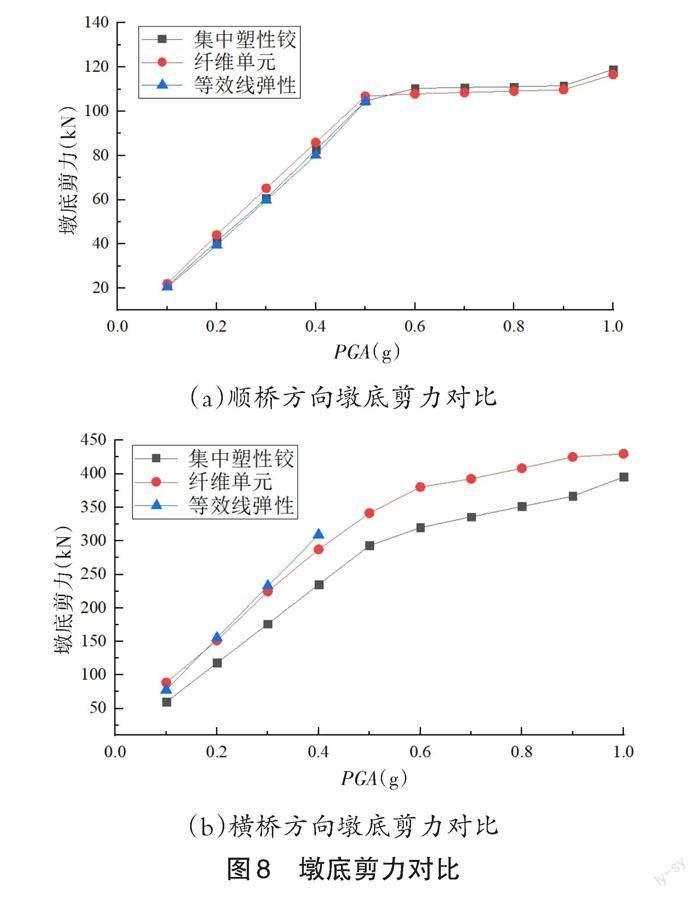
4.2 剪力结果对比

对比分析3种方法的墩底剪力计算结果，如图8所示。在顺桥方向采用3种方法的计算结果相差均很小，在工程误差允许的范围内可以忽略不计；在横桥方向上采用等效线弹性法分析的结果与其他2种方法的结果误差较大，达到26.5%，而纤维单元模型、集中塑性铰模型的计算结果相差也较大，达到18.8%，主要原因是三者考虑的结构塑性状态开始时的地震波的峰值加速度不同。

4.3 位移结果对比

对比分析3种方法的墩底弯矩计算结果，如图9所示。在顺桥方向采用等效线弹性法与其他2种方法相比，计算结果相差不大，墩顶位移发展规律相近，峰值加速度为0.3 g时，等效线弹性模型与纤维单元模型的误差值最大，为21.6%；在横桥方向上采用等效线弹性法分析，其结果与纤维单元模型十分接近，而与集中塑性铰相比误差较大，误差值约25%。

5 结论

本文通过Midas/Civil有限元分析软件建立全桥模型，研究纤维单元模型、集中塑性铰模型和等效线弹性分析方法的梁桥弹塑性计算结果，基于增量动力分析法对比分析3种不同分析方法下普通钢筋混凝土梁桥双柱墩的墩底弯矩、墩底剪力及墩顶位移等梁桥的抗震性能指标，主要结果如下。

（1）对结构进行静力非线性分析，采用集中塑性铰模型和纤维单元模型均可，计算结果相差较小。

（2）采用等效线弹性法计算梁桥结构的墩底弯矩、墩底剪力及墩顶位移等弹塑性阶段的抗震性能指标，与集中塑性铰模型和纤维单元模型的计算结果相差不大，在工程误差允许的范围内。为提高计算效率，可采用简单的等效线弹性法进行计算。

6 参考文献

［1］闫晓宇，李忠献，韩强，等.多点激励下大跨度连续刚构桥地震响应振动台阵试验研究［J］.土木工程学报，2013，46（7）：81-89.

［2］李小珍，雷虎军.基于多点激励的刚构-连续组合梁桥行波效应分析［J］.桥梁建设.2012，42（6）：33-38.

［3］张振浩，隗磊军，杨伟军.多点非一致激励下钢筋混凝土梁桥弹塑性抗震可靠度分析［J］.世界地震工程，2016，32（4）：134-139.

［4］李喜梅，付阿雄.考慮材料劣化钢筋混凝土梁桥抗震性能分析［J］.兰州理工大学学报，2021，47（3）：139-145.

［5］赵杰，温林莉，王桂萱.基于OpenSees的城市高架桥弹塑性抗震分析［J］.公路工程，2021，46（5）：45-53，62.

［6］何圣.钢筋混凝土桥梁弹塑性抗震分析方法研究［D］.重庆；重庆交通大学，2015.

【作者简介】付发壮，男，广西河池人，任职于广西公路检测有限公司，工程师，研究方向：桥梁工程。