基于图谱增强和CNN 的旋转机械智能故障诊断

梁晓智，晋文静，金 超

（北京天泽智云科技有限公司，北京 100080）

0 引言

在过去的几十年内，故障诊断技术由传统现场故障诊断，到基于机理模型的自动诊断、基于浅层机器学习的“特征提取+分类器”的智能故障诊断、基于深度学习的智能故障诊断等，从过去依赖经验到现在弱机理和强数据驱动相融合的智能故障诊断，逐渐向着数字智能化方向不断发展[1-4]。党的十九大报告中提出，加快建设制造强国，加快发展先进制造业，推动互联网、大数据、人工智能和实体经济深度融合，在中高端消费、创新引领、绿色低碳、共享经济、现代供应链、人力资本服务等领域培育新增长点、形成新动能。随着国家战略的实施，越来越多的工厂开始自建信息数字化公司，在这一过程中，也开始重视建立和积累设备故障数据库，这为基于数据驱动算法应用于故障诊断领域提供了良好的数字化基础和实施机会。基于传统“人工特征提取+分类器”的浅层机器学习不仅强依赖于工程师经验进行针对性的特征提取和特征选择，而且当机械设备的运行负载、转速等工艺工况较为复杂时或故障样本较少时，诊断效果及通用性较差。由于浅层机器学习算法存在的不足，越来越多学者把深度学习算法应用到故障诊断领域[5-7]。李恒等[8-9]使用短时傅里叶变换的时频谱图像结合卷积神经网络应用到轴承故障诊断中，并验证了该方法具有一定的鲁棒性，虽然在故障预测效果方面有一定提高，但是存在着两个潜在不足：

（1）虽然将不同分辨率时频谱图像进行训练，而后取正确率高的时频谱作为最终训练的输入，但这也意味着在负载等工艺工况变化复杂的场景下，算法需要重新适配最佳时频分辨率，这也造成了算法的通用性和跨域性较差。

（2）根据Heisenberg 测不准原理，时间分辨率与频率分辨率是反比例关系，为提高频率分辨率就要降低时间分辨率，同时有任意小的时宽和任意小频宽的图像是不存在的[10]，所以单一时频谱图像在不同场景下会存在不确定性和偶然性，会对算法的鲁棒性和通用性产生潜在风险。

因此，本文提出一种图谱增强和卷积神经网络相结合的旋转机械智能故障诊断算法，通过图谱增强使得单一样本在有限的分辨率内蕴含更多的信息量，增强单一样本的表征能力，结合卷积神经网络的自动特征工程能力，实现端到端的智能故障诊断。最后通过实验，验证了经过图谱增强的样本比普通图谱的智能故障诊断效果更好、鲁棒性更强。

1 基本原理介绍

1.1 短时傅里叶变换

在实际生产环境采集的振动信号，一般是非平稳信号，为了能捕获信号的时变、非平稳信息，本文采用短时傅里叶变换时频谱作为建模图谱。

短时傅里叶变换（Short-Time Fourier Transform，STFT）是时频分析中一种常见的时频分析方法。STFT 的主要思想是将时间序列信号数据以固定窗口长度进行截取分段，假设在每一个分段内的时间序列信号是平稳信号，并对所截取的时间序列分段信号进行傅里叶变换。随着窗函数在时间轴上不断平移和运算，将得到每个窗函数局部的傅里叶变换频谱集合，最终形成短时傅里叶变换时频谱。

其中，x（t）表示时间序列信号，h（t-τ）表示一个以τ 时刻为中心的窗函数。

根据STFT 原理，其时频谱效果主要有两个影响：一是窗函数的选择，二是窗函数宽度。选择合适的窗函数可以减弱因为截取信号而造成的频谱泄漏，一个好的窗函数其频谱应该具备窄主瓣、小旁瓣，如此便意味着频谱能量集中且泄漏少。另外，窗函数宽度的选择主要是影响STFT 时频谱的相对时间分辨率和频率分辨率，窗宽度小则频率分辨率低，窗宽度大则时间分辨率低。

1.2 图谱增强

由于短时傅里叶变换所得到的时频谱受到测不准原理影响，STFT 不能同时满足高时间分辨率和高频率分辨率[10]，所以希望通过图谱增强技术来提高图谱的信息量，降低单一图谱的风险，使算法模型更好地学习到各种故障模式的特征现象。

在故障诊断领域引入卷积神经网络模型进行故障分类和预测，相当于把信号序列和谱分析问题转换为以图谱图像的计算机视觉的图像识别和分类问题[12]，因此在图谱增强方面借鉴计算机视觉领域的处理方法。通过构造不同窗宽度的短时傅里叶变换时频谱图像，然后将不同窗宽度的短时傅里叶变换时频谱图进行图像拼接，形成一个蕴含丰富信息的特征图谱，从而实现图谱增强。

1.3 卷积神经网络

卷积神经网络（Convolutional Neural Networks，CNN）是一种具有自动特征工程特性的端到端的神经网络模型，由于其在图像识别和目标检测等计算机视觉领域应用效果显著，而被广泛应用于计算机视觉、自然语言等领域，近几年来有越来越多学者将CNN 引入到故障诊断领域[11-13]。经过多年发展演变，虽然涌现出很多CNN 的变种网络结构，但是自从Lecun 等[14]提出LeNet-5 之后，CNN 的基础单元网络结构就被确定下来，基础单元网络结构主要由卷积层、池化层和全连接层组成（图1）。

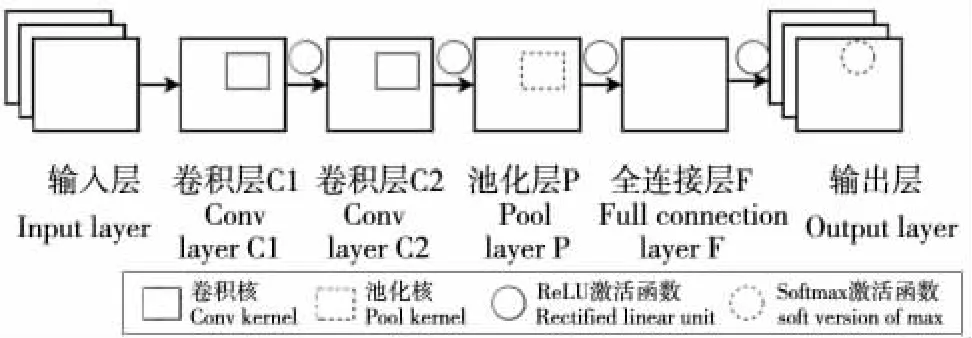
图1 卷积神经网络结构

1.3.1 卷积层

卷积层是卷积神经网络对输入层的特征数据进行特征提取的过程。卷积层通过设定的卷积核滤波器建立局部感受野连接和权值共享机制，并根据移动步长不断平移进行卷积运算而完成特征提取，结合激活函数可计算卷积层中每个神经元的输出值。

1.3.2 池化层

池化层是CNN 对卷积层所提取的特征矩阵进行下采样以达到特征降维的过程。池化层通过池化操作建立增大感受野机制，并根据移动步长不断平移进行池化下采样，在降低特征维度的同时又保留了有效的信息量，这对精简模型大小、提高运算效率以及增强特征的鲁棒性具有重大意义。池化层常见的方法有最大池化层、平均池化层等，本文采用最大池化层进行下采样。

1.3.3 全连接层

在经过卷积层和池化层之后，将特征矩阵展平为一维特征向量，以适应全连接层网络的分类器进行预测分类。本论文是个多分类任务，采用softmax 激活函数作为分类器，经过全连接层运算后，获得了K 个类别（-∞，+∞）范围内的分数zj。为了得到属于每个类别的概率，先通过es将分数映射到（0，+∞），然后再归一化到（0，1），Softmax 原理公式如下：

其中，yj表示第j 个类别占所有类别的概率，zj表示第j 个类别的分数zj，表示所有类别的分数zi的和。

1.4 自动特征工程

传统机器学习算法和深度学习算法在故障诊断领域的应用，属于行业机理知识和数据驱动技术深度融合的现代化主流模型，但两者在各个方面存在着本质性的差异。如对机理知识的依赖性，传统机器学习由于特征提取和特征选择需要一定的行业先验知识，因此强依赖机理知识。而深度学习则是弱依赖机理知识，即深度学习属于“弱机理+强数据”的算法模型。

CNN 的弱机理性体现在其能自动提取特征，通过卷积层的自动特征提取、以及池化层的特征选择和特征降维，对输入层特征图谱数据实现自动特征工程，最终形成分类预测所需要的特征向量数据。

1.5 网络参数优化

在模型训练时，CNN 常常由于网络结构复杂、网络层数众多以及网络参数量庞大等因素而容易导致深度学习模型在训练过程表现效果甚佳，而在测试集却表现一般的过拟合现象。另外，网络层数比较多的神经网络模型在训练的时候会出现梯度消失等状况。

为了缓解过拟合和梯度消失等问题，在设计CNN 结构时，考虑加入丢弃层Dropout 随机改变网络结构以缓解过拟合的风险，使得训练模型更具鲁棒性。本文选择ReLU（Rectified linear unit，线性修正单元函数）作为激活函数，其数学公式如下：

ReLU 激活函数不仅运算效率高，还能缓解梯度消失和梯度爆炸等问题[5]。

2 智能故障诊断流程

智能故障诊断流程可分为边缘数采数据获取、数据预处理、卷积神经网络和线上实时预测共4 个模块（图2）。

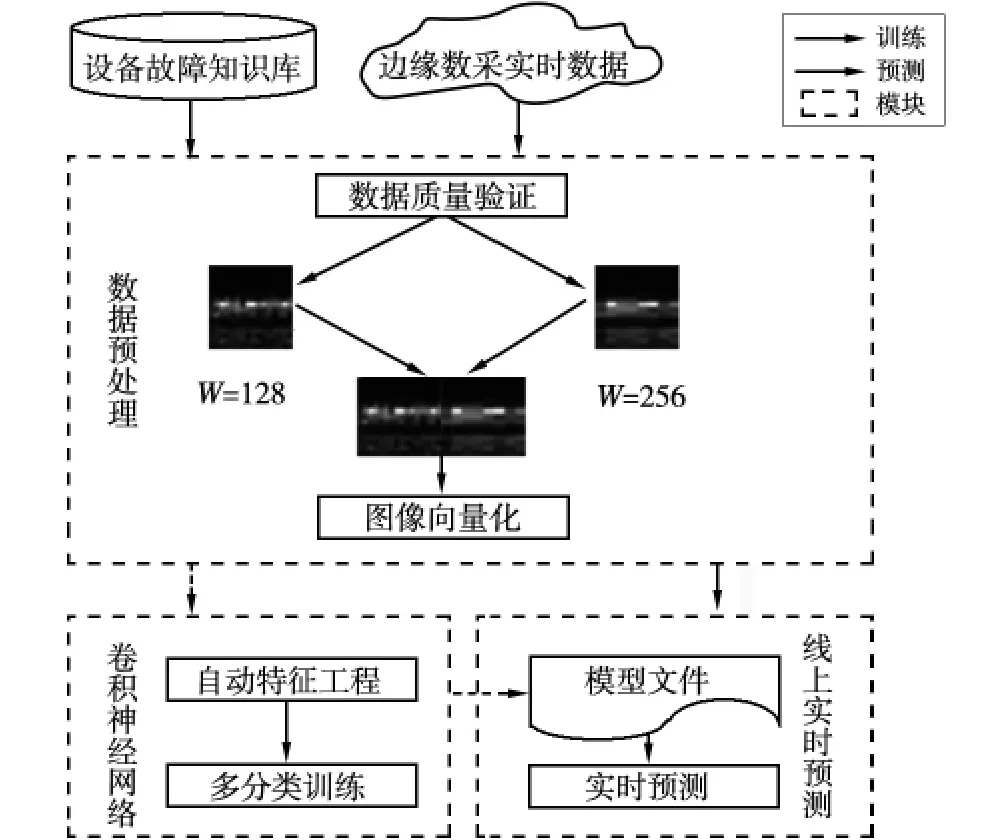
图2 智能故障诊断流程

（1）边缘数采数据获取模块主要分为故障知识库和云端边缘数采实时数据。设备故障知识库是企业积累的各种带有故障标签的故障数据集，主要为使用数据驱动算法提供训练集。而边缘数采实时数据则是通过边缘采集器通过云端传回的实时数据，用于线上实时预测的数据。

（2）数据预处理模块是线下算法训练和线上实时预测的公共处理模块。输入数据首先要进行数据质量验证，以判断当前输入数据是否有效，其次生成窗宽度（W）为128、256 的STFT 时频谱图像，通过图像拼接增强和丰富图谱的信息量，然后对图像进行结构化处理，形成图像向量，作为算法训练和预测的输入特征矩阵数据。

（3）卷积神经网络模块是针对输入的图像向量进行自动特征工程和多分类故障训练。卷积神经网络根据自身的卷积层进行自动特征提取，以此同时使用池化层进行自动特征选择和降维，形成全连接层分类器要求的特征矩阵之后，结合标签进行分类训练，经过性能评估达标后，将训练模型保存为模型文件，作为后续线上实时预测的预测模型。

（4）线上实时预测模块是针对边缘数采传回的实时数据进行线上实时预测。边缘数采实时数据经过数据预处理之后，将图像向量输入到卷积神经网络生成的模型文件中进行预测，然后输出预测的故障类别。

3 实验验证

本论文将采用美国凯斯西储大学公开的滚动轴承故障数据集进行实验，并验证所提出智能故障诊断方法的可行性和有效性。实验台装置如图3 所示，电机转速为1730～1797 r/min，采样频率为12 kHz 的驱动端轴承数据样本。

图3 实验台装置

3.1 数据集描述

实验样本分别取自于不同负载、不同转速下的不同故障尺寸的数据集。每一种故障类型都取负载为0、1、2、3 马力（1 马力=0.735 kW）的实验样本，其中内圈故障、滚动体故障和外圈故障（6 点钟方向）又分别取7 mils、14 mils、21 mils 故障尺寸的实验样本。详细样本信息以及故障类别标记情况如表1 所示，其中标签数为10 个，“×”表示不选取该样本、“√”表示选取该样本。

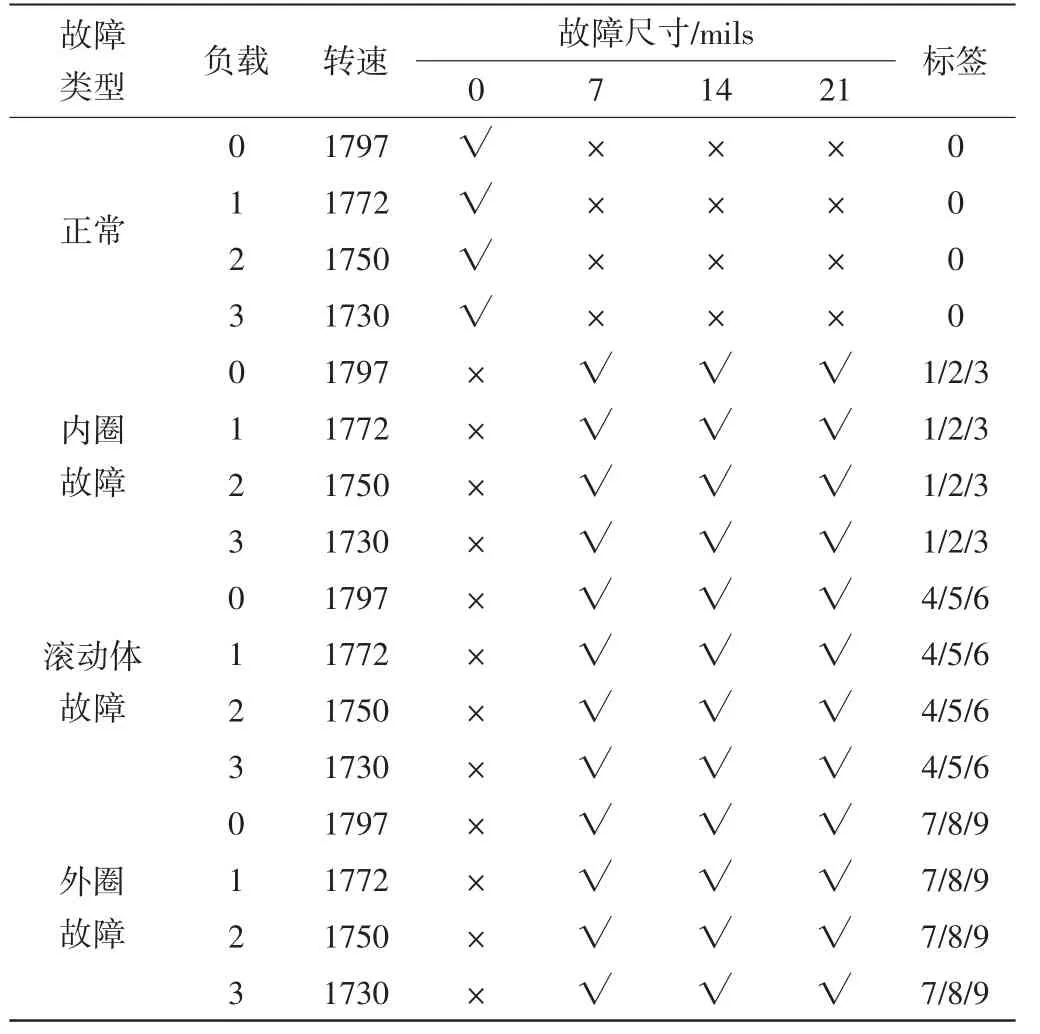
表1 实验样本和标签提取分布

正常数据样本标签为0，内圈故障的故障尺寸为7 mils 的样本标签为1，内圈故障的故障尺寸为14 mils 的样本标签为2，内圈故障的故障尺寸为21 mils 的样本标签为3，滚动体故障的故障尺寸为7 mils 的样本标签为4，滚动体故障的故障尺寸为14 mils 的样本标签为5，滚动体故障的故障尺寸为21 mils的样本标签为6，外圈故障的故障尺寸为7 mils 的样本标签为7，外圈故障的故障尺寸为14 mils 的样本标签为8，外圈故障的故障尺寸为21 mils 的样本标签为9。

为证明所提算法的可靠性和鲁棒性，根据原始数据划分为样本的策略不同，将划分为4 种实验数据集，详细情况如表2 所示。

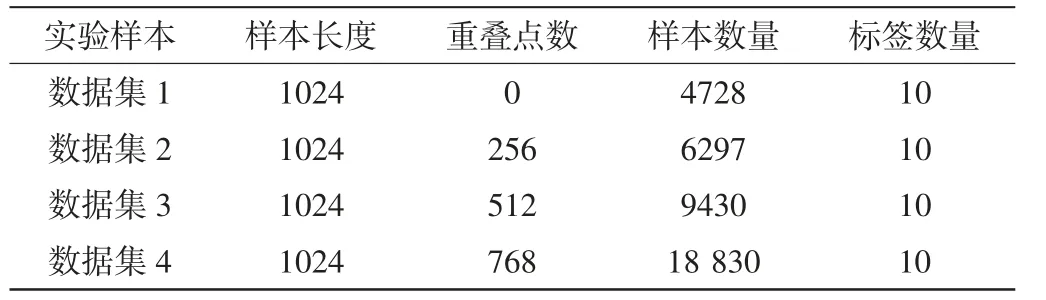
表2 实验数据集详情

由于振动数据是连续采集的时间序列数据，将采用滑窗方式对连续数据进行分段为一个个的样本数据，一个滑窗为一个样本。滑窗窗口为1024，重叠点数按照样本长度的重叠百分比0%、25%、50%、75%分别将原始数据按照相应重叠比例进行滑窗分段，分别对应着数据集1、数据集2、数据集3 和数据集4。数据集1 的所有滑窗前后没有重叠部分，即所有样本之间都是独一无二的。数据集2、数据集3 和数据集4 在滑窗过程中，前后两两样本之间分别对应着256、512 和768 个数据点的重叠部分。

实验样本图像有两种类型，详细信息如表3 所示。

表3 实验样本图像信息表

stft 图像是以汉宁窗且宽度为256 的16×16 像素的时频谱图像，而stft_enhance 图像是在stft_256 基础上结合汉宁窗且宽度为128 的16×16 像素的时频谱拼接成一个样本图像，以让一个样本蕴含更多信息，从而达到图像增强的效果。

3.2 卷积神经网络结构

本文在LetNet-5 基础上，结合本论文基于图谱增强的卷积神经网络智能故障诊断，从中寻找适应于智能故障诊断的卷积神经网络模型。

表4 中，卷积层C1 的卷积核大小为3×3、数量为32，卷积层C2 的卷积核为2×2、数量为32，池化层P 使用最大池化层大小为2×2、数量为32，全连接层F 大小1×1、数量256。

表4 卷积神经网络结构详情表

3.3 训练样本量对算法鲁棒性的影响

为了验证本文提出的stft_enhance 图谱增强样本在小数据集中比普通stft_256 图谱样本更具鲁棒性，通过划分测试集比例为0.9、0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1进行多次实验。本小节每个数据集圴为混合所有负载的样本数据，同时也包括所有故障类型，实验结果如图4 所示。

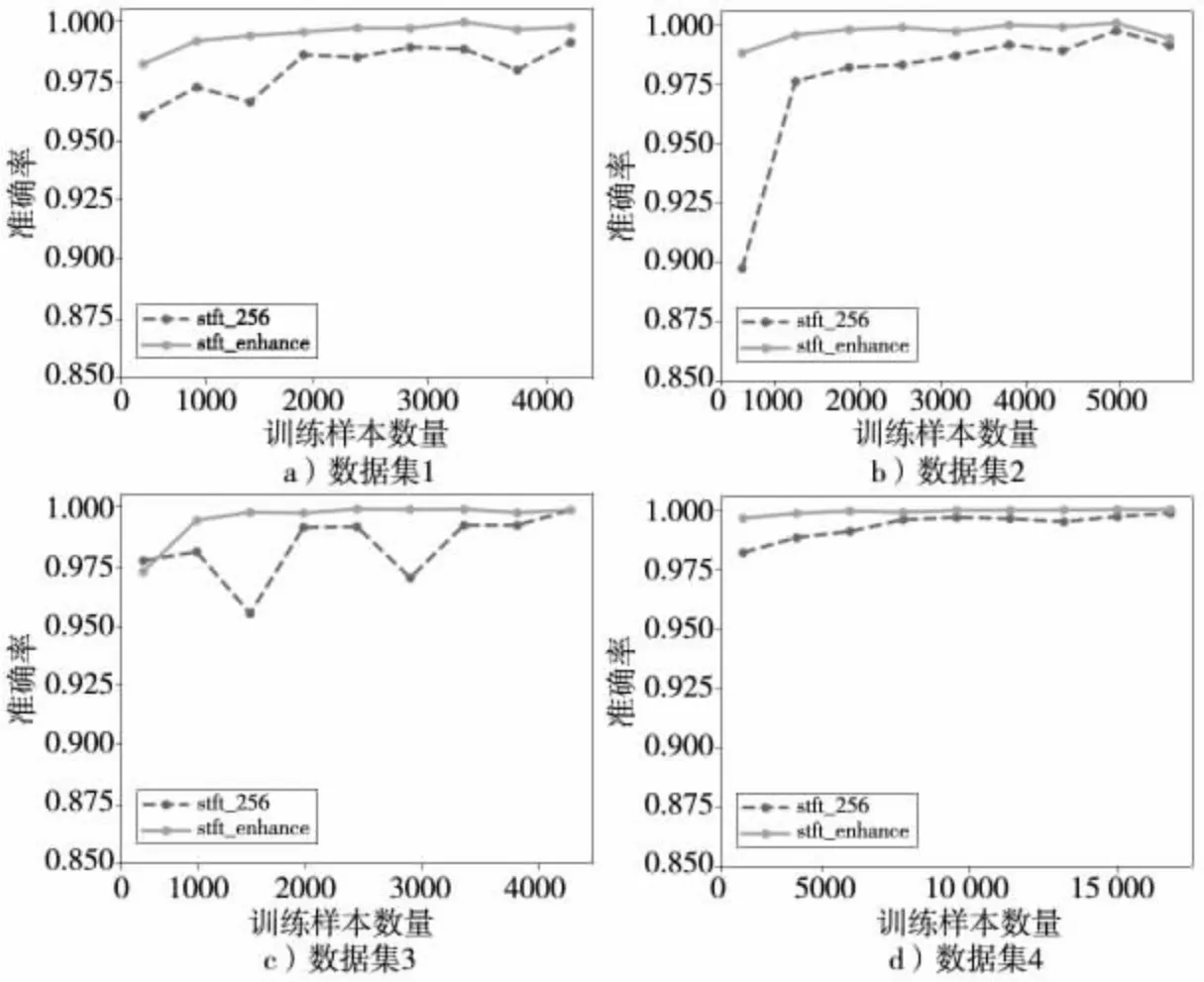
图4 训练样本数量与测试准确率曲线

根据图4 直观分析，基于stft_enhance 图谱增强样本的整体准确率曲线明显在stft_256 普通图谱样本的准确率曲线之上，这说明stft_enhance 鲁棒性更强。测试集比例为0.9 的小样本训练集的准确率统计情况见表5，其中stft_256 和stft_enhance 的平均准确率分别为0.954、0.985；训练样本数量与测试准确率的统计情况见表6。

表5 测试集比例为0.9 的小样本训练集的准确率统计情况

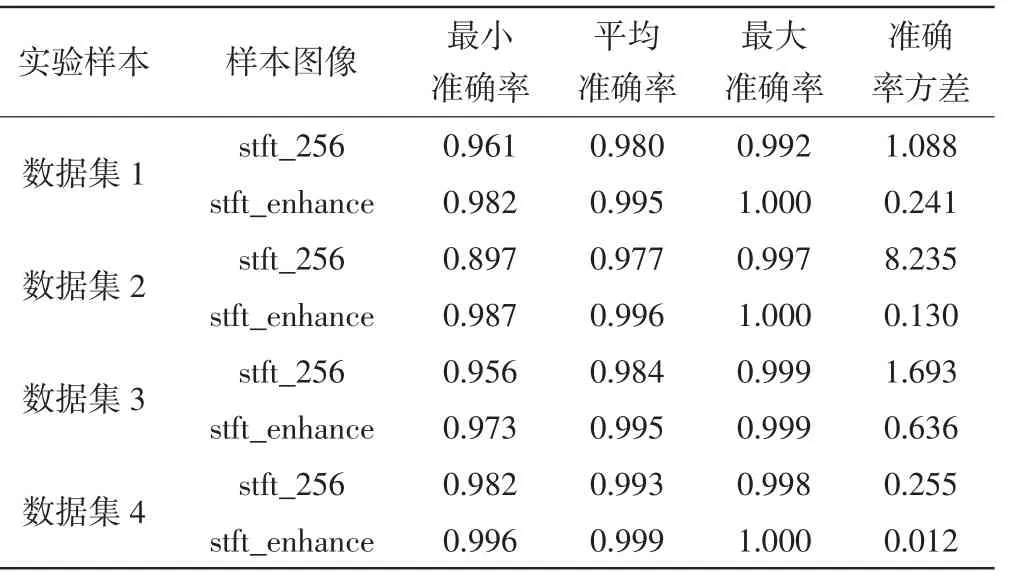
表6 训练样本数量与测试准确率的统计情况

结合图4 和表5、表6 分析，分析结论如下：

（1）小样本鲁棒性分析。由表5 可知，数据集1、数据集2 和数据集4 的stft_enhance，分别比stft_256准确率高2.3%、9.0%、1.4%；从平均准确率分析，stft_enhance 平均准确率为98.5%，而stft_256 平均准确率为95.4%。综合分析后认为，相比较于stft_256，stft_enhance 对小样本集更敏感。

（2）测试准确率曲线的稳定性分析。随着训练样本数量的增加，stft_enhance 测试准确率曲线总体呈上升趋势且变化较为稳定，在4 个数据集中，其最大方差为0.636，而stft_256 总体的测试准确率曲线波动较大，在4 个数据集中其最大方差为8.235。这说明stft_256 在应对不同训练样本数量时，其表征能力不够强大且容易受到干扰而导致局部误报情况。

（3）在4 种数据集实验中，stft_enhance 最低最小准确率为97.3%、最低平均准确率为99.5%、最低最大准确率为99.9%，而s tft_256 的相应数据分别为89.7%、97.7%、99.2%。由此可见，无论在4 种类型数据集中、还是小样本集或大样本集中，stft_enhance效果均优于stft_256。

3.4 变负载变转速对算法鲁棒性的影响

为了验证本文提出的stft_enhance 图谱增强样本在变负载变转速或单一负载与转速环境中比普通stft_256 图谱样本更具鲁棒性，本小节将采用固定比例随机划分训练集数量为80%，测试集数量为20%进行实验验证。其中，每个数据集处理为5 种工况数据，all 表示所有负载混合的样本数据且包含所有故障类型，0/1797 表示只取这个单一工况的样本数据且包含所有故障类型，1/1772、2/1750 及3/1730 也分别只取对应单一工况的样本数据且包含所有故障类型。

变负载变转速对算法鲁棒性实验的结果如图5 所示，其中all 表示所有负载和转速混合情况进行训练和预测，0/1797、1/1772、2/1750、3/1730 表示在对应的单一负载和转速情况下进行训练和预测。测试集比例为0.2 的all 的准确率统计情况见表7，其中stft_256 和stft_enhance 的平均准确率分别为0.994 和0.997，而在负载波动等维度的准确率统计情况见表8。

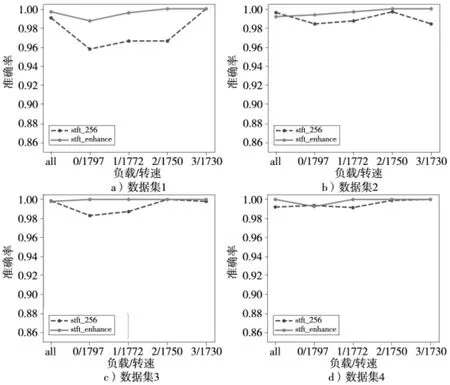
图5 在负载波动等维度的测试准确率曲线

结合图5 和表5、表7、表8 综合分析，得到的结论如下：

（1）变负载变转速鲁棒性分析。由表5 可知，在测试集比例为0.9 的小样本集中，stft_enhance 平均准确率为98.5%，而stft_256 的平均准确率为95.4%；由表7 可知，在测试集比例为0.2 的样本集中，stft_enhance 平均准确率为99.7%，而stft_256的平均准确率为99.4%；综上所示，stft_enhance 在小样本集中的变负载变转速鲁棒性明显优于stft_256，而在较大样本集中，略优于stft_256 的鲁棒性。

（2）单一稳定负载和转速分析。stft_enhance 总体测试准确率优于stft_256，而在数据集1 的小样本集中，stft_256 在0/1797、1/1772、2/1750 单一稳定工况下，其平均准确率96%，与stft_enhance 的99%相比差3%。

（3）总体准确率分析。stft_enhance 的测试准确率曲线总体在stft_256 的测试准确率曲线之上，另外，无论是在变负载变转速还是单一稳定工况下，stft_enhance 整体准确率优于stft_256的准确率。

3.5 强噪声环境对算法鲁棒性的影响

为了验证本文提出的stft_enhance 图谱增强样本在强噪声环境中比普通stft_256 图谱样本更具鲁棒性。本节实验除了对训练和测试样本施加10 dB 噪声之外，其他实验条件与上一节（变负载变转速对算法鲁棒性的影响）的实验条件保持一致。

根据图6 直观分析，在施加10 dB 噪声后，stft_enhance 和stft_256 的准确率曲线没有了相交点，这直观地反映了施加10 dB噪声后，stft_enhance 和stft_256 的准确率均受到了不同程度的影响。测试集比例为0.2 的all 的准确率统计情况见表9，其中stft_256 和stft_enhance 的平均准确率分别为0.971、0.994。

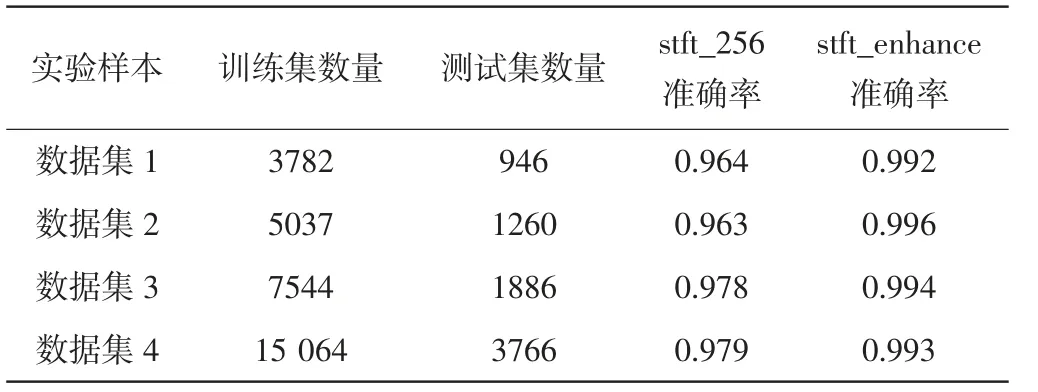
表9 测试集比例为0.2 的all 的准确率统计表（施加10 dB 噪声）

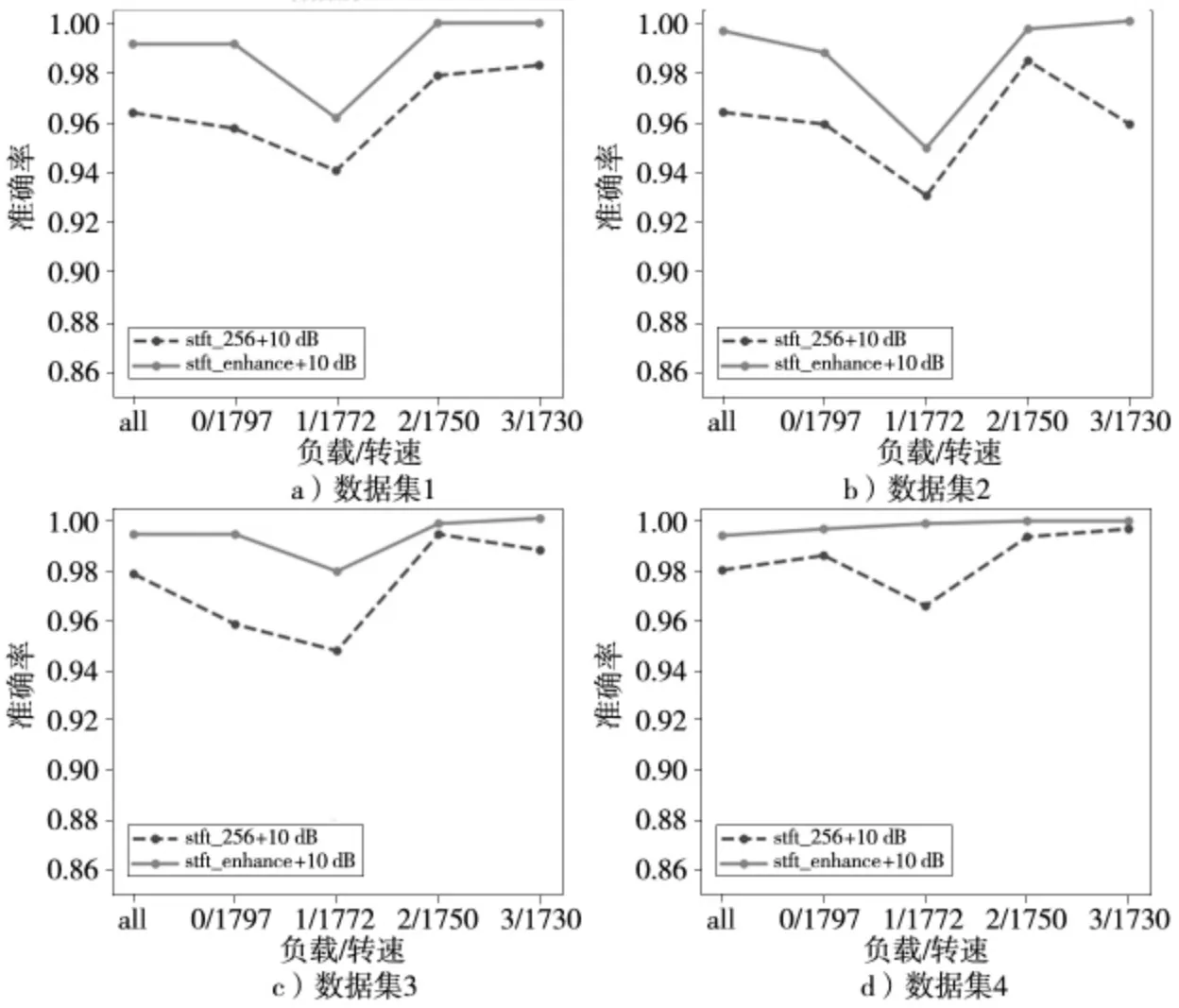
图6 在负载波动等维度的测试准确率曲线（施加10 dB 噪声）

施加10 dB 噪声，在负载波动等维度的准确率统计情况见表10。

表10 在负载波动等维度的准确率统计表（施加10 dB 噪声）

结合图6 和表7、表9，综合分析后可得到如下结论：

（1）强噪声环境下的变负载变转速鲁棒性分析。由表9 可知，stft_enhance 的平均测试准确率为99.4%，而stft_256 的平均测试准确率为97.1%，即在强噪声环境且变负载变转速情况下，stft_enhance 比stft_256 的测试准确率高2.3%。对比表7 未施加噪声的准确率，stft_enhance 平均准确率下降0.3%，几乎不受强噪声而影响算法的鲁棒性，而stft_256 平均准确率下降2.3%，说明stft_256 在强噪声环境抗噪性能较差。

（2）单一稳定负载和转速分析。stft_enhance 总体测试准确率优于stft_256，在施加10 dB 噪声后，1/1772 工况下的准确率波动最大，说明1/1772 受到噪声干扰时鲁棒性较差。

（3）总体准确率分析。stft_enhance 的测试准确率曲线总体在stft_256 的测试准确率曲线之上。另外，无论是在变负载变转速还是单一稳定工况下，stft_enhance 整体准确率优于stft_256 的准确率。

4 结论

本文提出一种基于图谱增强和卷积神经网络的旋转机械智能故障诊断方法。在使用美国凯斯西储大学公开的滚动轴承数据进行实验验证，相比较于单一图谱stft_256，图谱增强处理后的stft_enhance 结合CNN 的智能故障诊断具有以下优势：

（1）基于图谱增强和CNN 相结合的方法，在小样本集和大样本集中都具有较高的识别率和较强的鲁棒性。

（2）基于图谱增强和CNN 相结合的方法，无论是在负载稳定还是负载波动场景下，都具有较高的识别率和较强的鲁棒性。

（3）基于图谱增强和CNN 相结合的方法在施加10 db 高噪声环境干扰下，仍然具有较高的识别率和较强的鲁棒性。

除了在训练样本数目、负载波动和强噪声环境具有强泛化性和鲁棒性之外，相较于李恒等[8-9]提出单一时频谱像素64×64 及6 层的CNN（不包含输入输出层），本文的方法采用的图像分辨率（32×16）更小、CNN 结构（4 层）更简单，是一种集强鲁棒性和强泛化性的轻量级算法模型，这为算法模型部署到边缘端提供了友好性。

致谢：本论文由北京科技新星计划资助。