数据挖掘在油液监测故障诊断的应用

康鑫硕，崔 策

（1.广研检测（广州）有限公司，广东广州 510700；2.广州机械科学研究院有限公司，广东广州 510700）

0 引言

油液监测的异常值是指样本中某个特征与其余样本有明显差异的少数值。在油液监测过程中，对异常数据的甄别是一项重要工作，一方面，异常值的存在会对指标阈值的制定产生影响，多数情况下会导致报警值过于宽松，这样就容易造成漏诊，因此在制定阈值前通常要先将离群值从数据集中剔除；另一方面，异常值本身也表征这设备状态的异常，将这些离群点找出来并针对性地分析原因，也可以累积诊断经验，为企业的润滑管理的提升提供依据[1]。

通过异常值的检验，一方面提升了样本的净度，另一方面也是数据探索过程的重要一环，目前学术界有多种方法可以实现异常值的检验。例如，对于一维数据，其特征可以是样本的均值、方差等参数，采用统计图表等方式直接观察发现异常点；对于多维数据，可通过非监督算法如Kmeans、PCA 主成分等算法计算相应特征，并找出数据的特征中与多数数据存在明显差异的异常值[2]。本文分别介绍HBOS（Histogram-based Outlier Score，直方图）法、LOF（Local Outlier Factor，局部离群因子）算法、KNN（K-Nearest Neighbor，K-近邻）算法、ABOD（Angle-Ba sed Outlier Detection，角度离群算法）、Kmeans 算法等、Isolation Forest（孤立森林法）的检验原理，最后通过python 开发异常检验模块界面。

1 基于多元算法的异常值检验

1.1 直方图（HBOS）法

直方图法是一种基于统计的无监督方法，利用直方图去判断异常值。其核心思想是将多维样本的每个维度先进行直方图统计，计算出各维度的频数和频率等特征，然后进行合并计算，将多维样本分成多个方形区间，样本数少的区间是异常值的概率大，反之则为非异常样本，异常值的判别通过概率密度进行计算。图1 为一个通过直方图检验油液黏度—酸值二维数据异常值的示例，图中虚线外深色区间的数据为异常值[3]。

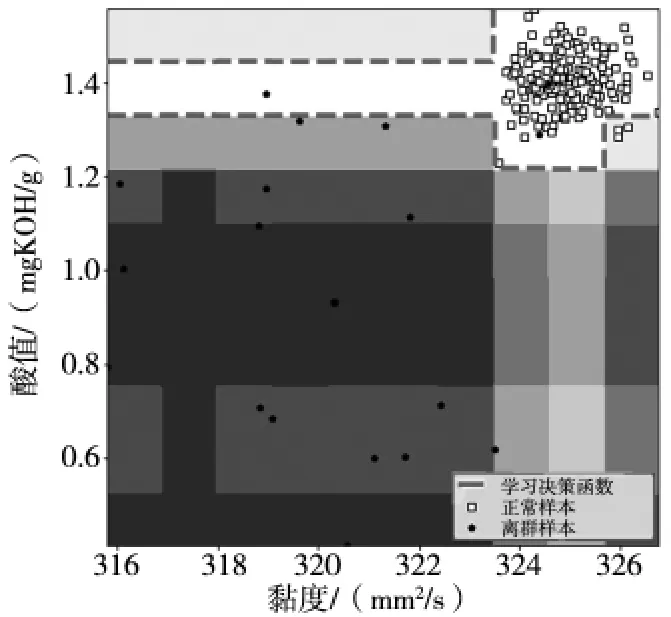
图1 HBOS 异常值统计示例

1.2 基于密度的异常值检验方法

从数据密度的角度来看，正常样本往往处于高密度区域，异常值往往是处于低密度区域中。基于密度的异常值检验方法的原理是：对于数据集D，其中多数正常样本xc周围的密度与其相邻样本的周围密度是相似的，而少数离群样本xo周围的密度会明显不同，通过对比各样本周围的密度和其相邻数据周围的密度，就可以获取离群值的相关信息[4]。

LOF 算法就是一种基于密度的异常值检验方法，可通过点的一定范围内数量来计算得出密度，某个样本周围的样本越少密度越低，数量越多密度越高。CBLOF（Cluster-Based Local Outlier Factor，基于聚类的本地异常因子）在LOF 的基础上增加了聚类的操作，降低了异常值检验的复杂度。图2 是通过CBLOF检验的同一组实验样本黏度和酸值之间的异常值检测结果。

1.3 基于距离的异常值检验方法

如果一个数据样品远离大部分点，那么就可以认为这个样本就是异常的。因此对于样本数据集D，可以通过统计计算出距离的阈值r 来划分样本数据的合理邻域。对于每个样本xi，可以考察xi与其他样本的距离特点。通过遍历计算出样本点xi和其余样本的距离，当某个点总是远离其余样本，即不在xi的r 邻域内，则xi视为异常值，这就是基于距离的异常值检验方法的基本思路[5]。

临近算法（KNN）就是最常见的基于距离的异常值检验方法，图3 是其检验的结果示例，其中距离函数选择欧式距离。

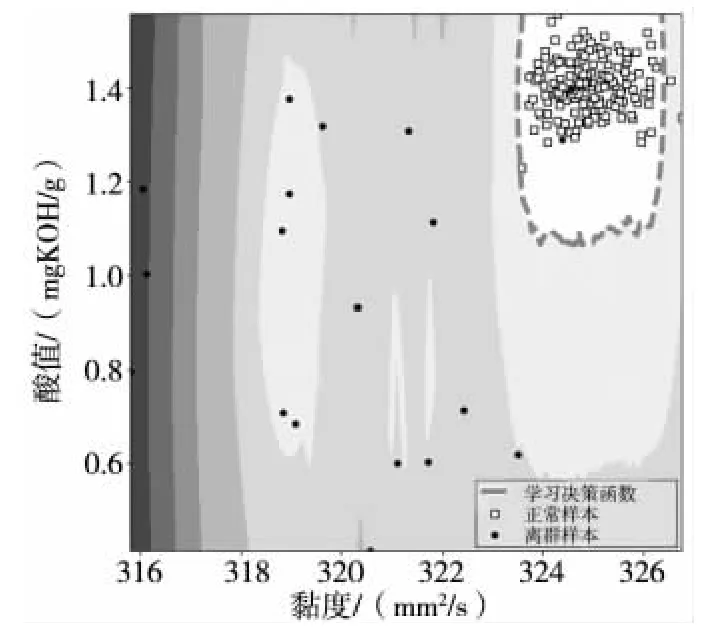
图3 KNN 异常值统计

1.4 基于角度的异常值检验方法

基于角度的离群点检测是一种针对多维数据集的检测方法。该方法类似于LOF 等局部离群点检测方法，对于数据集中任意的三点形成角度谱相图，然后通过设定表征离群程度的离群系数，将数据对象排序输出，最终得出离群点。由于高维数据的角度相比距离更加稳定，因此主要应用于高维数据的异常值检验[6]。常见的方法有角度离群算法（ABOD），图4 是其检验的黏度和酸值之间的异常值检测结果。

1.5 孤立森林法

孤立森林法（Isolation Forest）是一个基于集成学习的快速异常检测方法，适用于非线性、多维度的大数据样本的异常处理。从统计学来看，在多维数据空间里，异常样本值可定义为那些分布稀疏，且相比高密度群体较远的点。而往往异常值的稀疏特征可在通过遍历维度的方式找出，这就是“孤立森林”法的前提假设[7]。

孤立森林的计算原理与随机森林相似，它是基于多个决策树集成建立的。其思路如下：对于一组样本数据，在这个样本数据某个维度下的选择一个值，对样本群体进行二叉划分，将小于该值的样本划分到节点左边，大于该值的样本划到右边，这样就得到了一个分裂条件和两个数据样本，然后分别在这两个数据集上重复上面的过程，直到样本无可再分，这样就形成了一棵“树”[8]。每一个节点就可以看作一个分枝，每一个数据就可以看作一片叶子（图5）。终止条件通常有两种，一种是数据分身不可再分，即该数据集中只剩下一个样本，或全部样本值相同；另一个是数的高度到达一定程度。

图5 孤立森林法示意

把“树”建立好之后，通过不同的树集成形成孤立森林后，就可以对数据进行分类了。其过程就是将样本数据沿着不同树的枝干分类，最终达到不同的节点，并记录这个过程中经过的路径长度，即从根节点，穿过中间的节点，最后到达叶子基点，所走过的“枝”数量。在这种随机分割的策略下，异常值通常具有较短的路径。

孤立森林将异常数据判定为树平均路径较短的结果，并通过异常系数来评价一个数据样本的异常程度，其结果介于在0和1 之间，异常值公式为：

其中，E（h（x））是某树根节点到叶节点的路径长度h（x）的平均值，而c（n）是在n 个决策树h（x）的平均值。可以通过该公式对每个样本进行异常评分，数据遍历的树越多或路径越长则得分越低，反之得分越高。

图6 为通过孤立森林算法得出某齿轮油酸值和黏度的异常值结果。

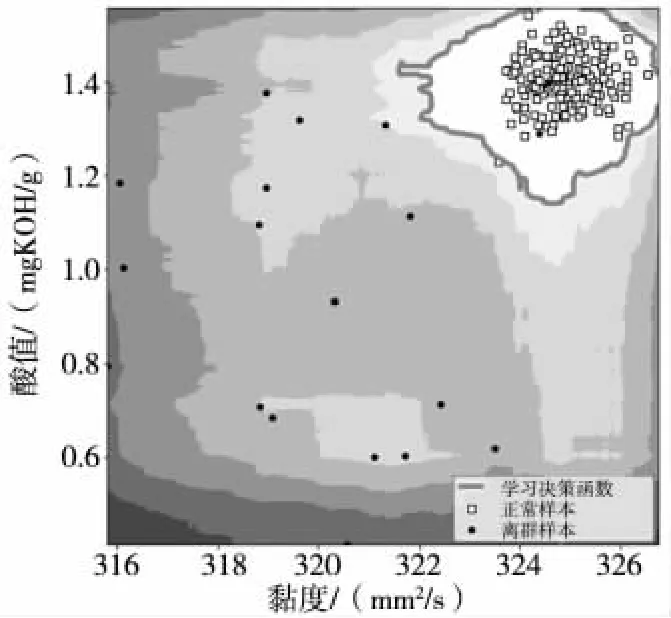
图6 孤立森林法异常检验

2 基于Kmeans 算法的数据探索

在设备的状态监测过程中，由于缺乏可靠的历史资料，往往无法确定共有多少故障类别，在仅有监测数据的条件下，通过对数据特征的统计分析，可以将具有相近特征的数据组成的一个类别，而对不同特征的数据划入不同的类别，即本着同类相近、异类相远的原则对数据进行区分，首先形成多个不同类别的特征集，而后通过计算特征集合内各点和中心的距离，以此来完成异常值的区分[9]。下面以Kmeans 算法为例，介绍聚类分析算法在异常值检测中的应用。

Kmeans 算法的核心思想是将所有样本数据到划分到不同数据簇当中，使得样本到聚类中心的距离平方和最小[10]。设样本模式集为X={Xi，i=1，2，3，…，N}，其中Xi为n 维向量，Xi={ Xik，k=1，2，3，…，n}，聚类过程就是要找到划分簇集ω={ω1，ω2，…ωC}，使得聚类准则函数J 到最小。

当各类中心明确时，类别的划分按照最邻近法则确定。即如果满足，则说明样品Xi属于类j。当获得多个不同簇后，计算每个点到簇中心的距离值，将距离跟设置的阈值相比较，如果其大于阈值则认为是异常，否则正常。

图7 是通过Kmeans 算法得出的酸值和水含量含量的聚类分析结果，从聚类结果可以知道数据的大致分类情况，这对于诊断工程师具有一定辅助诊断和数据探索的作用。

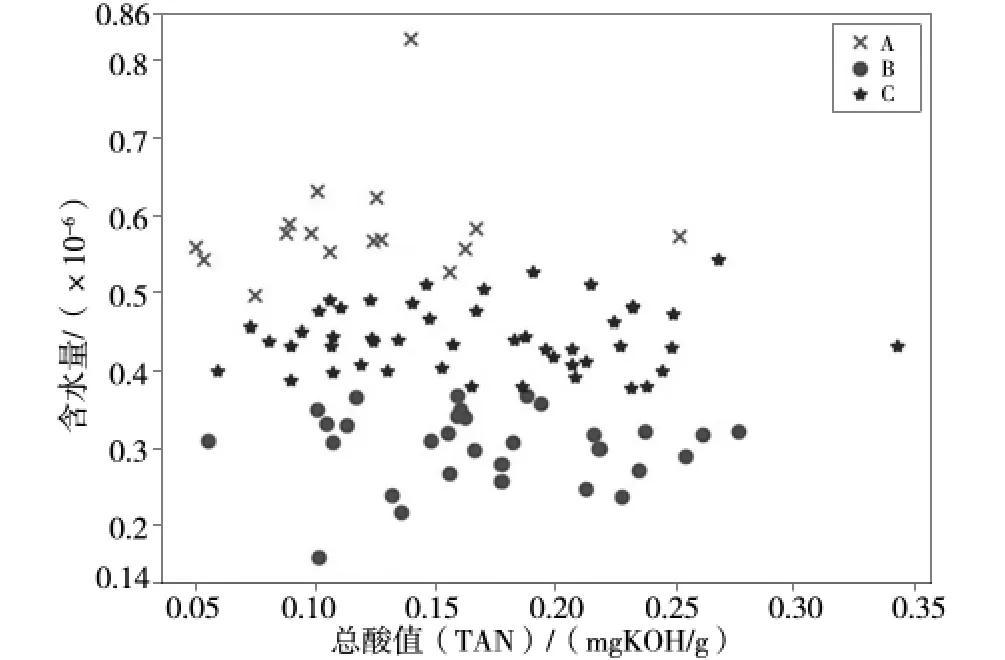
图7 Kmeans 算法异常值检验

3 功能开发

Tkinter 是基于python 语言开发的窗口视窗设计模块，具有标准GUI（Graphics User Interface，图形用户界面）工具接口。作为python 语言内置的GUI 开发工具，可快速、高效地创建GUI程序。Tkinter 能够满足多数小型GUI 程序的需求。其开发的程序在Windows、Linus 等操作系统上均可运行，具有较高的兼容性[11]。其中，数据库来源于Oracle 油液监测数据库，分析维度为油液监测数据的各项理化指标，如黏度、水分、温度等；异常值比例默认为0.3%，分析结果均显示在右侧（图8）。

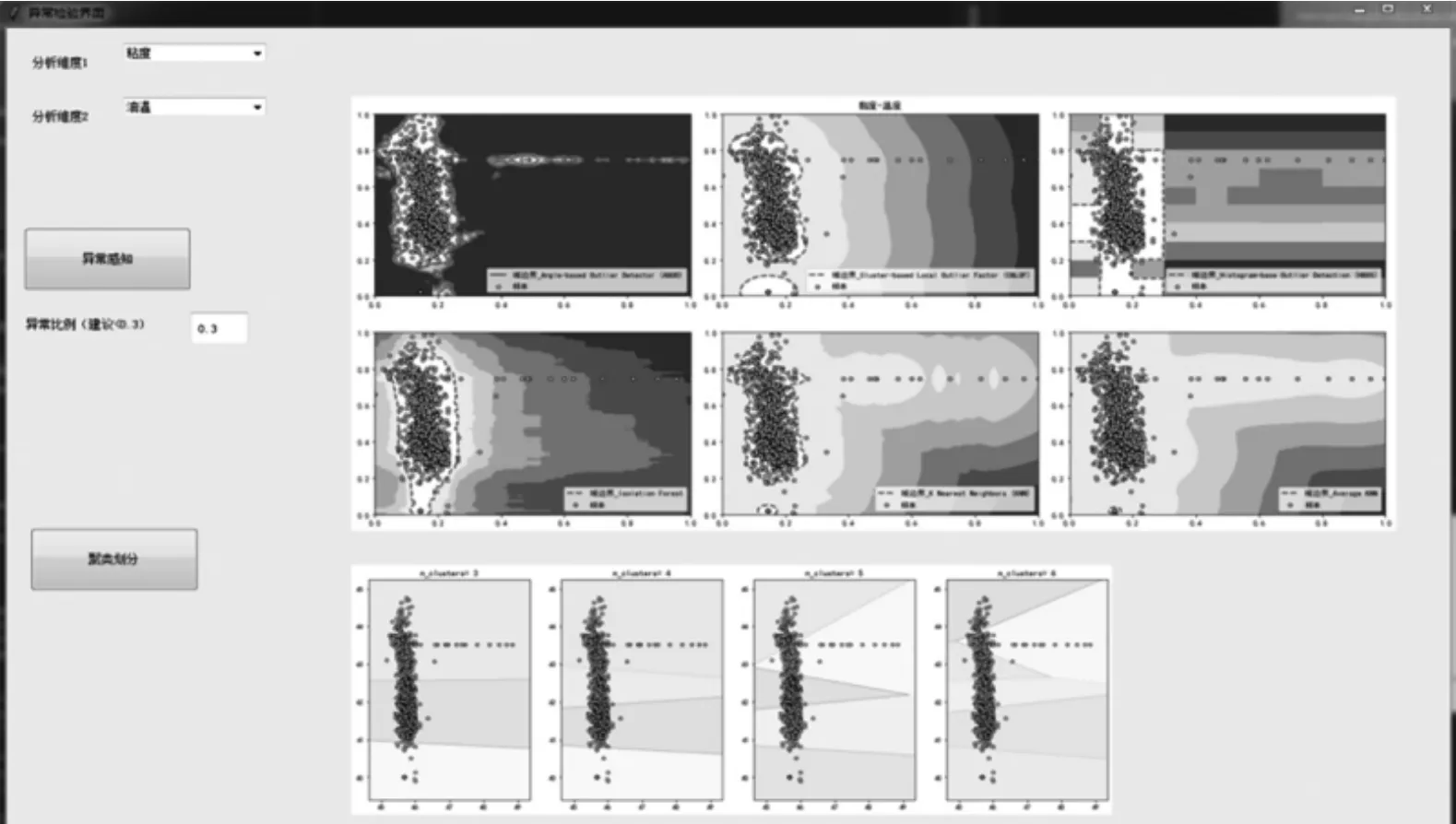
图8 基于Tkinter 开发的界面效果

4 总结

油液监测数据包含了设备故障状态的重要特征，作为设备是否检修与维护等操作的重要依据，如何感知多维、非高斯油液数据的状态，尤其是异常状态是挖掘数据和异常检验的难点，本文主要介绍直方图（HBOS）、LOF、KNN、ABOD、Kmeans、Isolation Forest（孤立森林）等多个算法的原理，并采用python Tkinter 开发异常检验界面，实现对油液监测数据的自动化探索和异常感知。