基于线性矩阵不等式的水电机组调节系统滑模容错控制

胡志平，邹屹东，陈金保，郑 阳，肖志怀

（1. 湖北白莲河抽水蓄能有限公司，湖北 黄冈 438600； 2. 武汉大学动力与机械学院，湖北 武汉 430072）

0 引 言

在国家“双碳”背景下，光伏与风电在电网中的装机容量不断扩大。为了加强电网的安全与稳定性，水电能源作为一种优质的调峰调频电源，将更加频繁地参与电网功率调节，对水电机组调节系统提出了严峻挑战。调节系统是水电站系统的重要组成部分，影响着机组乃至互联电网的安全稳定运行。针对上述问题，在过去的十年中，水电机组调节系统的控制技术已得到广泛研究，极大提高了调节系统的运行可靠性、可用性和安全性。

PID 控制是一种经典的、广泛使用的工业控制方法，在水轮机调节系统中应用广泛。文献［1］提出了光伏功率扰动环境下的水电机组模糊PID 控制研究。黄金龙等人［2］研究了一种利用神经网络与智能算法的自适应PID 控制器，以有效提高调节系统的控制质量。文献［3］提出了一种基于迭代学习的用于调节系统在线参数优化方法，用以提高风电功率波动环境下水电机组稳定性能。尽管PID控制具有在线计算量小、易于程序实现、实时性好等优点，但其控制参数的设定通常只针对几组固定工况。在“双碳”背景下，电网灵活运行要求越来越高，水电机组运行工况常发生大范围变动，固定的PID 参数可能导致控制器性能下降。随着控制理论与应用的研究不断发展，一些新颖的控制理论被应用到水轮机调节系统设计中，如自适应控制［4］、鲁棒控制［5］、神经网络控制［6］等，但上述大多数控制方案都是基于控制器不会失效的假设而提出。

容错控制可以消除或抑制机电系统控制信号的不确定性与扰动影响［7］。文献［8］提出了基于模糊观测器的容错控制方案，并对故障影响执行机构的风机进行控制，从而确保转速跟踪给定参考转速少受执行机构故障影响。文献［9］使用自适应时间延迟控制对具有同时执行器和传感器故障的风力涡轮机进行容错控制。上述文献均针对风电机组进行容错控制研究，但目前关于水轮机调节系统容错控制的研究较少。作为优质的调峰调频电源，水电机组的调节系统能够在部件或子系统发生故障的情况下，仍然保持较好的性能十分重要。此外，由于机组过渡过程可能会对水电站系统造成较大损害［10］，而滑模控制可以保证系统在较短时间内稳定，具有改善系统过渡过程的优点［11］，因此，本文将容错控制与滑模控制相结合，设计了基于线性矩阵不等式的水电机组调节系统滑模容错控制策略，包含等效滑模控制和辅助反馈控制分析两个子模块。相较于现有的控制策略，本文所提控制策略能够有效调节系统容错控制能力。

1 水电机组调节系统模型描述

水轮机调节系统是一个水力、机械以及电气多物理场强耦合非线性系统。本文重点研究水轮发电机组及其输水流道的动态过程，因此在建模过程中，将负荷在系统中的作用以负荷自调节系数的方式加以简化。水轮机调节系统的被控对象可如图1所示。

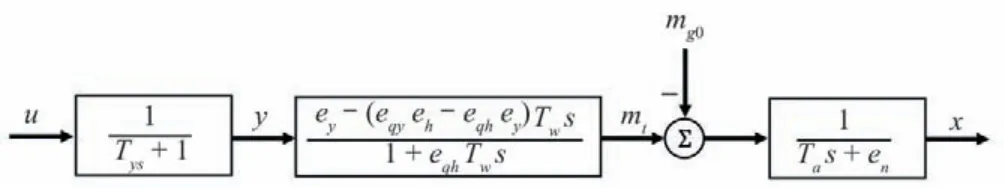
图1 调节系统被控对象框图Fig.1 Turbine regulation system control block diagram

1.1 接力器数学模型

控制器给出的控制律，接力器对控制信号进行放大和变换，以获得足够的功率来驱动水轮机导叶，其数学模型Gg(s)可以表示为：

式中：Ty为水轮发电机接力器时间常数。

1.2 水轮机数学模型

根据文献［1］，水轮机及其有压引水系统的刚性水击传递函数Gt(s)为：

式中：Tw为引水系统的水流惯性时间常数；ey为水轮机主动力矩与其导叶开度之间的传递系数；ex为水轮机力矩与其转速之间的传递系数；eh为水轮机力矩与其水头之间的传递系数；eqy为水轮机流量与其导叶开度之间的传递系数；eqx为水轮机流量与其转速之间的传递系数；eqh为水轮机流量与其之间水头传递系数。

1.3 发电机数学模型

发电机模型采用传递函数型发电机负荷动态方程，其数学表达式可描述为：

式中：Ta为水轮发电机惯性时间常数；xe为机组转速偏差；en为发电机（负荷）力矩对转速传递系数；mg0(s)表示外负荷对调节系统的扰动。

1.4 调节系统数学模型

在不考虑负载扰动的状态下，该水轮机调节系统状态空间模型可以描述为：

其中状态矩阵A与B，系统输出矩阵C与D，以及状态向量x(t)定义如下：

式中：y表示主接力器行程相对值；h表示蜗壳水压相对值；u表示控制输入。

参考文献［12］的思想，对水轮机调节系统输出变量xe后添加一积分环节，即xi=Ki∫xedt（Ki为积分系数），以消除机组转速稳态误差。那么，含积分环节的水轮机调节系统动态状态方程可表示为：

其中：

2 容错滑模控制器设计

水电机组调节系统频繁调节会导致其出现不同程度的老化。在这种非极端故障出现的情况下，调节系统表现出控制信号的调节不足，即控制器的输出信号存在不确定与干扰。在式（5）所描述的理想调节系统数学模型基础上，此时系统用状态空间微分方程可描述为：

其中：不确定与干扰项|Θ(x，t)|≤δf；δf为系统反映出的控制故障上限。

针对式（6）所描述的考虑调节系统不确定性与干扰的模型，本文结合基于等效的滑模控制理论和基于辅助反馈的滑模控制分析，设计水电机组调节系统的滑模容错控制律。

2.1 基于等效的滑模控制理论

定义与状态相关的滑模面S(t)如式（7）所示：

其中，矩阵P为一个正定矩阵；通过矩阵P的合理设计实现S(t) →0。

对于水电机组调节系统，本文所设计的容错滑模控制器的数学表达式可描述为：

根据滑模控制理论中的等效原理，取此时的控制不确定与干扰函数Θ(x，t)为0。由式（5）描述的调节系统线性系统的理想数学模型，可以推导出：

进而，可得到容错滑模控制器的等效控制律ueq(t)部分的数学表达式为：

其中，ε0＞0；sgn(*)为符号函数。

选取Lyapunov函数为：

其中的S(t)的导数有以下推导结果：

因此，可以推导求得Lyapunov函数V(t)的导数为：

根据，Lyapunov 稳定性定理，当(S) ≤-ε0|S(t)|时，当t→∞，可以使得S(t) →0；但是，由于式（7）中对于S(t)的定义，当式（11）的一阶导数满足(S) ≤-ε0|S(t)|并不能保证水电机组调节系统中的状态x(t) →0。对此，需要进一步详细分析。

采用线性矩阵不等式来设计的正定矩阵P，为了求解控制律当中的矩阵P，参考文献［13］，将文本所设计的控制律（8）改成为：

其中，v(t) =Kx(t) +ueq(t) +un(t)。

代入式（14）所描述的控制律，此时水电机组调节系统的数学描述为：

其中，=A′-B′K，通过设计K使得为Hurwitz 矩阵（多项式的所有根都有负实部），这样可以确保闭环系统渐近稳定。

通过这个矩阵P的设计可以有效地调节x的收敛过程，并有利于线性矩阵不等式的求解。定义Lyapunov函数V(t)为：

对式（15）求一阶导数可以得到：

其中，Q1=P(A′+B′K)；Q=QT1+Q1。

为了能够实现x指数收敛，即Lyapunov 函数V(t)的导数能够满足：

可以定义如下的式子：

取式（17）中的αP+Q＜0，α＞0，能够满足：

由此可以解得：

如果t→∞，那么V(t) →0，从而有x→0 是以指数收敛的。

线性矩阵不等式（17）中，矩阵Q中包含有矩阵P和矩阵K，那么通过公式（17）中的Q进行展开可以得到：

对式（20）左右同乘P-1，那么可以得到：

令F=KP-1以及N=P-1，则P-1KT=FT，由式（21）可以得到一个线性矩阵不等式为：

根据P的定义，可以设计另一个线性矩阵不等式为：

通过联立式（22）和（23），并且设置合适的指数大小α数值，就可以求得有效的反馈矩阵K。

4 仿真试验验证

基于MATLAB/Simulink 仿真环境，搭建了如图1 所示的混流式机组调节系统模型，从而验证所提控制器的有效性。并选取机组实际运行工况进行仿真，机组相关仿真参数如表1所示。其中，接力器时间常数Ty= 0.2，机组惯性时间常数Ta= 9.06。

表1 机组运行参数Tab.1 Operating parameters of the unit

为了通过对比突出所提控制策略的优异性能，使用文献［14］中的智能优化算法设计的 PID 控制器最佳参数为Kp= 10，Ki= 0.6，Kd= 0.02；最佳PI 控制器参数为Kp= 20，Ki= 0.663 2。采用的滑模容错控制器如式（8）所示，定义δf= 0.3，ε0= 0.15，α= 3。并采用饱和函数sat(*)代替切换函数sgn(*)，sat(*)中的边界层厚度为Δ= 0.05。

机组所在某个工况的运行参数如表1 所示。根据这些参数，联立矩阵A′与矩阵B′，并结合式（22）和（23）。利用MATLAB 中的线性矩阵不等式求解工具箱（LMI Toolbox）［13］。经求解可得到矩阵F和P的具体数值。

那么，状态反馈矩阵K由K=FP可以解得：

4.1 仿 真

本节仿真水电机组处于表1 参数所描述的工况。同时，考虑引入控制的不确定性与干扰大小为：Θ(t) = 0.3sint，该函数用于描述系统时间变化的随机故障。

机组甩75%负荷扰动后的响应曲线如图2 所示。从图2 中可以看出，对于机组甩75%负荷扰动，PI、PID、滑模容错控制（SMC）都可以稳定下来。但是，由于引入了控制不确定性与扰动，PI与PID控制并不能很好地使得系统完全稳定下来。此外，PID 与PI 控制下的机组在该工况下蜗壳水压相对值升上值较大，而SMC 控制下的机组能够维持机组的蜗壳水压相对值值保持在合适的范围内。

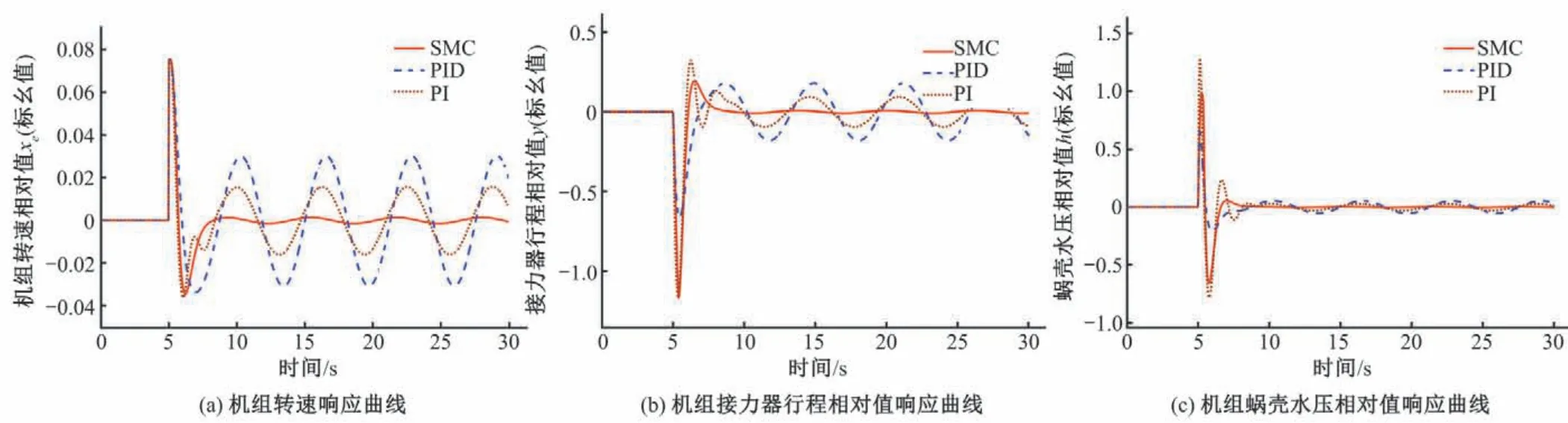
图2 甩75%负荷扰动仿真响应曲线Fig.2 Simulation response curve of 75% load dumping disturbance

如图3 所示，该图仿真了机组增加10%负荷时系统的响应曲线。从该图3（a）可以发现，滑模容错控制下的机组转速响应稳定较为迅速，能够在不到5 s 时间内达到基本稳定状态。同时，从图3 中可以发现，由于引入了控制的不确定性与干扰，传统的最优PID 与PI 控制无法做到有效的调节，此时机组接力器行程以及蜗壳水压相对值出现了反复的振荡，这对机组的安全与稳定性带来极大的危险。而滑模容错控制作用下的机组能够使得这部分振荡量维持在极小的范围内。

图3 增加10%负荷扰动仿真响应曲线Fig.3 Simulation response curve of 10% load increase perturbation

5 结 论

本文针对的水轮机调节系统中的控制不确定与干扰，提出了一种基于线性矩阵不等式的状态反馈滑模容错控制器。该控制器利用等效滑模以及辅助反馈滑模控制分析设计。并分别基于线性矩阵不等式和Lyapunov 稳定性实现了控制律调整和闭环系统的稳定性证明。结果表明，在考虑控制不确定性与干扰时， 所提控制方法能够有效提高机组稳定性，并且减少机组蜗壳水压波动，该方法对于提高机组运行稳定与安全具有重要意义。